Effective image segmentation on graphs

Image segmentation and edge detection ( edge detection ) play an important role in Computer Vision systems and are used for scene recognition and selection (definition) of objects. By and large, this is the same tool as, for example, sorting, designed to solve higher-level tasks. And therefore, understanding the design of this class of algorithms will not be superfluous when building such systems, taking into account the requirements (in terms of quality / performance) and the specifics of the tasks.

This paper briefly describes the algorithm «Efficient Graph-Based Image Segmentation» authors Pedro F. Felzenszwalb ( MIT ) and Daniel P. Huttenlocher( Cornell University ), published in 2004. Yes, the algorithm is relatively old, but despite this, it is still very popular, showing good results in terms of performance.

Under the cut - a large mixture of pictures and text, not demanding on the current level of knowledge of the subject. Curiosity is welcome .



First, an algorithm will be described on graphs, at first glance, having little to do with image processing. However, a little later its interpretation will be given in relation to image segmentation.

Kraskal Algorithm

The Kraskal algorithm ( wiki ) builds a wireframe - the minimum spanning tree of a given graph. Next, the English abbreviation MST (minimum spanning tree) will be used .

Objective: several settlements are located on the map (several contacts are located on the board), it is necessary to connect all of them to each other so that the total length of roads (wires) is minimal.


* Yes, the task in such a formulation is usually called the “Steiner problem” ( article ), having solved which, cities can be connected even cheaper. But we, in the end, do not pave the asphalt ... =)

For the solution we need:

• Graphs : Briefly about what it is and how they are represented in the code has already been stated on Habré ( article )
• Kraskal's algorithm ( wiki ): the main "engine" for solving the problem in this formulation. It is very well described in Cormen, Lazerson’s Bible Algorithms: Construction and Analysis ( book )
• Disjoint-set data structure ( wiki ): An additional structure necessary for the efficient execution of the above algorithm. How it is arranged is described in the same bible, but only under a slightly different name ( if memory serves: Union Find-Set, something like that )

In the current statement of the problem, the vertices of the graph (v _i ) are cities, and the edges e (v _i , v _j ) are roads between cities. We know the distances between pairs of cities (v _i , v _j ) - this is the weight of the edges w (e (vi, vj)). You need to find MST, i.e. such a tree in the graph (without cycles: why build extra roads) so that the sum of the edges is minimal and at the same time all the vertices are reachable.

Initially, each peak (city) in itself is the only proud representative of the corresponding set G ₁ , G ₂ , ... G _N(by the number of vertices). Let while thinks that she formed MST. During the algorithm, we efficiently and diplomatically combine all these disparate sets into a single G so that the vertices involved in it form MST. For this:

• We sort all the edges in the graph in order of increasing length (road)
• Running along the ribs in increasing order of lengths, we look at the ends of the ribs e = (a, b):
  • If the vertices (a and b) belong to the same set : So, they already participate in some formed subset of micro-MST, inside their subgraph the sum of the edges is already minimal. Such an edge is skipped - we do not need it because otherwise, it forms a cycle in a tree, and we will waste asphalt
  • If the vertices (a and b) belong to different subsets of micro-MST: You need to combine, because we found an edge (road) of minimum length, combining (merging) both subsets into one. All ribs of shorter length have already been considered and it is not possible to combine them more cheaply than this rib. Such an edge is recorded in the list of edges used to construct the MST tree, and the sets are combined into one
  • We continue the union cycle until we get one single set equal to the desired MST, in which all vertices of the graph will be present
• We get one single set of vertices (MST) and a list of edges used to combine it, which is a tree of minimum total length that combines all the vertices.

Disjoint-set data structure

To implement the concept of "set" in the Kraskal algorithm, a Disjoint-set data structure is used . Work with it is optimized to perform two basic operations:

• Find out for some vertex which set it currently belongs to
• Quickly combine these sets into one

To get closer to the topic of image segmentation, we continue the description in terms of image pixels and their colors. Suppose we are segmenting a budgie against the backdrop of some Japanese blue sea. First, each pixel (the top of the graph) will be on its own - in its own segment (set), but during the algorithm, the pixels (vertices) of a “similar” color (one object) are gradually combined into one segment.

Suppose, at a certain step of the algorithm, an edge is connected that connects two adjacent pixels: at one end of the edge, the pixel is “orange”, and at the other “red”. The edge length is defined as the “color difference” between the pixels. All the ribs of shorter length (with a similar color) are already combined: the orange and red segments of the budgie have probably already been highlighted. Following the algorithm, we need to find out if the current “orange” and “red” pixels are in the same segment? If they are different, and we believe that the segments are similar in color, then we combine them into one and continue building ... In general, the same Kraskal algorithm, only with pixels.

The structure used for these operations is very similar to a tree (although it is implemented by an array of indices). In it, for each pixel, the ancestor is indicated, i.e. a pointer (index) to some similarly colored pixel located in the same segment. Basic operations:

• Search for a segment of some pixel 'x': we go along the ancestors to the very top. The topmost pixel is the root of the tree, the "representative" of this segment at the moment.
• The union of segments . If the pixels have different “representatives”, then they belong to different segments, otherwise there would be one root. To unite them, the “representative” of a segment of a lower height (from the farthest pixel to the root) is referenced (from it we point out) to the longer “representative” so as not to increase the height of the tree. Now we have a combined segment with a common representative.
• In order not to run far from the pixel to the root the next time, after the “representative” has been successfully detected, we establish a direct link from the pixel - immediately to it. This shortens the path of the next searches, and is called " path compression ".

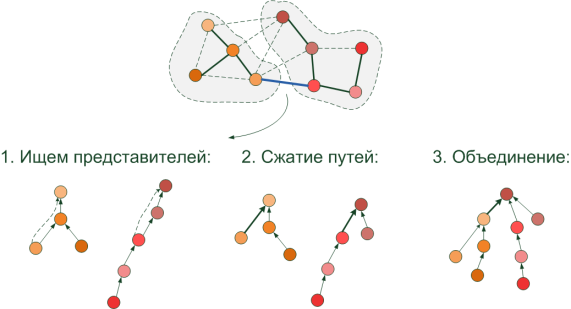
Well, now we can efficiently search for segments by pixels and combine them, as well as build MST using the Kraskal algorithm. It's time to find out how the decision is made to join or separate the two areas.

Divide and rule

The segmentation algorithm should clearly determine where one segment ends and another begins. As a rule, borders are characteristic differences in brightness and / or color shades found in areas of object-background, plane-shadow, parrot-sea, inscription on the fence ... And if the “difference” is greater than a certain “threshold” (threshold), then this should follow that these are different segments. But there is a small problem: the differences can vary greatly for different objects, and it is difficult to “separate” the segments with an uniquely defined (const) threshold value (threshold). For the table surface against the wall: the differences between adjacent pixels along the table surface (wall) will be relatively small, but at the table-wall border there will be a jump that will separate the segments. It is clear. And if we have a parrot on the background of the sea? He himself is very "motley", inside it, large differences in intensity (green-red-yellow- ...) in order to "separate" it from the sea, you need another "threshold" (threshold). And gradually we come to the conclusion that the threshold that decides that neighboring segments are “not destined to be together” should be based not only on local indicators: the intensity difference along one edge (connecting adjacent pixels), but also on how much these segments themselves themselves smooth (in terms of color) or "colorful".

Gray pictures

Before proceeding to the processing of full-color pictures, consider a simplified version when the image is represented by shades of gray ( grayscale ), ie in each cell of the image matrix, a number is stored in the interval [0 ... 1], which represents the brightness of the pixel.

Efficient Graph-Based Image Segmentation

Each image pixel is represented by a vertex in the graph. And the weight (length) of the edge connecting the neighboring vertices is expressed by the formula: w (v _i , v _j ) = | I (p _i ) -I (p _j ) | where I (p _i ) is the intensity (brightness) of the pixel p _i

During the execution of the Kraskal algorithm, at the intermediate stage we will have several disparate segments (subsets of pixels), with a minimum total weight of edges inside: the segments will be joined by edges of minimum length, i.e. with minimal "intensity differences" between adjacent pixels. Therefore, neighboring pixels within the same segment will be similar in color. But only up to a certain value of the maximum edge (intensity difference) ...

And so ... we took the minimum edge at the current step. For two pixels that are adjacent vertices of this edge, we determine from one (already constructed) segment?

• Yes , from one segment: we just continue the execution of the algorithm.
• No . It is necessary to determine whether the segments represent parts of the same object in the image and should they be combined, or are their intensities “significantly” different?

To determine the difference between the segments, we associate with each segment already constructed a certain value - the maximum intensity difference inside it, i.e. The longest edge in MST inside a segment:

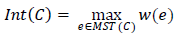
You won’t have to search for it separately - just save the length of the edge added when combining the components of the “sub-segments”. Indeed, at the time of the merger, the length of the added edge was longer than in the already built MST of each “subsegment”, because edges are processed in ascending order.

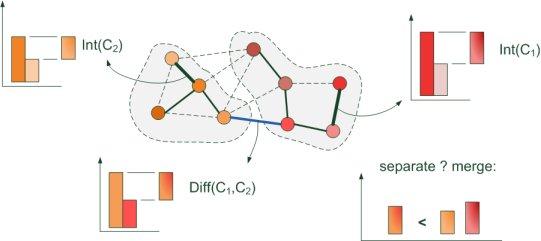
We get an approximate decision rule for segments C ₁ , C ₂ :

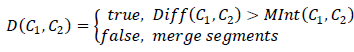
	Symptom: Should these segments be distinguished?
	The current edge of minimum length connecting two disparate segments
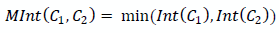	Smaller (from large) intensity difference inside one of the considered segments

It turns out that in order for the segments to “merge”, the difference in intensities at their boundary should be less than the maximum difference inside each of the combined segments:

I am looking for you

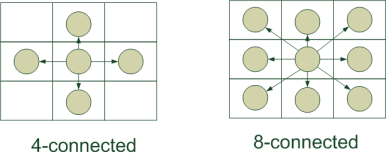
How to build a graph from the image? Which pixels are adjacent? On the surface are two main approaches:

• 4-connected : each pixel is connected to the neighboring ones from the top / bottom / left / right. Such a construction is attractive in that the number of edges in the graph is minimal.
• 8-connected : in addition to the previous version, we connect each pixel to neighboring ones located diagonally. Thus, there are more edges in the graph; the algorithm runs somewhat slower. But the resulting segmentation should be better - because more relationships between pixels are taken into account.

The algorithm should give better results on the 8-connected graph, but 4-connected gives very acceptable results and at the same time runs much faster. And as the “distance” for processing color images, we can take just such a simple pixel color difference, as implemented by the authors of the algorithm:

However, such a distance formulation has a drawback. If we consider the "intensity difference" between locally neighboring pixels, then the sky in the next picture will be divided into 2 separate segments running across the wire, or we will get an even worse result if we process the lawn against the background of the grid:


Each fragment of the lawn will be marked as a separate segment, but this is one object!

Therefore, in an alternative embodiment, the authors propose to consider not only nearby pixels, but starting from the local properties of the image (pixels located in the immediate vicinity), try to "jump over the wire" (see picture) and reach for the continuation of the segment located at some distance. To do this, they suggest choosing the Euclidean distance as the edge length, depending both on the position of the pixels (x, y) and on their color (r, g, b):

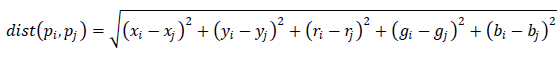
Now pixels will be considered “neighbors” if they are located nearby, or have a similar hue, although they may physically be at some distance. To build a graph, the authors propose connecting each pixel with 10 (20, 30) “closest”. This gives better segmentation, but requires more computing resources.

Stick together, team!

Returning to the very beginning. Once upon a time, when all the pixels were fragmented, a significant difference in intensities could be observed between the neighboring ones, preventing them from merging. It is unlikely that we were given a microscopic photograph where each pixel needs to be isolated - most likely, they are part of some larger object (a parrot). So that they succumb to the “merge” (merge) to a greater extent than already constructed large segments, for which the correctness of the partition is more important, add a value depending on the size of the constructed segment in the decisive rule:, where | C | Is the power of the segment in question (the number of pixels in it at the current moment), and k- This is already a segmentation parameter set manually. With a similar amendment in the decision rule, the formula will be used: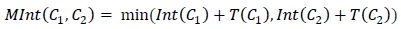


The “correction” is gradually leveled with the growth of the segment (increase | C | ) ...

In fact, instead of such a task T, you can choose another function that takes into account the specifics of the processed images: the shape of the segments, the position in the photo, certain color shades ...

Gaussian blur

Returning to very "motley" pictures:


It is clear that when determining the distance between pixels in such a definition as "intensity difference", the pixels of a "motley", even a single object, will not be very pliable to be combined into one object. To make them more “accommodating” to combining and remove noise / artifacts, a Gaussian filter (http://habrahabr.ru/blogs/webdev/43895/) with a certain radius (standard deviation) sigma is usually applied to the image . This causes “interpenetration” of the color components of the pixels, and they are more willing to make contact.

Total

There are many methods for segmentation: various approaches are very well described in the article - “Image Segmentation Methods: Automatic Segmentation”. And by and large, segmentation should be either high-quality or productive, and if you are lucky, then all at once. The method described above is just a productive option.

In this method of segmentation, the most time-consuming process is sorting all the edges, performed for O (e log ⁡e), where e is the number of edges in the graph. Thus, for an NxM image, the pixel edges will be: | e | = 4 * N * M

The source code of the algorithm is available at this link .

But what about OpenCV?

Everybody’s favorite OpenCV library ( wiki ) has a “ cvPyrSegmentation ” method , i.e. pyramidal image segmentation method. It is arranged somewhat differently. His description would take another article, therefore - a picture. Segments are built in layers (level), combining similarly colored pixels into one (located above the layer), and then sequentially processing layers located at the next level (level) above “to the stop”:


In 2006, in the Univesity of Malaga (Spain), several pyramidal algorithms were compared and the results are presented in the following article :


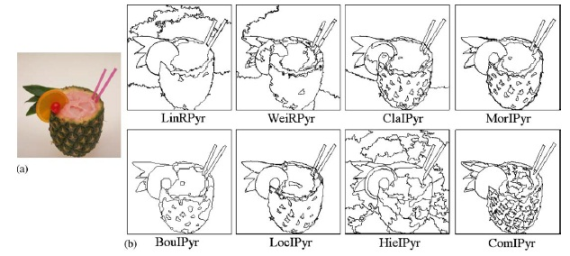
The authors came to the conclusion that out of 8 methods, 3 are worthy of attention, due to which fairly high-quality results are obtained for splitting the image into objects. However, it is worth noting that the execution time of the pyramidal algorithms ranges from 0.5 seconds. up to 4.5 sec. (256x256 pixels at Pentium 766 MHz), while the considered " Efficient Graph-Based Image Segmentation " is performed according to the authors of "in fraction of a second". At us, 1024x768 the photo worked out in 0.5 seconds (U9400 2 x 1.4GHz) inside the "nesting doll": VMWare - Matlab - mex (C ++). In general, pyramidal - quality, the graphs described in the article - speed. Both have the right to life. =)


To the most diligent readers, we will reveal the secret of “magic bubbles”: what kind of numbers are shown in the pictures? These are just the parameters of the " segmentation (sigma, k, min) " method , 2 of which you are already familiar with, and the 3rd " min " is the forced minimum segment size so that there are no "small" ones.


Good luck

PS I ask you not to kick much, this is my ninth post on Habré.