Sports interview
Recently I was interviewed in a reputable company. Gave several dozen logical tasks. He coped without much difficulty, but time was running out. The inspector looked at me with a grin: "You have not done a simple task." Honestly, I felt uneasy.
And here is the task:

It seems to be a classic task from the problem book of class 7-9. Further better to read, if there is an answer.
I answered intuitively, without thinking much, it was just a minute - “Vasya”. Perhaps you have the opposite answer.
I ran on sprint distances and intuitively understood that it is unreal to play 10 meters. I knew the kinematics of the 100-meter race, which was the lifeline. I did not agree with this decision. I asked for 10 minutes so that I could substantiate my answer. “Well, come on,” I heard.
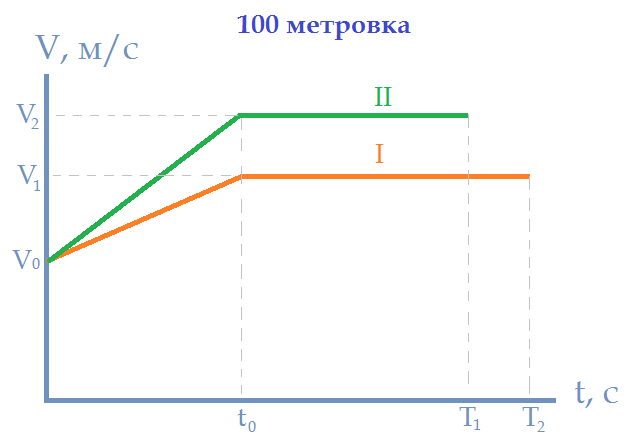
The condition of the task says nothing about the nature of the movement. Accordingly, the nature of the movement we take the closest to the real. Below is a speed chart as you go the distance.

For simplicity, take a simplified model. We will assume that up to the moment t0 the athletes gain speed linearly, and then, the speed is constant. Also, both athletes have the same initial speed and acceleration time.
Now we fix a series of variables to solve the problem numerically. We immediately take ranges to consider different categories of athletes:
This is enough to solve the problem completely. Go.
From the first race we get the connection of the maximum speeds of the athletes (I) and the time T1 and T2, during which the athletes run 100 meters (II - III):
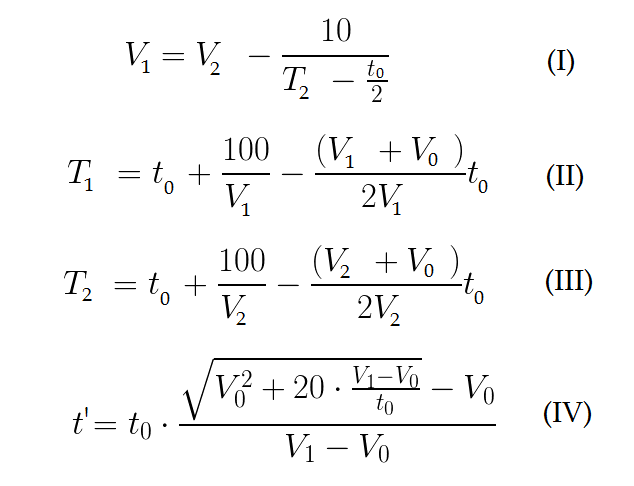
In the second run, T1 and T2 will be the same (by condition), but the second athlete will start with a delay t `. Thus, if T1 - T2> t`, then the second athlete (Sasha) will win again. t` is the time during which Vasya will run the first 10 meters (IV).
Well, we substitute various combinations of initial parameters and look at the result (T, c - Sasha’s lag at the finish in seconds, X, m - lag in meters):

The table is sorted by time lag. As we see, in all the cases we have considered, Sasha resorts second. There are even cases where the initial handicap of 10 m increases. Thus, in our model, which is as close to real as possible, Sasha has a microscopic probability of winning. The “constant speed” model is a good simplification in many problems, but here it is the case when this leads us to the opposite result.
In conclusion, I will say that the answer is not the most important thing. What is important is an adequate model and course of your thoughts.
PS For such a “wrong” solved problem, I received a big fat plus.
And here is the task:
Sasha and Vasya are running 100 meters. When Sasha finishes, Vasya runs only 90 meters.
In the second run, they also run, only Sasha starts when Vasya runs the first 10 meters.
Who will finish first?

It seems to be a classic task from the problem book of class 7-9. Further better to read, if there is an answer.
I answered intuitively, without thinking much, it was just a minute - “Vasya”. Perhaps you have the opposite answer.
Vasya and Sasha will be at the mark of 90 meters at the same time (follows from the first race + taking into account the odds of 10 meters). And the remaining 10 meters ... - Sasha is faster- that's the whole answer. A beautiful decision, isn't it ?! I did not think of it before.
I ran on sprint distances and intuitively understood that it is unreal to play 10 meters. I knew the kinematics of the 100-meter race, which was the lifeline. I did not agree with this decision. I asked for 10 minutes so that I could substantiate my answer. “Well, come on,” I heard.
The condition of the task says nothing about the nature of the movement. Accordingly, the nature of the movement we take the closest to the real. Below is a speed chart as you go the distance.

For simplicity, take a simplified model. We will assume that up to the moment t0 the athletes gain speed linearly, and then, the speed is constant. Also, both athletes have the same initial speed and acceleration time.

Now we fix a series of variables to solve the problem numerically. We immediately take ranges to consider different categories of athletes:
- The instantaneous initial velocity V0, we take from 3-5 m / s, where 3 m / s - students, 4 - pro, 5 - champions;
- Acceleration time t0, at world championships it is ~ 5 s, students have less. Take a range from 3 to 5 seconds;
- The maximum speed V2, take 8 - 10 m / s, where 10 m / s - the level of the World Cup.
This is enough to solve the problem completely. Go.
From the first race we get the connection of the maximum speeds of the athletes (I) and the time T1 and T2, during which the athletes run 100 meters (II - III):
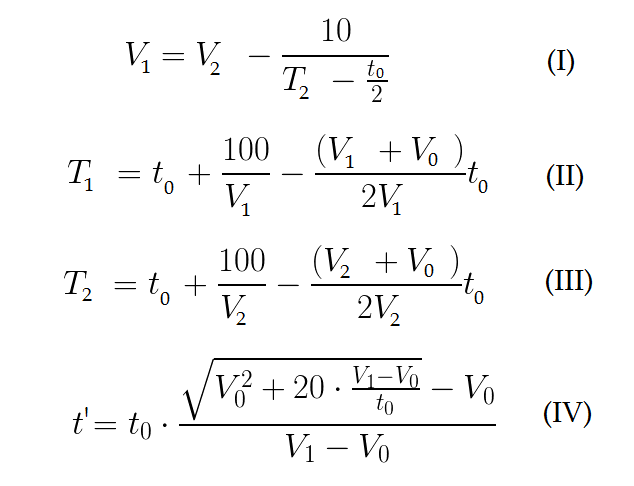
In the second run, T1 and T2 will be the same (by condition), but the second athlete will start with a delay t `. Thus, if T1 - T2> t`, then the second athlete (Sasha) will win again. t` is the time during which Vasya will run the first 10 meters (IV).
Well, we substitute various combinations of initial parameters and look at the result (T, c - Sasha’s lag at the finish in seconds, X, m - lag in meters):

The table is sorted by time lag. As we see, in all the cases we have considered, Sasha resorts second. There are even cases where the initial handicap of 10 m increases. Thus, in our model, which is as close to real as possible, Sasha has a microscopic probability of winning. The “constant speed” model is a good simplification in many problems, but here it is the case when this leads us to the opposite result.
In conclusion, I will say that the answer is not the most important thing. What is important is an adequate model and course of your thoughts.
PS For such a “wrong” solved problem, I received a big fat plus.
