Leaf math: how one unusual bush changed the equation of a plant growth model
- Transfer
We love leaves for their shade, autumn colors, smell, and the location of the leaves of the plant is a practical way to determine their species. However, the details of how plants control the location of their leaves remained an inexplicable mystery in botany. One species of Japanese plant with an unusual pattern of leaf arrangement has recently allowed us to take an unexpected look at how almost all plants control this arrangement.
“We have developed a new model to explain one particular pattern of leaf arrangement (phyllotaxis). But in fact, it reflects much more accurately not only the nature of this particular plant, but also the wide variety of almost all the patterns of leaf arrangement observed in nature, ”says Munetaka Sugiyama, associate professor at the Koisikawa Botanical Garden of Tokyo University.
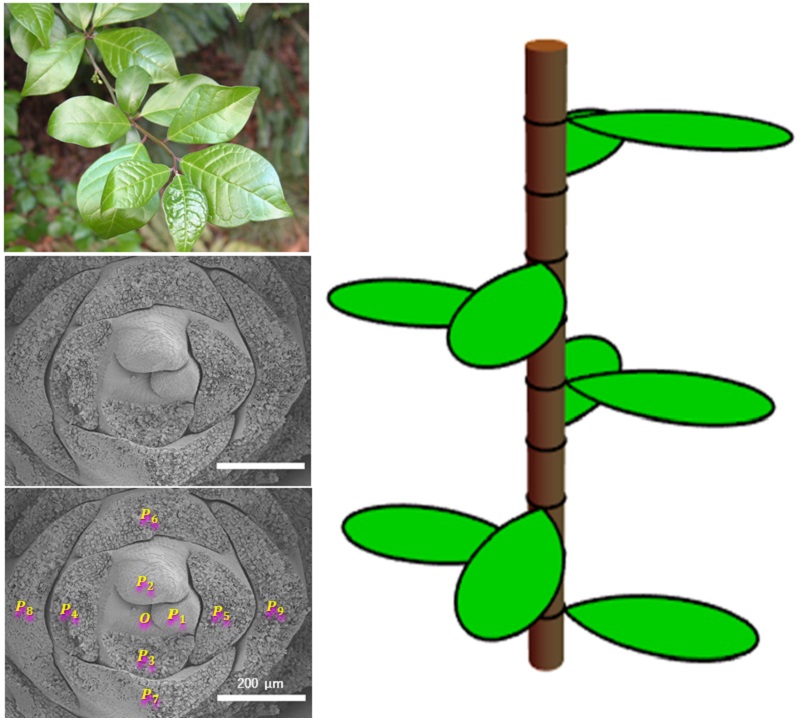
Leaves on a branch of O. japonica (top left) and a schematic representation of phyllotaxis orixate (right). The orixate pattern shows an unusual cycle of changing leaf angles, consisting of four values (from 180 degrees to 90 degrees, then to 180 degrees and to 270 degrees). The image from a scanning electron microscope (in the center and lower left) shows the winter bud Orixa japonica, in which the leaves begin to grow. The rudiments of leaves are sequentially labeled from the oldest leaf (P8) to the youngest (P1). Point O marks the tip of the shoot.
To determine the placement of leaves, botanists measure the angles between the leaves, moving along the stem from the oldest to the youngest leaf.
Standard patterns are symmetrical, in which leaves are arranged at regular intervals of 90 degrees (basil or mint), 180 degrees (stem herbs, such as bamboo), or Fibonacci spirals with golden corners (for example, needles of some spherical cacti or scarlet multi-leafed succulent).
An unusual pattern studied by the research team of associate professor Sugiyama is named "orixate" in honor of Orixa japonica , a shrub native to Japan, China and the Korean Peninsula. Sometimes O. japonica is used as a hedge.
The angles between the leaves of O. Japonica are 180 degrees, 90 degrees, 180 degrees, 270 degrees, and then the next sheet “resets” the pattern back to 180 degrees.
“Our study provides the potential to fully understand the amazing patterns of nature,” says Sugiyama.
Sugiyama's research team began its study with an exhaustive test of the mathematical equation used to model leaf placement.
Mathematically, the arrangement of leaves has been modeled since 1996 using an equation known as DC2 (Douady and Couder 2). The equation can generate many, but not all, patterns of leaf distribution observed in nature due to a change in various variables of the plant physiology, such as the relationship between different organs of the plant or the strength of chemical signals within the plant.
DC2 has two drawbacks that the researchers wanted to eliminate:
1) Whatever values are substituted into the DC2 equation, some rare location patterns cannot be calculated.
2) The pattern of the arrangement of leaves in a Fibonacci spiral (golden spiral) is the most common spiral pattern observed in nature, but it is only slightly more common than other spiral patterns calculated by the DC2 equation.

Orixate phyllotaxis simulation according to Expanded Douady and Couder 2. Video by Takaaki Yonekura, CC-BY-ND, originally published in PLOS Computational Biology DOI: 10.1371 / journal.pcbi.1007044
At least four unrelated plant species have an unusual orixate leaf arrangement pattern. Researchers suspect that there should be the possibility of creating an orixate pattern using the fundamental genetic and cellular mechanics common to all plants, because the opposite possibility of an individual evolutionary change, four or more times leading to the same, very unusual pattern, seems too unbelievable.
Equation DC2 uses one fundamental assumption that leaves emit a constant signal to suppress the growth of other leaves near them, and as the distance increases, this signal becomes weaker. Researchers suspect that this signal is most likely due to the plant hormone auxin, but the specific physiology is still unknown.
“We abandoned this fundamental assumption, suggesting that the power of suppression is not really constant, but changes with age. We tested both increase and decrease in strength with increasing age, and noticed that the unusual orixate pattern is calculated when old leaves have a stronger overwhelming effect, ”Sugiyama reports.
This conjecture that the strength of the inhibitory signal changes with age can be used for direct further research on the genetics or physiology of plant development.
Researchers call this new version of the equation EDC2 (Expanded Douady and Couder 2).
The first author of the research article, graduate student Takaaki Yonekura, developed computer simulations to generate thousands of leaf placement patterns calculated by the EDC2 equation, as well as to calculate the frequency of generation of identical patterns. The more common patterns in nature were calculated more often by EDC2, further reinforcing the accuracy of the ideas used to create the formula.
“There are other very unusual patterns of leaf arrangement that are still not explained by our new formula. Now we are trying to create a new concept that will be able to explain all the known patterns of leaf arrangement, and not almost all , ”Sugiyama said.
Each of the videos below shows a top view of the patterns of leaf arrangement when new leaves (red semicircles) form from the top of the shoot (black circle in the center) and grow outward. The suppression field is presented in the form of a contour map on which the highest suppression force is indicated in red, and the lowest is indicated in blue.

Simulation of the opposite (double-sided, distichous) phyllotaxis by the equation Expanded Douady and Couder 2. Video by Takaaki Yonekura, CC-BY-ND

Golden spiral phyllotaxis simulation using the Expanded Douady and Couder 2 equation. Takaaki Yonekura video, CC-BY-ND

Simulation of decussate phyllotaxis using the Expanded Douady and Couder 2 equation. Takaaki Yonekura video, CC-BY-ND

Expanded Douady and Couder 2 tricussate phyllotaxis simulation. Video by Takaaki Yonekura, CC-BY-ND
To determine the pattern of leaf arrangement (phyllotaxis), experts recommend studying a group of relatively new leaves. (In ancient Greek, phyllon (phyllon) means “leaf.”) Older leaves can change their direction (due to wind or exposure to the sun), which may complicate the determination of their true angle of attachment to the stem.
Imagine the stem as a circle and begin to carefully observe where the oldest and next oldest leaves are attached to the circle. The angle between these two leaves will be the first "angle of divergence." Continue to record the angles of discrepancy between ever younger leaves on the stem. The divergence angle pattern is a pattern of leaf arrangement.
The most common leaf arrangement patterns are opposite (regular with an angle of 180 degrees, bamboo), Fibonacci spiral (regular with an angle of 137.5 degrees, succulent Graptopetalum paraguayense ), cross-pair (regular with an angle of 90 degrees, basil) and three-sided (regular with angle of 60 degrees, Nerium oleander ).
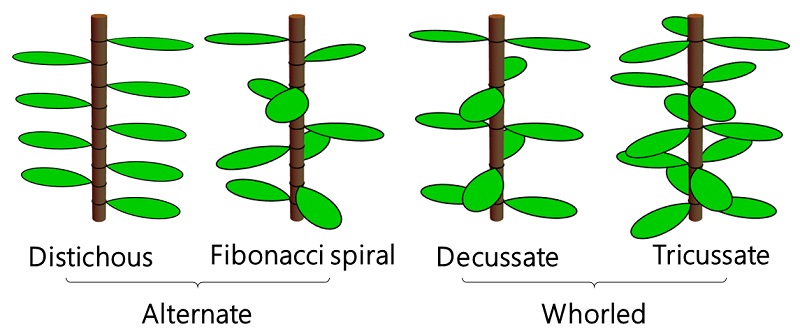
The arrangement of leaves with one leaf per node is called alternate phyllotaxis, and the arrangement of two or more leaves per node is called whorled. Common types of alternate phyllotaxis are distichous (bamboo) and spiral (aloe succulent multifolia), while common whorled species are decussate (basil and mint) and tripartite (tricussate) ( Nerium oleander ). Image of Takaaki Yonekura, CC-BY-ND
Takaaki Yonekura, Akitoshi Iwamoto, Hironori Fujita, Munetaka Sugiyama, “Mathematical model studies of the comprehensive generation of major and minor phyllotactic patterns in plants with a predominant focus on orixate phyllotaxis,” PLOS Computational Biology : June 6, 2019, doi: 10.1371 / journal.pcbi.1007044.
Link ( Publication )
“We have developed a new model to explain one particular pattern of leaf arrangement (phyllotaxis). But in fact, it reflects much more accurately not only the nature of this particular plant, but also the wide variety of almost all the patterns of leaf arrangement observed in nature, ”says Munetaka Sugiyama, associate professor at the Koisikawa Botanical Garden of Tokyo University.
It's all about the corners

Leaves on a branch of O. japonica (top left) and a schematic representation of phyllotaxis orixate (right). The orixate pattern shows an unusual cycle of changing leaf angles, consisting of four values (from 180 degrees to 90 degrees, then to 180 degrees and to 270 degrees). The image from a scanning electron microscope (in the center and lower left) shows the winter bud Orixa japonica, in which the leaves begin to grow. The rudiments of leaves are sequentially labeled from the oldest leaf (P8) to the youngest (P1). Point O marks the tip of the shoot.
To determine the placement of leaves, botanists measure the angles between the leaves, moving along the stem from the oldest to the youngest leaf.
Standard patterns are symmetrical, in which leaves are arranged at regular intervals of 90 degrees (basil or mint), 180 degrees (stem herbs, such as bamboo), or Fibonacci spirals with golden corners (for example, needles of some spherical cacti or scarlet multi-leafed succulent).
An unusual pattern studied by the research team of associate professor Sugiyama is named "orixate" in honor of Orixa japonica , a shrub native to Japan, China and the Korean Peninsula. Sometimes O. japonica is used as a hedge.
The angles between the leaves of O. Japonica are 180 degrees, 90 degrees, 180 degrees, 270 degrees, and then the next sheet “resets” the pattern back to 180 degrees.
“Our study provides the potential to fully understand the amazing patterns of nature,” says Sugiyama.
Plant math
Sugiyama's research team began its study with an exhaustive test of the mathematical equation used to model leaf placement.
Mathematically, the arrangement of leaves has been modeled since 1996 using an equation known as DC2 (Douady and Couder 2). The equation can generate many, but not all, patterns of leaf distribution observed in nature due to a change in various variables of the plant physiology, such as the relationship between different organs of the plant or the strength of chemical signals within the plant.
DC2 has two drawbacks that the researchers wanted to eliminate:
1) Whatever values are substituted into the DC2 equation, some rare location patterns cannot be calculated.
2) The pattern of the arrangement of leaves in a Fibonacci spiral (golden spiral) is the most common spiral pattern observed in nature, but it is only slightly more common than other spiral patterns calculated by the DC2 equation.
Unusual pattern

Orixate phyllotaxis simulation according to Expanded Douady and Couder 2. Video by Takaaki Yonekura, CC-BY-ND, originally published in PLOS Computational Biology DOI: 10.1371 / journal.pcbi.1007044
At least four unrelated plant species have an unusual orixate leaf arrangement pattern. Researchers suspect that there should be the possibility of creating an orixate pattern using the fundamental genetic and cellular mechanics common to all plants, because the opposite possibility of an individual evolutionary change, four or more times leading to the same, very unusual pattern, seems too unbelievable.
Equation DC2 uses one fundamental assumption that leaves emit a constant signal to suppress the growth of other leaves near them, and as the distance increases, this signal becomes weaker. Researchers suspect that this signal is most likely due to the plant hormone auxin, but the specific physiology is still unknown.
Rare patterns and standard rules
“We abandoned this fundamental assumption, suggesting that the power of suppression is not really constant, but changes with age. We tested both increase and decrease in strength with increasing age, and noticed that the unusual orixate pattern is calculated when old leaves have a stronger overwhelming effect, ”Sugiyama reports.
This conjecture that the strength of the inhibitory signal changes with age can be used for direct further research on the genetics or physiology of plant development.
Researchers call this new version of the equation EDC2 (Expanded Douady and Couder 2).
The first author of the research article, graduate student Takaaki Yonekura, developed computer simulations to generate thousands of leaf placement patterns calculated by the EDC2 equation, as well as to calculate the frequency of generation of identical patterns. The more common patterns in nature were calculated more often by EDC2, further reinforcing the accuracy of the ideas used to create the formula.
“There are other very unusual patterns of leaf arrangement that are still not explained by our new formula. Now we are trying to create a new concept that will be able to explain all the known patterns of leaf arrangement, and not almost all , ”Sugiyama said.
Each of the videos below shows a top view of the patterns of leaf arrangement when new leaves (red semicircles) form from the top of the shoot (black circle in the center) and grow outward. The suppression field is presented in the form of a contour map on which the highest suppression force is indicated in red, and the lowest is indicated in blue.

Simulation of the opposite (double-sided, distichous) phyllotaxis by the equation Expanded Douady and Couder 2. Video by Takaaki Yonekura, CC-BY-ND

Golden spiral phyllotaxis simulation using the Expanded Douady and Couder 2 equation. Takaaki Yonekura video, CC-BY-ND

Simulation of decussate phyllotaxis using the Expanded Douady and Couder 2 equation. Takaaki Yonekura video, CC-BY-ND

Expanded Douady and Couder 2 tricussate phyllotaxis simulation. Video by Takaaki Yonekura, CC-BY-ND
Do it yourself: identify the pattern
To determine the pattern of leaf arrangement (phyllotaxis), experts recommend studying a group of relatively new leaves. (In ancient Greek, phyllon (phyllon) means “leaf.”) Older leaves can change their direction (due to wind or exposure to the sun), which may complicate the determination of their true angle of attachment to the stem.
Imagine the stem as a circle and begin to carefully observe where the oldest and next oldest leaves are attached to the circle. The angle between these two leaves will be the first "angle of divergence." Continue to record the angles of discrepancy between ever younger leaves on the stem. The divergence angle pattern is a pattern of leaf arrangement.
The most common leaf arrangement patterns are opposite (regular with an angle of 180 degrees, bamboo), Fibonacci spiral (regular with an angle of 137.5 degrees, succulent Graptopetalum paraguayense ), cross-pair (regular with an angle of 90 degrees, basil) and three-sided (regular with angle of 60 degrees, Nerium oleander ).

The arrangement of leaves with one leaf per node is called alternate phyllotaxis, and the arrangement of two or more leaves per node is called whorled. Common types of alternate phyllotaxis are distichous (bamboo) and spiral (aloe succulent multifolia), while common whorled species are decussate (basil and mint) and tripartite (tricussate) ( Nerium oleander ). Image of Takaaki Yonekura, CC-BY-ND
Articles
Takaaki Yonekura, Akitoshi Iwamoto, Hironori Fujita, Munetaka Sugiyama, “Mathematical model studies of the comprehensive generation of major and minor phyllotactic patterns in plants with a predominant focus on orixate phyllotaxis,” PLOS Computational Biology : June 6, 2019, doi: 10.1371 / journal.pcbi.1007044.
Link ( Publication )
