Japanese Crossword Solution at Haskell
Japanese crossword puzzle is a puzzle in which, using a set of numbers, you need to recreate the original black and white image. Each row and each column of pixels has its own set, each number in which, in turn, corresponds to the length of a block of consecutive black pixels. There should be at least one white pixel between such blocks, but their exact number is not known. Magazines entirely devoted to these puzzles are in most newsstands, so I think almost all of them have met at least once, and therefore a more detailed description can be omitted here.
At some point, I wanted to “teach the computer” to solve Japanese crosswords as I myself solve them. No lofty goal, just for fun. Then methods were added that I myself can’t apply due to the limited capabilities of the human brain, but, in fairness, the program copes with all the crosswords from the magazines without them.
So, the task is simple: solve a crossword puzzle, and if there are many solutions, then find them all. The solution is written in Haskell, and although the code substantially complements the verbal description, even without knowledge of the language, the general essence can be understood. If you want to feel the result live, on the project page you can download the sources (I did not upload binary assemblies). Solutions are exported to Binary PBM, and you can extract conditions from it.
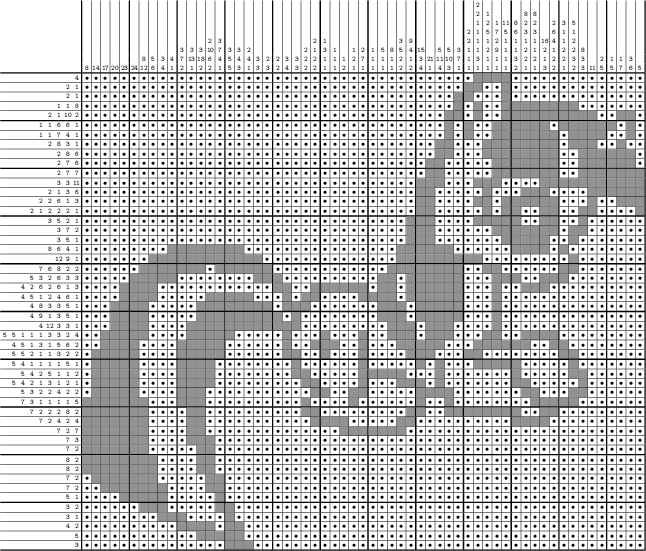
Despite the fact that I tried to write as clearly as possible, I did not fully succeed. Under the cut a lot of letters and code and almost no pictures.
At the heart of the whole program is your bike for a bit mask. It is not too fast, but it has a property that was important to me in the debugging process: it crashes during operations that do not make sense, namely during any operation on masks of different lengths. I will give here only the signatures of the functions and the picture explaining the principle of their work; the implementation is very primitive and has no direct relation to the solution.
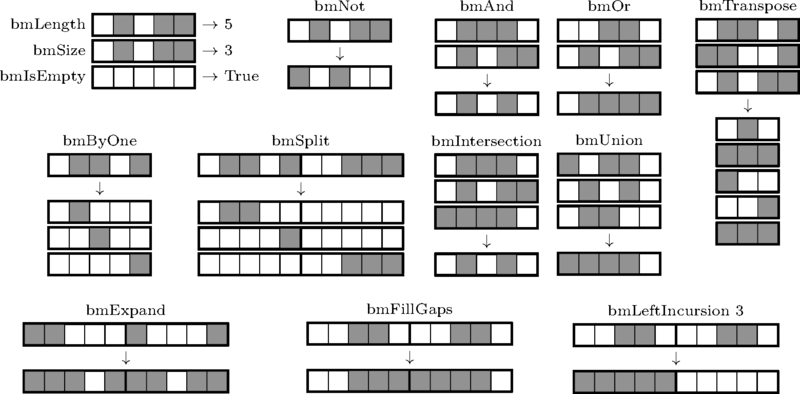
I think that this graphic description exhaustively for all functions, except, perhaps,
Since the solution of the crossword occurs along the lines, the type corresponding to the entire field is a set of all horizontal and vertical lines, although this leads to duplication of all the cells of the crossword.
Each line stores information about cells and blocks (a block corresponds to a number in a condition).
Information about the cells is stored in the form of two bit masks of the same length, representing filled and blocked cells.
The block, in addition to the number itself, contains a mask that corresponds to the area of the line in which the given block can be.
At the beginning of the solution, the masks of filled and blocked cells are empty, and the mask of the block, on the contrary, is completely filled. This means that all cells are empty, and each block can be in any part of the line. The solution process comes down to narrowing the area of each block to sizes equal to its number and filling in the masks accordingly.
All of the above types (except
The only function of the class
The class
From the description of the functions of the class
Field consistency is ensured by synchronization of horizontal and vertical lines. Thus, if a cell is in some state (painted over, blocked, or empty) in a horizontal line, then it is in exactly the same state in the corresponding vertical line, and vice versa.
We will talk about the consistency of the line later, since it is directly related to the decision process.
The consistency of the block is provided non-trivially: for it, it is necessary to exclude from the block area those continuous parts that cannot accommodate it. Thus, if a mask is excluded from the block region with the number 3 and the original region
mask is excluded from the block region with the number 3 and the original region  (for example, because this cell was blocked), then the final result of this operation will be a block with an region
(for example, because this cell was blocked), then the final result of this operation will be a block with an region  , but not at all
, but not at all  .
.
For the mask, the consistency is obvious and has already been described above: you cannot paint and block the same cell at the same time.
The operations of converting masks and blocks are very limited, since in the process of solving the cells you can only paint over and block (change your mind, take the eraser and erase it no longer), and the block area can only be narrowed.
The decision process will be considered in separate parts, until they finally form the big picture.
To begin, we will restore the gap left in the section on consistency, and declare that the line is considered consistent if its mask is filled in accordance with its blocks. Two points are hidden behind this phrase. Firstly, those cells that do not fall into the region to any block must be blocked (if the line does not contain a single block, then, accordingly, all cells are such).
Secondly, for each block using the function,
(Note: here we finally used the functions
Thus, as mentioned earlier, the consistency condition for a line ensures that its mask will always be completed if all of its blocks are completed.
The decision within the line essentially boils down to two transformations.
The first transformation, in fact, is the inverse of the consistency condition: it ensures that the blocks will be completed if the mask is completed. Three actions are used for this.
If we take the leftmost of all the blocks, which, in principle, can contain some shaded part of the mask, then its rightmost position will be limited to this mask itself, because if it moves even more to the right, then there will be no one to give this shaded area to. The same considerations are true for the rightmost of these blocks.
Applying this reasoning to each continuous part of the mask, we obtain the second line transformation:
The field does not have any special transformations of its own; the only option for it is to take some ready-made transformation and apply it to all its lines.
Since solving Japanese crosswords is an NP-complete task, you won’t be able to do without branching. Branching is defined by a function of the type
The simplest way is branching into cells: each empty cell generates one element of the external list, which in turn is a list of two elements, in one of which this cell is filled and blocked in the other.
Another branching method is also available for the line: for each continuous shaded part of the mask (external list), you can consider a set of blocks that can contain it (internal list), as options that define branches.
It makes sense to apply most of the transformations iteratively. In this case, you can simply apply the transformation until it changes at least something, or you can (in the case when unnecessary application may take considerable time) pre-check the object for completeness.
Branch results can be processed regardless of the particular data type and branch method. To do this, applying a certain branching method, and then applying some transformation to each resulting object, it is necessary to take the average value for each set of mutually exclusive branches, and then synchronize these averaged objects obtained by different branch points. I will not describe it in detail, but an optimized version related to completeness check is also available for this operation.
Finally, if all else fails, you can go into recursion. Only in this way can you get all the solutions, if there are several.
All. The tools available are enough to get the solver in a few simple steps.
The program works pretty fast on crosswords that have a single solution: out of the thousands of crosswords I have on my laptop, only two (including the one made in the preface) are solved for more than a minute, almost all fit in 10 seconds, and none of them required recursion.
Theoretically, with some refinement, the program can be used to automatically assess the complexity of crosswords (since the solution methods are generally similar to those used by a person) and evidence of the uniqueness of the solution; export to LaTeX is available, and may even appear in SVN soon. So, if you wish, you can organize a home issue of magazines :)
At some point, I wanted to “teach the computer” to solve Japanese crosswords as I myself solve them. No lofty goal, just for fun. Then methods were added that I myself can’t apply due to the limited capabilities of the human brain, but, in fairness, the program copes with all the crosswords from the magazines without them.
So, the task is simple: solve a crossword puzzle, and if there are many solutions, then find them all. The solution is written in Haskell, and although the code substantially complements the verbal description, even without knowledge of the language, the general essence can be understood. If you want to feel the result live, on the project page you can download the sources (I did not upload binary assemblies). Solutions are exported to Binary PBM, and you can extract conditions from it.
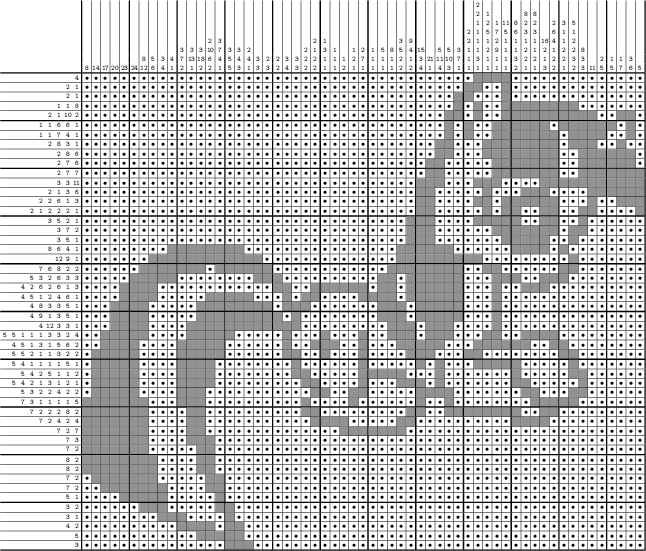
Despite the fact that I tried to write as clearly as possible, I did not fully succeed. Under the cut a lot of letters and code and almost no pictures.
Bitmask
At the heart of the whole program is your bike for a bit mask. It is not too fast, but it has a property that was important to me in the debugging process: it crashes during operations that do not make sense, namely during any operation on masks of different lengths. I will give here only the signatures of the functions and the picture explaining the principle of their work; the implementation is very primitive and has no direct relation to the solution.
bmCreate :: Int -> BitMask
bmLength :: BitMask -> Int
bmSize :: BitMask -> Int
bmIsEmpty :: BitMask -> Bool
bmNot :: BitMask -> BitMask
bmAnd :: BitMask -> BitMask -> BitMask
bmOr :: BitMask -> BitMask -> BitMask
bmIntersection :: [BitMask] -> BitMask
bmUnion :: [BitMask] -> BitMask
bmSplit :: BitMask -> [BitMask]
bmByOne :: BitMask -> [BitMask]
bmExpand :: BitMask -> BitMask
bmFillGaps :: BitMask -> BitMask
bmLeftIncursion :: Int -> BitMask -> BitMask
bmRightIncursion :: Int -> BitMask -> BitMask
bmTranspose :: [BitMask] -> [BitMask]

I think that this graphic description exhaustively for all functions, except, perhaps,
bmLeftIncursionand bmRightIncursion. Why they are needed, it will be clear later, the principle of their work is as follows: it bmLeftIncursionfinds the leftmost filled bit and creates a mask in which all the bits before it are filled, as well as as many bits starting with it as were specified when the function was called; the second function works similarly.Structure
Since the solution of the crossword occurs along the lines, the type corresponding to the entire field is a set of all horizontal and vertical lines, although this leads to duplication of all the cells of the crossword.
data Field = Field {
flHorLines :: [Line],
flVerLines :: [Line]
} deriving Eq
Each line stores information about cells and blocks (a block corresponds to a number in a condition).
data Line = Line {
lnMask :: LineMask,
lnBlocks :: [Block]
} deriving Eq
Information about the cells is stored in the form of two bit masks of the same length, representing filled and blocked cells.
data LineMask = LineMask {
lmFilledMask :: BitMask,
lmBlockedMask :: BitMask
} deriving Eq
The block, in addition to the number itself, contains a mask that corresponds to the area of the line in which the given block can be.
data Block = Block {
blScopeMask :: BitMask,
blNumber :: Int
} deriving Eq
At the beginning of the solution, the masks of filled and blocked cells are empty, and the mask of the block, on the contrary, is completely filled. This means that all cells are empty, and each block can be in any part of the line. The solution process comes down to narrowing the area of each block to sizes equal to its number and filling in the masks accordingly.
Completion and synchronization
All of the above types (except
BitMask) are instances of two classes: Completableand Syncable. The only function of the class
Completableis the "completeness" of the object. A field is considered completed if all its lines are completed. A line is completed if all its blocks are completed; at the same time, it is unnecessary to demand the completion of the mask (it follows from the completeness of the blocks; why, again, it will be clear a little later). To complete the block, as mentioned above, it is necessary that the size of its area coincides with its number.class Completable a where
clIsCompleted :: a -> Bool
instance Completable Field where
clIsCompleted fl = all clIsCompleted (flHorLines fl) && all clIsCompleted (flVerLines fl)
instance Completable Line where
clIsCompleted ln = all clIsCompleted (lnBlocks ln)
instance Completable Block where
clIsCompleted bl = bmSize (blScopeMask bl) == blNumber bl
The class
Syncableprovides functions that allow you to bring together different decision branches. snAverageselects from the two branches only the general, and snSync- that manifests itself in at least one branch (we can consider them generalizations of functions bmAndand, bmOraccordingly). snAverageAlland snSyncAllthey do exactly the same thing, but they work not with two objects, but with lists of objects.class Syncable a where
snSync :: a -> a -> Maybe a
sn1 `snSync` sn2 = snSyncAll [sn1, sn2]
snAverage :: a -> a -> Maybe a
sn1 `snAverage` sn2 = snAverageAll [sn1, sn2]
snSyncAll :: [a] -> Maybe a
snSyncAll [] = Nothing
snSyncAll sns = foldr1 (wrap snSync) (map return sns)
snAverageAll :: [a] -> Maybe a
snAverageAll [] = Nothing
snAverageAll sns = foldr1 (wrap snAverage) (map return sns)
wrap :: Monad m => (a -> b -> m c) -> m a -> m b -> m c
wrap f mx my = do
x <- mx
y <- my
f x y
Coherence
From the description of the functions of the class
Syncableit can be seen that their result is an object wrapped in a monad Maybe. In fact, this manifests the important concept of consistency, which is also defined for all of the above types, but has not been moved to a separate class for encapsulation reasons. As an example, the same cell cannot be simultaneously filled and locked; if any operation can lead to such a situation, then it is marked with a monad Maybe(as a rule, it is of type type TransformFunction a = a -> Maybe a), and if it leads to this situation, then it will result Nothing, because no object in the program can exist in an inconsistent state . BecauseNothing, in turn, cannot be an integral part of other objects, the whole field will become uncoordinated, which will mean the absence of solutions. Field consistency is ensured by synchronization of horizontal and vertical lines. Thus, if a cell is in some state (painted over, blocked, or empty) in a horizontal line, then it is in exactly the same state in the corresponding vertical line, and vice versa.
flEnsureConsistency :: TransformFunction Field
flEnsureConsistency fl = do
let lnsHor = flHorLines fl
let lnsVer = flVerLines fl
lnsHor' <- zipWithM lnSyncWithLineMask (lmTranspose $ map lnMask lnsVer) lnsHor
lnsVer' <- zipWithM lnSyncWithLineMask (lmTranspose $ map lnMask lnsHor) lnsVer
return $ Field lnsHor' lnsVer'
lnSyncWithLineMask :: LineMask -> TransformFunction Line
lnSyncWithLineMask lm ln = do
lm' <- lm `snSync` lnMask ln
return ln { lnMask = lm' }
We will talk about the consistency of the line later, since it is directly related to the decision process.
The consistency of the block is provided non-trivially: for it, it is necessary to exclude from the block area those continuous parts that cannot accommodate it. Thus, if a
 mask is excluded from the block region with the number 3 and the original region
mask is excluded from the block region with the number 3 and the original region  (for example, because this cell was blocked), then the final result of this operation will be a block with an region
(for example, because this cell was blocked), then the final result of this operation will be a block with an region  , but not at all
, but not at all  .
.blEnsureConsistency :: TransformFunction Block
blEnsureConsistency bl = do
let bms = filter ((blNumber bl <=) . bmSize) $ bmSplit $ blScopeMask bl
guard $ not $ null bms
return bl { blScopeMask = bmUnion bms }
For the mask, the consistency is obvious and has already been described above: you cannot paint and block the same cell at the same time.
lmEnsureConsistency :: TransformFunction LineMask
lmEnsureConsistency lm = do
guard $ bmIsEmpty $ lmFilledMask lm `bmAnd` lmBlockedMask lm
return lm
Conversions
The operations of converting masks and blocks are very limited, since in the process of solving the cells you can only paint over and block (change your mind, take the eraser and erase it no longer), and the block area can only be narrowed.
lmFill :: BitMask -> TransformFunction LineMask
lmFill bm lm = lmEnsureConsistency lm { lmFilledMask = lmFilledMask lm `bmOr` bm }
lmBlock :: BitMask -> TransformFunction LineMask
lmBlock bm lm = lmEnsureConsistency lm { lmBlockedMask = lmBlockedMask lm `bmOr` bm }
blExclude :: BitMask -> TransformFunction Block
blExclude bm bl = blEnsureConsistency $ bl { blScopeMask = blScopeMask bl `bmAnd` bmNot bm }
blKeep :: BitMask -> TransformFunction Block
blKeep bm bl = blEnsureConsistency $ bl { blScopeMask = blScopeMask bl `bmAnd` bm }
Decision
The decision process will be considered in separate parts, until they finally form the big picture.
Line Consistency
To begin, we will restore the gap left in the section on consistency, and declare that the line is considered consistent if its mask is filled in accordance with its blocks. Two points are hidden behind this phrase. Firstly, those cells that do not fall into the region to any block must be blocked (if the line does not contain a single block, then, accordingly, all cells are such).
lnUpdateBlocked :: [Block] -> TransformFunction LineMask
lnUpdateBlocked [] lm = lmBlock (bmNot $ lmBlockedMask lm) lm
lnUpdateBlocked bls lm = lmBlock (bmNot $ bmUnion $ map blScopeMask bls) lm
Secondly, for each block using the function,
blToFillMaskyou can get a mask that you need to paint over. It is the intersection of two masks that result if you “drive” the block into the leftmost and rightmost parts of its area.blMinimumLeftMask :: Block -> BitMask
blMinimumLeftMask bl = bmLeftIncursion (blNumber bl) (blScopeMask bl)
blMinimumRightMask :: Block -> BitMask
blMinimumRightMask bl = bmRightIncursion (blNumber bl) (blScopeMask bl)
blToFillMask :: Block -> BitMask
blToFillMask bl = blMinimumLeftMask bl `bmAnd` blMinimumRightMask bl
lnUpdateFilled :: [Block] -> TransformFunction LineMask
lnUpdateFilled [] = return
lnUpdateFilled bls = lmFill (bmUnion $ map blToFillMask bls)
(Note: here we finally used the functions
bmLeftIncursionand bmRightIncursion. Strictly speaking, if they were used only for this purpose, we would most likely look a little different, namely, we wouldn’t fill the bit mask until the very first bit of the original mask .)Thus, as mentioned earlier, the consistency condition for a line ensures that its mask will always be completed if all of its blocks are completed.
lnEnsureConsistency :: TransformFunction Line
lnEnsureConsistency ln = do
let bls = lnBlocks ln
lm <- lnUpdateBlocked bls >=> lnUpdateFilled bls $ lnMask ln
return $ ln { lnMask = lm }
Simple line conversion
The decision within the line essentially boils down to two transformations.
The first transformation, in fact, is the inverse of the consistency condition: it ensures that the blocks will be completed if the mask is completed. Three actions are used for this.
- All blocked cells should be excluded from the areas of all blocks.
lnRemoveBlocked :: LineMask -> TransformFunction [Block] lnRemoveBlocked = mapM . blExclude . lmBlockedMask - If the block cannot accommodate any continuous shaded part of the mask (that is, if it creeps out of the block area or has a size larger than its number), then it should be excluded from the block area.
lnRemoveFilled :: LineMask -> TransformFunction [Block] lnRemoveFilled lm = mapM (\ bl -> foldM f bl $ bmSplit $ lmFilledMask lm) where f bl bm = if blCanContainMask bm bl then return bl else blExclude (bmExpand bm) bl blCanContainMask :: BitMask -> Block -> Bool blCanContainMask bm bl = let bm' = bmFillGaps bm in bmSize bm' <= blNumber bl && bmIsEmpty (bm' `bmAnd` bmNot (blScopeMask bl)) - From the area of each block,
blMinimumLeftMaskits left neighbor andblMinimumRightMaskright neighbor should be excluded (here they are already needed exactly in the form described above). To be precise, these masks expanded by one cell are excluded, since there must be at least one empty cell between the blocks.lnExcludeNeighbours :: TransformFunction [Block] lnExcludeNeighbours bls = sequence $ scanr1 (flip $ wrap $ blExclude . bmExpand . blMinimumRightMask) $ scanl1 (wrap $ blExclude . bmExpand . blMinimumLeftMask) $ map return bls
slLoopwill be described later):lnSimpleTransform :: TransformFunction Line
lnSimpleTransform ln = do
let lm = lnMask ln
bls <- lnRemoveBlocked lm >=> slLoop (lnRemoveFilled lm >=> lnExcludeNeighbours) $ lnBlocks ln
lnEnsureConsistency ln { lnBlocks = bls }
Second line conversion
If we take the leftmost of all the blocks, which, in principle, can contain some shaded part of the mask, then its rightmost position will be limited to this mask itself, because if it moves even more to the right, then there will be no one to give this shaded area to. The same considerations are true for the rightmost of these blocks.
lnExtremeOwners :: BitMask -> TransformFunction [Block]
lnExtremeOwners bm bls = do
bls' <- fmap reverse $ maybe (return bls) (f bmLeftIncursion bls) (h bls)
fmap reverse $ maybe (return bls') (f bmRightIncursion bls') (h bls')
where
f g = varyNth (\ bl -> blKeep (g (blNumber bl) bm) bl)
h = findIndex (blCanContainMask bm)
varyNth :: Monad m => (a -> m a) -> [a] -> Int -> m [a]
varyNth f xs idx = do
let (xs1, x : xs2) = splitAt idx xs
x' <- f x
return $ xs1 ++ x' : xs2
Applying this reasoning to each continuous part of the mask, we obtain the second line transformation:
lnTransformByExtremeOwners :: TransformFunction Line
lnTransformByExtremeOwners ln = do
bls <- foldM (flip lnExtremeOwners) (lnBlocks ln) $ bmSplit $ lmFilledMask $ lnMask ln
lnEnsureConsistency ln { lnBlocks = bls }
Field Conversions
The field does not have any special transformations of its own; the only option for it is to take some ready-made transformation and apply it to all its lines.
flTransformByLines :: TransformFunction Line -> TransformFunction Field
flTransformByLines f fl = do
lnsHor <- mapM f (flHorLines fl)
fl' <- flEnsureConsistency fl { flHorLines = lnsHor }
lnsVer <- mapM f (flVerLines fl')
flEnsureConsistency fl' { flVerLines = lnsVer }
Branches
Since solving Japanese crosswords is an NP-complete task, you won’t be able to do without branching. Branching is defined by a function of the type
type ForkFunction a = a -> [[a]]where the internal list includes mutually exclusive options, and the external one - various ways to produce these options. The simplest way is branching into cells: each empty cell generates one element of the external list, which in turn is a list of two elements, in one of which this cell is filled and blocked in the other.
lnForkByCells :: ForkFunction Line
lnForkByCells ln = do
let lm = lnMask ln
bm <- bmByOne $ lmEmptyMask lm
return $ do
lm' <- [fromJust $ lmBlock bm lm, fromJust $ lmFill bm lm]
maybeToList $ lnEnsureConsistency ln { lnMask = lm' }
flForkByCells :: ForkFunction Field
flForkByCells fl = do
let lnsHor = flHorLines fl
let lnsVer = flVerLines fl
idx <- findIndices (not . clIsCompleted) lnsHor
let (lns1, ln : lns2) = splitAt idx lnsHor
lns <- lnForkByCells ln
return $ do
ln' <- lns
maybeToList $ flEnsureConsistency $ Field (lns1 ++ ln' : lns2) lnsVer
Another branching method is also available for the line: for each continuous shaded part of the mask (external list), you can consider a set of blocks that can contain it (internal list), as options that define branches.
lnForkByOwners :: ForkFunction Line
lnForkByOwners ln = do
let bls = lnBlocks ln
bm <- bmSplit $ lmFilledMask $ lnMask ln
case findIndices (blCanContainMask bm) bls of
[_] -> []
idxs -> return $ do
idx <- idxs
maybeToList $ do
bls' <- varyNth (g bm) bls idx
lnEnsureConsistency ln { lnBlocks = bls' }
where g bm bl = blKeep ((bmAnd `on` ($ bm) . ($ blNumber bl)) bmLeftIncursion bmRightIncursion) bl
Generalized Functions
It makes sense to apply most of the transformations iteratively. In this case, you can simply apply the transformation until it changes at least something, or you can (in the case when unnecessary application may take considerable time) pre-check the object for completeness.
slLoop :: Eq a => TransformFunction a -> TransformFunction a
slLoop f x = do
x' <- f x
if x == x' then return x else slLoop f x'
slSmartLoop :: (Completable a, Eq a) => TransformFunction a -> TransformFunction a
slSmartLoop f x
| clIsCompleted x = return x
| otherwise = do
x' <- f x
if x == x' then return x else slLoop f x'
Branch results can be processed regardless of the particular data type and branch method. To do this, applying a certain branching method, and then applying some transformation to each resulting object, it is necessary to take the average value for each set of mutually exclusive branches, and then synchronize these averaged objects obtained by different branch points. I will not describe it in detail, but an optimized version related to completeness check is also available for this operation.
slForkAndSyncAll :: (Syncable a) => ForkFunction a -> TransformFunction a -> TransformFunction a
slForkAndSyncAll f g x = do
xs <- mapM (snAverageAll . mapMaybe g) $ f x
snSyncAll (x : xs)
slForkAndSmartSync :: (Syncable a, Completable a, Eq a) => ForkFunction a -> TransformFunction a -> TransformFunction a
slForkAndSmartSync f g x = foldr h (return x) (f x) where
h xs mx = do
x' <- mx
if clIsCompleted x' then mx else case mapMaybe (snSync x') xs of
[] -> Nothing
xs' -> case filter (/= x') xs' of
[] -> return x'
xs'' -> snAverageAll . mapMaybe g $ xs''
Finally, if all else fails, you can go into recursion. Only in this way can you get all the solutions, if there are several.
slAllSolutions :: (Completable a) => ForkFunction a -> TransformFunction a -> a -> [a]
slAllSolutions f g x = do
x' <- maybeToList $ g x
if clIsCompleted x' then return x' else case f x' of
(xs : _) -> do
x'' <- xs
slAllSolutions f g x''
[] -> []
Fin venko
All. The tools available are enough to get the solver in a few simple steps.
- Combine two line transforms.
lineTransform = slSmartLoop $ lnSimpleTransform >=> lnTransformByExtremeOwners - We process line-specific branching.
lineTransform' = slForkAndSyncAll lnForkByOwners lineTransform - Составим из этих двух преобразований преобразование поля.
fieldTransform = slSmartLoop $ slSmartLoop (flTransformByLines lineTransform) >=> flTransformByLines lineTransform' - Обработаем результаты ветвления поля по клеткам.
fieldTransform' = slForkAndSmartSync flForkByCells fieldTransform - Объединим предыдущие два преобразования.
fieldTransform'' = slSmartLoop $ fieldTransform >=> fieldTransform' - И, наконец, добавим рекурсию.
solve = slAllSolutions flForkByCells fieldTransform''
Послесловие
The program works pretty fast on crosswords that have a single solution: out of the thousands of crosswords I have on my laptop, only two (including the one made in the preface) are solved for more than a minute, almost all fit in 10 seconds, and none of them required recursion.
Theoretically, with some refinement, the program can be used to automatically assess the complexity of crosswords (since the solution methods are generally similar to those used by a person) and evidence of the uniqueness of the solution; export to LaTeX is available, and may even appear in SVN soon. So, if you wish, you can organize a home issue of magazines :)
