How are loan interest accrued and how to apply it
Hello! When I took a mortgage, I decided to thoroughly understand how interest is accrued, how best to make an advance payment, and so on. I myself am an economist. In general, I share, I hope it will be useful.
The loan payment consists of two parts - interest to the bank and repayment of the main debt.
In this case, monthly accrued interest is calculated by the formula:

Based on this:
I will give calculations for each item.
1. The highest interest at the beginning
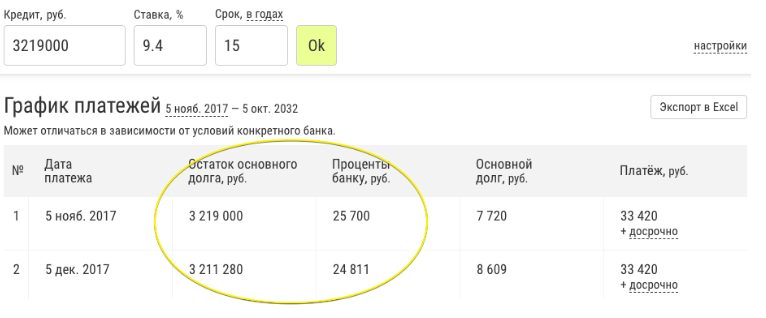
Start of term

End of term
2. The amount of interest depends on the number of days in a month
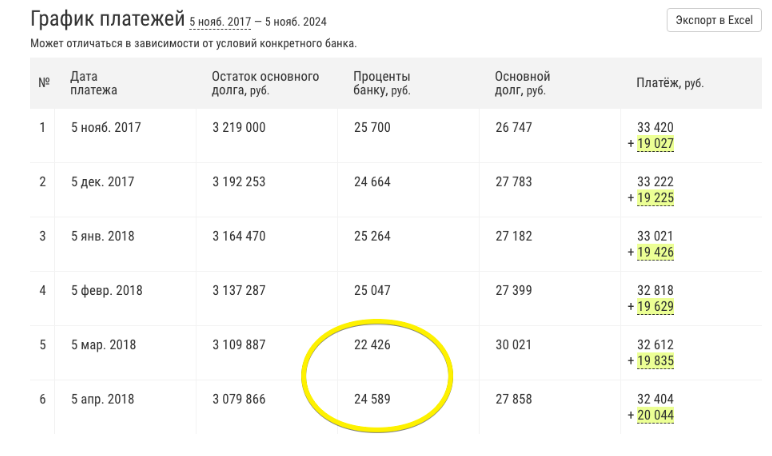
For February (i.e., for 28 days) in March 22 thousand were accrued, and for March (i.e., for 31 days) in April - 25 thousand.
We count 3 options.
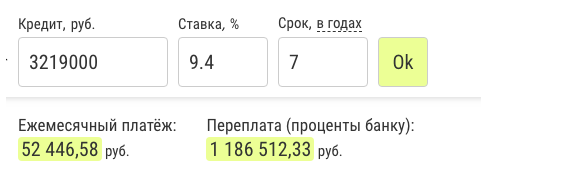
Option 1

Option 2
We received that for a period of 15 years the overpayment is 1.6 million more.
Now set the early repayments so that the payment is obtained, as in 7 years.
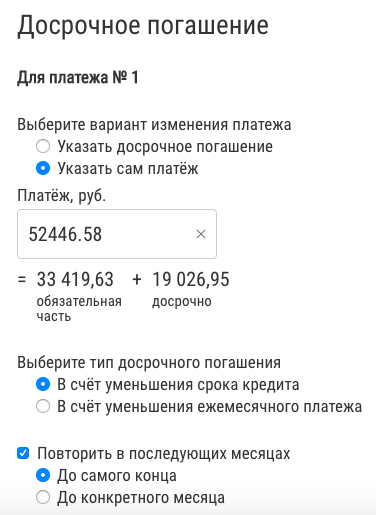
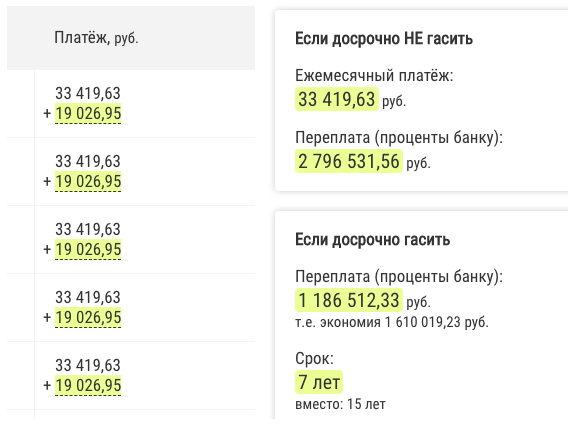
We fix the payment of 52 thousand before the end of the term.
We reached the same overpayment of 1.2 million and the same term of 7 years:
Option 3
Comparison table
4. Equally profitable to make early repayment with a reduction in the term and payment
In the previous paragraph, early repayments were made with a shorter period. Now count them with a reduction in payment.
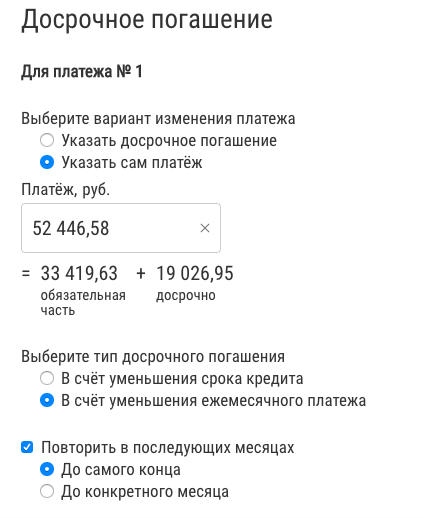
We fix the payment of 52 thousand before the end of the term with a decrease in the payment.
Comparison table
The main conclusion is that the amount of the overpayment is determined solely by the size of the monthly payment (mandatory part + prepayment), and not by the initial loan term, the type of prepayment, etc., since the monthly accrued interest depends only on the balance of the main debt. My tactic is better to be safe, taking for a longer period and paying off with a decrease in payment, but pay it early every month. Morally lighter, but the overpayment is the same.
The loan payment consists of two parts - interest to the bank and repayment of the main debt.
In this case, monthly accrued interest is calculated by the formula:

Based on this:
- The amount of monthly accrued interest is the largest at the beginning, because at the beginning the largest balance of the main debt. As it decreases, interest also decreases.
- The amount of interest “jumps” from month to month, because it depends on the number of days in a month.
- The loan term in the calculation of monthly accrued interest does not appear, which means that it does not matter for how long to take a mortgage - the overpayment will be the same if the monthly payments are the same.
- If you make a partial early repayment with a decrease in the monthly payment, the overpayment will be exactly the same as in the case of a shorter period, if you continue to pay the previous monthly payment, and not reduced.
I will give calculations for each item.
1. The highest interest at the beginning

Start of term

End of term
2. The amount of interest depends on the number of days in a month

For February (i.e., for 28 days) in March 22 thousand were accrued, and for March (i.e., for 31 days) in April - 25 thousand.
3. The overpayment is the same for different starting dates
We count 3 options.
- Mortgage for 7 years.
- Mortgage for 15 years.
- Mortgage for 15 years with early repayments.

Option 1

Option 2
We received that for a period of 15 years the overpayment is 1.6 million more.
Now set the early repayments so that the payment is obtained, as in 7 years.

We fix the payment of 52 thousand before the end of the term.
We reached the same overpayment of 1.2 million and the same term of 7 years:

Option 3
Comparison table
| Term, years | Monthly payment, rub. | Overpayment, million | Link to the calculation |
|---|---|---|---|
| 7 | 52 thousand | 1,2 | Payment |
| fifteen | 33 thousand | 2,8 | Payment |
| 15 → 7 | 33 thousand mandatory + 19 thousand ahead of schedule | 1,2 | Payment |
4. Equally profitable to make early repayment with a reduction in the term and payment
In the previous paragraph, early repayments were made with a shorter period. Now count them with a reduction in payment.

We fix the payment of 52 thousand before the end of the term with a decrease in the payment.
Comparison table
| Early repayment type | Mandatory payment, rub. | Early repayment, rub. | Total monthly payment, rub. | Overpayment, million | Link to the calculation |
|---|---|---|---|---|---|
| Reduction of term | 33 thousand | 19 thousand | 52 thousand | 1,2 | Payment |
| Payment reduction | 33 thousand → 0.4 thousand | 19 thousand → 52 thousand | 52 thousand | 1,2 | Payment |
The main conclusion is that the amount of the overpayment is determined solely by the size of the monthly payment (mandatory part + prepayment), and not by the initial loan term, the type of prepayment, etc., since the monthly accrued interest depends only on the balance of the main debt. My tactic is better to be safe, taking for a longer period and paying off with a decrease in payment, but pay it early every month. Morally lighter, but the overpayment is the same.
