A brief introduction to Markov chains
- Transfer
In 1998, Lawrence Page, Sergey Brin, Rajiv Motwani and Terry Vinograd published the article “The PageRank Citation Ranking: Bringing Order to the Web”, which described the now famous PageRank algorithm, which became the foundation of Google. After a little less than two decades, Google became a giant, and even though its algorithm has evolved strongly, PageRank is still a “symbol” of Google ranking algorithms (although only a few people can really tell how much weight it takes in the algorithm today) .
From a theoretical point of view, it is interesting to note that one of the standard interpretations of the PageRank algorithm is based on a simple but fundamental concept of Markov chains. From the article we will see that Markov chains are powerful tools for stochastic modeling that can be useful to any data scientist. In particular, we will answer such basic questions: what are Markov chains, what good properties do they possess, and what can be done with their help?
Short review
In the first section, we give the basic definitions necessary for understanding Markov chains. In the second section, we consider the special case of Markov chains in a finite state space. In the third section, we consider some of the elementary properties of Markov chains and illustrate these properties with many small examples. Finally, in the fourth section, we associate the Markov chains with the PageRank algorithm and see with an artificial example how Markov chains can be used to rank the nodes of a graph.
Note. Understanding this post requires knowledge of the basics of probability and linear algebra. In particular, the following concepts will be used: conditional probability , eigenvector, and full probability formula .
What are Markov chains?
Random variables and random processes
Before introducing the concept of Markov chains, let us briefly recall the basic, but important concepts of probability theory.
First, outside of the language of mathematics, a random variable X is a quantity that is determined by the result of a random phenomenon. Its result may be a number (or "similarity of a number", for example, vectors) or something else. For example, we can define a random variable as the result of a die roll (number) or as the result of a coin toss (not a number, unless we designate, for example, “eagle” as 0, but “tails” as 1). We also mention that the space of possible results of a random variable can be discrete or continuous: for example, a normal random variable is continuous, and a Poisson random variable is discrete.
Next we can definerandom process(also called stochastic) as a set of random variables indexed by the set T, which often denotes different points in time (in the future we will assume this). The two most common cases: T can be either a set of natural numbers (random process with discrete time), or a set of real numbers (random process with continuous time). For example, if we throw a coin every day, we will set a random process with discrete time, and the ever-changing value of an option on the exchange will set a random process with continuous time. Random variables at different points in time can be independent of each other (an example with a coin toss), or have some kind of dependence (an example with the option value); Moreover,
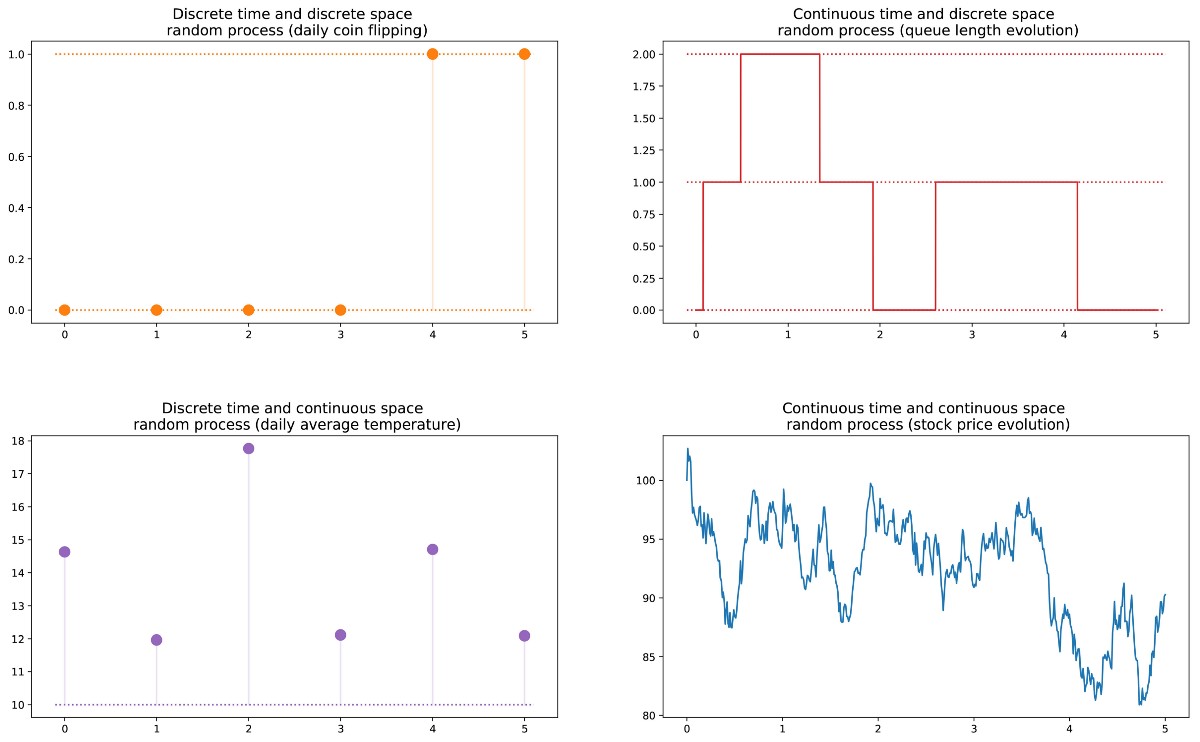
Different types of random processes (discrete / continuous in space / time).
Markov property and Markov chain
There are well-known families of random processes: Gaussian processes, Poisson processes, autoregressive models, moving average models, Markov chains, and others. Each of these individual cases has certain properties that allow us to better explore and understand them.
One of the properties that greatly simplifies the study of a random process is the Markov property. If we explain it in a very informal language, then the Markov property tells us that if we know the value obtained by some random process at a given moment in time, then we will not receive any additional information about the future behavior of the process, collecting other information about its past. In a more mathematical language: at any moment in time, the conditional distribution of future states of a process with given current and past states depends only on the current state, and not on past states (the property of lack of memory ). A random process with a Markov property is called a Markov process .
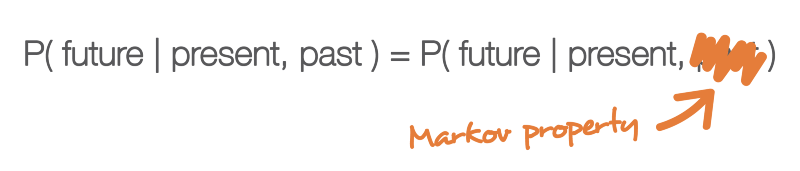
The Markov property means that if we know the current state at a given moment in time, then we do not need any additional information about the future, collected from the past.
Based on this definition, we can formulate the definition of “homogeneous Markov chains with discrete time” (hereinafter for simplicity we will call them “Markov chains”). The Markov chain is a Markov process with discrete time and a discrete state space. So, a Markov chain is a discrete sequence of states, each of which is taken from a discrete state space (finite or infinite), satisfying the Markov property.
Mathematically, we can denote the Markov chain as follows:
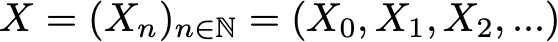
where at each moment of time the process takes its values from a discrete set E, such that

Then the Markov property implies that we have
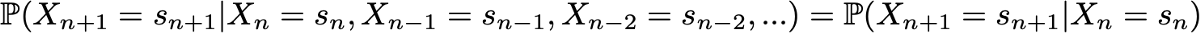
Note again that this last formula reflects the fact that for the chronology (where I am now and where I was before), the probability distribution of the next state (where I will be next) depends on the current state, but not on past states.
Note. In this introductory post, we decided to talk only about simple homogeneous Markov chains with discrete time. However, there are also inhomogeneous (time-dependent) Markov chains and / or continuous-time chains. In this article we will not consider such variations of the model. It is also worth noting that the above definition of a Markov property is extremely simplified: the true mathematical definition uses the concept of filtering, which goes far beyond our introductory acquaintance with the model.
We characterize the randomness dynamics of a Markov chain
In the previous subsection, we got acquainted with the general structure corresponding to any Markov chain. Let's see what we need to set a specific "instance" of such a random process.
First, we note that the complete determination of the characteristics of a random process with discrete time that does not satisfy the Markov property can be difficult: the probability distribution at a given point in time may depend on one or more moments in the past and / or future. All of these possible time dependencies can potentially complicate the creation of a process definition.
However, due to the Markov property, the dynamics of the Markov chain is quite simple to determine. And indeed. we need to define only two aspects: the initial probability distribution (i.e., the probability distribution at time n = 0), denoted by
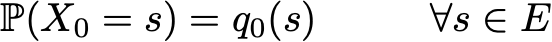
and the transition probability matrix (which gives us the probabilities that the state at time n + 1 is the next for another state at time n for any pair of states), denoted by
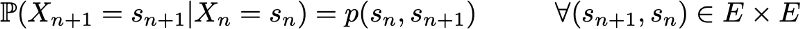
If these two aspects are known, then the full (probabilistic) dynamics of the process is clearly defined. And in fact, the probability of any result of the process can then be calculated cyclically.
Example: suppose we want to know the probability that the first 3 states of the process will have values (s0, s1, s2). That is, we want to calculate the probability
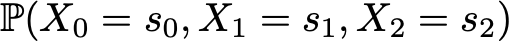
Here we apply the formula for the total probability, which states that the probability of obtaining (s0, s1, s2) is equal to the probability of obtaining the first s0 times the probability of getting s1, given that we previously got s0 times the probability of getting s2 taking into account the fact that we got earlier in order s0 and s1. Mathematically, this can be written as
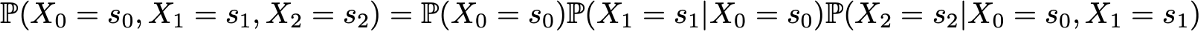
And then simplification is revealed, determined by the Markov assumption. And in fact, in the case of long chains, we obtain strongly conditional probabilities for the latter states. However, in the case of Markov chains, we can simplify this expression by taking advantage of the fact that
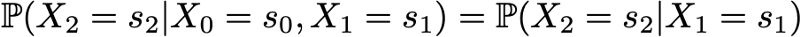
getting this way
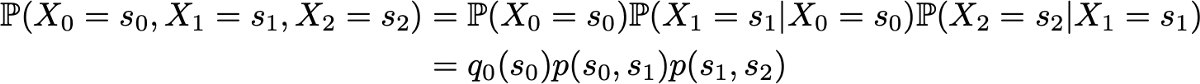
Since they fully characterize the probabilistic dynamics of the process, many complex events can be calculated only on the basis of the initial probability distribution q0 and the transition probability matrix p. It is also worth mentioning one more basic connection: the expression of the probability distribution at time n + 1, expressed with respect to the probability distribution at time n
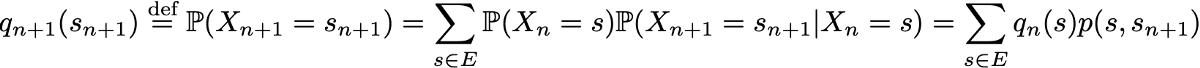
Markov chains in finite state spaces
Matrix and graph representation
Here we assume that the set E has a finite number of possible states N:
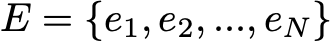
Then the initial probability distribution can be described as a row vector q0 of size N, and transition probabilities can be described as a matrix p of size N by N, such that
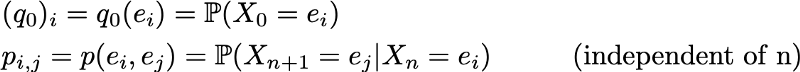
The advantage of this notation is that if we denote the probability distribution in step n by the row vector qn such that its components are specified
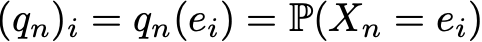
then simple matrix relations are preserved
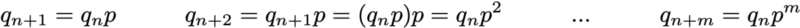
(here we will not consider the proof, but it is very simple to reproduce it).
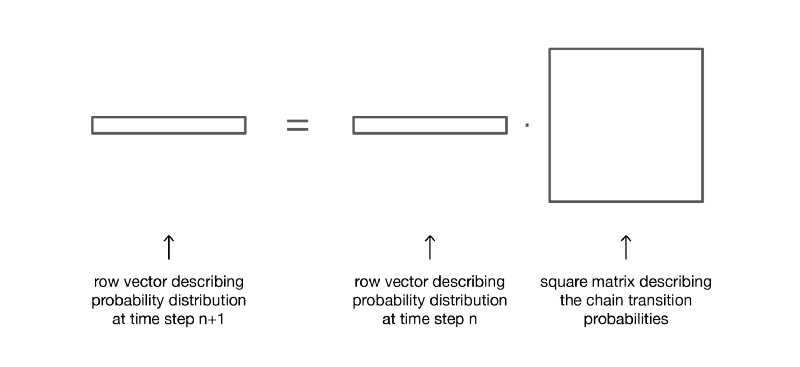
If we multiply the row vector on the right, which describes the probability distribution at a given time stage, by the transition probability matrix, then we get the probability distribution at the next time stage.
So, as we see, the transition of the probability distribution from a given stage to the next is simply defined as the right multiplication of the row vector of probabilities of the initial step by the matrix p. In addition, this implies that we have

The random dynamics of a Markov chain in a finite state space can easily be represented as a normalized oriented graph such that each node of the graph is a state, and for each pair of states (ei, ej) there exists an edge going from ei to ej if p (ei, ej )> 0. Then the edge value will be the same probability p (ei, ej).
Example: a reader of our site
Let's illustrate all this with a simple example. Consider the everyday behavior of a fictitious visitor to a site. Every day he has 3 possible states: the reader does not visit the site that day (N), the reader visits the site, but does not read the entire post (V), and the reader visits the site and reads one entire post (R). So, we have the following state space:
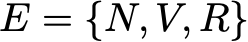
Suppose, on the first day, this reader has a 50% chance of only accessing the site and a 50% chance of visiting the site and reading at least one article. The vector describing the initial probability distribution (n = 0) then looks like this:
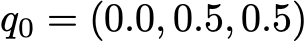
Also imagine that the following probabilities are observed:
- when the reader does not visit one day, then there is a probability of 25% not to visit him the next day, a probability of 50% only to visit him and 25% to visit and read the article
- when the reader visits the site one day, but doesn’t read, then he has a 50% chance to visit it again the next day and not read the article, and a 50% chance to visit and read
- when a reader visits and reads an article on the same day, it has a 33% chance of not logging in the next day (I hope this post will not have such an effect!) , a 33% chance of only logging into the site and 34% of visiting and reading the article again
Then we have the following transition matrix:

From the previous subsection, we know how to calculate for this reader the probability of each state the next day (n = 1)

The probabilistic dynamics of this Markov chain can be graphically represented as follows:

Presentation in the form of a graph of the Markov chain, modeling the behavior of our invented visitor to the site.
Properties of Markov chains
In this section, we will talk only about some of the most basic properties or characteristics of Markov chains. We will not go into mathematical details, but will provide a brief overview of interesting points that must be studied to use Markov chains. As we have seen, in the case of a finite state space, the Markov chain can be represented as a graph. In the future, we will use the graphical representation to explain some properties. However, do not forget that these properties are not necessarily limited to the case of a finite state space.
Decomposability, periodicity, irrevocability and recoverability
In this subsection, let's start with several classic ways of characterizing a state or an entire Markov chain.
First, we mention that the Markov chain is indecomposable if it is possible to reach any state from any other state (it is not necessary that in one step of time). If the state space is finite and the chain can be represented as a graph, then we can say that the graph of an indecomposable Markov chain is strongly connected (graph theory).
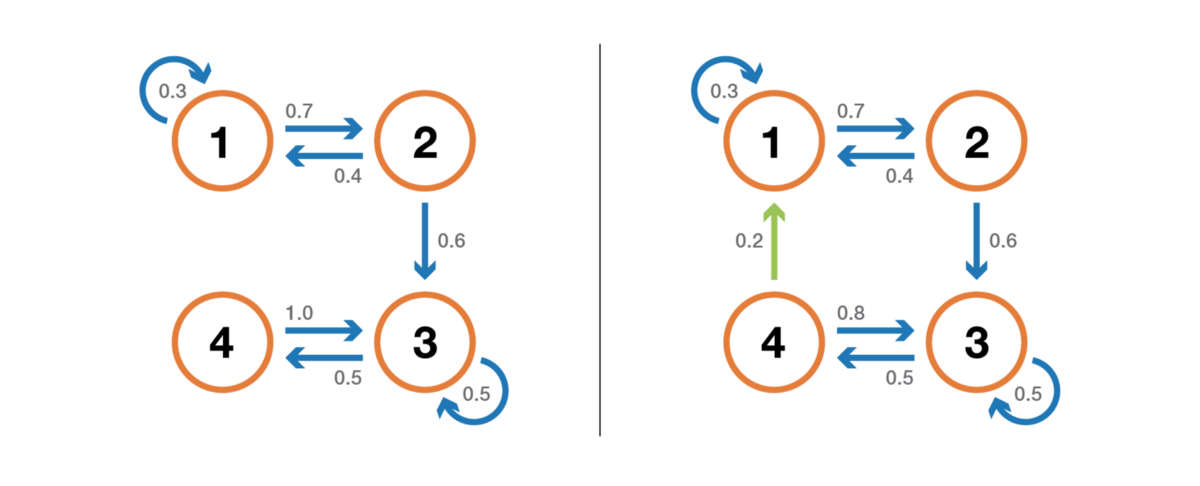
Illustration of the property of indecomposability (irreducibility). The chain on the left cannot be shortened: from 3 or 4 we cannot get into 1 or 2. The chain on the right (one edge is added) can be shortened: each state can be reached from any other.
A state has a period k if, upon leaving it, for any return to this state, the number of time steps is a multiple of k (k is the largest common divisor of all possible lengths of return paths). If k = 1, then they say that the state is aperiodic, and the entire Markov chain is aperiodic if all its states are aperiodic. In the case of an irreducible Markov chain, we can also mention that if one state is aperiodic, then all the others are also aperiodic.
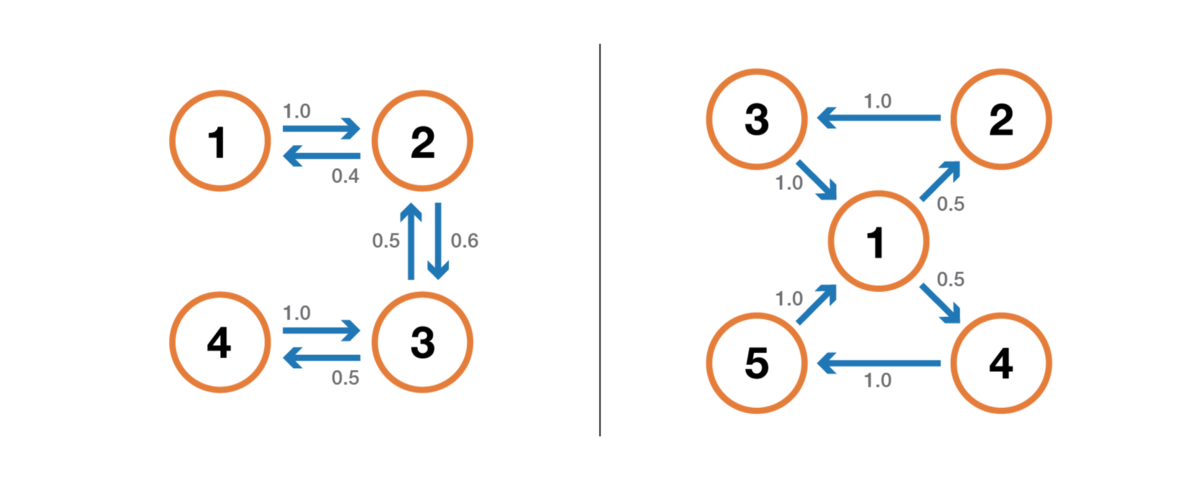
Illustration of the periodicity property. The chain on the left is periodic with k = 2: when leaving any state, returning to it always requires the number of steps multiple of 2. The chain on the right has a period of 3. The
state is irrevocable if, when leaving the state, there is a non-zero probability that we will never be in it we will not return. Conversely, a state is considered to be returnable if we know that after leaving the state we can return to it in the future with probability 1 (if it is not irrevocable).
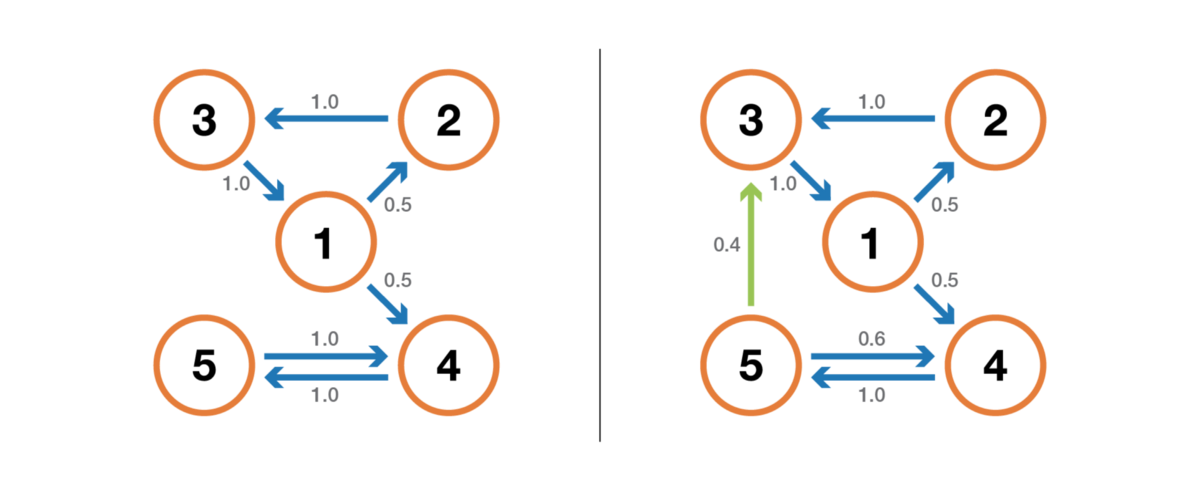
Illustration of the return / irrevocability property. The chain on the left has the following properties: 1, 2 and 3 are irrevocable (when leaving these points we cannot be absolutely sure that we will return to them) and have a period of 3, and 4 and 5 are returnable (when leaving these points we are absolutely sure that someday we’ll return to them) and have a period of 2. The chain on the right has another rib, making the entire chain returnable and aperiodic.
For the return state, we can calculate the average return time, which is the expected return time when leaving the state. Note that even the probability of a return is 1, this does not mean that the expected return time is finite. Therefore, among all the return states, we can distinguish between positive return states(with a finite expected return time) and zero return states (with an infinite expected return time).
Stationary distribution, marginal behavior and ergodicity
In this subsection, we consider properties that characterize some aspects of the (random) dynamics described by the Markov chain.
The probability distribution π over the state space E is called the stationary distribution if it satisfies the expression
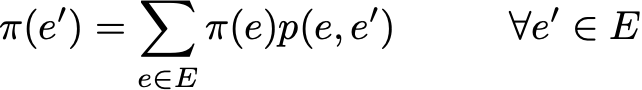
Since we have
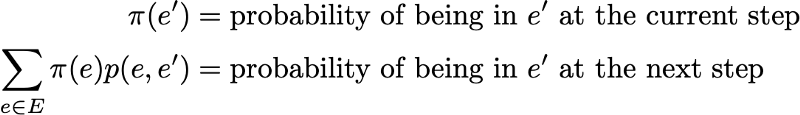
Then the stationary distribution satisfies the expression
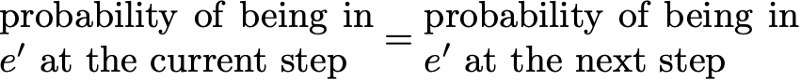
By definition, the stationary probability distribution does not change over time. That is, if the initial distribution q is stationary, then it will be the same at all subsequent stages of time. If the state space is finite, then p can be represented as a matrix, and π as a row vector, and then we get
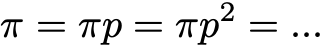
This again expresses the fact that the stationary probability distribution does not change with time (as we see, multiplying the probability distribution on the right by p allows us to calculate the probability distribution at the next stage of time). Keep in mind that an indecomposable Markov chain has a stationary probability distribution if and only if one of its states is positive return.
Another interesting property related to the stationary probability distribution is as follows. If the chain is positive return (that is, there is a stationary distribution in it) and aperiodic, then, whatever the initial probabilities are, the probability distribution of the chain converges as time intervals tend to infinity: they say that the chain has a limiting distribution, which is nothing more than a stationary distribution. In general, it can be written like this:
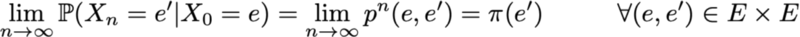
We emphasize once again the fact that we make no assumptions about the initial probability distribution: the probability distribution of the chain reduces to a stationary distribution (equilibrium distribution of the chain) regardless of the initial parameters.
Finally, ergodicity is another interesting property related to the behavior of the Markov chain. If the Markov chain is indecomposable, then it is also said that it is “ergodic” because it satisfies the following ergodic theorem. Suppose we have a function f (.) That goes from the state space E to the axis (this can be, for example, the price of being in each state). We can determine the average value that moves this function along a given trajectory (temporal average). For the nth first terms, this is denoted as
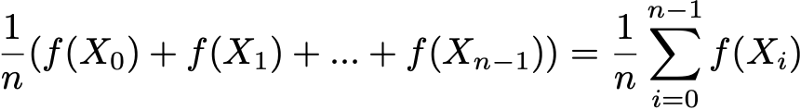
We can also calculate the average value of the function f on the set E, weighted by the stationary distribution (spatial average), which is denoted
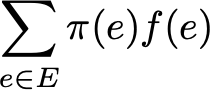
Then the ergodic theorem tells us that when the trajectory becomes infinitely long, the time average is equal to the spatial average (weighted by the stationary distribution). The ergodicity property can be written as follows:
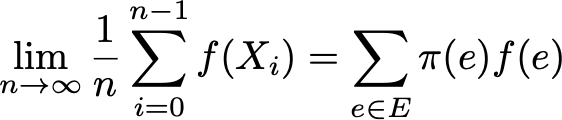
In other words, it means that in the limit earlier the behavior of the trajectory becomes insignificant and only long-term stationary behavior is important when calculating the temporal average.
Let's go back to the example with the site reader
Again, consider the site reader example. In this simple example, it is obvious that the chain is indecomposable, aperiodic and all its states are positively returnable.
To show what interesting results can be calculated using Markov chains, we consider the average time of return to state R (the state “visits the site and reads the article”). In other words, we want to answer the following question: if our reader visits the site one day and reads an article, then how many days will we have to wait on average for him to come back and read the article? Let's try to get an intuitive concept of how this value is calculated.
First we denote
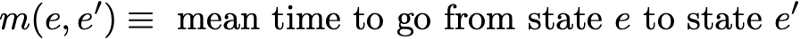
So we want to calculate m (R, R). Talking about the first interval reached after leaving R, we get
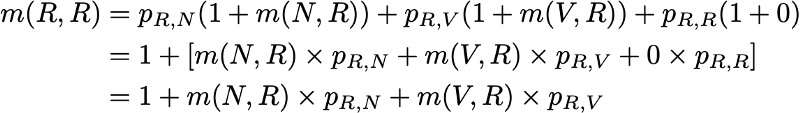
However, this expression requires that for the calculation of m (R, R) we know m (N, R) and m (V, R). These two quantities can be expressed in a similar way:
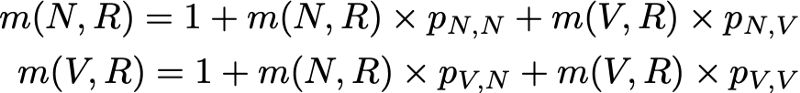
So, we got 3 equations with 3 unknowns and after solving them we get m (N, R) = 2.67, m (V, R) = 2.00 and m (R, R) = 2.54. The average time to return to state R is then 2.54. That is, using linear algebra, we were able to calculate the average time of returning to the state R (as well as the average time of transition from N to R and the average time of transition from V to R).
To finish with this example, let's see what the stationary distribution of the Markov chain will be. To determine the stationary distribution, we need to solve the following equation of linear algebra:
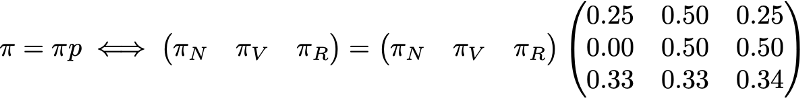
That is, we need to find the left eigenvector p associated with the eigenvector 1. Solving this problem, we obtain the following stationary distribution:
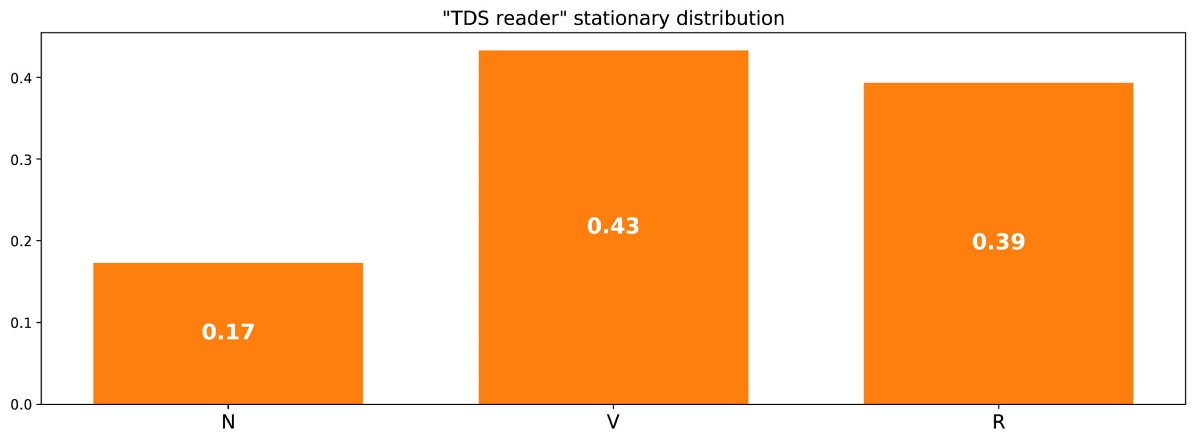
Stationary distribution in the example with the site reader.
You can also notice that π (R) = 1 / m (R, R), and if a little reflection, then this identity is quite logical (but we will not talk about this in detail).
Since the chain is indecomposable and aperiodic, this means that in the long run the probability distribution converges to a stationary distribution (for any initial parameters). In other words, whatever the initial state of the site’s reader, if we wait long enough and randomly select a day, we will get the probability π (N) that the reader will not visit the site that day, the probability π (V) that the reader will stop by but will not read the article, and the probability is π® that the reader will stop by and read the article. To better understand the property of convergence, let's take a look at the following graph showing the evolution of probability distributions starting from different starting points and (quickly) converging to a stationary distribution:
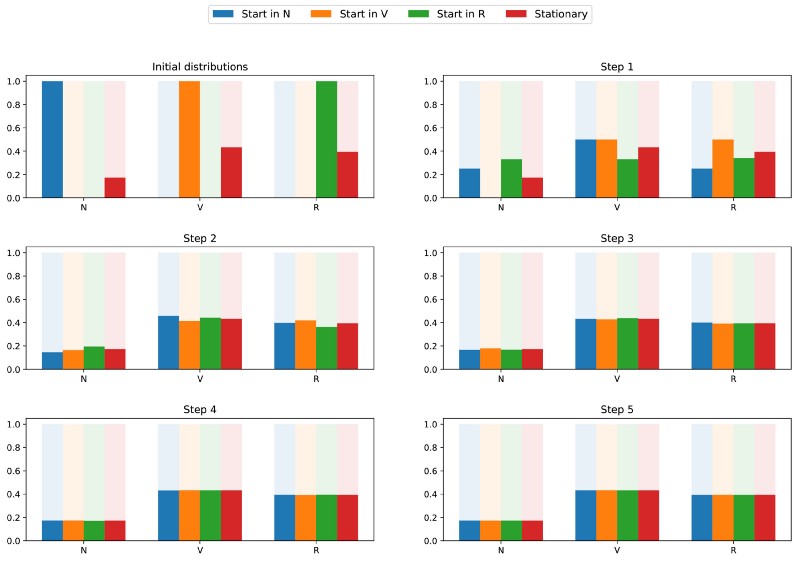
Visualization of the convergence of 3 probability distributions with different initial parameters (blue, orange and green) to the stationary distribution (red).
Classic Example: PageRank Algorithm
It's time to get back to PageRank! But before moving on, it is worth mentioning that the PageRank interpretation given in this article is not the only possible one, and the authors of the original article did not necessarily rely on the use of Markov chains when developing the methodology. However, our interpretation is good because it is very clear.
Arbitrary web user
PageRank is trying to solve the following problem: how can we rank an existing set (we can assume that this set has already been filtered, for example, by some query) using links already existing between the pages?
To solve this problem and be able to rank pages, PageRank approximately performs the following process. We believe that an arbitrary Internet user at the initial time is on one of the pages. Then this user begins to randomly begin to move, clicking on each page on one of the links that lead to another page of the set in question (it is assumed that all links leading outside these pages are prohibited). On any page, all valid links have the same likelihood of clicking.
This is how we define the Markov chain: pages are possible states, transition probabilities are set by links from page to page (weighted in such a way that on every page all linked pages have the same probability of selection), and the properties of lack of memory are clearly determined by user behavior. If we also assume that the given chain is positively returnable and aperiodic (small tricks are used to satisfy these requirements), then in the long run the probability distribution of the “current page” converges to a stationary distribution. That is, whatever the initial page, after a long time, each page has a probability (almost fixed) to become current if we choose a random moment in time.
PageRank is based on the following hypothesis: the most probable pages in a stationary distribution should also be the most important (we visit these pages often because they get links from pages that are also often visited during transitions). Then the stationary probability distribution determines the PageRank value for each state.
Artificial Example
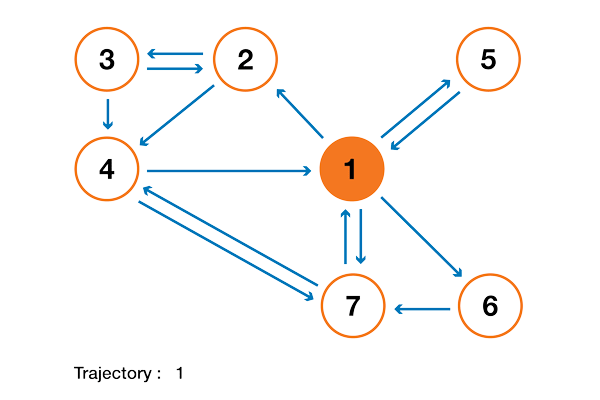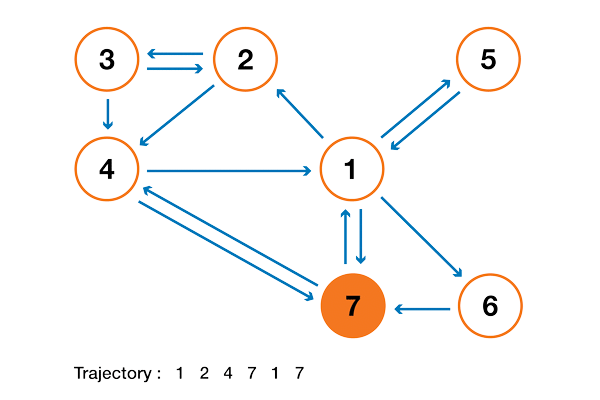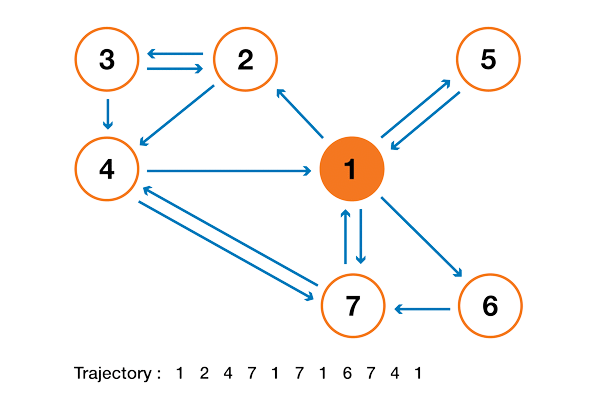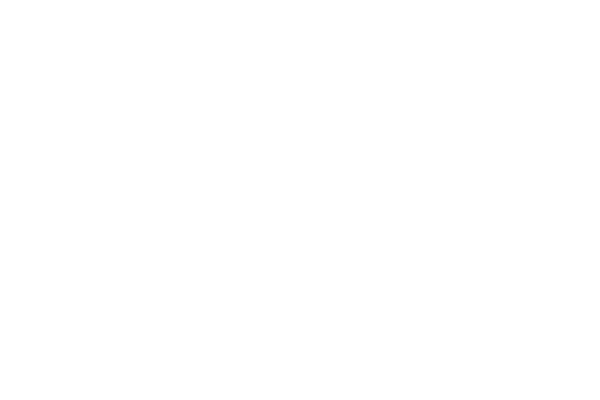
To make this a lot clearer, let's look at an artificial example. Suppose we have a tiny website with 7 pages, labeled 1 to 7, and the links between these pages correspond to the following column.

For the sake of clarity, the probabilities of each transition in the animation shown above are not shown. However, since it is assumed that “navigation” should be exclusively random (this is called “random walk”), the values can be easily reproduced from the following simple rule: for a site with K outgoing links (a page with K links to other pages), the probability of each outgoing link equal to 1 / K. That is, the transition probability matrix has the form:
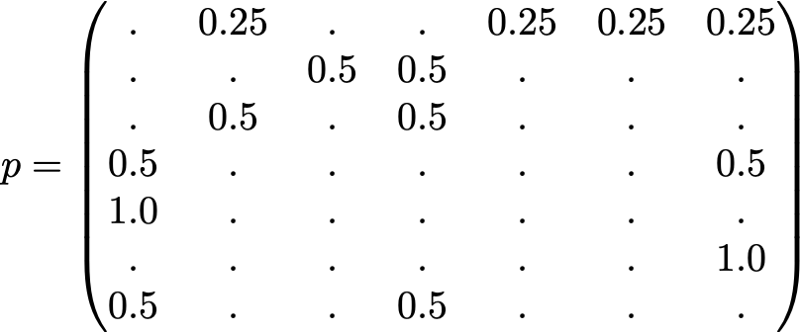
where the values of 0.0 are replaced for convenience by ".". Before performing further calculations, we can notice that this Markov chain is indecomposable and aperiodic, that is, in the long run the system converges to a stationary distribution. As we have seen, this stationary distribution can be calculated by solving the following left eigenvector problem

By doing so, we get the following PageRank values (stationary distribution values) for each page
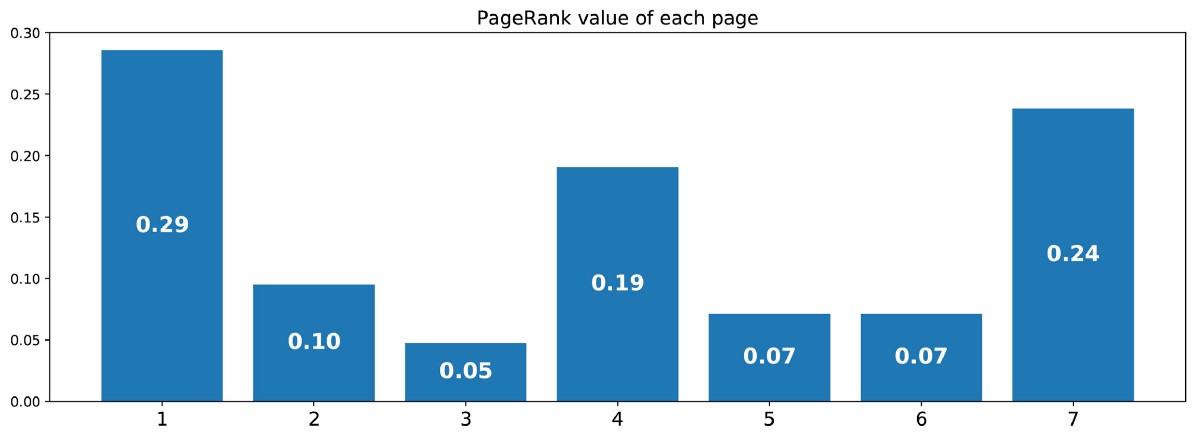
PageRank values calculated for our artificial example of 7 pages.
Then the PageRank ranking of this tiny website is 1> 7> 4> 2> 5 = 6> 3.
conclusions
Key findings from this article:
- random processes are sets of random variables that are often indexed by time (indices often indicate discrete or continuous time)
- for a random process, the Markov property means that for a given current, the probability of the future does not depend on the past (this property is also called “lack of memory”)
- discrete-time Markov chain is random processes with discrete-time indices satisfying the Markov property
- марковское свойство цепей Маркова сильно облегчает изучение этих процессов и позволяет вывести различные интересные явные результаты (среднее время возвратности, стационарное распределение…)
- одна из возможных интерпретаций PageRank (не единственная) заключается в имитации веб-пользователя, случайным образом перемещающегося от страницы к странице; при этом показателем ранжирования становится индуцированное стационарное распределение страниц (грубо говоря, на самые посещаемые страницы в устоявшемся состоянии должны ссылаться другие часто посещаемые страницы, а значит, самые посещаемые должны быть наиболее релевантными)
In conclusion, we emphasize once again how powerful a tool are Markov chains in modeling problems associated with random dynamics. Due to their good properties, they are used in various fields, for example, in queuing theory (optimizing the performance of telecommunication networks, in which messages often have to compete for limited resources and are queued when all resources are already taken), in statistics (well-known Monte Carlo according to the Markov chain scheme for generating random variables is based on Markov chains), in biology (modeling the evolution of biological populations), in computer science (hidden Markov models are important tools umentami in information theory, and speech recognition), as well as in other areas.
Of course, the enormous opportunities provided by Markov chains from the point of view of modeling and computation are much wider than those considered in this modest review. Therefore, we hope that we were able to arouse the reader's interest in further studying these tools, which occupy an important place in the arsenal of a scientist and data expert.
