Neural network architecture for the implementation of the RL algorithm with the ability to specify simultaneously running actions
One of the classic neural network schemes for implementing the RL algorithm is as follows:
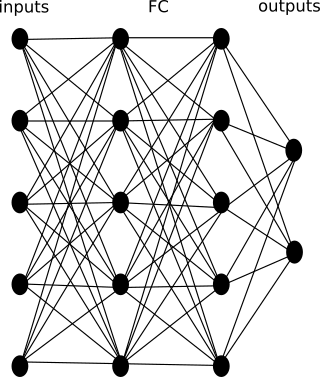
Where: inputs - inputs to the neural network; FC - (fully connected) hidden layer architecture or CNN - FC - architecture hidden layer architecture (depending on what is fed to the inputs); outputs - network outputs. Often, network outputs are a softmax layer that gives the probability of one of the actions from the set of all possible actions.
The disadvantage of this architecture is that it is difficult to implement the choice of several simultaneously performed actions.
To solve this problem, an architecture with a mask layer is proposed. The proposed architecture is as follows:

This architecture is fully consistent with the classical architecture, but also includes an action mask layer. There is only one way out of this architecture - this is the value of the value of the action (a group of simultaneously performed actions). The action mask layer can be implemented in accordance with the pseudo-code below:
And using this code demonstrates the following code snippet:
It can be seen from the layer code that for each action the neural network learns to form some representation of the action as a series of weights. And these representations either go to the network after the mask layer or not. Depending on the operation, these weights can take place with the task of some operation on the entire group of action weights (not only multiplication by [0,1]). Thus, the task of actions is formed to calculate the value of the group of actions performed by the network. (In the classical case, the softmax layer calculated the value of all actions; in the proposed architecture, the neural network calculates the value of a group of selected actions.)
(For example, see R.S. Sutton, E.G. Barto, Reinforcement Learning.)
The idea of using this architecture for playing tetris is as follows. At the inputs we submit the image of the glass of the tetris game (one pixel one square). We group individual actions into action groups. Assessment of one action for a neural network is a mask of the final position of a figure in a glass. The figure is defined by its squares in the action mask in the layer of the action mask in the neural network. To select a group of actions, we select the maximum assessment of the action (exit) from the list of all end positions of the current figure.

Picture. The field (blue cells) and the falling shape (light gray cells) are shown. The final position of the figure is all possible positions from which the figure cannot move according to the rules of the game (not shown).
In this case, each acceleration action (several acceleration accelerations), braking (several possible accelerations during braking), as well as several degrees of rotation were modeled as elementary actions. It is understood that at the same time a rotation and one of the accelerations may be involved, or only one rotation action or one acceleration action. In this case, the architecture allows you to specify several elementary actions at the same time to form a complex action.

Picture. In addition to the field for performing actions by the car model (on which the parking goal is indicated by red and green lines), the inputs of the neural network (below) and the values of the action assessment for all possible actions in this state of the model are also displayed.
Similarly, with the use of tetris in a game, the architecture can be used for other games, where a series of figures and several actions can be specified on the field at the same time (for example, moving around the playing field).
In robotics, this architecture can serve as a meta-network coordinating individual structural elements into a common ensemble.
Also, this architecture allows you to use transfer learning to pre-train the CNN part, and vice versa at the beginning to train the RL part of the neural network, and then train the CNN part on the already trained RL network on model data. In the example, when programming the Tetris game, transfer learning was applied with training at the beginning of the CNN part and the FC part to the action mask layer (what is transferred to the resulting network). In the parking task, I plan to apply CNN training after learning the RL part (ie, the first cherry).
→ Program source code examples can be found here

Where: inputs - inputs to the neural network; FC - (fully connected) hidden layer architecture or CNN - FC - architecture hidden layer architecture (depending on what is fed to the inputs); outputs - network outputs. Often, network outputs are a softmax layer that gives the probability of one of the actions from the set of all possible actions.
The disadvantage of this architecture is that it is difficult to implement the choice of several simultaneously performed actions.
To solve this problem, an architecture with a mask layer is proposed. The proposed architecture is as follows:

This architecture is fully consistent with the classical architecture, but also includes an action mask layer. There is only one way out of this architecture - this is the value of the value of the action (a group of simultaneously performed actions). The action mask layer can be implemented in accordance with the pseudo-code below:
import numpy as np
classLayer:def__init__(self, items, item_size, extra_size):assert(items > 0)
assert(item_size > 0)
assert(extra_size >= 0)
self.items = items
self.item_size = item_size
self.extra_size = extra_size
defbuild(self):
self._expand_op = np.zeros((self.items, self.items*self.item_size), \
dtype=np.float32)
for i in range(self.items):
self._expand_op[i,i*self.item_size:(i+1)*self.item_size] = np.float32(1.0)
defcall(self, inputs, ops):
op_mask_part = inputs[:self.items*self.item_size]
if self.extra_size > 0:
ext_part = inputs[self.items*self.item_size:]
else:
ext_part = None# if ops in [-0.5, 0.5] or [-0.5 .. 0.5]:
ops1 = np.add(ops, np.float(0.5)) # optional
extended_op = np.matmul(ops1, self._expand_op)
if self.extra_size > 0:
return np.concatenate((np.multiply(op_mask_part, extended_op), ext_part))
else:
return np.multiply(op_mask_part,extended_op)
And using this code demonstrates the following code snippet:
items = 5
item_size = 10
extra_size = 20
l = Layer(items=items, item_size=item_size, extra_size=extra_size)
l.build()
inputs = np.random.rand(items*item_size+extra_size)
ops = np.random.randint(0, 2, (items,), dtype="int")
ops = ops.astype(dtype=np.float32) - np.float32(0.5)
result = l.call(inputs,ops)
It can be seen from the layer code that for each action the neural network learns to form some representation of the action as a series of weights. And these representations either go to the network after the mask layer or not. Depending on the operation, these weights can take place with the task of some operation on the entire group of action weights (not only multiplication by [0,1]). Thus, the task of actions is formed to calculate the value of the group of actions performed by the network. (In the classical case, the softmax layer calculated the value of all actions; in the proposed architecture, the neural network calculates the value of a group of selected actions.)
(For example, see R.S. Sutton, E.G. Barto, Reinforcement Learning.)
Examples of using the proposed architecture
Tetris game
The idea of using this architecture for playing tetris is as follows. At the inputs we submit the image of the glass of the tetris game (one pixel one square). We group individual actions into action groups. Assessment of one action for a neural network is a mask of the final position of a figure in a glass. The figure is defined by its squares in the action mask in the layer of the action mask in the neural network. To select a group of actions, we select the maximum assessment of the action (exit) from the list of all end positions of the current figure.

Picture. The field (blue cells) and the falling shape (light gray cells) are shown. The final position of the figure is all possible positions from which the figure cannot move according to the rules of the game (not shown).
Agent simulating the movement of a car
In this case, each acceleration action (several acceleration accelerations), braking (several possible accelerations during braking), as well as several degrees of rotation were modeled as elementary actions. It is understood that at the same time a rotation and one of the accelerations may be involved, or only one rotation action or one acceleration action. In this case, the architecture allows you to specify several elementary actions at the same time to form a complex action.

Picture. In addition to the field for performing actions by the car model (on which the parking goal is indicated by red and green lines), the inputs of the neural network (below) and the values of the action assessment for all possible actions in this state of the model are also displayed.
Other possible applications of architecture
Similarly, with the use of tetris in a game, the architecture can be used for other games, where a series of figures and several actions can be specified on the field at the same time (for example, moving around the playing field).
In robotics, this architecture can serve as a meta-network coordinating individual structural elements into a common ensemble.
Also, this architecture allows you to use transfer learning to pre-train the CNN part, and vice versa at the beginning to train the RL part of the neural network, and then train the CNN part on the already trained RL network on model data. In the example, when programming the Tetris game, transfer learning was applied with training at the beginning of the CNN part and the FC part to the action mask layer (what is transferred to the resulting network). In the parking task, I plan to apply CNN training after learning the RL part (ie, the first cherry).
→ Program source code examples can be found here
