The most beautiful theorem of mathematics: Euler's identity
- Transfer
After watching a lecture by Professor Robin Wilson on Euler identity, I was finally able to understand why Euler identity is the most beautiful equation. To share my admiration for this topic and to strengthen my own knowledge, I will outline the notes made during the lecture. And here you can buy his wonderful book.
What could be more mysterious than the interaction of imaginary numbers with real numbers, resulting in nothing? Such a question was asked by a reader of Physics World magazine in 2004 to emphasize the beauty of the Euler equation "e in degree i times pi is minus one . "
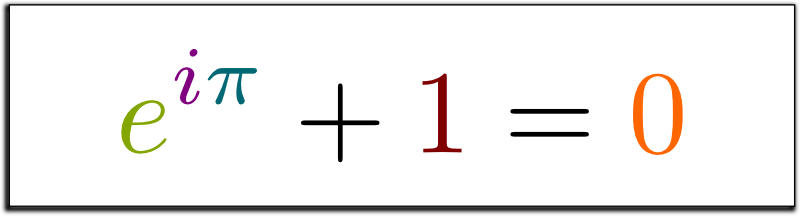
Figure 1.0 : Euler identity - e in degree i times pi, plus one is zero.
Earlier, in 1988, the mathematician David Wells, who wrote articles for the American mathematical journal The Mathematical Intelligencer , compiled a list of 24 mathematical theorems and conducted a survey asking readers of his article to choose the most beautiful theorem. And after Euler's equation won by a wide margin in it, it received the title of "the most beautiful equation in mathematics."

Figure 2.0 : The Mathematical Intelligencer magazine cover

Figure 3.0 : A survey by David Wells from
Leonard Euler magazine is called the most productive mathematician in history. Other outstanding mathematicians were inspired by his work. One of the best physicists in the world, Richard Feynman, in his famous lectures on physics, called the Euler equation "the most remarkable formula in mathematics . " Another terrific mathematician, Michael Atiyah, called this formula "... the mathematical counterpart of Hamlet’s phrase" to be or not to be "- very short, very concise, and at the same time very deep . "
There are many interesting facts about the Euler equation. For example, it was found in some episodes of The Simpsons.

Figure 4.0 : In this scene, the Euler equation can be seen on the second book in the rightmost stack.

Figure 5.0 : In this scene, the Euler equation is written on a T-shirt of a secondary character.
Also, the Euler equation has become a key point in the criminal case . In 2003, graduate student at the California Institute of Technology Billy Cottrell painted Euler's equation on other people's sports cars. At the trial, he said: “ I have known Euler’s theorem since I was five, and everyone must know it .”

Figure 6.0 : A stamp issued in 1983 in Germany commemorating the bicentenary of the death of Euler.

Figure 7.0 : A stamp issued by Switzerland in 1957 in honor of Euler’s 250th anniversary.
You have every right to wonder: why did Billy Cottrell think that everyone should know about the Euler equation? And was so sure of this that he began to write it on other people's machines? The answer is simple: Euler used the three fundamental constants of mathematics and applied the mathematical operations of multiplication and exponentiation to write a beautiful formula, resulting in zero or minus one.
Euler's identity first appeared in 1748 in his book Introductio in analysin infinitorum . Later, other people saw that this formula is related to the trigonometric functions of the sine and cosine, and this connection is surprising, because the power function tends to infinity, and the trigonometric functions range from -1 to -1.
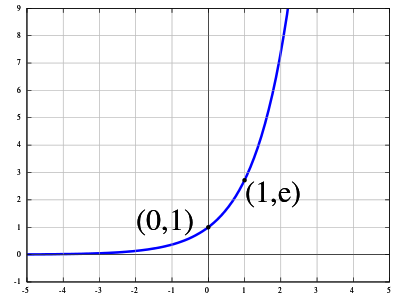
Figure 8.0 : exponential function y = e x .
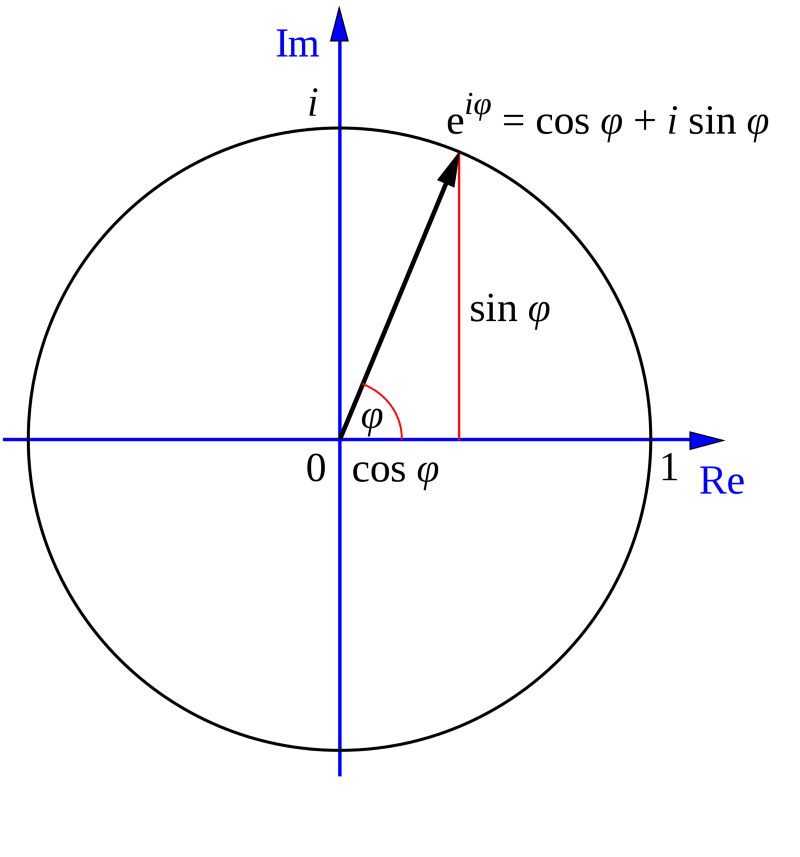
Figure 8.1 : Euler identity graph.
Figure 8.2 : Frequencies emitted by the LC circuit.
The equations and graphs shown above may seem abstract, but they are important for quantum physics and image processing calculations, and at the same time depend on Euler's identity.
The number 1 (unit) is the foundation of our calculus system. With her we begin to count. But what do we think? To count, we use the digits 0–9 and a system of digits that determines the value of the digit.
For example, the number 323 means 3 hundreds, 2 tens and 3 units. Here, the number 3 plays two different roles, which depend on its location.
323 = (3 * 100) + (2 * 10) + (3 * 1)
There is another system of calculus, called binary. In this system, base 2 is used instead of 10. It is widely used in computers and programming. For example, in a binary system:
1001 = (2 3 ) + (0 2 ) + (0 1 ) + (2 0 ) = [9 in a base 10 system]
Who created the calculus system? How did the first people count objects or animals?
How did our calculus systems come about? What did the first civilizations think? We know for sure that they did not use our bit system. For example, 4000 years ago, the ancient Egyptians used a number system with different symbols. However, they combined the characters to create a new character for numbers.

Figure 11 : the hieroglyphs shown here form the number 4622; this is one of the numbers carved on the wall in the temple in Karnak (Egypt).

Figure 12 : Hieroglyphs are images representing words, and in this case, numbers.
At the same time, but in another place, another society discovered a method of counting, but symbols were also used in it. In addition, the basis of their calculus was 60, not 10. We use their counting method to determine the time; therefore, 60 minutes in a minute, and 60 minutes in an hour.

Figure 13 : Babylonian numbers from a hexadecimal number system (with base 60).
A thousand years later, the ancient Romans invented Roman numbers. They used letters to indicate numbers. The Roman notation is not considered a bit system, because for many values of our number system, different letters were used in it. It is for this reason that they used an abacus for counting.

Figure 14 : Roman abacus in hexadecimal (with base 16) number system

Figure 15 : conversion table from Arabic to Roman numbers
The ancient Greeks also did not use the digit system. Greek mathematicians denoted numbers by letters. They had special letters for numbers from 100 to 900. Many people at the time considered Greek numbers to be confusing.
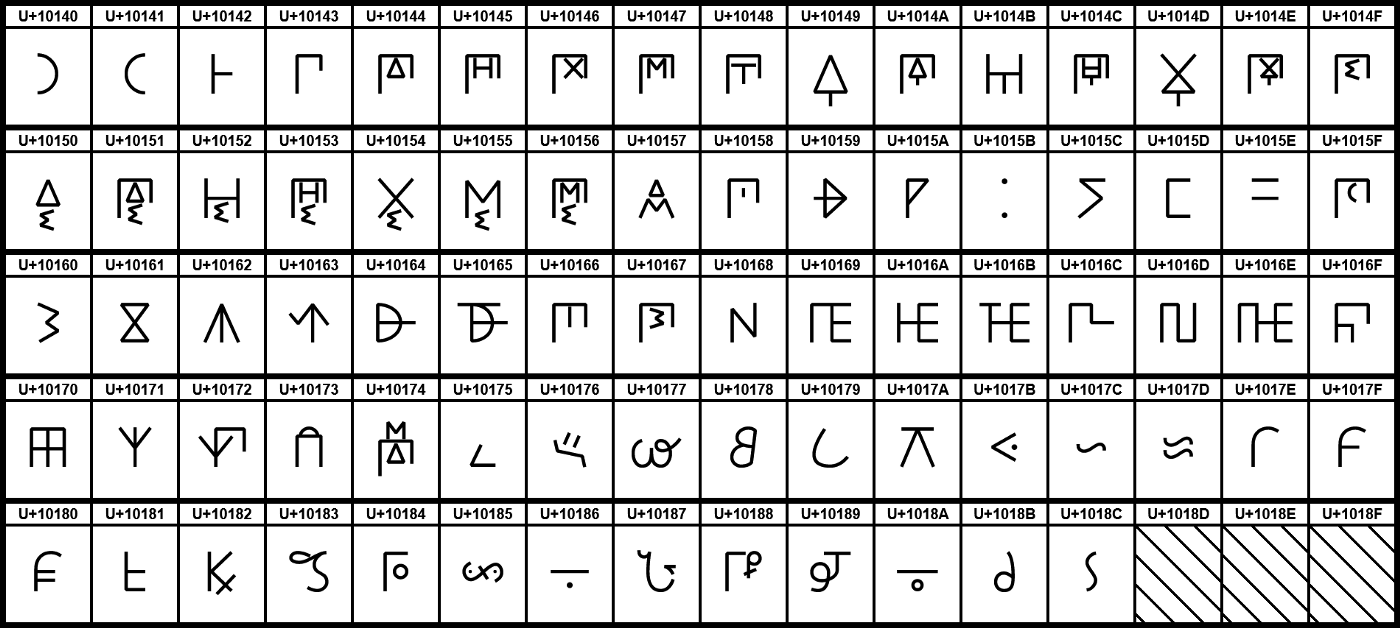
Figure 15 : Ancient Greek letter table.
At the same time, Chinese mathematicians began to use small bamboo sticks for calculations. This Chinese counting method is called the first decimal place system.

Figure 16 : Chinese way of counting with stick numbers. Used at least from 400 BC. The square counting board was used until about 1500, when it was replaced by an abacus.
However, the most unique account system was used by the Maya Indians. Their number system had a base of 20. To indicate numbers from 1 to 19, they used dots and lines. What was the difference between their number system? For each number they used head images and a separate zero symbol 0.
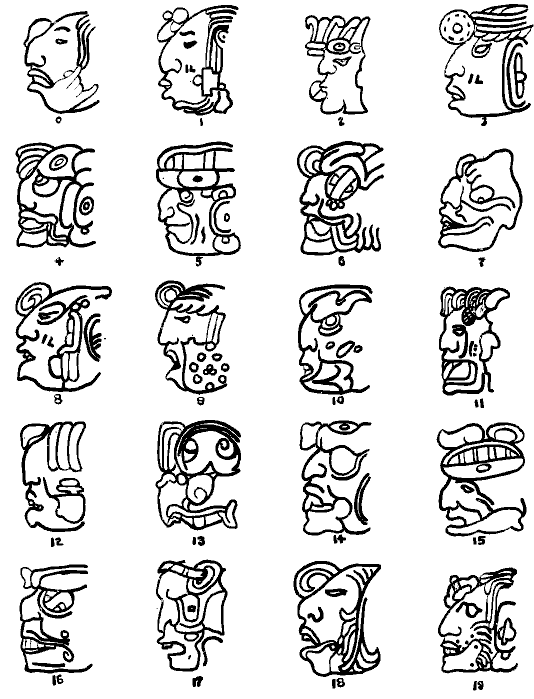
Figure 17: The Mayan number system with base 20, in which numbers are indicated by heads

Figure 18 : Another way to write Mayan numbers.
Some civilizations used spaces to, for example, distinguish the number 101 from 11. After some time, a special number began to appear - zero. For example, in a cave in the Indian city of Gwalior, archaeologists found on the wall the number 270, in which there was zero. The very first recorded use of zero can be seen in the Bodleian library.

Figure 19 : The circle carved on the wall of the temple in Gwalior denotes zero. He is about 1,500 years old.

Figure 20 : black dots in the Bakhshali manuscript indicate zeros; this is the oldest written example of the use of numbers, it is about 1800 years old.
About 1400 years ago, the rules for computing with zero were written. For example, adding a negative number and zero produces the same negative number. Division by zero is not allowed, because if divided by zero, we get a number that can be equal to any number we need, which should be prohibited.
Soon after, many people published books on arithmetic that spread the use of Indo-Arabic notation of numbers. Below is the evolution of Indo-Arabic numbers. Most countries use the Indo-Arabic number system, but Arab countries still use Arabic numbers.
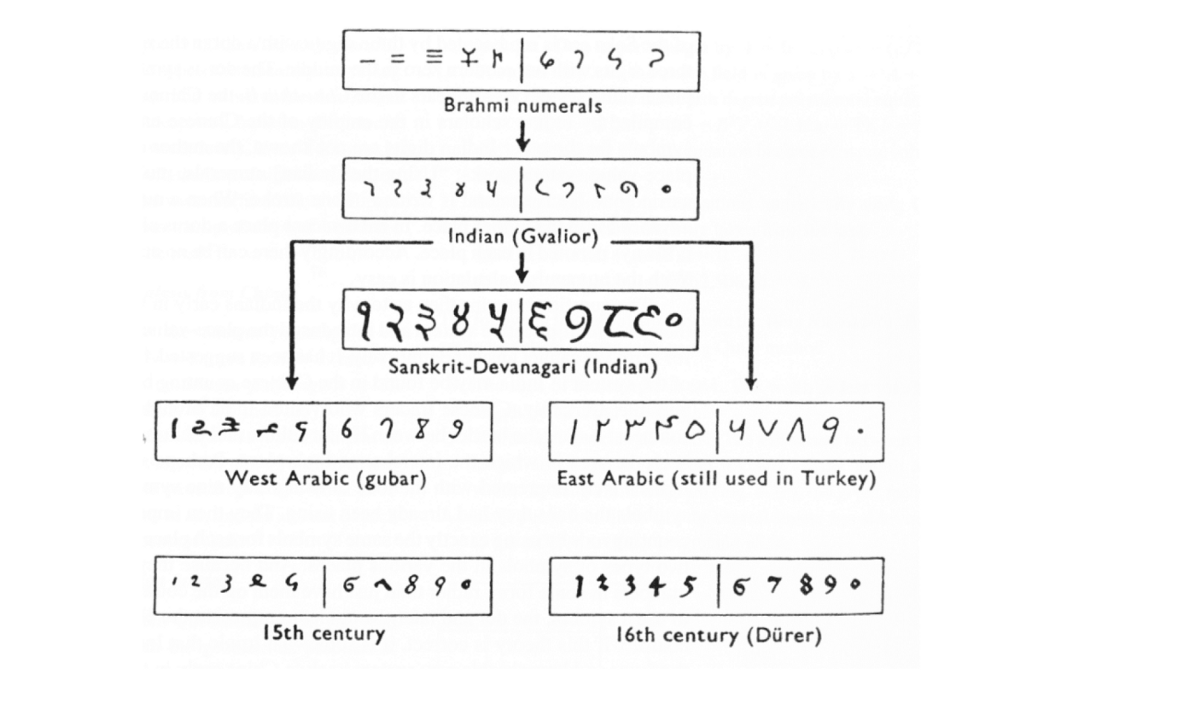
Figure 21 : This diagram shows the evolution of numbers, originating from Brahmi numbers and ending with the numbers that we use today.

Figure 22 : A classic engraving "Arithmetic" from Gregor Reish 's Margarita Philosophica , which depicts a competition between Boethius, smiling after discovering Indo-Arabic numbers and written calculations, and the frowning Pythagoras, still trying to use a number board.
Pi is the most popular irrational number known to us. Pi can be found in two ways: by calculating the ratio of the circumference of a circle to its diameter, or the ratio of the area of a circle to the square of its radius. Euclid proved that these relations are constant for all circles, even for the moon, penny, tire, etc.
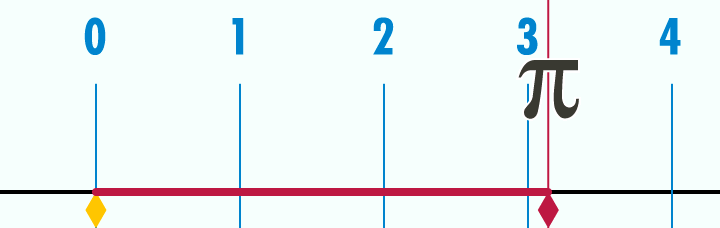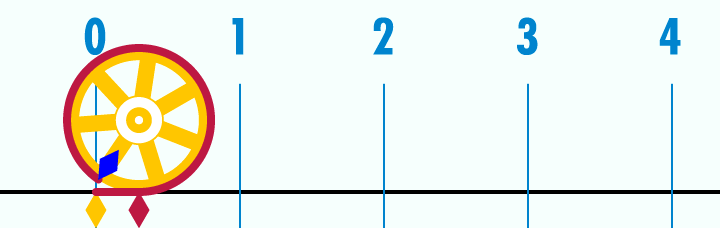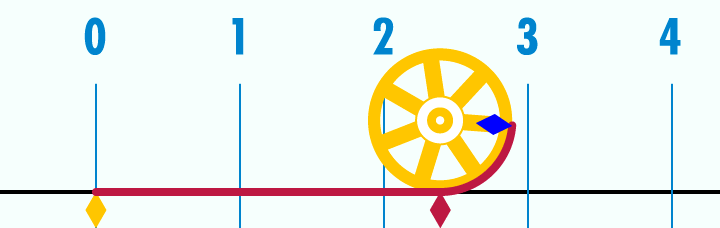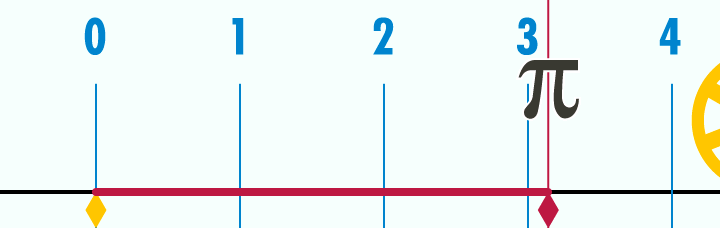
Figure 22 : Animated relationship between circle and diameter in relation to pi.
Since irrational numbers like pi are infinite and have no repetition, we will never finish writing pi. It goes on forever. There are people who remember many decimal places pi (the current record is 70,000 digits! Source: Guinness Book of Records ).
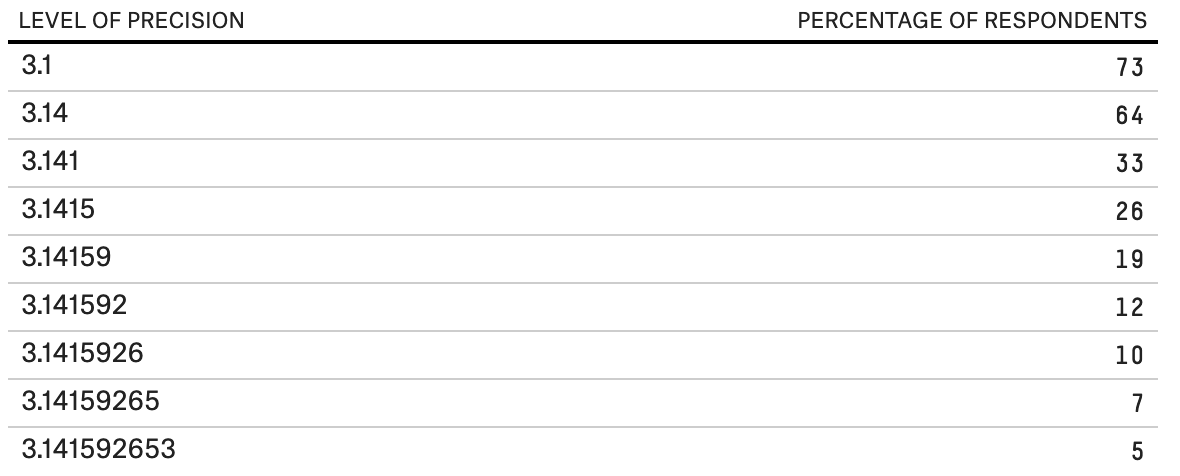
Figure 23 : Survey data of 941 respondents to determine the percentage of people who can remember pi characters after the decimal point.

Figure 24 : Hundreds of pi discharges are recorded on the wall of the Karlsplatz metro station in Vienna.
Currently, computers have been able to calculate a total of 2.7 trillion pi bits. It may seem like a lot, but in fact this path is endless.
As I said above, the number pi found Euclid. But what did people do before Euclid when they needed to find the area of a circle? Historians have discovered a Babylonian clay tablet, in which the ratio of the perimeter of the hexagon to the diameter of the circle described around it was recorded. After calculations, the resulting number turned out to be 3.125. It is very close to pi.

Figure 24 : Babylonian clay tablet with the ratio of the perimeter of the hexagon to the length of the circumscribed circle.

Figure 25 : Numberwarrior
Ancient Egyptians also came close to pi. Historians have discovered a document showing how the ancient Egyptians found the number pi. When historians translated the document, they found the following task:


Figure 26 : Achmes' mathematical papyrus .
Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.
A thousand years later, the German mathematician Ludolf Zeilen worked with 2 62- sided polygons and received 35 decimal digits pi. This number, called Lyudolfov, was carved on his gravestone.



In 1706, the Englishman John Machin, who had long been a professor of astronomy, used the addition formula to prove that pi equals
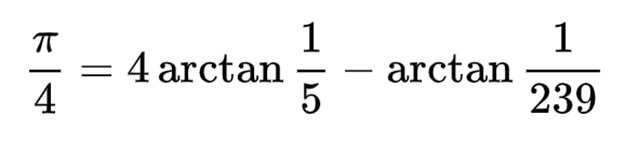
Not worried about where this formula came from, Macin began to use it constantly, and then wrote down the series shown below. This was the largest step at that time in the number of digits pi.

Figure 29 : Machin's formula for pi.
However, the first mention of pi appeared in 1706. Mathematics teacher William Jones wrote a book and first proposed pi for measuring circles. So pi first appeared in books!



Figure 30 : Juliabloggers
In 1873, William Shanks used the John Machin formula and received 707 decimal digits. These numbers are written in the room of the Paris Palace of Discoveries. However, later mathematicians found that only 527 digits were true.

Figure 31 : pi room
On the other hand, Buffon discovered a more interesting way of finding pi. His experiment was based on randomly scattering needles to evaluate pi. He drew several parallel lines on the board at a distance D and took needles of length L. Then he randomly started throwing needles on the board and wrote down the proportion of needles crossing the line.

Figure 32.0 : Science Friday
And after that, another mathematician named Lazzarini threw a needle 3408 times and received six decimal digits pi with a ratio of 355/113. However, if one needle did not cross the line, he would receive only 2 digits pi.
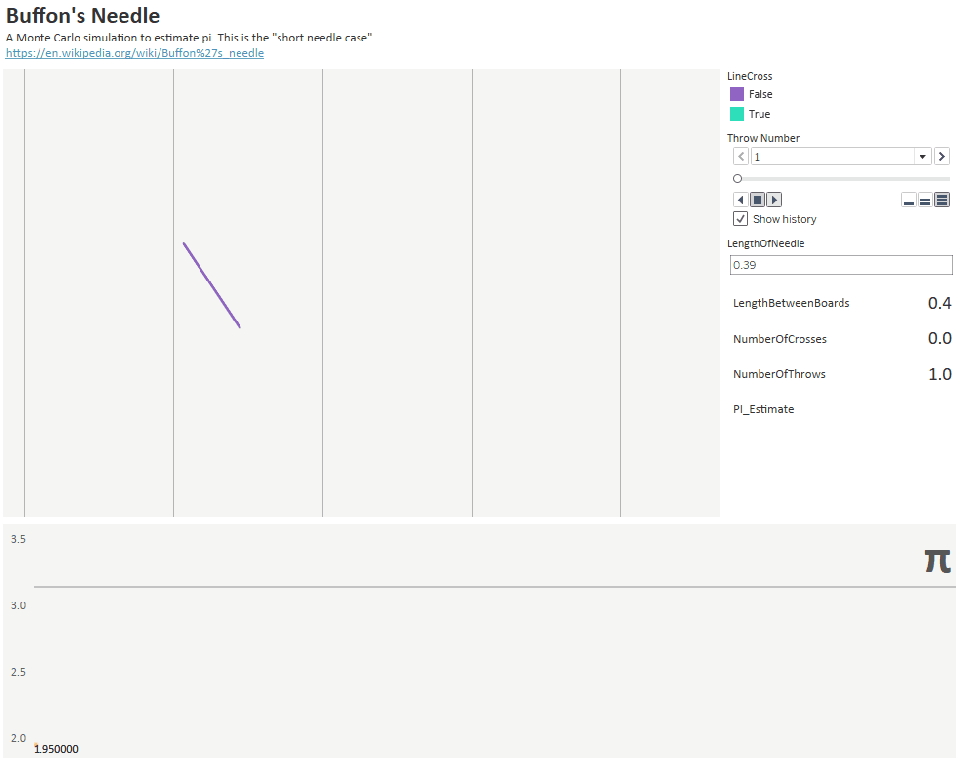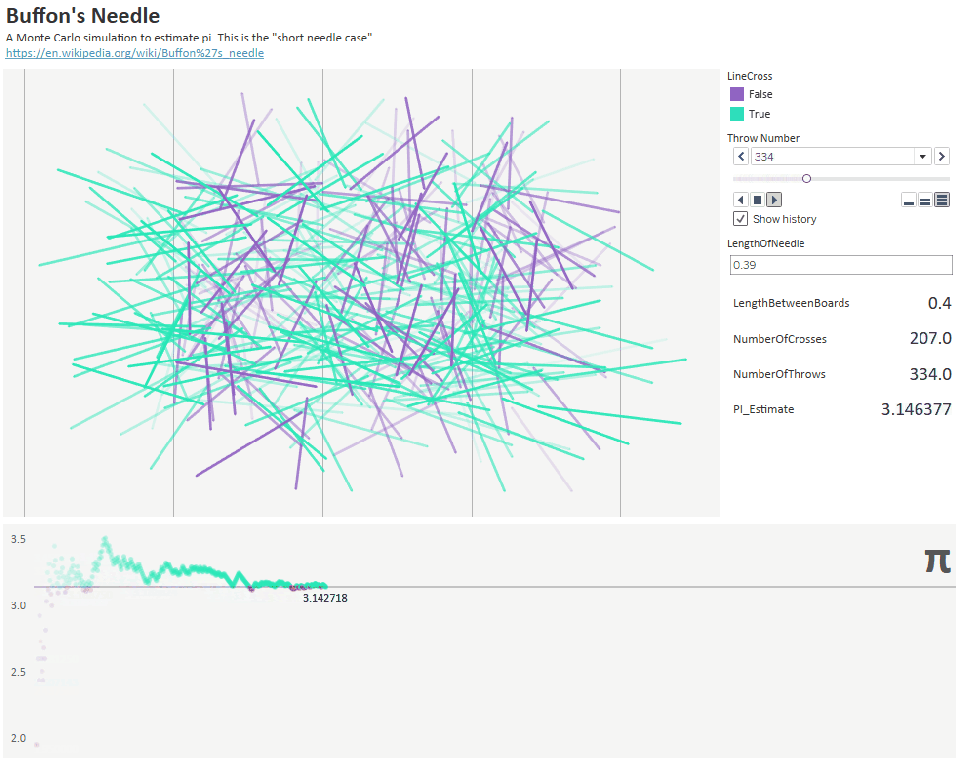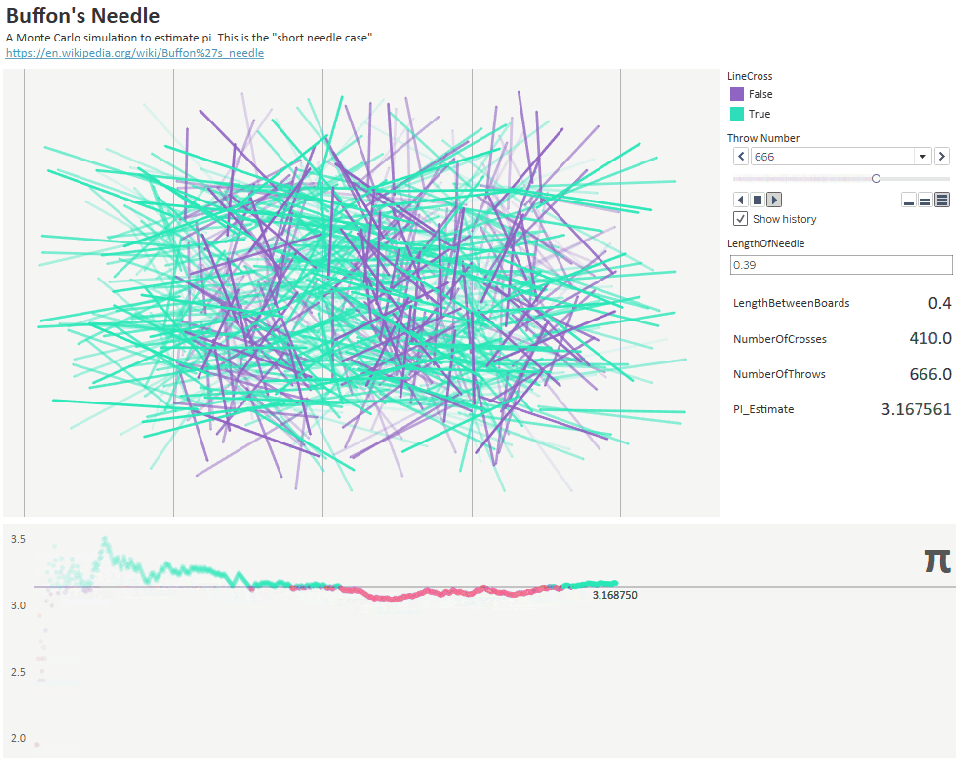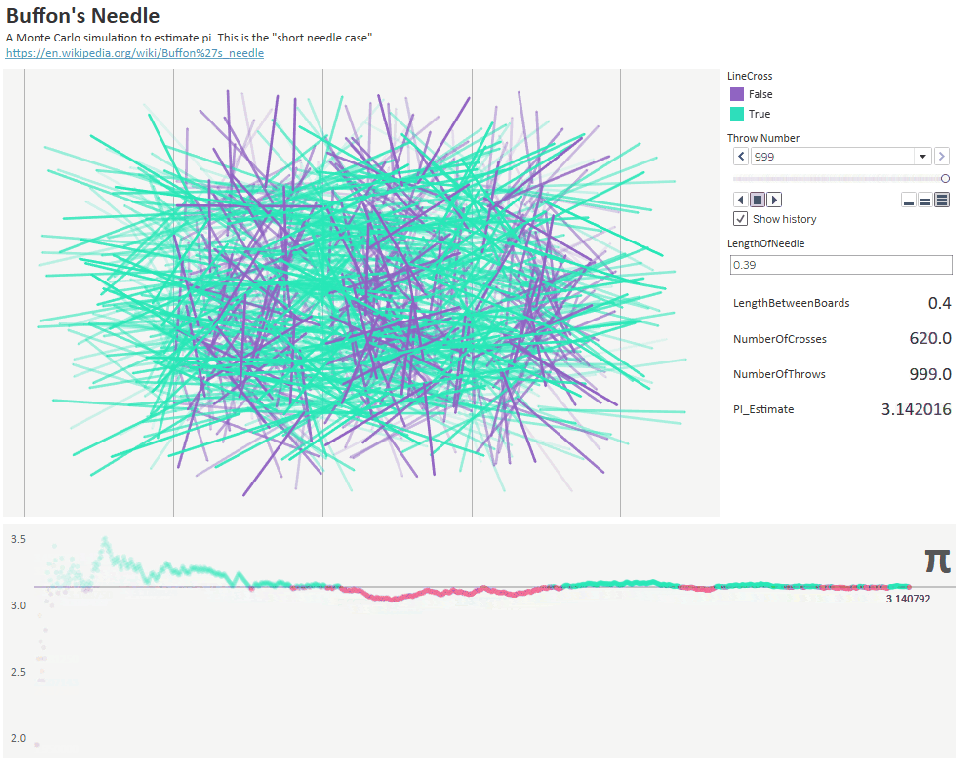
Figure 32.1 : Throwing 1000 needles to estimate the approximate pi
e is another famous irrational number. The fractional part e is also infinite, like pi. We use the number e to calculate power (exponential) growth. In other words, we use e when we see very fast growth or decrease.
One of the greatest, and perhaps the best mathematician, Leonard Euler discovered the number e in 1736 and first mentioned this special number in his book Mechanica .


Figure 33 : source
To understand exponential growth, we can use the story of a chess inventor. When he came up with this game, he showed it to the ruler of the North. The king liked the game and he promised that he would give the author any reward. Then the inventor asked for something very simple: 2 0 grains per first cell of a chessboard, 2 1 grains per second cell of a board, 2 2 grains per third, and so on. Each time, the amount of grain doubled. The king of the North thought that the request would be easy to fulfill, but he was mistaken, because it would be necessary to put 2 63 grainson the last cell, which is 9 223 372 036 854 775 808. This is exponential growth. It started at 1, doubled constantly, and after 64 steps it grew into a huge number!
If a chess inventor chose a linear equation, for example, 2n, he would get 2, 4, 6, 8, ... 128 ... Therefore, in the long run, exponential growth often far exceeds polynomial.

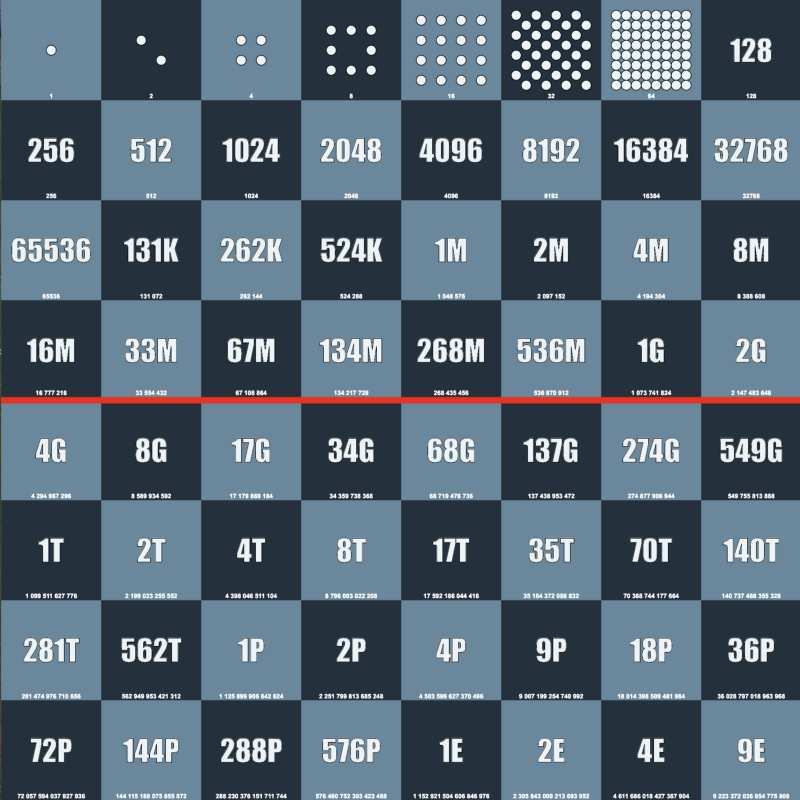
Figure 34 : source: Wikipedia
The number e was discovered by Euler. However, Jacob Bernoulli also worked with the number ewhen calculating compound interest to earn more money. If you invest $ 100 at 10% of the income, how will this amount grow? Firstly, it depends on how often the bank calculates interest. For example, if he calculates once, then we will receive $ 110 at the end of the year. If we change our minds and take interest every 6 months, then in this case we will receive more than 110 dollars. The fact is that the percentage received in the first 6 months will also receive its percentage. The total amount will be equal to 110.25 dollars. You can guess that we can get more money if we take money every quarter of the year. And if we make the time interval shorter, the final amounts will continue to grow. Such an infinite compound interest will make us rich! However, our total revenue tends to a limited value associated withe .
Bernoulli did not call the number 2.71828 by the name e . When Euler worked with 2.71828, he raised the exponential function e to the power of x . He outlined his discoveries in the book The Analysis of Infinite .
In 1798, Thomas Malthus used an exponential function in his essay on the nutritional deficiency of the future. He created a line graph showing food production and an exponential graph showing the world's population. Malthus concluded that in the long run, exponential growth will triumph, and the world is facing a serious food shortage. This phenomenon was called the "Malthusian catastrophe." Newton also used this model to show how a cup of tea cools.
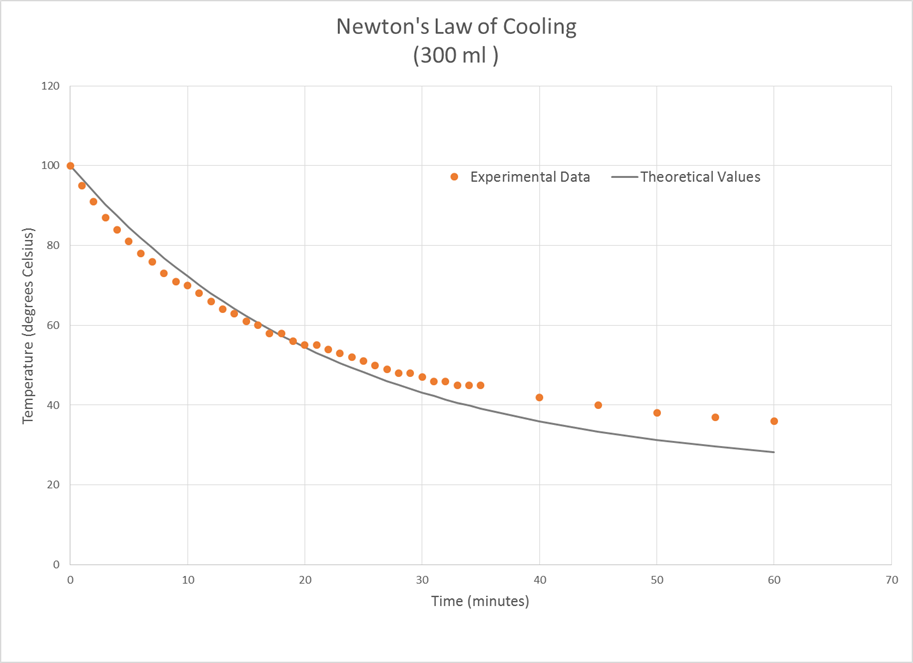
Figure 35 : Newton-Richmann law
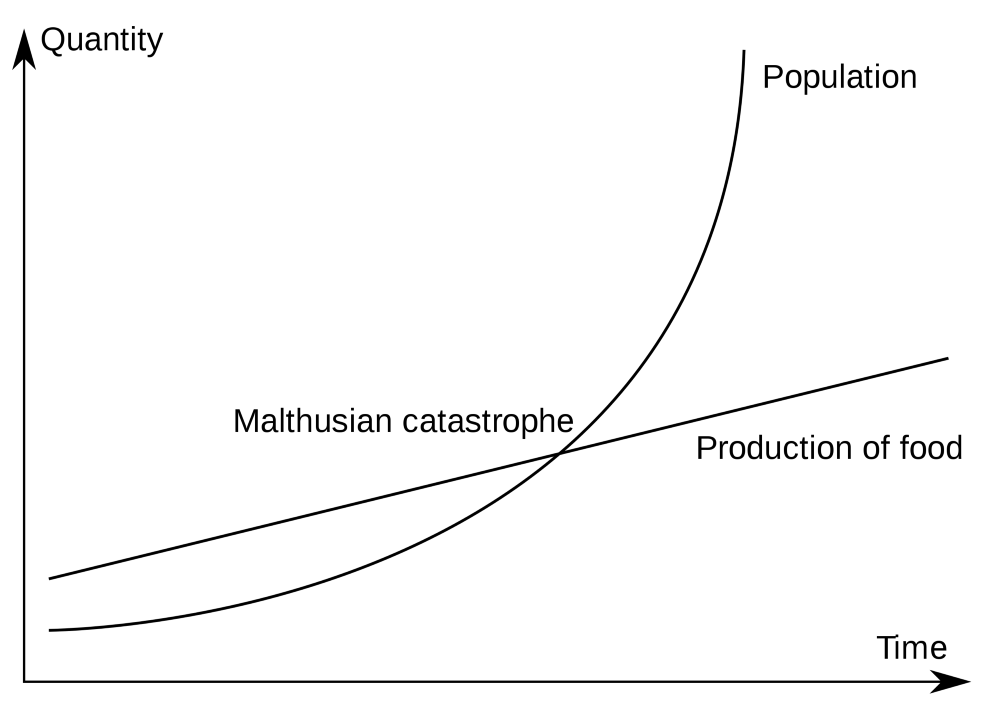
Рисунок 36: мальтузианская катастрофа
For a long time, mathematicians had enough ordinary numbers to solve their problems. However, at some point for their further development they needed to discover something new and mysterious. For example, the Italian mathematician Cardano tried to divide the number 10 into 2 parts, the product of which would be equal to 40. To solve this problem, he wrote down the equation: x (10-x) = 40. When he solved this quadratic equation, he got two solutions: 5 plus √-15 and 5 minus √-15, which at that time did not make any sense. This result was meaningless, because by the definition of the square root he needed to find a number whose square would be negative. However, both positive and negative numbers squared have a positive value. Be that as it may, he found his unique number. However, the first mathematiciani was Euler.
Leibniz gave such a comment about the imaginary number √-1:
We can add, subtract, multiply and divide imaginary numbers. Addition, subtraction and multiplication are simple, and division is a little more complicated. The real and imaginary parts are folded separately. In the case of multiplication, i 2 will be equal to -1.
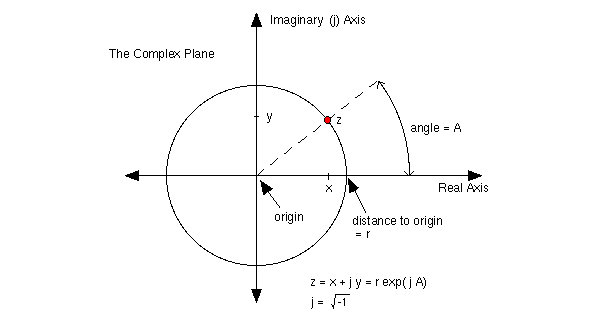
After Euler, mathematician Caspar Wessel introduced imaginary numbers geometrically and created a complex plane. Today we represent each complex number a + bi as a point with coordinates (a, b).
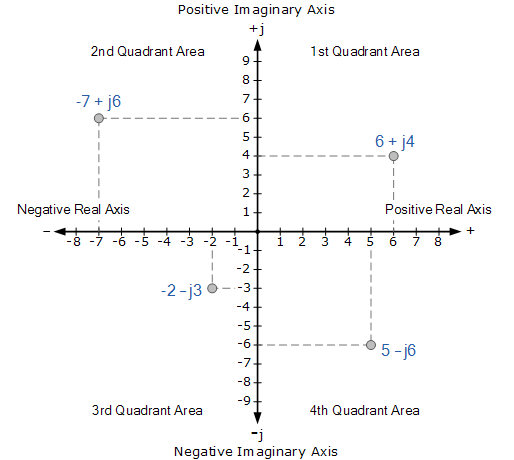
Figures 37 and 38 : complex numbers
In the Victorian era, many were suspicious of imaginary numbers. However, the Irish mathematician and astronomer William Rowan Hamilton ended these doubts by defining complex numbers as applied to quaternions .
Euler's identity connects an exponential function with sine and cosine functions, whose values range from minus one to one. To find a connection with trigonometric functions, we can represent them in the form of an infinite series, true for all values
Figure 39 : Discovery of Euler Identity
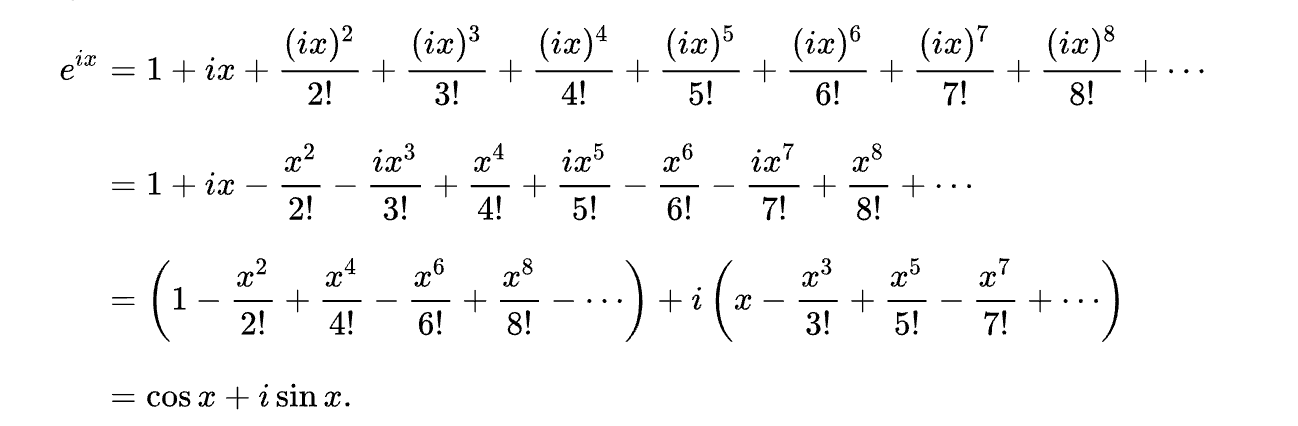
Figure 40 : Euler identity
Euler has never recorded this identity explicitly, and we do not know who first recorded it. Nevertheless, we associate it with the name of Euler in deference to this great pioneer of mathematics.
What could be more mysterious than the interaction of imaginary numbers with real numbers, resulting in nothing? Such a question was asked by a reader of Physics World magazine in 2004 to emphasize the beauty of the Euler equation "e in degree i times pi is minus one . "
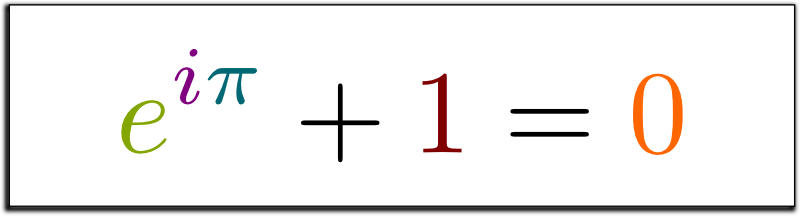
Figure 1.0 : Euler identity - e in degree i times pi, plus one is zero.
Earlier, in 1988, the mathematician David Wells, who wrote articles for the American mathematical journal The Mathematical Intelligencer , compiled a list of 24 mathematical theorems and conducted a survey asking readers of his article to choose the most beautiful theorem. And after Euler's equation won by a wide margin in it, it received the title of "the most beautiful equation in mathematics."

Figure 2.0 : The Mathematical Intelligencer magazine cover

Figure 3.0 : A survey by David Wells from
Leonard Euler magazine is called the most productive mathematician in history. Other outstanding mathematicians were inspired by his work. One of the best physicists in the world, Richard Feynman, in his famous lectures on physics, called the Euler equation "the most remarkable formula in mathematics . " Another terrific mathematician, Michael Atiyah, called this formula "... the mathematical counterpart of Hamlet’s phrase" to be or not to be "- very short, very concise, and at the same time very deep . "
There are many interesting facts about the Euler equation. For example, it was found in some episodes of The Simpsons.

Figure 4.0 : In this scene, the Euler equation can be seen on the second book in the rightmost stack.

Figure 5.0 : In this scene, the Euler equation is written on a T-shirt of a secondary character.
Also, the Euler equation has become a key point in the criminal case . In 2003, graduate student at the California Institute of Technology Billy Cottrell painted Euler's equation on other people's sports cars. At the trial, he said: “ I have known Euler’s theorem since I was five, and everyone must know it .”

Figure 6.0 : A stamp issued in 1983 in Germany commemorating the bicentenary of the death of Euler.

Figure 7.0 : A stamp issued by Switzerland in 1957 in honor of Euler’s 250th anniversary.
Why is the Euler equation so important?
You have every right to wonder: why did Billy Cottrell think that everyone should know about the Euler equation? And was so sure of this that he began to write it on other people's machines? The answer is simple: Euler used the three fundamental constants of mathematics and applied the mathematical operations of multiplication and exponentiation to write a beautiful formula, resulting in zero or minus one.
- The constant e is related to power functions.
- The constant i is not real, but an imaginary number equal to the square root of minus one.
- The famous constant π (pi) is connected with circles.
Euler's identity first appeared in 1748 in his book Introductio in analysin infinitorum . Later, other people saw that this formula is related to the trigonometric functions of the sine and cosine, and this connection is surprising, because the power function tends to infinity, and the trigonometric functions range from -1 to -1.
e to the power of i times ϕ (phi) = cos ϕ + i * sin ϕ

Figure 8.0 : exponential function y = e x .

Figure 8.1 : Euler identity graph.

Figure 8.2 : Frequencies emitted by the LC circuit.
The equations and graphs shown above may seem abstract, but they are important for quantum physics and image processing calculations, and at the same time depend on Euler's identity.
1: number for the account
The number 1 (unit) is the foundation of our calculus system. With her we begin to count. But what do we think? To count, we use the digits 0–9 and a system of digits that determines the value of the digit.
For example, the number 323 means 3 hundreds, 2 tens and 3 units. Here, the number 3 plays two different roles, which depend on its location.
323 = (3 * 100) + (2 * 10) + (3 * 1)
There is another system of calculus, called binary. In this system, base 2 is used instead of 10. It is widely used in computers and programming. For example, in a binary system:
1001 = (2 3 ) + (0 2 ) + (0 1 ) + (2 0 ) = [9 in a base 10 system]
Who created the calculus system? How did the first people count objects or animals?
How did our calculus systems come about? What did the first civilizations think? We know for sure that they did not use our bit system. For example, 4000 years ago, the ancient Egyptians used a number system with different symbols. However, they combined the characters to create a new character for numbers.

Figure 11 : the hieroglyphs shown here form the number 4622; this is one of the numbers carved on the wall in the temple in Karnak (Egypt).

Figure 12 : Hieroglyphs are images representing words, and in this case, numbers.
At the same time, but in another place, another society discovered a method of counting, but symbols were also used in it. In addition, the basis of their calculus was 60, not 10. We use their counting method to determine the time; therefore, 60 minutes in a minute, and 60 minutes in an hour.

Figure 13 : Babylonian numbers from a hexadecimal number system (with base 60).
A thousand years later, the ancient Romans invented Roman numbers. They used letters to indicate numbers. The Roman notation is not considered a bit system, because for many values of our number system, different letters were used in it. It is for this reason that they used an abacus for counting.

Figure 14 : Roman abacus in hexadecimal (with base 16) number system

Figure 15 : conversion table from Arabic to Roman numbers
The ancient Greeks also did not use the digit system. Greek mathematicians denoted numbers by letters. They had special letters for numbers from 100 to 900. Many people at the time considered Greek numbers to be confusing.

Figure 15 : Ancient Greek letter table.
At the same time, Chinese mathematicians began to use small bamboo sticks for calculations. This Chinese counting method is called the first decimal place system.

Figure 16 : Chinese way of counting with stick numbers. Used at least from 400 BC. The square counting board was used until about 1500, when it was replaced by an abacus.
However, the most unique account system was used by the Maya Indians. Their number system had a base of 20. To indicate numbers from 1 to 19, they used dots and lines. What was the difference between their number system? For each number they used head images and a separate zero symbol 0.
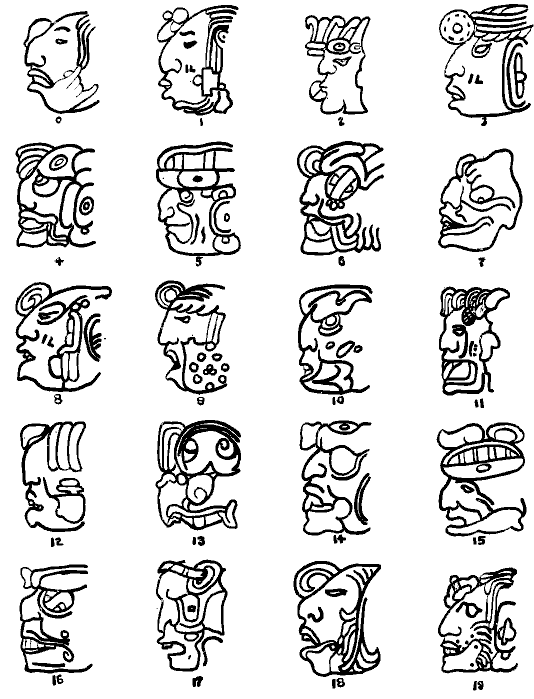
Figure 17: The Mayan number system with base 20, in which numbers are indicated by heads

Figure 18 : Another way to write Mayan numbers.
0: number to indicate nothing
Some civilizations used spaces to, for example, distinguish the number 101 from 11. After some time, a special number began to appear - zero. For example, in a cave in the Indian city of Gwalior, archaeologists found on the wall the number 270, in which there was zero. The very first recorded use of zero can be seen in the Bodleian library.

Figure 19 : The circle carved on the wall of the temple in Gwalior denotes zero. He is about 1,500 years old.

Figure 20 : black dots in the Bakhshali manuscript indicate zeros; this is the oldest written example of the use of numbers, it is about 1800 years old.
About 1400 years ago, the rules for computing with zero were written. For example, adding a negative number and zero produces the same negative number. Division by zero is not allowed, because if divided by zero, we get a number that can be equal to any number we need, which should be prohibited.
Soon after, many people published books on arithmetic that spread the use of Indo-Arabic notation of numbers. Below is the evolution of Indo-Arabic numbers. Most countries use the Indo-Arabic number system, but Arab countries still use Arabic numbers.

Figure 21 : This diagram shows the evolution of numbers, originating from Brahmi numbers and ending with the numbers that we use today.

Figure 22 : A classic engraving "Arithmetic" from Gregor Reish 's Margarita Philosophica , which depicts a competition between Boethius, smiling after discovering Indo-Arabic numbers and written calculations, and the frowning Pythagoras, still trying to use a number board.
Pi (π): the most famous irrational number
Pi is the most popular irrational number known to us. Pi can be found in two ways: by calculating the ratio of the circumference of a circle to its diameter, or the ratio of the area of a circle to the square of its radius. Euclid proved that these relations are constant for all circles, even for the moon, penny, tire, etc.
π = circle / diameter OR π = circle area / radius²

Figure 22 : Animated relationship between circle and diameter in relation to pi.
Since irrational numbers like pi are infinite and have no repetition, we will never finish writing pi. It goes on forever. There are people who remember many decimal places pi (the current record is 70,000 digits! Source: Guinness Book of Records ).

Figure 23 : Survey data of 941 respondents to determine the percentage of people who can remember pi characters after the decimal point.

Figure 24 : Hundreds of pi discharges are recorded on the wall of the Karlsplatz metro station in Vienna.
Currently, computers have been able to calculate a total of 2.7 trillion pi bits. It may seem like a lot, but in fact this path is endless.
As I said above, the number pi found Euclid. But what did people do before Euclid when they needed to find the area of a circle? Historians have discovered a Babylonian clay tablet, in which the ratio of the perimeter of the hexagon to the diameter of the circle described around it was recorded. After calculations, the resulting number turned out to be 3.125. It is very close to pi.

Figure 24 : Babylonian clay tablet with the ratio of the perimeter of the hexagon to the length of the circumscribed circle.

Figure 25 : Numberwarrior
Ancient Egyptians also came close to pi. Historians have discovered a document showing how the ancient Egyptians found the number pi. When historians translated the document, they found the following task:
For example, to find the area of a field with a diameter of 9 hat (1 hat = 52.35 meters), you need to perform the following calculation:
Subtract 1/9 of the diameter, namely 1. The remainder is 8. Multiply it by 8, which gives us 64. Therefore, the area will be 64 setjat (unit of area).
In other words, the diameter is 2r, and 1/9 of the radius is (1/9 • 2r). Then if we subtract this from the initial diameter, then we get 2r - (1/9 • 2r) = 8/9 (2r). Then the area of the circle is 256/81 r². That is, pi is almost 3.16. They discovered this pi value about 4,000 years ago.


Figure 26 : Achmes' mathematical papyrus .
Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.
A thousand years later, the German mathematician Ludolf Zeilen worked with 2 62- sided polygons and received 35 decimal digits pi. This number, called Lyudolfov, was carved on his gravestone.



In 1706, the Englishman John Machin, who had long been a professor of astronomy, used the addition formula to prove that pi equals
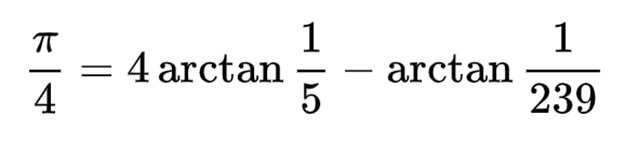
Not worried about where this formula came from, Macin began to use it constantly, and then wrote down the series shown below. This was the largest step at that time in the number of digits pi.

Figure 29 : Machin's formula for pi.
However, the first mention of pi appeared in 1706. Mathematics teacher William Jones wrote a book and first proposed pi for measuring circles. So pi first appeared in books!



Figure 30 : Juliabloggers
In 1873, William Shanks used the John Machin formula and received 707 decimal digits. These numbers are written in the room of the Paris Palace of Discoveries. However, later mathematicians found that only 527 digits were true.

Figure 31 : pi room
On the other hand, Buffon discovered a more interesting way of finding pi. His experiment was based on randomly scattering needles to evaluate pi. He drew several parallel lines on the board at a distance D and took needles of length L. Then he randomly started throwing needles on the board and wrote down the proportion of needles crossing the line.

Figure 32.0 : Science Friday
And after that, another mathematician named Lazzarini threw a needle 3408 times and received six decimal digits pi with a ratio of 355/113. However, if one needle did not cross the line, he would receive only 2 digits pi.

Figure 32.1 : Throwing 1000 needles to estimate the approximate pi
e: history of exponential growth
e is another famous irrational number. The fractional part e is also infinite, like pi. We use the number e to calculate power (exponential) growth. In other words, we use e when we see very fast growth or decrease.
One of the greatest, and perhaps the best mathematician, Leonard Euler discovered the number e in 1736 and first mentioned this special number in his book Mechanica .


Figure 33 : source
To understand exponential growth, we can use the story of a chess inventor. When he came up with this game, he showed it to the ruler of the North. The king liked the game and he promised that he would give the author any reward. Then the inventor asked for something very simple: 2 0 grains per first cell of a chessboard, 2 1 grains per second cell of a board, 2 2 grains per third, and so on. Each time, the amount of grain doubled. The king of the North thought that the request would be easy to fulfill, but he was mistaken, because it would be necessary to put 2 63 grainson the last cell, which is 9 223 372 036 854 775 808. This is exponential growth. It started at 1, doubled constantly, and after 64 steps it grew into a huge number!
If a chess inventor chose a linear equation, for example, 2n, he would get 2, 4, 6, 8, ... 128 ... Therefore, in the long run, exponential growth often far exceeds polynomial.
By the way, 9,223,372,036,854,775,808-1 is the maximum value of a 64-bit signed integer .


Figure 34 : source: Wikipedia
The number e was discovered by Euler. However, Jacob Bernoulli also worked with the number ewhen calculating compound interest to earn more money. If you invest $ 100 at 10% of the income, how will this amount grow? Firstly, it depends on how often the bank calculates interest. For example, if he calculates once, then we will receive $ 110 at the end of the year. If we change our minds and take interest every 6 months, then in this case we will receive more than 110 dollars. The fact is that the percentage received in the first 6 months will also receive its percentage. The total amount will be equal to 110.25 dollars. You can guess that we can get more money if we take money every quarter of the year. And if we make the time interval shorter, the final amounts will continue to grow. Such an infinite compound interest will make us rich! However, our total revenue tends to a limited value associated withe .
Bernoulli did not call the number 2.71828 by the name e . When Euler worked with 2.71828, he raised the exponential function e to the power of x . He outlined his discoveries in the book The Analysis of Infinite .
In 1798, Thomas Malthus used an exponential function in his essay on the nutritional deficiency of the future. He created a line graph showing food production and an exponential graph showing the world's population. Malthus concluded that in the long run, exponential growth will triumph, and the world is facing a serious food shortage. This phenomenon was called the "Malthusian catastrophe." Newton also used this model to show how a cup of tea cools.

Figure 35 : Newton-Richmann law

Рисунок 36: мальтузианская катастрофа
Мнимость числа: i, квадратный корень -1
For a long time, mathematicians had enough ordinary numbers to solve their problems. However, at some point for their further development they needed to discover something new and mysterious. For example, the Italian mathematician Cardano tried to divide the number 10 into 2 parts, the product of which would be equal to 40. To solve this problem, he wrote down the equation: x (10-x) = 40. When he solved this quadratic equation, he got two solutions: 5 plus √-15 and 5 minus √-15, which at that time did not make any sense. This result was meaningless, because by the definition of the square root he needed to find a number whose square would be negative. However, both positive and negative numbers squared have a positive value. Be that as it may, he found his unique number. However, the first mathematiciani was Euler.
Leibniz gave such a comment about the imaginary number √-1:
Complex numbers are a beautiful and wonderful refuge of the divine spirit, almost an amphibian of being with nothingness.
We can add, subtract, multiply and divide imaginary numbers. Addition, subtraction and multiplication are simple, and division is a little more complicated. The real and imaginary parts are folded separately. In the case of multiplication, i 2 will be equal to -1.
After Euler, mathematician Caspar Wessel introduced imaginary numbers geometrically and created a complex plane. Today we represent each complex number a + bi as a point with coordinates (a, b).
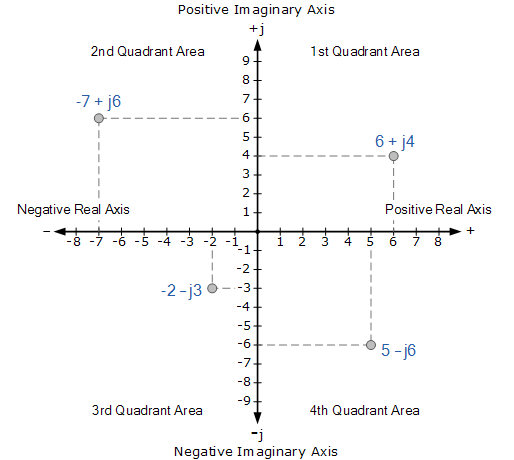

Figures 37 and 38 : complex numbers
In the Victorian era, many were suspicious of imaginary numbers. However, the Irish mathematician and astronomer William Rowan Hamilton ended these doubts by defining complex numbers as applied to quaternions .
The most beautiful equation: Euler's identity
Euler's identity connects an exponential function with sine and cosine functions, whose values range from minus one to one. To find a connection with trigonometric functions, we can represent them in the form of an infinite series, true for all values
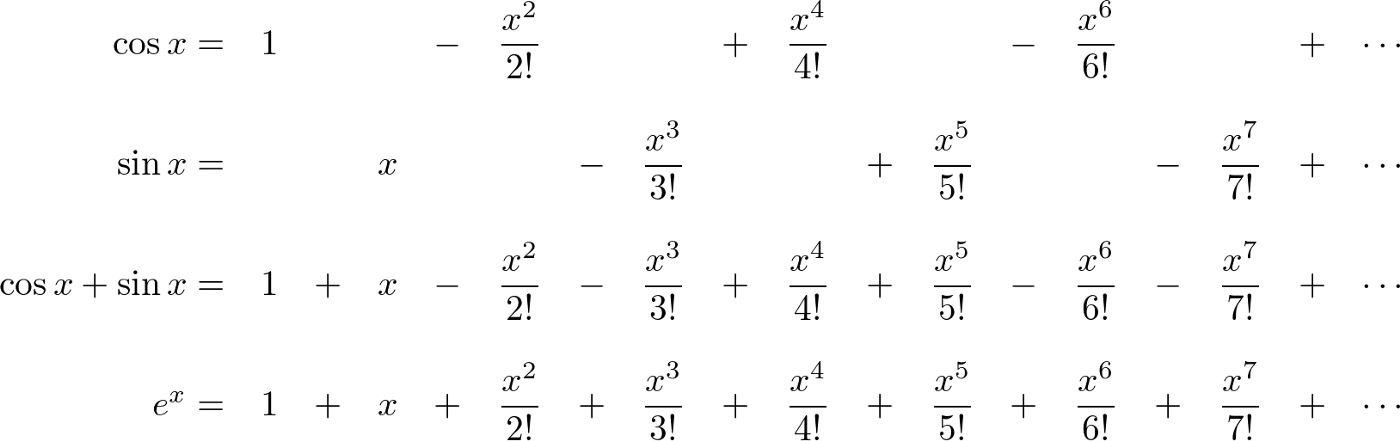
Figure 39 : Discovery of Euler Identity
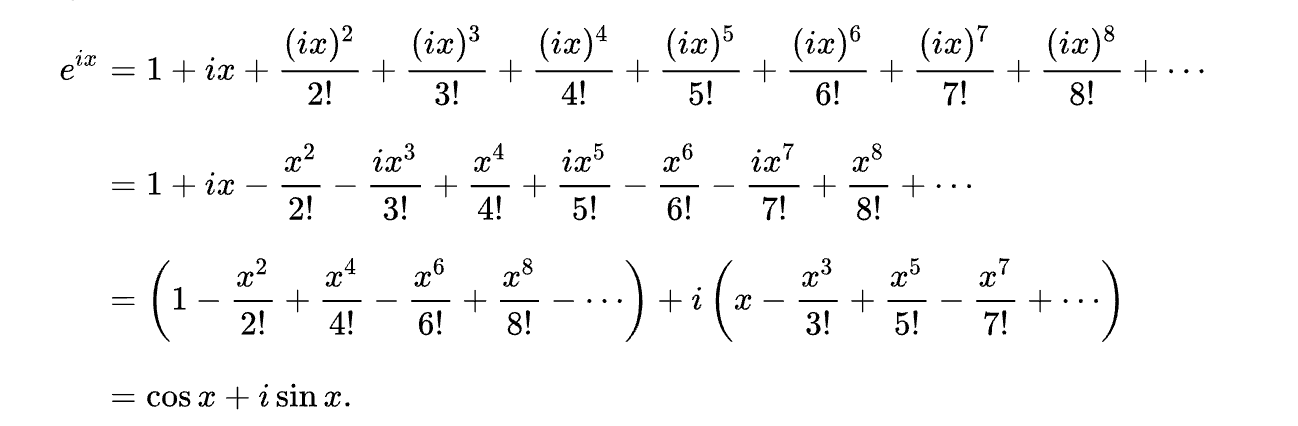
Figure 40 : Euler identity
Euler has never recorded this identity explicitly, and we do not know who first recorded it. Nevertheless, we associate it with the name of Euler in deference to this great pioneer of mathematics.
