Machine learning for everyone who studied math in eighth grade

Hello, Habr! I present to you the translation of the article "Machine Learning for Anyone Who Took Math in Eighth Grade" by Kyle Gallatin.

I usually notice that artificial intelligence can be explained in one of two ways: through the increasingly sensational prism of various media, or through dense scientific literature imbued with excessive language and area-specific terms.

Between these extremes, there is a less published area where, I think, literature should be a bit more active. Breaking news, like the stupid Sophia robot , takes hype around artificial intelligence and it might seem like something like a human mind, while in reality Sophia is no smarter than AOL Instant Messenger’s SmarterChild .

The scientific literature can be even worse, forcing even the most sophisticated researcher to close his eyes after a few paragraphs of meaningless pseudo-intellectual garbage. To properly evaluate AI , people must generally understand what it really is. And all you need to understand the basics of artificial intelligence is a little high school math.

I may be prone to oversimplification - and I will ask all my colleagues in mathematics, data science and engineering to tolerate my explanation - sometimes this is what artsy science needs.

Fundamentals of Artificial Intelligence and Machine Learning

Typical, classic artificial intelligence is all that mimics human intelligence. It can be anything from video game bots to complex platforms like Deepmind Alphago .

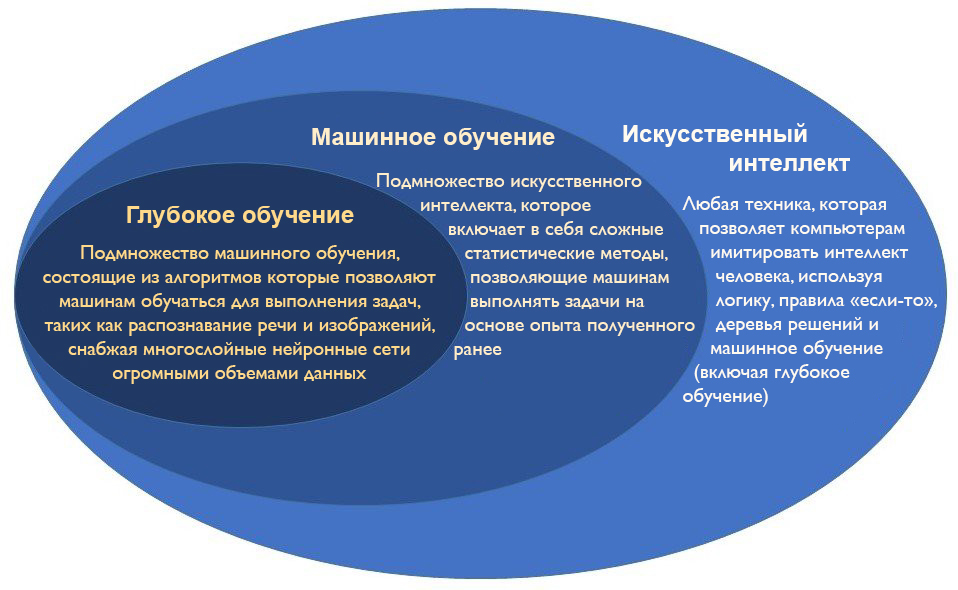
Ignore Deep Learning - in this context, it is the same as machine learning. Image: Geospatial World

Machine learning is a subset of artificial intelligence. This allows machines to “learn” from real data instead of acting on a set of predefined rules.

But what does learning mean? It may not be as futuristic as it seems.

My favorite explanation: machine learning is just $$on crack. If you watched something like Black Mirror , it’s quite easy to start imagining modern artificial intelligence as a conscious being — that which thinks, feels, and makes difficult decisions. This is even more common in the media, where the AI ​​is sequentially personified and then compared to Skynet from Terminator, or the film The Matrix.

In fact, this is not so at all. In its current state, artificial intelligence is just math. Sometimes it is complex mathematics, and sometimes it requires deep knowledge in the field of computer science, statistics and others. But in the end, modern AI at its core is just a mathematical function.

Do not worry if you are not friends with math functions because you don’t remember or use them. To get the gist, we need to remember just a few simple things: there is an input ($$) and there is a way out ($$), and the function is what happens between the input and the output - the connection between them.

We can make the computer look at the inbox ($$) and outgoing ($$) data and find out what binds them together.

An example of super-simplified artificial intelligence is a function expressed as $$. We already know$$ and $$(from the table below); we just need to find$$ and $$to understand what is the relationship between $$ and $$.

$$ (entrance)	$$ (exit)
1	2
2	3
3	4
4	5

Table: Kyle Gallatin

For this template to get $$ of $$we need to multiply $$ on 1 ($$) and add 1 ($$) So function will come out$$.

Excellent! We have determined that$$ and $$. We just took some data (from the table above) and created a function that described them. In essence, this is machine learning. Now, using the obtained function, we can make an assumption of what will be equal$$ for other input data $$.

The interesting part is how you teach the machine to find which function best describes the data, but when you are done with it, what you get is usually some form $$. As soon as we get this function, we can also build it on the chart:

Screenshot from Tecmath video

For a more detailed explanation of the functions, Math Is Fun has an intuitive and simple site (even if the name is a potential red flag for you, and the site looks like their web designer escaped sometime in the early 2000s).

People will not be able to count, cars will be able to

Obviously $$Is a very simple example. The only reason machine learning exists is because people cannot look at millions of in and out data points and come up with a complex function to describe the results. Instead, we can train the computer to do this for us.

In any case, there should be enough data to find the right function. If we only have one data point for$$ and $$, neither we nor the machine could predict only one exact function. In the original example, where$$ and $$function may be $$, $$, $$or many others. If we don’t have enough data, the function that the machine finds can lead to a lot of errors when we try to use it for more data.

In addition, real data is not always so perfect. In the example below, the machine has identified several functions that correspond to most of the data, but the line does not go through each point. Unlike the previous example with a table from a mathematical class, data collected from the real world are more unpredictable and can never be fully described.

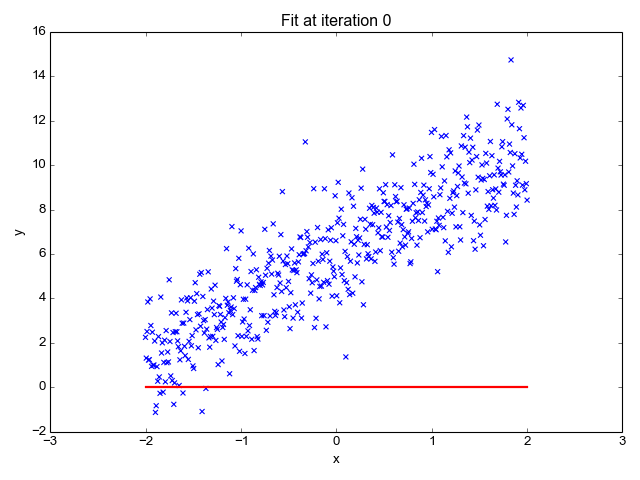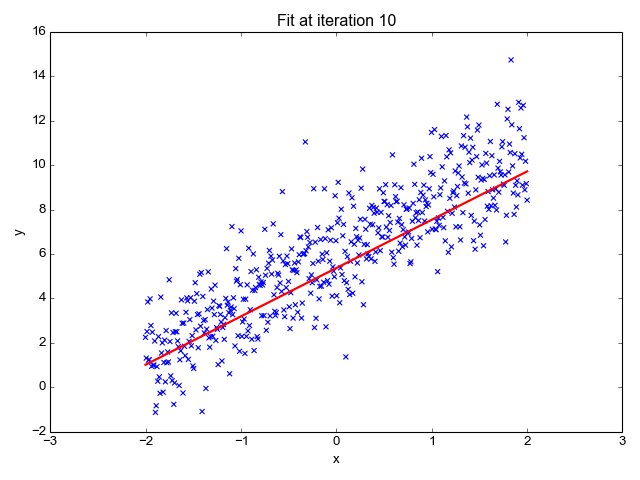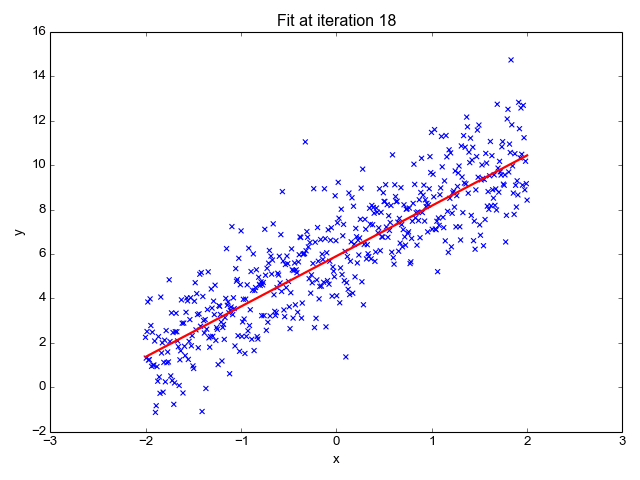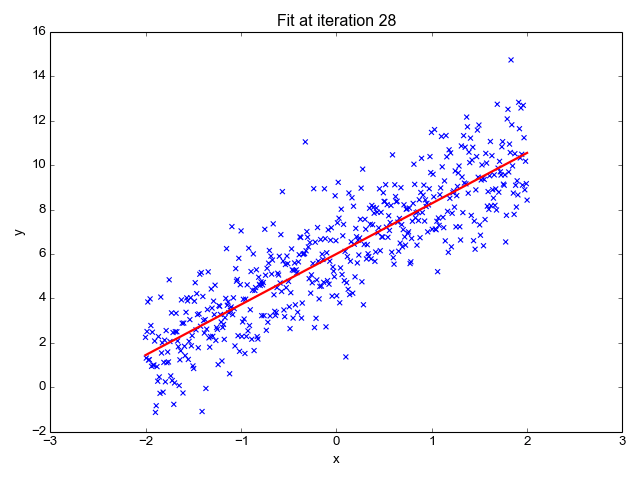
This basic example shows how a machine learns to best describe the data presented. Image: Towards Data Science

Finally, the last thing people cannot do is look at a bunch of variables. It's just using$$ and $$but what if there are more input variables? What if$$ affects $$, $$, ... $$. Very quickly, functions can become more complex (for people).

Real-world machine learning and artificial intelligence

Let's look at a real example. I work in the field of pharmaceuticals, so suppose we have a cancer-related data set that has two input variables that correspond to the size of the tumor - radius and perimeter, and output, with two possible values: whether the tumor is benign or metastatic (potentially dangerous for life). It may seem complicated, but we just need to apply a familiar concept$$:

• $$ is a diagnosis, and may be 0 (benign) or 1 (metastatic).
• $$ - radius.
• $$ - perimeter.
• Everyone has it $$ have your unknown $$; let's call them$$ and $$.
• $$ - unknown constant.

What does our linear equation look like now? Not much different from the example above:

Как я объяснил выше, мы выходим из области человеческих возможностей. Таким образом, вместо того, чтобы смотреть на данные и пытаться выяснить, на что мы должны умножить наши переменные, используем машины. Они сделают это за нас, и мы получим точную оценку диагноза. И это и есть машинное обучение!

Конечно, даже самые подробные, многофакторные данные не идеальны, поэтому и наша модель машинного обучения тоже такой не будет. Но нам и не нужно, чтобы они были правильны в 100% случаев. Мы просто нуждаемся в них, чтобы придумать наилучшую возможную функцию, которая подходит для большинства случаев.

This piece only scratches the surface of the incredible math and computer science that goes into machine learning. But even at complex levels, the concept is the same. No matter how impressive or strange machine learning and artificial intelligence may seem, it all comes from the functions that the machine learned to best describe the data.