June 6, 2019 at 15:30Distinguish characters from garbage: how to build robust neural network models in OCR tasks
Recently, in the ABBYY recognition group, we are increasingly using neural networks in various tasks. Very well they have proven themselves primarily for complex types of writing. In past posts, we talked about how we use neural networks to recognize Japanese, Chinese, and Korean scripts.
Post about recognition of Japanese and Chinese characters
Post about recognition of Korean characters
In both cases, we used neural networks to completely replace the classification method for a single symbol. All approaches included many different networks, and some of the tasks included the need to work adequately on images that are not symbols. The model in these situations should somehow signal that we are not a symbol. Today we’ll just talk about why this may be necessary in principle, and about approaches that can be used to achieve the desired effect.
What’s the problem? Why work on images that are not separate characters? It would seem that you can divide a fragment of a string into characters, classify them all and collect the result from this, as, for example, in the picture below.
Yes, specifically in this case, this really can be done. But, alas, the real world is much more complicated, and in practice, when recognizing, you have to deal with geometric distortions, blur, coffee stains and other difficulties.
As a result, you often have to work with such fragments:
I think it’s obvious to everyone what the problem is. According to such an image of a fragment, it is not so simple to unambiguously divide it into separate symbols in order to recognize them individually. We have to put forward a set of hypotheses about where the boundaries between the characters are, and where the characters themselves are. For this, we use the so-called linear division graph (GLD). In the picture above, this graph is shown at the bottom: the green segments are the arcs of the constructed GLD, that is, the hypotheses about where the individual symbols are located.
Thus, some of the images for which the individual character recognition module is launched are, in fact, not individual characters, but segmentation errors. And this same module should signal that in front of it, most likely, is not a symbol, returning low confidence for all recognition options. And if this does not happen, then in the end, the wrong option for segmenting this fragment by symbols can be chosen, which will greatly increase the number of linear division errors.
In addition to segmentation errors, the model must also be resistant to a priori garbage from the page. For example, here such images can also be sent to recognize a single character:
If you simply classify such images into separate characters, then the classification results will fall into the recognition results. Moreover, in fact, these images are simply artifacts of the binarization algorithm, nothing should correspond to them in the final result. So for them, too, you need to be able to return low confidence in the classification.
All similar images: segmentation errors, a priori garbage, etc. we will hereinafter be called negative examples. Images of real symbols will be called positive examples.
Now let's recall how a normal neural network works to recognize individual characters. Usually this is some kind of convolutional and fully connected layers, with the help of which the vector of probabilities of belonging to each particular class is formed from the input image.
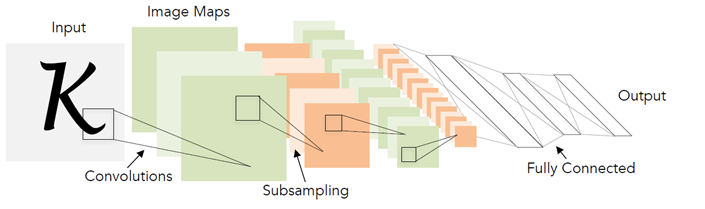
Moreover, the number of classes coincides with the size of the alphabet. During the training of the neural network, images of real symbols are served and taught to return a high probability for the correct symbol class.
And what will happen if a neural network is fed in with segmentation errors and a priori garbage? In fact, purely theoretically, anything can happen, because the network did not see such images at all in the learning process. For some images, it may be lucky, and the network will return a low probability for all classes. But in some cases, the network may begin to search among the garbage at the entrance for the familiar outlines of a certain symbol, for example, the symbol “A” and recognize it with a probability of 0.99.
In practice, when we worked, for example, on a neural network model for Japanese and Chinese writing, the use of crude probability from the output of the network led to the appearance of a huge number of segmentation errors. And, despite the fact that the symbolic model worked very well on the basis of images, it was not possible to integrate it into the full recognition algorithm.
Someone may ask: why exactly with neural networks does such a problem arise? Why did the attribute classifiers not work the same way, because they also studied on the basis of images, which means that there were no negative examples in the learning process?
The fundamental difference, in my opinion, is in how exactly signs are distinguished from symbol images. In the case of the usual classifier, a person himself prescribes how to extract them, guided by some knowledge of their device. In the case of a neural network, feature extraction is also a trained part of the model: they are configured so that it is possible to distinguish characters from different classes in the best way. And in practice, it turns out that the characteristics described by a person are more resistant to images that are not symbols: they are less likely to be the same as images of real symbols, which means that a lower confidence value can be returned to them.
Because the problem, according to our suspicions, was how the neural network selects signs, we decided to try to improve this particular part, that is, to learn how to highlight some “good” signs. In deep learning, there is a separate section devoted to this topic, and it is called “Representation Learning”. We decided to try various successful approaches in this area. Most of the solutions were proposed for the training of representations in face recognition problems.
The approach described in the article “ A Discriminative Feature Learning Approach for Deep Face Recognition ” seemed quite good . The main idea of the authors: to add an additional term to the loss function, which will reduce the Euclidean distance in the feature space between elements of the same class.
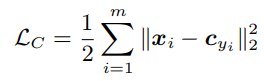
For various values of the weight of this term in the general loss function, one can obtain various images in the attribute spaces:
This figure shows the distribution of the elements of a test sample in a two-dimensional attribute space. The problem of classifying handwritten numbers is considered (sample MNIST).
One of the important properties that was stated by the authors: an increase in the generalizing ability of the obtained characteristics for people who were not in the training set. The faces of some people were still located nearby, and the faces of different people were far apart.
We decided to check whether a similar property for character selection is preserved. At the same time, they were guided by the following logic: if in the feature space all elements of the same class are grouped compactly near one point, then signs for negative examples will be less likely to be located near the same point. Therefore, as the main criterion for filtering, we used the Euclidean distance to the statistical center of a particular class.
To test the hypothesis, we performed the following experiment: we trained models for recognizing a small subset of Japanese characters from syllabic alphabets (the so-called kana). In addition to the training sample, we also examined 3 artificial bases of negative examples:
We wanted to compare the classic approach with the Cross Entropy loss function and the approach with Center Loss in their ability to filter negative examples. The filtering criteria for negative examples were different. In the case of Cross Entropy Loss, we used the network response from the last layer, and in the case of Center Loss, we used the Euclidean distance to the statistical center of the class in the attribute space. In both cases, we chose the threshold of the corresponding statistics, at which no more than 3% of positive examples from the test sample are eliminated and looked at the proportion of negative examples from each database that is eliminated at this threshold.
As you can see, the Center Loss approach really does a better job of filtering out negative examples. Moreover, in both cases, we did not have images of negative examples in the learning process. This is actually very good, because in the general case, getting a representative base of all the negative examples in the OCR problem is not an easy task.
We applied this approach to the problem of recognizing Japanese characters (at the second level of a two-level model), and the result pleased us: the number of linear division errors was reduced significantly. Although the mistakes remained, they could already be classified by specific types: be it pairs of numbers or hieroglyphics with a stuck punctuation symbol. For these errors, it was already possible to form some synthetic base of negative examples and use it in the learning process. About how this can be done, and will be discussed further.
If you have some collection of negative examples, then it is foolish not to use it in the learning process. But let's think about how this can be done.
First, consider the simplest scheme: we group all negative examples into a separate class and add another neuron to the output layer corresponding to this class. Now at the output we have a probability distribution for N + 1 class. And we teach this the usual Cross-Entropy Loss.
The criterion that the example is negative can be considered the value of the corresponding new network response. But sometimes real characters of not very high quality can be classified as negative examples. Is it possible to make the transition between positive and negative examples smoother?
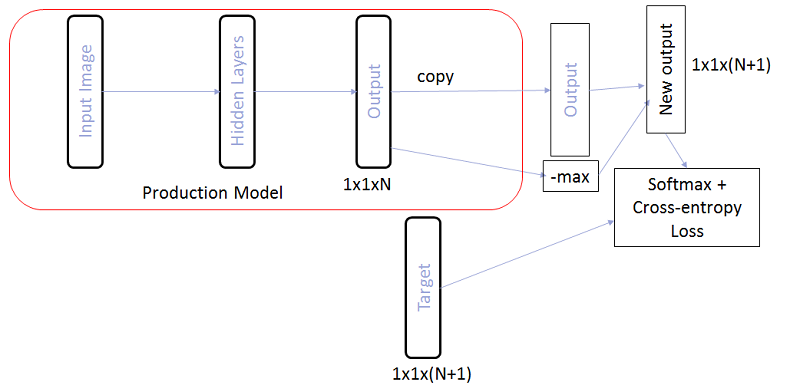
In fact, you can try not to increase the total number of outputs, but simply make the model, when learning, return low responses for all classes when applying negative examples to the input. To do this, we can not explicitly add the N + 1st output to the model , but simply add the value of –max from the responses for all other classes to the N + 1st element . Then, when applying negative examples to the input, the network will try to do as much as possible, which means that the maximum response will try to make as little as possible.
Exactly such a scheme we applied at the first level of a two-level model for the Japanese in combination with the Center Loss approach at the second level. Thus, some of the negative examples were filtered at the first level, and some at the second. In combination, we have already managed to obtain a solution that is ready to be embedded in the general recognition algorithm.
In general, one may also ask: how to use the base of negative examples in the approach with Center Loss? It turns out that somehow we need to put off the negative examples that are located close to the statistical centers of the classes in the attribute space. How to put this logic into the loss function?
Let be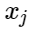
signs of negative examples, and let be the 
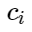centers of classes. Then we can consider the following addition for the loss function:
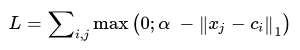
Here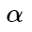
is a certain allowable gap between the center and negative examples, inside of which a penalty is imposed on negative examples.
The combination of Center Loss with the additive described above, we have successfully applied, for example, for some individual classifiers in the task of recognizing Korean characters.
In general, all the approaches to filtering the so-called “negative examples” described above can be applied in any classification problems when you have some implicitly highly unbalanced class relative to the rest without a good base of representatives, which nevertheless needs to be reckoned with somehow . OCR is just some particular task in which this problem is most acute.
Naturally, all these problems arise only when using neural networks as the main model for recognizing individual characters. When using End-to-End line recognition as a whole separate model, such a problem does not arise.
OCR New Technologies Group
Post about recognition of Japanese and Chinese characters Post about recognition of Korean charactersIn both cases, we used neural networks to completely replace the classification method for a single symbol. All approaches included many different networks, and some of the tasks included the need to work adequately on images that are not symbols. The model in these situations should somehow signal that we are not a symbol. Today we’ll just talk about why this may be necessary in principle, and about approaches that can be used to achieve the desired effect.
Motivation
What’s the problem? Why work on images that are not separate characters? It would seem that you can divide a fragment of a string into characters, classify them all and collect the result from this, as, for example, in the picture below.
Yes, specifically in this case, this really can be done. But, alas, the real world is much more complicated, and in practice, when recognizing, you have to deal with geometric distortions, blur, coffee stains and other difficulties.
As a result, you often have to work with such fragments:
I think it’s obvious to everyone what the problem is. According to such an image of a fragment, it is not so simple to unambiguously divide it into separate symbols in order to recognize them individually. We have to put forward a set of hypotheses about where the boundaries between the characters are, and where the characters themselves are. For this, we use the so-called linear division graph (GLD). In the picture above, this graph is shown at the bottom: the green segments are the arcs of the constructed GLD, that is, the hypotheses about where the individual symbols are located.
Thus, some of the images for which the individual character recognition module is launched are, in fact, not individual characters, but segmentation errors. And this same module should signal that in front of it, most likely, is not a symbol, returning low confidence for all recognition options. And if this does not happen, then in the end, the wrong option for segmenting this fragment by symbols can be chosen, which will greatly increase the number of linear division errors.
In addition to segmentation errors, the model must also be resistant to a priori garbage from the page. For example, here such images can also be sent to recognize a single character:
If you simply classify such images into separate characters, then the classification results will fall into the recognition results. Moreover, in fact, these images are simply artifacts of the binarization algorithm, nothing should correspond to them in the final result. So for them, too, you need to be able to return low confidence in the classification.
All similar images: segmentation errors, a priori garbage, etc. we will hereinafter be called negative examples. Images of real symbols will be called positive examples.
The problem of the neural network approach
Now let's recall how a normal neural network works to recognize individual characters. Usually this is some kind of convolutional and fully connected layers, with the help of which the vector of probabilities of belonging to each particular class is formed from the input image.
Moreover, the number of classes coincides with the size of the alphabet. During the training of the neural network, images of real symbols are served and taught to return a high probability for the correct symbol class.
And what will happen if a neural network is fed in with segmentation errors and a priori garbage? In fact, purely theoretically, anything can happen, because the network did not see such images at all in the learning process. For some images, it may be lucky, and the network will return a low probability for all classes. But in some cases, the network may begin to search among the garbage at the entrance for the familiar outlines of a certain symbol, for example, the symbol “A” and recognize it with a probability of 0.99.
In practice, when we worked, for example, on a neural network model for Japanese and Chinese writing, the use of crude probability from the output of the network led to the appearance of a huge number of segmentation errors. And, despite the fact that the symbolic model worked very well on the basis of images, it was not possible to integrate it into the full recognition algorithm.
Someone may ask: why exactly with neural networks does such a problem arise? Why did the attribute classifiers not work the same way, because they also studied on the basis of images, which means that there were no negative examples in the learning process?
The fundamental difference, in my opinion, is in how exactly signs are distinguished from symbol images. In the case of the usual classifier, a person himself prescribes how to extract them, guided by some knowledge of their device. In the case of a neural network, feature extraction is also a trained part of the model: they are configured so that it is possible to distinguish characters from different classes in the best way. And in practice, it turns out that the characteristics described by a person are more resistant to images that are not symbols: they are less likely to be the same as images of real symbols, which means that a lower confidence value can be returned to them.
Enhancing Model Stability with Center Loss
Because the problem, according to our suspicions, was how the neural network selects signs, we decided to try to improve this particular part, that is, to learn how to highlight some “good” signs. In deep learning, there is a separate section devoted to this topic, and it is called “Representation Learning”. We decided to try various successful approaches in this area. Most of the solutions were proposed for the training of representations in face recognition problems.
The approach described in the article “ A Discriminative Feature Learning Approach for Deep Face Recognition ” seemed quite good . The main idea of the authors: to add an additional term to the loss function, which will reduce the Euclidean distance in the feature space between elements of the same class.
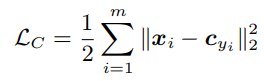
For various values of the weight of this term in the general loss function, one can obtain various images in the attribute spaces:
This figure shows the distribution of the elements of a test sample in a two-dimensional attribute space. The problem of classifying handwritten numbers is considered (sample MNIST).
One of the important properties that was stated by the authors: an increase in the generalizing ability of the obtained characteristics for people who were not in the training set. The faces of some people were still located nearby, and the faces of different people were far apart.
We decided to check whether a similar property for character selection is preserved. At the same time, they were guided by the following logic: if in the feature space all elements of the same class are grouped compactly near one point, then signs for negative examples will be less likely to be located near the same point. Therefore, as the main criterion for filtering, we used the Euclidean distance to the statistical center of a particular class.
To test the hypothesis, we performed the following experiment: we trained models for recognizing a small subset of Japanese characters from syllabic alphabets (the so-called kana). In addition to the training sample, we also examined 3 artificial bases of negative examples:
- Pairs - a set of pairs of European characters
- Cuts - fragments of Japanese lines cut in gaps, not characters
- Not kana - other characters from the Japanese alphabet that are not related to the considered subset
We wanted to compare the classic approach with the Cross Entropy loss function and the approach with Center Loss in their ability to filter negative examples. The filtering criteria for negative examples were different. In the case of Cross Entropy Loss, we used the network response from the last layer, and in the case of Center Loss, we used the Euclidean distance to the statistical center of the class in the attribute space. In both cases, we chose the threshold of the corresponding statistics, at which no more than 3% of positive examples from the test sample are eliminated and looked at the proportion of negative examples from each database that is eliminated at this threshold.
As you can see, the Center Loss approach really does a better job of filtering out negative examples. Moreover, in both cases, we did not have images of negative examples in the learning process. This is actually very good, because in the general case, getting a representative base of all the negative examples in the OCR problem is not an easy task.
We applied this approach to the problem of recognizing Japanese characters (at the second level of a two-level model), and the result pleased us: the number of linear division errors was reduced significantly. Although the mistakes remained, they could already be classified by specific types: be it pairs of numbers or hieroglyphics with a stuck punctuation symbol. For these errors, it was already possible to form some synthetic base of negative examples and use it in the learning process. About how this can be done, and will be discussed further.
Using the base of negative examples in training
If you have some collection of negative examples, then it is foolish not to use it in the learning process. But let's think about how this can be done.
First, consider the simplest scheme: we group all negative examples into a separate class and add another neuron to the output layer corresponding to this class. Now at the output we have a probability distribution for N + 1 class. And we teach this the usual Cross-Entropy Loss.
The criterion that the example is negative can be considered the value of the corresponding new network response. But sometimes real characters of not very high quality can be classified as negative examples. Is it possible to make the transition between positive and negative examples smoother?
In fact, you can try not to increase the total number of outputs, but simply make the model, when learning, return low responses for all classes when applying negative examples to the input. To do this, we can not explicitly add the N + 1st output to the model , but simply add the value of –max from the responses for all other classes to the N + 1st element . Then, when applying negative examples to the input, the network will try to do as much as possible, which means that the maximum response will try to make as little as possible.
Exactly such a scheme we applied at the first level of a two-level model for the Japanese in combination with the Center Loss approach at the second level. Thus, some of the negative examples were filtered at the first level, and some at the second. In combination, we have already managed to obtain a solution that is ready to be embedded in the general recognition algorithm.
In general, one may also ask: how to use the base of negative examples in the approach with Center Loss? It turns out that somehow we need to put off the negative examples that are located close to the statistical centers of the classes in the attribute space. How to put this logic into the loss function?
Let be
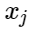signs of negative examples, and let be the 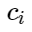centers of classes. Then we can consider the following addition for the loss function: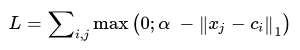Here
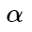is a certain allowable gap between the center and negative examples, inside of which a penalty is imposed on negative examples. The combination of Center Loss with the additive described above, we have successfully applied, for example, for some individual classifiers in the task of recognizing Korean characters.
conclusions
In general, all the approaches to filtering the so-called “negative examples” described above can be applied in any classification problems when you have some implicitly highly unbalanced class relative to the rest without a good base of representatives, which nevertheless needs to be reckoned with somehow . OCR is just some particular task in which this problem is most acute.
Naturally, all these problems arise only when using neural networks as the main model for recognizing individual characters. When using End-to-End line recognition as a whole separate model, such a problem does not arise.
OCR New Technologies Group