New Frontiers in Physics
Hello dear reader! I present to you the translation from English of the article “Physics, The Next Frontier” by Chris Hecker.
I, a novice Java developer, was faced with the fact that the materials for creating a physical in-game engine are presented only in English, therefore this article was translated. There will be three more articles in the series, I will post them as soon as possible. Enjoy reading!
There is no doubt that every year the in-game graphics are becoming more realistic. Already today, everyone creates (or at least shows screenshots) 3D worlds with texture maps, and when enough hardworking people get together to work on one project, each developer can draw billions of polygons of realistic textures and shadows per second. In technical terms, what remains to be done to create a game at a high level? Will every developer with a copy of the book “Learn to Use 3D Hardware in 21 Days” be able to create a truly impressive game?
Not at all. Upscale developers will continue to raise the bar in many different technologies (such as GUI complexity, artificial intelligence, and networking). Of course, all this is very important, we can’t even seriously discuss any of them without specifying details. Nevertheless, there is one technology applicable to everything, which, in my opinion, will become a decisive factor in the near future: physics.
Consider the following example: do you remember these huge spinning gears in one of the early levels of Duke Nukem 3D?

Figure 1. Screenshot from the game "Duke Nukem 3D"
Just imagine that their rotation would be described not by cyclic animation, but by a real physical engine. Suddenly, the gears become something more than a game decoration, just as one of them deviates from the given angle, and rolls down the corridor behind you, as in the Indiana Jones films. Or imagine that after shooting a gear from a rocket launcher, it will roll down the corridor and crush your friend, who has crept up behind to kill you! Physical engines make such situations real.
Physical simulation is what makes the game world whole: thanks to it, “here” is located here, if you understand what I mean. Any magic in the graphics in the world will not allow the player to plunge into the game process if he will interpenetrate into another player, or into the walls of the level, or if the mass and moment of mass are not felt. The animators at Disney found this feeling of the masses to be what separates good animation from bad animation. According to the epic book Disney Animation: The Illusion of Life by Frank Thomas and Ollie Johnston, Disney animators, even just hanging a poster in the studio, should always ask themselves: “Is there a lot of weight, depth and balance in their drawing?” ? "
But today almost every game has a physics engine, right? Undoubtedly, this is what keeps your car from falling over the edge of the game world, thanks to it your characters do not fly into space when they jump, and this throws your boat to the side when a rocket explodes nearby. However, most physical engines in modern games are pretty weak. They cope only with the task of keeping the car from falling over the edge of the world, but their capabilities are not enough to take the game to a new level - where the wreckage of a wrecked car can explode right on the track, causing a roll of walls and other cars.
Other physical effects that are often ignored include: from simple twisting effects as a result of a tangent strike, to the characters in the game themselves keeping their balance and moving, unlike statically animated ones. I believe that many developers ignore these possibilities because they do not understand the mathematics that describe physics, or were too busy creating texture maps to learn it. The onslaught of hardware for working with 3D will take care of the latter, and I am starting a new series of articles. The first article will take care of the formalities. By the end of our cycle, you yourself can create a physical engine that will make players feel completely immersed in the gameplay, thanks to incredible realism, or an entertaining but persistent surrealism.
Warning! Physics = mathematics, in order to complete an interesting project, you will have to use both. Before this scares you off, let me note that the mathematics that describe physics is not only elegant and beautiful, it also has an applied character. That is, it is not abstract mathematics for mathematics. Each equation we use has a real physical meaning. We create equations from a physical model, and in return the equations tell us how the model behaves in time.
Physics is a wide scientific field. But we are really interested in its small section called “dynamics”, or more precisely, “dynamics of solids”. Dynamics can be defined in terms of a related section - kinematics (the doctrine of the movement in time). Kinematics does not focus on what causes the movement or how the bodies ended up where they are, it simply describes the movement. Dynamics, on the contrary, describes the forces and masses that contribute to the values from kinematics to change over time. How far the baseball ball will fly if the flight time is 10 seconds and its initial speed is 50 kilometers / hour, and the trajectory is a straight line - this is a kinematic problem; how far the baseball ball will fly in the gravitational field of the earth, if I hit it with a bat - this is a dynamic problem.
The part of the dynamics that describes solids relates to the constraints that we add for simulated objects. The shape of a solid body does not change during the simulation - the body is more likely wooden or metal than jelly-like. We can create articulated figures, for example, of a person, by constructing each part of the figure from a solid body and creating ligaments between them, but we won’t count on bones bending under the stress or similar effects. This will allow us to simplify our equations without losing the quality of the interesting dynamic behavior of bodies.
Even though we will consider such a small part of the dynamics, the dynamics of a rigid body will require a series of articles to explain the essence. We begin our journey by studying the basics of computer programming to describe the motion of a plane rigid body under the action of forces. I persistently repeat “computer programming”, because in addition to the equations that we write for kinematics and dynamics, we will also learn how to solve these equations using floating-point calculations, which is vital for every programmer to know. I say “flat solid” because we will only deal with the two-dimensional world throughout the next article and beyond. The principles - and in fact more than just equations - can also be transferred to the three-dimensional world, but definitely everything is much simpler in the two-dimensional world, so we will study there, until we feel confident to exit into three-dimensional space. In future articles, we will learn to describe the effect of rotation, the processing of contacts of bodies, and, of course, how to do all this in a three-dimensional world. Well, enough words! Let's start!
This may come as a surprise to you, but you really cannot move an object by simply pushing it. I know, you think I'm wrong in proving the opposite to me by throwing this magazine in the trash for writing such nonsense, but it's true! Only putting pressure on a magazine will never directly affect its position in space. In fact, pressure does not even directly affect its speed. What pressure actually affects is the acceleration of the journal, and in fact it is one of the most important conclusions in the history of science.
In order to use this fact in order to do something interesting, we first need to talk about the relationship of the position of the body with speed and acceleration. In fact, all these values are very closely related (as you probably know): speed is an indicator of changes in the coordinates of the body over time, and acceleration is an indicator of changes in speed. The primary tool for studying changes in these quantities over time is differential calculus. If you understand this, then we move on. I suppose you are good at math. We will use only simple scalar and vector calculations (derivatives and integrals), but it will not be superfluous if you are familiar with mathematics as a whole. For reference: my favorite book on computing is Calculus with Analytic Geometry by Thomas and Finney.
Coordinate, speed and acceleration are kinematics that will be discussed in this article. The location of a solid in a two-dimensional world is, obviously, a pair of coordinates X and Y, which denote the coordinates of the space of some given point of the body. The derivative for the coordinate vector is the velocity vector, and it shows us in which direction the point is moving (and the body, if we ignore the rotation, which is happening now) and how fast it is moving. The vector calculus is just the scalar calculus of each element of the vector, so the derivative of the X coordinate is the body velocity with respect to X, and so on. We introduce the following notation. Let the coordinate of the body be the vector r, and the velocity be the vector v or the vector r with a prime. We get the equation:
Equation 1
If we differentiate the velocity vector with respect to time, this will show how the coordinate vector changes with time. Acceleration is determined by analogy. This is the first derivative of speed or the second derivative of the coordinate vector:
Equation 2
The integral of acceleration gives us speed, and integrating acceleration twice, we get the coordinate.
These relationships in kinematics show that we can find the acceleration of an object, we can integrate it over time to get the speed and coordinate. As we will see later, we will turn to integration many times in our simulation code and will calculate a new position for our solid for each frame. Hooray animation!
Here is a simple example for a one-dimensional world that we can analytically integrate. Let's agree that we want to find the coordinate change from the end of the last frame to the time of the current frame to draw the current position. Next, we say that the acceleration of our solid was equal to 5 arbitrary units / second ^ 2. We will use the time elapsed from the end of the last frame as a variable t (in the integration element dt).
Equation 3
The above equations show that speed is a function of time elapsed from the last frame. We found the integration constant, C, which is equal to the initial velocity at the beginning of the integration period (at t = 0).
Equation 4
Now we integrate our velocity equation to find the coordinate (again, do not forget about the integration constant):
Equation 5
Based on Equation 5, we can find the current position only by a given acceleration if we know the initial coordinate and speed (which we will take from the last frame) and the elapsed time. The input variable is time, and the value of the function is the current position. We will also indicate the time in Equation 4 in order to calculate the final speed so that we can use this as the initial condition for the next frame.
Now we have the realization that we need to set the acceleration correctly to integrate the kinematics equations in order to get the animation. The output of the speakers on stage. Remember, as I said, by pressing on something, you directly affect only the acceleration of the body? Well, “exerting pressure” is just a euphemism for the phrase “apply force” - one of the two key variables in dynamics - and now we can turn to Newton to find out how forces affect acceleration. Newton’s second law connects the force F with the derivative of the mass — the second magnitude of the dynamics — times velocity. The product of mass and speed is called the "momentum of the body", denoted by p:
Equation 6
Mass is a constant for the speeds we are working with now, this follows from the derivative in Equation 6, and we got the well-known equation F = ma (although I’m sure that Newton initially determined the force through the derivative of the momentum).
If we were dealing only with material points, Equation 6 is what we need in dynamics. For a given force of a given material point, acceleration is found by dividing the force by mass. This gives us acceleration, which will help solve the equation of motion from the example above. Nevertheless, we are dealing with solids with mass distributed over a certain area (volume, when it comes to the three-dimensional world), so we still need to work.
First, consider a solid as a set of point masses. We will define the total momentum, pT, for a solid, as the sum of the momenta of all the points that make up the body (I use the upper indexing, because I want to show more clearly what quantitative values belong to these points):
Equation 7
We can greatly simplify the analysis of the dynamics of a rigid body by introducing the concept of the center of mass (CM). A vector directed to the center of mass is a linear sum of vectors directed from all points of mass of a solid body divided by the mass of the whole body, M:
Equation 8
Using the definition of the center of mass, we can simplify Equation 7 by multiplying both sides of Equation 8 by M, differentiating them, and then substituting the result in Equation 7:
Equation 9
The right side of Equation 9 is the total momentum as defined in Equation 7. Now let's look at the left side of the equation: this is the speed at the center of mass multiplied by the mass of the whole body. Move the right side to the left and get:
Equation 10
From Equation 10 it follows that the linear momentum is equal to the total mass times the velocity directed from the center of mass, so there is no need to sum in Equation 7 in order to find the momentum if we know the mass of the body and the direction of the velocity vector of the center of mass. Further, all the final results of the calculations are finding the integrals for the whole body, but the center of mass exists and greatly simplifies the determination of the total momentum from Equation 10, so we can not worry - to find the linear momentum we can consider the body as a material point with given speed and mass.
By analogy, the total force is a derivative of the total momentum, so the concept of the center of mass can be used to simplify the equation of force:
Equation 11
In short, it follows from Equation 11 that we can consider all the forces interacting with a solid, as if their sum vector had an effect on the point of the center of mass, which contains the mass of the whole body. We divide the force (read gravity) by M in order to find the acceleration of the center of mass, and then integrate the acceleration in time in order to obtain the speed and coordinate of the body. Because we ignore the effects of rotation until the next article; we already have all the equations that we need to describe the dynamics of a rigid body. Note that Equation 11 does not contain information about where the forces applied to the body are directed. This will pop up when we deal with the linear momentum and the center of mass, and we just apply forces to the CM to find the acceleration of the center of mass.
At this stage, we can consider another example of analytical integration, using Equation 11 to find the acceleration of the center of mass instead of an arbitrarily chosen value = 5. Nevertheless, we face a serious problem, since analytical integration usually does not have an applied value, because it is too complicated, so we will focus on the so-called numerical integration of ordinary differential equations (ODEs). Wow, now that sounds like real math! Once you learn this, it will be time to raise the bar. Fortunately, the numerical integration of ODEs is not as difficult as it might seem at first glance! In order to understand what this means, we move from words to deeds!
So, a differential equation is an equation that contains derivatives of dependent quantities in addition to the function itself, independent variables and parameters. This is verbose, but here is an example for a time-varying force in a one-dimensional world: F = 2t, F is a dependent quantity, and t is independent. The value of F is determined only by F. Let the equation of force depend only on the speed of our body. The force of air resistance increases with increasing speed of the aircraft. Let us return to the example in the one-dimensional world, what if F = -v means that the friction force slows down our body in proportion to speed? We have a problem, because we solve the equation as follows: F = ma = -v and, dividing by m, we get (remember that acceleration is a derivative of speed):
Equation 12
This differential equation, (the velocity equation contains the velocity derivative in Equation 12) is called the ordinary differential equation, because it contains only ordinary derivatives of dependent quantities (as opposed to partial derivatives, which make up partial differential equations [PDEs], about which we are not will talk).
Now let's move on to the next part of our phrase: integration. How did we previously integrate dv / dt to find v in the conditions of this equation?
This will seem unbelievable, but almost every equation in physics is differential, so ODEs have been well studied. Differential equations can so often be found in physics, because often the rate of change of a quantitative quantity depends on the quantity itself. For example, we have already noted that braking (the magnitude of a change in speed), including the speed of air resistance, depends on speed. Other examples from physics: cooling (the rate of heat loss depends on the current temperature) and radioactive decay (decay rate depends on how much radioactive material is present).
The final word in our phrase - numerical - is our salvation. I say this because the theory of analytic integration of differential equations, even the simplest ones, is huge and rather confusing. Although, ironically, the integration of ODEs using computer numerical methods is actually relatively easy to understand. Next, I will describe a simple numerical integrator based on the Euler method, and will refine it in the next article.
Almost all numerical integrators, but no other one as explicit as the Euler method, are simply based on the old definition of computing through the first derivative of the slant: dy / dx determines the slope of y depending on x. For example, if we have the linear equation y = 5x, then dy / dx = 5 means that the slope is a constant equal to 5 for any x, and, as you can assume, this is a straight line. A slightly more difficult example is the parabola y = x2. In this case, dy / dx = 2x, and this is a function to determine the new slant for each x coordinate. I depicted y = x2 in Figure 2:
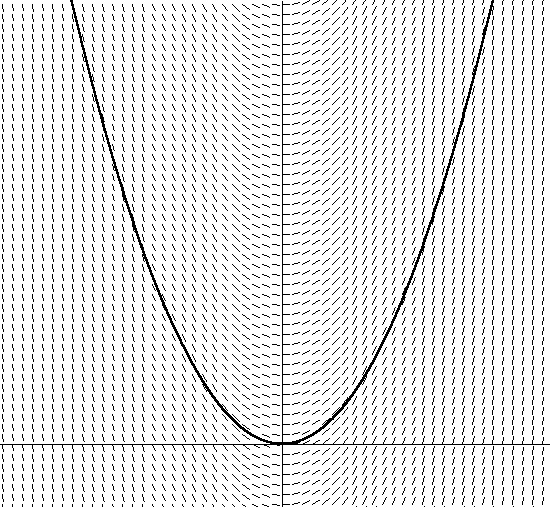
Figure 2. y = x2
In addition to this, I also hatched the direction of the vector oblique by solving the equation dy / dx = 2x + C for all x. Pay attention to the fact that the angle of the inclined vector is equal to the tangent of the tangent angle at this point. Note also that there are many different parabolas that satisfy the angle of the set of tangents, differing only in a shift along the y axis. Each of these parabolas is obtained by using different integration constants, which are contained in the equation dy / dx = 2x + C. The parabola that I pictured has an integration constant of 0. If I choose another constant, for example, 1, I get the equation y = 2x + 1. This means that there is a similar parabola with a shift of 1 unit up the y axis.
Now think about the fact that if you do not know the field of vectors in Figure 2 defined by a parabola, then just sit in a puddle. So, if you want to solve the tangent equation, you just need to follow the direction of the vector at each point, changing direction in accordance with the change in direction of the vector field. You will be surprised that after some time, you will see that you are moving along a parabolic trajectory (or along a section of the parabola), depending on where you started. Without realizing it, you integrated the equation of the vector field. You found a specific parabola (depending on where you started, or on the initial conditions), using only the derivative equation (calculating dy / dx as you move in the vector field).
Doing the same for a real differential equation is also simple. For a differential equation of the type dy / dx = f (x, y), finding the derivative dy / dx as tangent to f (x, y) describes the angle of inclination of the tangent for each coordinate on the x, y graph. If you are plotting a vector field given by dy / dx = f (x, y), you can follow this by analogy with a parabola by finding the derivative at each point and following in that direction. Figure 2 shows the vector field for Equation 12, our equation of air resistance, with velocity along the vertical axis and time along the horizontal (I arbitrarily chose m = 1 for this graph).
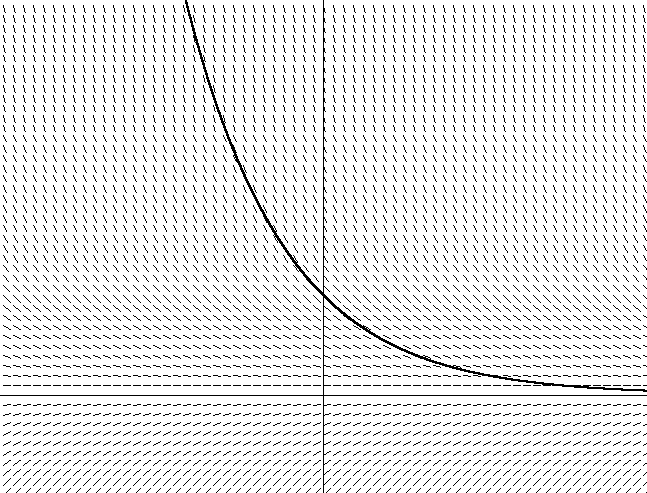
Figure 3. dv / dt = -v / m
It also shows one of the many possible curves. You may notice that if you choose the initial position in the graph (which depends on the initial speed in the equation), over time, the speed will tend to zero, because the friction force slows down the body. You can also see how the decrease in speed depends on the current value of speed - the faster you move, the faster it decreases. This becomes apparent when the same follows from Equation 12.
Numerical integration is similar to what we did on the chart. The Euler algorithm for numerical integration simply follows the vector field in accordance with the initial position by finding the derivative of the equation (-v / m for our example with the friction force) to determine the slope at the current point, and then simply moves forward step by step in time, depending on unchanged value of h, along the slope. Then a new position is calculated to determine the new slope after a certain time interval:
Or more precisely for our equation of air resistance:
Obviously, the Euler method gives a small error with each time step, since the real velocity vector (and therefore the solution curve) bends with a deviation at each point, and the Euler algorithm deviates slightly from the angle of inclination. But if the time step, h are rather small quantities, the error tends to zero. We will discuss this in more detail in the future.
This is all you need to know about numerical integration using the Euler method. You may ask how we are going to integrate the speed to get the coordinate. We simply use the Euler method again to integrate dr / dt = v, just as we integrated dv / dt = a, by analogy. We get two connected differential equations (one more of our victory):
This gives us an alternative algorithm for calculating the coordinate after the action of any arbitrarily applied force on our object (which may depend on the speed, as we saw, or time, or even the position of our body and other bodies, or all at once!). For the Euler method, it does not matter what the applied force looks like, because you can calculate it at any moment in time. Euler is interested in the magnitude of the effect of force on the mass, as inclined, and that’s it.
I ran out of space, so I have no way to provide links. Next time I will advise various wonderful books, and we will figure out how to calculate the rotation of solids.
And although his body is not as solid as we would like, Chris Hecker has a dynamic personality. If you apply force, he will answer e-mail checker@bix.com.
Translator's notes: a pun is presented here, the topic of the article and its content are played out.
PS The author of the translation expresses special thanks to the users of berez and MarazmDed for their editing of the translation. Thanks!
I, a novice Java developer, was faced with the fact that the materials for creating a physical in-game engine are presented only in English, therefore this article was translated. There will be three more articles in the series, I will post them as soon as possible. Enjoy reading!
New frontiers in physics
There is no doubt that every year the in-game graphics are becoming more realistic. Already today, everyone creates (or at least shows screenshots) 3D worlds with texture maps, and when enough hardworking people get together to work on one project, each developer can draw billions of polygons of realistic textures and shadows per second. In technical terms, what remains to be done to create a game at a high level? Will every developer with a copy of the book “Learn to Use 3D Hardware in 21 Days” be able to create a truly impressive game?
Not at all. Upscale developers will continue to raise the bar in many different technologies (such as GUI complexity, artificial intelligence, and networking). Of course, all this is very important, we can’t even seriously discuss any of them without specifying details. Nevertheless, there is one technology applicable to everything, which, in my opinion, will become a decisive factor in the near future: physics.
Consider the following example: do you remember these huge spinning gears in one of the early levels of Duke Nukem 3D?

Figure 1. Screenshot from the game "Duke Nukem 3D"
Just imagine that their rotation would be described not by cyclic animation, but by a real physical engine. Suddenly, the gears become something more than a game decoration, just as one of them deviates from the given angle, and rolls down the corridor behind you, as in the Indiana Jones films. Or imagine that after shooting a gear from a rocket launcher, it will roll down the corridor and crush your friend, who has crept up behind to kill you! Physical engines make such situations real.
Physical simulation is what makes the game world whole: thanks to it, “here” is located here, if you understand what I mean. Any magic in the graphics in the world will not allow the player to plunge into the game process if he will interpenetrate into another player, or into the walls of the level, or if the mass and moment of mass are not felt. The animators at Disney found this feeling of the masses to be what separates good animation from bad animation. According to the epic book Disney Animation: The Illusion of Life by Frank Thomas and Ollie Johnston, Disney animators, even just hanging a poster in the studio, should always ask themselves: “Is there a lot of weight, depth and balance in their drawing?” ? "
But today almost every game has a physics engine, right? Undoubtedly, this is what keeps your car from falling over the edge of the game world, thanks to it your characters do not fly into space when they jump, and this throws your boat to the side when a rocket explodes nearby. However, most physical engines in modern games are pretty weak. They cope only with the task of keeping the car from falling over the edge of the world, but their capabilities are not enough to take the game to a new level - where the wreckage of a wrecked car can explode right on the track, causing a roll of walls and other cars.
Other physical effects that are often ignored include: from simple twisting effects as a result of a tangent strike, to the characters in the game themselves keeping their balance and moving, unlike statically animated ones. I believe that many developers ignore these possibilities because they do not understand the mathematics that describe physics, or were too busy creating texture maps to learn it. The onslaught of hardware for working with 3D will take care of the latter, and I am starting a new series of articles. The first article will take care of the formalities. By the end of our cycle, you yourself can create a physical engine that will make players feel completely immersed in the gameplay, thanks to incredible realism, or an entertaining but persistent surrealism.
Warning! Physics = mathematics, in order to complete an interesting project, you will have to use both. Before this scares you off, let me note that the mathematics that describe physics is not only elegant and beautiful, it also has an applied character. That is, it is not abstract mathematics for mathematics. Each equation we use has a real physical meaning. We create equations from a physical model, and in return the equations tell us how the model behaves in time.
Grand enterprise
Physics is a wide scientific field. But we are really interested in its small section called “dynamics”, or more precisely, “dynamics of solids”. Dynamics can be defined in terms of a related section - kinematics (the doctrine of the movement in time). Kinematics does not focus on what causes the movement or how the bodies ended up where they are, it simply describes the movement. Dynamics, on the contrary, describes the forces and masses that contribute to the values from kinematics to change over time. How far the baseball ball will fly if the flight time is 10 seconds and its initial speed is 50 kilometers / hour, and the trajectory is a straight line - this is a kinematic problem; how far the baseball ball will fly in the gravitational field of the earth, if I hit it with a bat - this is a dynamic problem.
The part of the dynamics that describes solids relates to the constraints that we add for simulated objects. The shape of a solid body does not change during the simulation - the body is more likely wooden or metal than jelly-like. We can create articulated figures, for example, of a person, by constructing each part of the figure from a solid body and creating ligaments between them, but we won’t count on bones bending under the stress or similar effects. This will allow us to simplify our equations without losing the quality of the interesting dynamic behavior of bodies.
Even though we will consider such a small part of the dynamics, the dynamics of a rigid body will require a series of articles to explain the essence. We begin our journey by studying the basics of computer programming to describe the motion of a plane rigid body under the action of forces. I persistently repeat “computer programming”, because in addition to the equations that we write for kinematics and dynamics, we will also learn how to solve these equations using floating-point calculations, which is vital for every programmer to know. I say “flat solid” because we will only deal with the two-dimensional world throughout the next article and beyond. The principles - and in fact more than just equations - can also be transferred to the three-dimensional world, but definitely everything is much simpler in the two-dimensional world, so we will study there, until we feel confident to exit into three-dimensional space. In future articles, we will learn to describe the effect of rotation, the processing of contacts of bodies, and, of course, how to do all this in a three-dimensional world. Well, enough words! Let's start!
Work with a derivative
This may come as a surprise to you, but you really cannot move an object by simply pushing it. I know, you think I'm wrong in proving the opposite to me by throwing this magazine in the trash for writing such nonsense, but it's true! Only putting pressure on a magazine will never directly affect its position in space. In fact, pressure does not even directly affect its speed. What pressure actually affects is the acceleration of the journal, and in fact it is one of the most important conclusions in the history of science.
In order to use this fact in order to do something interesting, we first need to talk about the relationship of the position of the body with speed and acceleration. In fact, all these values are very closely related (as you probably know): speed is an indicator of changes in the coordinates of the body over time, and acceleration is an indicator of changes in speed. The primary tool for studying changes in these quantities over time is differential calculus. If you understand this, then we move on. I suppose you are good at math. We will use only simple scalar and vector calculations (derivatives and integrals), but it will not be superfluous if you are familiar with mathematics as a whole. For reference: my favorite book on computing is Calculus with Analytic Geometry by Thomas and Finney.
Coordinate, speed and acceleration are kinematics that will be discussed in this article. The location of a solid in a two-dimensional world is, obviously, a pair of coordinates X and Y, which denote the coordinates of the space of some given point of the body. The derivative for the coordinate vector is the velocity vector, and it shows us in which direction the point is moving (and the body, if we ignore the rotation, which is happening now) and how fast it is moving. The vector calculus is just the scalar calculus of each element of the vector, so the derivative of the X coordinate is the body velocity with respect to X, and so on. We introduce the following notation. Let the coordinate of the body be the vector r, and the velocity be the vector v or the vector r with a prime. We get the equation:
Equation 1
If we differentiate the velocity vector with respect to time, this will show how the coordinate vector changes with time. Acceleration is determined by analogy. This is the first derivative of speed or the second derivative of the coordinate vector:
Equation 2
The integral of acceleration gives us speed, and integrating acceleration twice, we get the coordinate.
These relationships in kinematics show that we can find the acceleration of an object, we can integrate it over time to get the speed and coordinate. As we will see later, we will turn to integration many times in our simulation code and will calculate a new position for our solid for each frame. Hooray animation!
Here is a simple example for a one-dimensional world that we can analytically integrate. Let's agree that we want to find the coordinate change from the end of the last frame to the time of the current frame to draw the current position. Next, we say that the acceleration of our solid was equal to 5 arbitrary units / second ^ 2. We will use the time elapsed from the end of the last frame as a variable t (in the integration element dt).
Equation 3
The above equations show that speed is a function of time elapsed from the last frame. We found the integration constant, C, which is equal to the initial velocity at the beginning of the integration period (at t = 0).
Equation 4
Now we integrate our velocity equation to find the coordinate (again, do not forget about the integration constant):
Equation 5
Based on Equation 5, we can find the current position only by a given acceleration if we know the initial coordinate and speed (which we will take from the last frame) and the elapsed time. The input variable is time, and the value of the function is the current position. We will also indicate the time in Equation 4 in order to calculate the final speed so that we can use this as the initial condition for the next frame.
May the force be with you
Now we have the realization that we need to set the acceleration correctly to integrate the kinematics equations in order to get the animation. The output of the speakers on stage. Remember, as I said, by pressing on something, you directly affect only the acceleration of the body? Well, “exerting pressure” is just a euphemism for the phrase “apply force” - one of the two key variables in dynamics - and now we can turn to Newton to find out how forces affect acceleration. Newton’s second law connects the force F with the derivative of the mass — the second magnitude of the dynamics — times velocity. The product of mass and speed is called the "momentum of the body", denoted by p:
Equation 6
Mass is a constant for the speeds we are working with now, this follows from the derivative in Equation 6, and we got the well-known equation F = ma (although I’m sure that Newton initially determined the force through the derivative of the momentum).
If we were dealing only with material points, Equation 6 is what we need in dynamics. For a given force of a given material point, acceleration is found by dividing the force by mass. This gives us acceleration, which will help solve the equation of motion from the example above. Nevertheless, we are dealing with solids with mass distributed over a certain area (volume, when it comes to the three-dimensional world), so we still need to work.
First, consider a solid as a set of point masses. We will define the total momentum, pT, for a solid, as the sum of the momenta of all the points that make up the body (I use the upper indexing, because I want to show more clearly what quantitative values belong to these points):
Equation 7
We can greatly simplify the analysis of the dynamics of a rigid body by introducing the concept of the center of mass (CM). A vector directed to the center of mass is a linear sum of vectors directed from all points of mass of a solid body divided by the mass of the whole body, M:
Equation 8
Using the definition of the center of mass, we can simplify Equation 7 by multiplying both sides of Equation 8 by M, differentiating them, and then substituting the result in Equation 7:
Equation 9
The right side of Equation 9 is the total momentum as defined in Equation 7. Now let's look at the left side of the equation: this is the speed at the center of mass multiplied by the mass of the whole body. Move the right side to the left and get:
Equation 10
From Equation 10 it follows that the linear momentum is equal to the total mass times the velocity directed from the center of mass, so there is no need to sum in Equation 7 in order to find the momentum if we know the mass of the body and the direction of the velocity vector of the center of mass. Further, all the final results of the calculations are finding the integrals for the whole body, but the center of mass exists and greatly simplifies the determination of the total momentum from Equation 10, so we can not worry - to find the linear momentum we can consider the body as a material point with given speed and mass.
By analogy, the total force is a derivative of the total momentum, so the concept of the center of mass can be used to simplify the equation of force:
Equation 11
In short, it follows from Equation 11 that we can consider all the forces interacting with a solid, as if their sum vector had an effect on the point of the center of mass, which contains the mass of the whole body. We divide the force (read gravity) by M in order to find the acceleration of the center of mass, and then integrate the acceleration in time in order to obtain the speed and coordinate of the body. Because we ignore the effects of rotation until the next article; we already have all the equations that we need to describe the dynamics of a rigid body. Note that Equation 11 does not contain information about where the forces applied to the body are directed. This will pop up when we deal with the linear momentum and the center of mass, and we just apply forces to the CM to find the acceleration of the center of mass.
Ode to Joy
At this stage, we can consider another example of analytical integration, using Equation 11 to find the acceleration of the center of mass instead of an arbitrarily chosen value = 5. Nevertheless, we face a serious problem, since analytical integration usually does not have an applied value, because it is too complicated, so we will focus on the so-called numerical integration of ordinary differential equations (ODEs). Wow, now that sounds like real math! Once you learn this, it will be time to raise the bar. Fortunately, the numerical integration of ODEs is not as difficult as it might seem at first glance! In order to understand what this means, we move from words to deeds!
So, a differential equation is an equation that contains derivatives of dependent quantities in addition to the function itself, independent variables and parameters. This is verbose, but here is an example for a time-varying force in a one-dimensional world: F = 2t, F is a dependent quantity, and t is independent. The value of F is determined only by F. Let the equation of force depend only on the speed of our body. The force of air resistance increases with increasing speed of the aircraft. Let us return to the example in the one-dimensional world, what if F = -v means that the friction force slows down our body in proportion to speed? We have a problem, because we solve the equation as follows: F = ma = -v and, dividing by m, we get (remember that acceleration is a derivative of speed):
Equation 12
This differential equation, (the velocity equation contains the velocity derivative in Equation 12) is called the ordinary differential equation, because it contains only ordinary derivatives of dependent quantities (as opposed to partial derivatives, which make up partial differential equations [PDEs], about which we are not will talk).
Now let's move on to the next part of our phrase: integration. How did we previously integrate dv / dt to find v in the conditions of this equation?
This will seem unbelievable, but almost every equation in physics is differential, so ODEs have been well studied. Differential equations can so often be found in physics, because often the rate of change of a quantitative quantity depends on the quantity itself. For example, we have already noted that braking (the magnitude of a change in speed), including the speed of air resistance, depends on speed. Other examples from physics: cooling (the rate of heat loss depends on the current temperature) and radioactive decay (decay rate depends on how much radioactive material is present).
The final word in our phrase - numerical - is our salvation. I say this because the theory of analytic integration of differential equations, even the simplest ones, is huge and rather confusing. Although, ironically, the integration of ODEs using computer numerical methods is actually relatively easy to understand. Next, I will describe a simple numerical integrator based on the Euler method, and will refine it in the next article.
Almost all numerical integrators, but no other one as explicit as the Euler method, are simply based on the old definition of computing through the first derivative of the slant: dy / dx determines the slope of y depending on x. For example, if we have the linear equation y = 5x, then dy / dx = 5 means that the slope is a constant equal to 5 for any x, and, as you can assume, this is a straight line. A slightly more difficult example is the parabola y = x2. In this case, dy / dx = 2x, and this is a function to determine the new slant for each x coordinate. I depicted y = x2 in Figure 2:

Figure 2. y = x2
In addition to this, I also hatched the direction of the vector oblique by solving the equation dy / dx = 2x + C for all x. Pay attention to the fact that the angle of the inclined vector is equal to the tangent of the tangent angle at this point. Note also that there are many different parabolas that satisfy the angle of the set of tangents, differing only in a shift along the y axis. Each of these parabolas is obtained by using different integration constants, which are contained in the equation dy / dx = 2x + C. The parabola that I pictured has an integration constant of 0. If I choose another constant, for example, 1, I get the equation y = 2x + 1. This means that there is a similar parabola with a shift of 1 unit up the y axis.
Now think about the fact that if you do not know the field of vectors in Figure 2 defined by a parabola, then just sit in a puddle. So, if you want to solve the tangent equation, you just need to follow the direction of the vector at each point, changing direction in accordance with the change in direction of the vector field. You will be surprised that after some time, you will see that you are moving along a parabolic trajectory (or along a section of the parabola), depending on where you started. Without realizing it, you integrated the equation of the vector field. You found a specific parabola (depending on where you started, or on the initial conditions), using only the derivative equation (calculating dy / dx as you move in the vector field).
Doing the same for a real differential equation is also simple. For a differential equation of the type dy / dx = f (x, y), finding the derivative dy / dx as tangent to f (x, y) describes the angle of inclination of the tangent for each coordinate on the x, y graph. If you are plotting a vector field given by dy / dx = f (x, y), you can follow this by analogy with a parabola by finding the derivative at each point and following in that direction. Figure 2 shows the vector field for Equation 12, our equation of air resistance, with velocity along the vertical axis and time along the horizontal (I arbitrarily chose m = 1 for this graph).

Figure 3. dv / dt = -v / m
It also shows one of the many possible curves. You may notice that if you choose the initial position in the graph (which depends on the initial speed in the equation), over time, the speed will tend to zero, because the friction force slows down the body. You can also see how the decrease in speed depends on the current value of speed - the faster you move, the faster it decreases. This becomes apparent when the same follows from Equation 12.
Numerical integration is similar to what we did on the chart. The Euler algorithm for numerical integration simply follows the vector field in accordance with the initial position by finding the derivative of the equation (-v / m for our example with the friction force) to determine the slope at the current point, and then simply moves forward step by step in time, depending on unchanged value of h, along the slope. Then a new position is calculated to determine the new slope after a certain time interval:
Or more precisely for our equation of air resistance:
Obviously, the Euler method gives a small error with each time step, since the real velocity vector (and therefore the solution curve) bends with a deviation at each point, and the Euler algorithm deviates slightly from the angle of inclination. But if the time step, h are rather small quantities, the error tends to zero. We will discuss this in more detail in the future.
This is all you need to know about numerical integration using the Euler method. You may ask how we are going to integrate the speed to get the coordinate. We simply use the Euler method again to integrate dr / dt = v, just as we integrated dv / dt = a, by analogy. We get two connected differential equations (one more of our victory):
This gives us an alternative algorithm for calculating the coordinate after the action of any arbitrarily applied force on our object (which may depend on the speed, as we saw, or time, or even the position of our body and other bodies, or all at once!). For the Euler method, it does not matter what the applied force looks like, because you can calculate it at any moment in time. Euler is interested in the magnitude of the effect of force on the mass, as inclined, and that’s it.
I ran out of space, so I have no way to provide links. Next time I will advise various wonderful books, and we will figure out how to calculate the rotation of solids.
And although his body is not as solid as we would like, Chris Hecker has a dynamic personality. If you apply force, he will answer e-mail checker@bix.com.
Translator's notes: a pun is presented here, the topic of the article and its content are played out.
PS The author of the translation expresses special thanks to the users of berez and MarazmDed for their editing of the translation. Thanks!
