Non-Mars Pyramids: Studying the Form of Nanocrystalline Clusters under a Graphene Layer

Very many properties, and therefore the methods of using something, depend on the shape of this object. Everything is very simple and just as logical: round wheels will roll better than square wheels, and the wings of an airplane have a certain shape that improves aerodynamics. Even ordinary pencils have the shape of a hexagon, so that it is more convenient to hold in your hand while writing and not to look for it throughout the apartment under all the sofas and cabinets in the pose of the person who first launched Dark Souls. Changing the shape can lead to a change in properties, and if these changes are controlled, then you can get certain properties that you need. This is exactly what scientists did in the study we are considering today. They created a “constant elasticity” model for nanocrystalline copper clusters under a graphene membrane. How and why did scientists “smear” copper with graphene, what results were shown by practical experiments, do they agree with preliminary calculations, and what does this “sandwich” on a nanometer scale mean for science? Answers to these questions await us in the report of the research group. Go.
Study basis
As the scientists themselves say, there is nothing more important than the structure and form of functional crystals (scientists have their own life priorities, we will not quibble). During the synthesis of these small objects, some deviations from the equilibrium structure are possible, which can be either a very unpleasant minus or a big plus. If you understand the very essence of the equilibrium structure, you can learn to better understand these structures, and, as a consequence, manipulate them.
An important role in this is played by nanocrystals (NCs), which are divided into several classes: unsupported three-dimensional nanocrystals obtained by liquid-phase synthesis, and supported three- and two-dimensional nanocrystals obtained by deposition on the substrate surface.
If we connect our favorite word “quantum” to all of this, then we will find out the following: for quantum dots, i.e. supported by three-dimensional NCs formed by lattice mismatch inside heteroepitaxy * , deformation plays an extremely important role in shape control.
Heteroepitaxy * is a type of epitaxy (the growth of one crystalline material on top of another at low temperatures), when the growing layer differs from the substrate in chemical composition.In this study, scientists consider a new type of three-dimensional nanocrystals (clusters), which are located under a layered material. Thus, these nanocrystals are compressed under one or several monolayers (above) and a set of semi-infinite layers (below).
Why do scientists do this, you ask. They will answer: the purpose of this study is to develop and analyze a model of constant elasticity (PE), which combines the deformation energy of the upper graphene layer, adhesion and surface energies of Cu (copper), graphene and graphite, which allows you to control the equilibrium shape of the surface / encapsulated clusters .
Scientists managed to create such a model, after which they tested its viability not on paper, but in reality. What results were shown by the analysis, and what discrepancies were observed between theory and practice, we will consider further.
Study preparation
At the very beginning, it was necessary to prepare graphite for interaction with copper nanoclusters. For this, defects were created on its surface by bombarding Ar +. After that, Cu atoms collided with the surface of graphite, penetrating some defects and were already below the surface of graphite. During this action, the graphite substrate is heated to 600-800 K. This temperature regime is chosen for a reason: the islands (clusters) of Cu on the graphite surface begin to coarsen at a temperature of 550-600 K, therefore, the breaking of the Cu-Cu bond should be easily achieved at 600 K and higher. As a result, islands of copper formed in this study at a temperature of 800 K.

Image No. 1
In the picture of STM 1awe see not the pyramids on the surface of the red planet, but the very islands of copper whose STM profile is shown on 1a ' .
Scientists direct our attention to the shape of this copper island: a flat-topped hexagon. The flattening of the top and, accordingly, the bottom indicates that the central part of the island is limited by the substrate layer (bottom) and the graphene layer (top). We also see slopes forming a ring around a flat top. According to observations, the thickness of the carbon layer on these islands can be several graphene monolayers, up to three.
Next, scientists analyzed the shape of this island ( 1b) It became clear that the height (h) scales almost identically with the width of the ring (a). Moreover, the slopes (h / a), that is, the slope of the sides, are constant at different sizes. But the diameter, in contrast to the width of the ring, scales poorly with height, that is, the aspect ratio d / h is not constant. Graph 1c shows the ratio of the height and width of the ring, and graph 1d shows the height and width of the tip of the island. At the same time, about 140 islands of copper were analyzed in total.
We are now clear about the real situation with copper nano formations under a layer of graphene. After these observations, scientists proceeded to create their model of constant elasticity (PE).
PE model
In the process of modeling, scientists decided to apply the approximation (approximation) of the shape of the island of copper, therefore, it was not the hexagonal pyramid that was used, but the cylindrical one. A copper cylinder grows between a membrane of one / several graphene monolayers and a graphite substrate.
It is assumed that the graphite substrate is rigid, and the covering layer (above the copper islands) undergoes elastic tensile and flexural deformations, which allows it to adapt to the growing island.
A small clarification of terms: in the future, in their work, scientists call the islands the aggregate of a Cu cluster, a deformed graphene membrane and a graphite substrate, and clusters - only the central metal part.
An important element of the shape of the islands are the slopes of the sides. These slopes are much smaller than that of the low-index (111) or (100) Cu planes, which naturally adjoin the upper face (111) for the supported Cu cluster. It follows from this that the annular space filled with copper is not an energetically viable configuration due to the surface with a high index and surface energy Cu.
Another important feature is the presence of folds of the ring, one of which can be seen in the lower left corner at 1a. Such deformations indicate that the membrane (covering layer) is not amenable to the influence of stretching of the underlying material, which limits its folding.
The energy of the system (Π) can be modeled as the sum of the elastic strain energies of the distorted graphene film (Ue ) and a set of variables representing the interface and surface (IS - interface / surface) components of the total energy of the system. Interfaces and surfaces include: pure copper, graphene - graphite (GnGt), copper - graphene and copper - graphite (the designation for both is CuG). The following IS energies correspond to the above:
- energy costs associated with the surface energy of Cu, U Cu and loss of adhesion Gn - Gt, U GnGt ;
- energy reduction associated with the adhesion of Cu - Gn and Cu - Gt, U GnGt .
Together, they will be referred to by the general term - U IS . The total energy formula is presented below:
Π = U Cu + U GnGt + U CuG + U e
The equilibrium form was obtained by minimizing Π for a fixed volume (V) of the Cu cluster.
Further, U IS , i.e., interface and surface components of the total energy of the system, were calculated . Each such component can be expressed as the sum of the products of surface energy (γ) or adhesion energy (β) multiplied by the corresponding area.

Table No. 1: formulas for calculating U IS (left) and input data (right).
The values of γ and β were obtained using the density functional theory. A (111) orientation of the Cu cluster was obtained from experimental data.
Then, the scientists deduced the U e value using the SLBT calculation model (blister test with a cylindrical rod with a flat top), in which the cylindrical rod moves up through the hole in a solid surface, pressing against the elastic membrane and deforming it.
The membrane undergoes tensile and flexural deformations. In the SLBT model, these two types of deformation are approximated as independent contributions. The calculations showed that the bending deformation is quite small when the size of the experimental structure is taken into account; therefore, modeling the total membrane elastic energy (U e ) was possible only with allowance for tensile strain.
The annular space can respond to island growth without restriction, but adhesion between the part of graphene at the top of the island and copper can prevent lateral extension of graphene. If the stretching proceeds freely, then this part can also freely deform over the top of the island.
Given this statement, the formula U e was derived (No. 5 in table 1). From it we can understand that the value of U e depends on the Poisson's ratio (v), the modulus of longitudinal elasticity (Y) and the thickness of the graphene (t). The value of v was 0.165, Y - 1.1 TPa, since this corresponds to the experimental values of the defect density (7.3 ± 0.4) x10 3 μm -2 .
Regarding the thickness of graphene, we already know that graphene on top of islands can be more than one monolayer thick. This allows us to calculate the thickness of the upper layer of the studied structure using the formula t = L · t GML , where L is the number of graphene layers and t GML is 0.34 nm (interlayer distance in crystalline graphite).
Research results
И так. С данными наблюдений разобрались, с расчетной частью тоже, пора приступить к результатам анализа всего этого в совокупности.
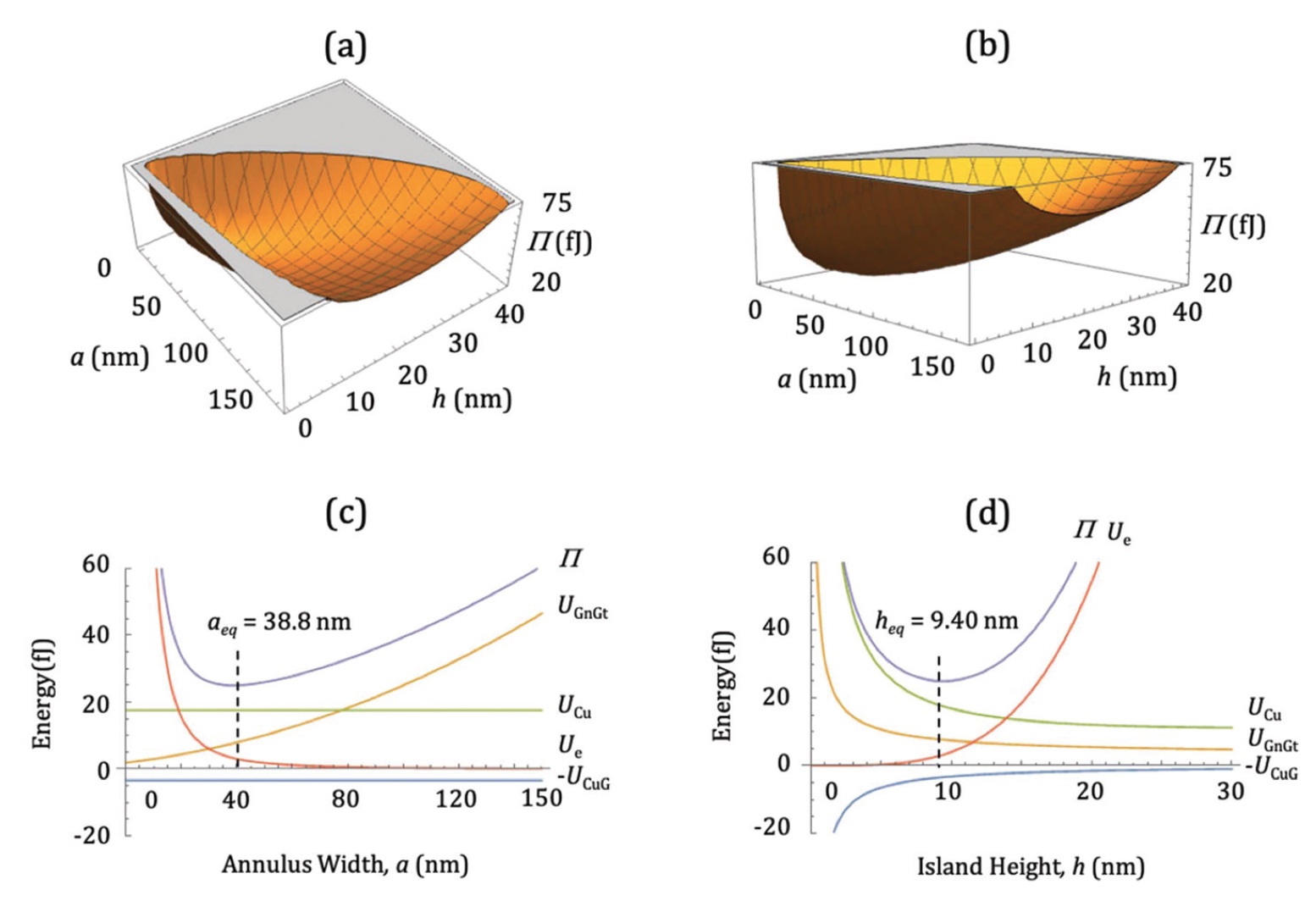
Учитывая формулы UIS и Ue, а также данные из таблицы 1 (справа), Π становится функцией только трех независимых параметров — a, h, и d. Эту проблему можно решить путем точного установления значения объема кластера V = πhd2/4, что позволяет ликвидировать либо h, либо d. Таким образом получится только два параметра, а не три: Π = Π(a, h) или Π = Π(a, d). Для демонстрации ученые использовали Π(a, h), а объем кластера был взят из используемых данных — 〈Vexp〉 = 4х104 нм3 (изображение №2).
Изображение №2
Scientists note an extremely important point: there is a certain minimum value of Π, which is a state of equilibrium. With such a minimum, the model of constant elasticity predicts the following values: a eq = 38.8 nm, h eq = 9.4 nm and d eq = 73.6 nm. In the experiments, the islands, which were close in terms of 〈V exp〉, had the following parameters: 〈a exp〉 = 31 ± 11 nm, 〈h exp〉 = 7.3 ± 2.6 nm, and 〈d exp〉 = 88 ± 21 nm. As we can see, the theoretical and practical data are in very good agreement.
Charts 2c and 2dshow two orthogonal sections through Π (a, h), each of which passes through a global minimum.
The above processes can be repeated over the entire range of experimentally observed cluster volumes (1.8 × 10 3 nm 3 ≤ V ≤ 6.9 × 5 5 nm 3 ). Therefore, it is possible to compare the sizes of islands predicted by the model and observed in experiments. For a simpler comparison of the model and experiment, the ratio of the sizes of the islands and the value of h is used (image No. 3).
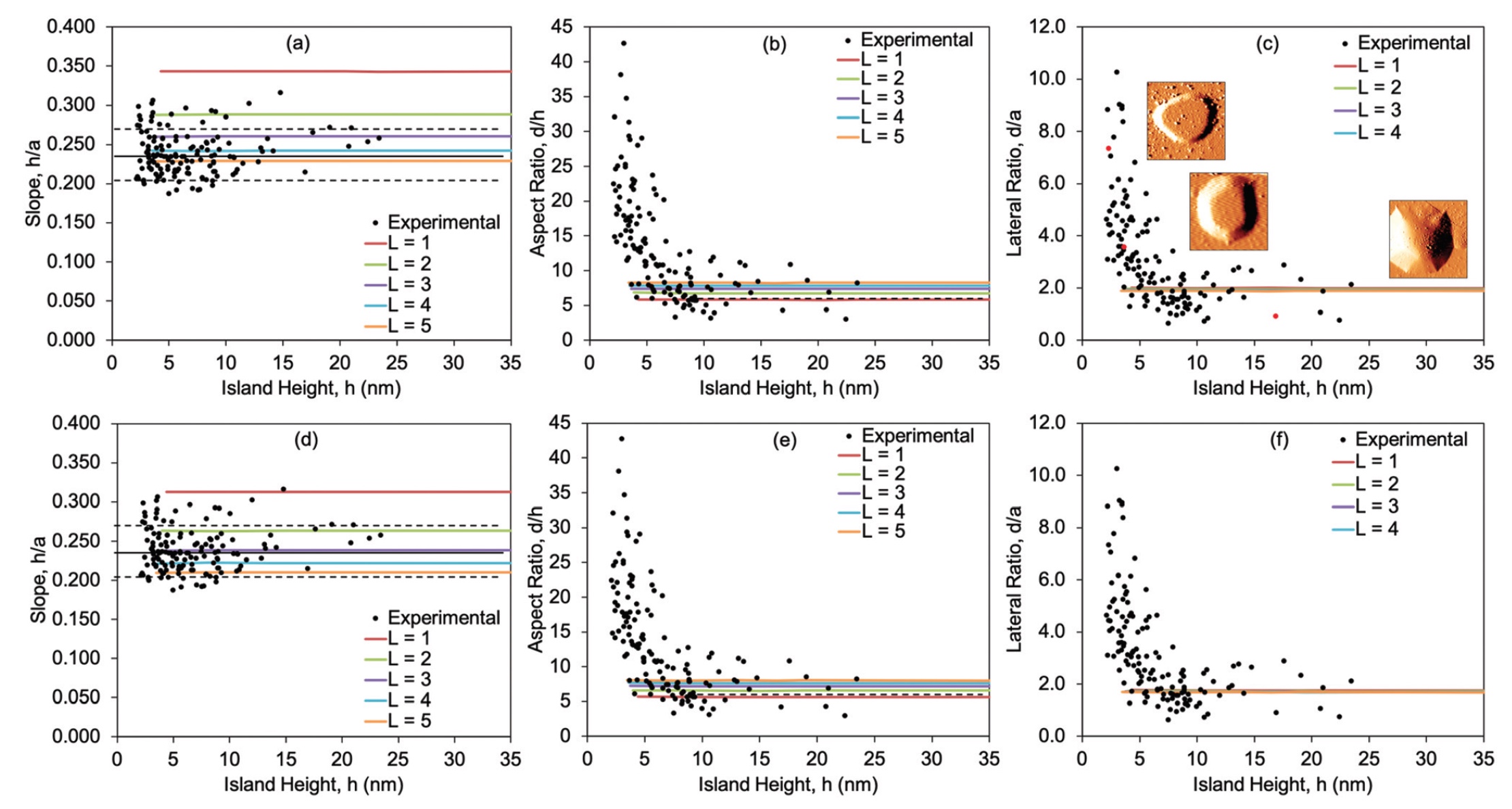
Image No. 3
The graphs above show the values of h / a, d / h and d / a for both the model and the experiment. Charts 3a - 3sthis is a comparison of experimental data and the SLBT model, in which membrane expansion proceeds without restrictions, and 3d - 3f is already experimental data and a model with limited expansion.
The h / a value in the experiments is constant and equals 0.24 ± 0.03 in the entire range of island sizes. In theory, the volume of clusters 1 ≤ L ≤ 5 was used, and the best agreement between the indicators of theory and practice was found at L = 4.
In the value of d / h (and parallel to d / a), unusual changes are observed. As can be seen from graph 3b, the experimental value of d / h starts at 40, but then begins to decrease sharply with increasing value of h. When h reaches ≈ 10 nm, the d / h value is equalized to 7.3 ± 2.8 (horizontal dashed line at 3b). The theoretical model showed d / h values in the range from 5.6 to 8.0 for L = 1 ... 5.
With a fixed SLBT model, performance is very similar to the free SLBT model. The only significant difference is that for any value of L, the h / a ratio in the fixed model is slightly less than in the free model. Thus, the best agreement between theory and practice in the case of a fixed SLBT model is manifested at L = 3.
For a more detailed study of the study, I strongly recommend that you look into the report of the research group .
Epilogue
What do we have in common? Scientists have created a theoretical model that is in excellent agreement with experimental data. This model demonstrates that the shape of nanocrystalline copper clusters persists, at least in the case of scales where the bending strain is not very strong. The researchers also found that delamination in the annular space is a reaction to the displacement of the membrane (covering layer) up exclusively in the central region (the inner circumference of the ring) and reflects the properties of graphene / graphite, and not copper itself.
In addition, it was found that similar observations described above are real for systems in which a metal cluster is embedded near the surface of a layered three-dimensional material or under a supported two-dimensional membrane, but only under the condition of an equilibrium shape. In this case, it is necessary (and possibly, as the results showed) to use the mechanical properties of the membrane, adhesion and surface energies to predict the equilibrium shape of the encapsulated body, that is, metal clusters (in this work copper). This principle also works in the opposite direction - one can find out the energy and mechanical properties by measuring cluster sizes. Scientists give a short example: by measuring h and a and knowing the mechanical properties of the membrane, it is possible to establish the adhesion energy of the membrane-substrate.
This work can best be used in modern technologies that rely on layered materials - graphite or its derivatives, like graphene. And if we take into account that the tendency toward a decrease in the physical dimensions of electronic devices is not yet declining, then such studies have a great price, and therefore we will wait for new shocking discoveries and amazing experiments.
Thank you for your attention, remain curious and have a good working week, guys!
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending it to your friends, a 30% discount for Habr users on a unique analogue of entry-level servers that was invented by us for you:The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to divide the server correctly? (options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps until the summer for free when paying for a period of six months, you can order here .
Dell R730xd 2 times cheaper? Only we have 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to Build Infrastructure Bldg. class using Dell R730xd E5-2650 v4 servers costing 9,000 euros for a penny?
