Google’s April Fool’s reverse engineering

Perhaps one of you noticed that on April 1, Google added the interactive game "Snake" to the Google Maps application for Android and iOS.

Check Point specialists are usually engaged in researching the latest cyber threats, but they were very interested in this game, however, they were very upset because of the losses ... so there was a logical thought: why not crack it!

Thus, our most mischievous employees began to think about the reverse development of the application using remote debugging. In general, they did it, and soon we successfully completed the task of never losing - and even added a simple AI that plays the game itself.





In this note, we describe in detail the hack.

First, we opened the application on the virtual device through Genymotion and launched the “Snake”, which is located in the menu in the upper right corner.

It seems that the game is displayed in WebView, so we started remote debugging in the Chrome developer tools:



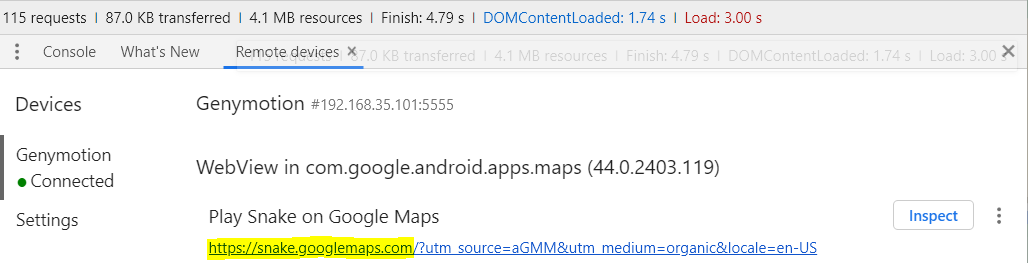
Then we went to the site and found the v18.js file on the source tab, and it had some interesting functions.

First, the fa () function initiates a 20 × 20 field:

this.height = this.width = 20;

Our main goal is to find and change a function that determines when a snake crashes into a wall or into itself to disable the possibility of losing. The width and height variables represent the dimensions of the playing field, so we looked for width and height inside the source code and found the F (a, b) function :



It looks like F (a, b) is checking if the coordinates of the snake's body are within the field. One option is to completely remove the conditions in the function so that it always returns the truth, thereby transferring us to the “God’s regime”, where we can pass through walls without dying.

To do this, we pressed the Inspect button in the remote console and changed the function F (a, b) to the following:



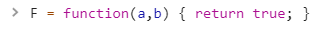
Now we can go through the walls:

Fig. 1. God Mode

This is all very good, but we still have to play, picking up people ourselves to earn points. The next hack will solve this problem.

There are many calls to wa (a) in the call stack . If we study this function, we will see that it is recursive and is responsible for querying animation frames. wa (a) calls the functions xa (a, b) and ya (a) , which display game pieces (train, people) and field, respectively.

Consider the function xa (a, b) :



It takes two arguments: 'a' and 'b'. The first is part of the global variable Q, which contains interesting information about our game, including an array that represents a playing field (Fig. 2), where we see a train (M), people and objects (K). The function also calculates the score and stores it in ci, which is also equivalent to Qb

Fig. 2. Array of the playing field

This array corresponds to such a field:


Fig. 3. The playing field

xa (a) also refers to the function sa (a) in Fig. 4, which generates random coordinates each time a new person is created. If you call the function more than once, you can create as many people as you want (Fig. 5).


Fig. 4. The function call sa (a)

Like here:


Fig. 5. Calling a function with creating any number of people on the map.

Note that even if you call sa (a) more than once and pick up a person, the score does not change. When selecting a passenger, the function ka (a, b) in Fig. 6. Thus, it needs to be changed so that with each call she adds 10 points and updates the score on the screen.


Fig. 6. Updated function The

coordinates of each part of the train are indicated in Qbob, where the first element is the first trailer in the train.


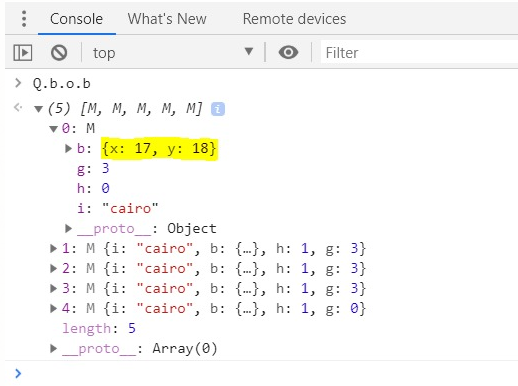
Fig. 7. Array of wagons

This will be needed to create a simple AI. Let's start with his logic:


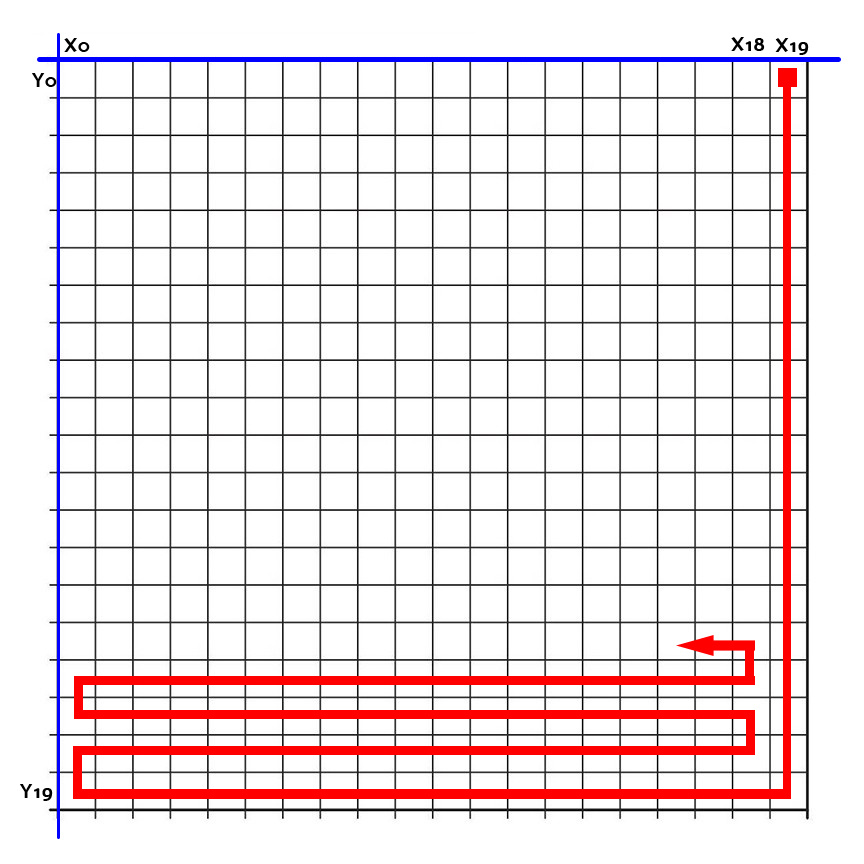
Fig. 8. The logic of AI

Snake is a state machine (state machine):

1. At X = 19, we go down until we get to Y = 19.
2. At X = 19 and Y = 19, go left to X = 0.
3. We pass to the state machine for zigzags:
   
   1. Up one cell and to the right to X = 18.
   2. Up one cell and left to X = 0.
   3. Back to step A.
4. At Y = 0, go right to X = 19.
5. Go back to step 1.

The full code is published on GitHub .

Video: