Monads in 15 minutes

Introduction

At the YOW! 2013 one of the developers of the Haskell language, prof. Philip Wadler showed how monads allow pure functional languages ​​to carry out essentially imperative operations, such as input-output and exception handling. Not surprisingly, the audience’s interest in this topic has generated explosive growth in publications about monads on the Internet. Unfortunately, most of these publications use examples written in functional languages, implying that newcomers to functional programming want to learn about monads. But monads are not specific to Haskell or functional languages, and may well be illustrated by examples in imperative programming languages. This is the purpose of this guide.

How is this guide different from the rest? We will try to open the monads in no more than 15 minutes using only intuition and a few elementary examples of Python code. Therefore, we will not begin to theorize and delve into philosophy, discussing burritos , space suits , desks and endofunctors.

Motivational examples

We will consider three issues related to composition of functions. We will solve them in two ways: the usual imperative and using monads. Then we compare the different approaches.

1. Logging

Let's say we have three unary functions f1, f2and f3taking a number and returns it increased by 1, 2, and 3, respectively. Each function also generates a message, which is a report on the completed operation.

def f1(x):
    return (x + 1, str(x) + "+1")
def f2(x):
    return (x + 2, str(x) + "+2")
def f3(x):
    return (x + 3, str(x) + "+3")

We would like to chain them to process the parameter x, in other words, we would like to calculate x+1+2+3. In addition, we need to get a human-readable explanation of what each function did.

We can achieve the result we need in the following way:

log = "Ops:"
res, log1 = f1(x)
log += log1 + ";"
res, log2 = f2(res)
log += log2 + ";"
res, log3 = f3(res)
log += log3 + ";"
print(res, log)

This solution is not ideal, as it consists of a large number of monotonous middleware. If we want to add a new function to our chain, we will be forced to repeat this linking code. In addition, manipulations with variables resalso logimpair the readability of the code, making it difficult to follow the main logic of the program.

Ideally, the program should look like a simple chain of functions, sort of f3(f2(f1(x))). Unfortunately, the data types returned by f1and f2do not match the types of f2and f3. But we can add new functions to the chain:

def unit(x):
    return (x, "Ops:")
def bind(t, f):
    res = f(t[0])
    return (res[0], t[1] + res[1] + ";")

Now we can solve the problem as follows:

print(bind(bind(bind(unit(x), f1), f2), f3))

The following diagram shows the computational process occurring at x=0. Here v1, v2and v3are the values ​​obtained as a result of calls to unitand bind.



The function unitconverts the input parameter xinto a tuple of a number and a string. The function bindcalls the function passed to it as a parameter and accumulates the result in an intermediate variable t.

We were able to avoid repeating middleware by placing it in a function bind. Now, if we have a function f4, we just include it in the chain:

bind(f4, bind(f3, ... ))

And we do not need to make any other changes.

2. List of intermediate values

We will also start this example with simple unary functions.

def f1(x): return x + 1
def f2(x): return x + 2
def f3(x): return x + 3

As in the previous example, we need to compose these functions in order to calculate x+1+2+3. Also, we need to get a list of all the values obtained as a result of our functions, ie x, x+1, x+1+2and x+1+2+3.

Unlike the previous example, our functions are composable, that is, the types of their input parameters coincide with the type of the result. Therefore, a simple chain f3(f2(f1(x)))will return us the final result. But in this case, we lose the intermediate values.

Let's solve the problem "head on":

lst = [x]
res = f1(x)
lst.append(res)
res = f2(res)
lst.append(res)
res = f3(res)
lst.append(res)
print(res, lst)

Unfortunately, this solution also contains a lot of middleware. And if we decide to add f4, we will again have to repeat this code to get the correct list of intermediate values.

Therefore, we add two additional functions, as in the previous example:

def unit(x):
    return (x, [x])
def bind(t, f):
    res = f(t[0])
    return (res, t[1] + [res])

Now we rewrite the program as a chain of calls:

print(bind(bind(bind(unit(x), f1), f2), f3))

The following diagram shows the computational process occurring at x=0. Again v1, v2and v3denote the values ​​obtained by calling unitand bind.

3. Empty values

Let's try to give a more interesting example, this time with classes and objects. Let's say we have a class Employeewith two methods:

class Employee:
    def get_boss(self):
        # Return the employee's boss
    def get_wage(self):
        # Compute the wage

Each class object Employeehas a leader (another class object Employee) and a salary, which are accessed through appropriate methods. Both methods can also return None(the employee does not have a manager, the salary is unknown).

In this example, we will create a program that shows the salary of the leader of this employee. If the manager is not found, or his salary cannot be determined, then the program will return None.

Ideally, we need to write something like

print(john.get_boss().get_wage())

But in this case, if any of the methods returns None, our program will end with an error.

An obvious way to handle this situation might look like this:

result = None
if john is not None and john.get_boss() is not None and john.get_boss().get_wage() is not None:
    result = john.get_boss().get_wage()
print(result)

In this case, we allow unnecessary method calls get_bossand get_wage. If these methods are heavy enough (for example, accessing the database), our solution will not do. Therefore, we change it:

result = None
if john is not None:
    boss = john.get_boss()
    if boss is not None:
        wage = boss.get_wage()
        if wage is not None:
            result = wage
print(result)

This code is optimal in terms of computing, but poorly read due to three nested ones if. Therefore, we will try to use the same trick as in the previous examples. Define two functions:

def unit(e):
    return e
def bind(e, f):
    return None if e is None else f(e)

And now we can put the whole solution in one line.

print(bind(bind(unit(john), Employee.get_boss), Employee.get_wage))

As you probably already noticed, in this case we did not have to write a function unit: it just returns the input parameter. But we will leave it so that it will be easier for us then to generalize our experience.

Note also that in Python we can use methods as functions, which allowed us to write Employee.get_boss(john)instead john.get_boss().

The following diagram shows the calculation process in the case when John does not have a leader, that is, john.get_boss()returns None.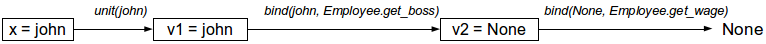

conclusions

Suppose we want to combine the same type of functions f1, f2, …, fn. If their input parameters are the same as the results, we can use a simple view chain fn(… f2(f1(x)) …). The following diagram shows a generic computing process with intermediate values designated as v1, v2, …, vn.



Often this approach is not applicable. The types of input values ​​and function results may vary, as in the first example. Or functions can be composable, but we want to insert additional logic between calls, as in examples 2 and 3 we inserted an aggregation of intermediate values ​​and a check for an empty value, respectively.

1. Imperative decision

In all the examples, we first used the most straightforward approach, which can be displayed in the following diagram:



Before the call, f1we performed some initialization. In the first example, we initialized a variable for storing a common log, in the second for a list of intermediate values. After that, we interspersed function calls with a certain connecting code: we calculated aggregate values, checked the result for None.

2. Monads

As we saw in the examples, imperative decisions always suffered from verbosity, repetition, and confusing logic. To get a more elegant code, we used a certain design pattern, according to which we created two functions: unitand bind. This template is called the monad . The function bindcontains linking code while it unitis initializing. This allows us to simplify the final solution to one line:

bind(bind( ... bind(bind(unit(x), f1), f2) ... fn-1), fn)

The calculation process can be represented by a diagram: The



call unit(x)generates an initial value v1. It then bind(v1, f1)generates a new intermediate value v2, which is used in the next call bind(v2, f2). This process continues until a final result is obtained. By defining various unitand bindwithin the framework of this template, we can combine various functions in one chain of calculations. Monad libraries ( for example, PyMonad or OSlash - approx. Transl. ) Usually contain ready-to-use monads (pairs of functions unitand bind) for implementing certain compositions of functions.

To chain functions, the values ​​returned unitand bindmust be of the same type as the input parametersbind. This type is called monadic . In terms of the above diagram, the type of variables v1, v2, …, vnto be monadic type.

Finally, consider how you can improve code written using monads. Obviously, repeating calls bindlook inelegant. To avoid this, define another external function:

def pipeline(e, *functions):
    for f in functions:
        e = bind(e, f)
    return e

Now instead

bind(bind(bind(bind(unit(x), f1), f2), f3), f4)

we can use the following abbreviation:

pipeline(unit(x), f1, f2, f3, f4)

Conclusion

Monads are a simple and powerful design pattern used to compose functions. In declarative programming languages, it helps to implement imperative mechanisms such as logging or input / output. In imperative languages,
it helps to generalize and shorten code that links a series of calls of functions of the same type.

This article provides only a superficial, intuitive understanding of monads. You can find out more by contacting the following sources:

1. Wikipedia
2. Monads in Python (with nice syntax!)
3. Monad tutorials timeline