Understanding convolutional neural networks through visualizations in PyTorch
In our era, machines have successfully achieved 99% accuracy in understanding and defining features and objects in images. We encounter this on a daily basis, for example: recognizing faces in the camera of smartphones, the ability to search for photos in google, scanning text from a barcode or books at good speed, etc. This efficiency of machines was made possible by a special type of neural network called convolutional neural network network. If you are an enthusiast of deep learning, you have probably heard of this, and you could have developed several image classifiers. Modern deep learning frameworks such as Tensorflow and PyTorch simplify machine learning for images. However, the question still remains: how does the data flow through the layers of the neural network and how does the computer learn from it? To get a clear view from scratch, we dive into convolution,

Before proceeding to the study of convolutional neural networks (SNS), you need to learn how to work with neural networks. Neural networks mimic the human brain to solve complex problems and find patterns in the data. Over the past few years, they have replaced many machine learning and computer vision algorithms. The basic model of a neural network consists of neurons organized in layers. Each neural network has an input and output layer and several hidden layers added to it depending on the complexity of the problem. When transferring data through layers, neurons learn and recognize signs. This representation of a neural network is called a model. After the model is trained, we ask the network to make predictions based on test data.
SNS is a special type of neural network that works well with images. Yang Lekun offered them in 1998, where they recognized the number present in the input image. SNAs are also used for speech recognition, image segmentation and text processing. Before creating convolutional neural networks, multilayer perceptrons were used in the construction of image classifiers. The classification of images refers to the task of extracting classes from a multichannel (color, black and white) bitmap. Multi-layer perceptrons take a long time to search for information in images, since each input must be connected to each neuron in the next layer. SNS bypassed them using a concept called local connectivity. This means that we connect each neuron to the local input area only. This minimizes the number of parameters, allowing different parts of the network to specialize in high-level features, such as texture or repeating patterns. Entangled? Let's compare how images are transmitted through multilayer perceptrons (MPs) and convolutional neural networks.
The total number of records in the input layer for a multilayer perceptron will be 784, since the input image has a size of 28x28 = 784 (the MNIST data set is considered). The network must be able to predict the number in the input image, which means that the output data may belong to any of the following classes in the range from 0 to 9. In the output layer, we return the class estimates, say, if the input is image number “3”, then in the output layer the corresponding neuron "3" has a higher value compared to other neurons. Again the question arises: “How many hidden layers do we need and how many neurons should there be in each?” For example, take the following MP code:
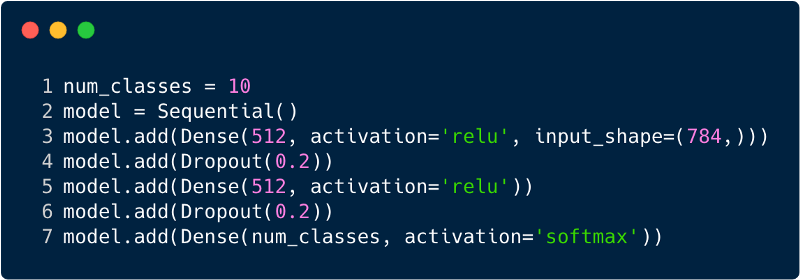
The code above is implemented using a framework called Keras. In the first hidden layer of 512 neurons that are associated with an input layer of 784 neurons. The next hidden layer: the exclusion layer, which solves the problem of retraining. 0.2 means that there is a 20% chance of not taking into account the neurons of the previous hidden layer. We again added a second hidden layer with the same number of neurons as in the first hidden layer (512), and then another exclusion layer. Finally, ending this set of layers with an output layer consisting of 10 classes. The class that has the highest value will be the number predicted by the model. This is how a multilayer network looks after determining all layers. One of the drawbacks of a multilevel perceptron is that it is fully connected, which takes a lot of time and space.
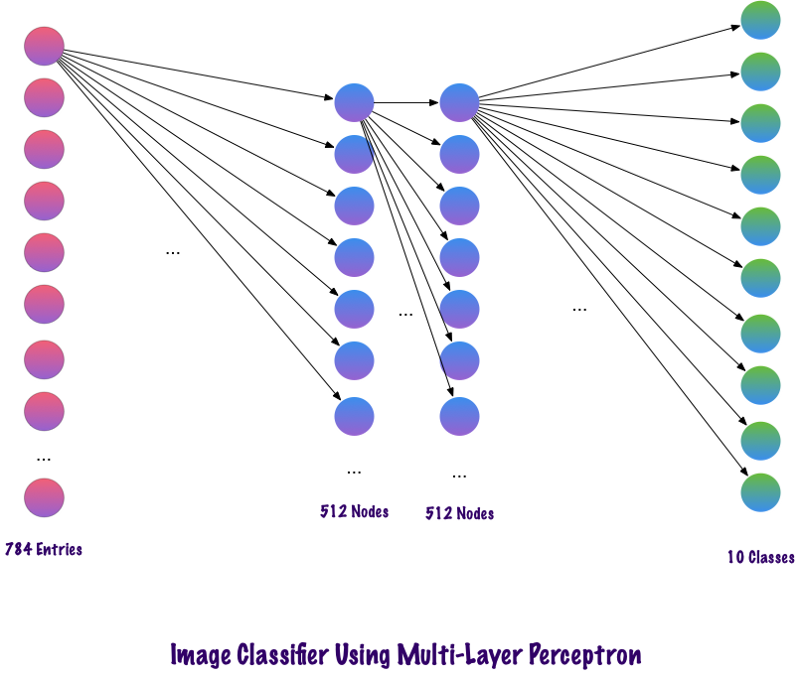
Convolutions do not use fully bound layers. They use sparse layers that take matrices as input, which gives an advantage over MP. In the MP, each node is responsible for understanding the whole picture. In the SNA, we divide the image into regions (small local areas of pixels). The output layer combines the received data from each hidden node to find patterns. Below is an image of how the layers are connected.
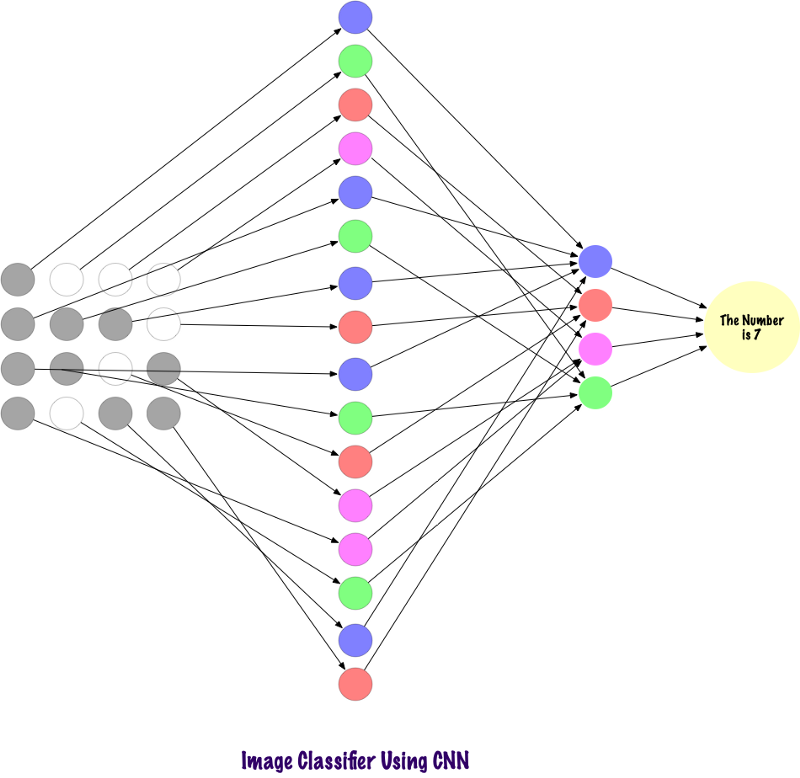
Now let's see how SNS find information in photos. Before this, we need to understand how signs are extracted. In the SNA, we use different layers, each layer retains the characteristics of the image, for example, it takes into account the image of the dog, when the network needs to classify the dog, it must identify all the signs, such as eyes, ears, tongue, legs, etc. These features are broken down and recognized at local network levels using filters and cores.
A person looking at an image and understanding its meaning sounds very reasonable. Let's say you walk, and notice the many landscapes around you. How do we understand nature in this case? We take pictures of the environment using our primary sense organ, the eye, and then send it to the retina. It all looks pretty interesting, right? Now let's imagine a computer doing the same thing. In computers, images are interpreted using a set of pixel values that lie in the range from 0 to 255. The computer looks at these pixel values and understands them. At first glance, he does not know the objects and colors. It simply recognizes the pixel values, and the image is equivalent to the set of pixel values for the computer. Later, by analyzing the pixel values, he gradually learns whether the image is gray or color. Images in grayscale have only one channel, since each pixel represents the intensity of one color. 0 means black, and 255 means white, the other options are black and white, that is, gray, are between them.
Color images have three channels, red, green and blue. They represent the intensity of 3 colors (three-dimensional matrix), and when the values change simultaneously, it gives a large set of colors, really a color palette! After that, the computer recognizes the curves and contours of objects in the image. All this can be studied in the convolutional neural network. For this, we will use PyTorch to load a dataset and apply filters to images. Below is a snippet of code.
Now let's see how a single image is fed into a neural network.

This is how the number “3” is broken down into pixels. From the set of handwritten digits, “3” is randomly selected, in which pixel values are displayed. Here ToTensor () normalizes the actual pixel values (0–255) and limits them to a range from 0 to 1. Why is this so? Because it facilitates the calculations in the following sections, either to interpret the images, or to search for common patterns that exist in them.
Filters, as the name implies, filter information. In the case of convolutional neural networks, when working with images, pixel information is filtered. Why should we filter at all? Remember that a computer must go through a learning process to understand images, very similar to how a child does it. In this case, however, we will not need many years! In short, he learns from scratch and then advances towards the whole.
Therefore, the network must initially know all the rough parts of the image, namely the edges, contours and other low-level elements. After they are discovered, a path is laid for complex signs. To get to them, we must first extract low-level signs, then medium, and then high-level signs. Filters represent a way to extract information that the user needs, and not just blind data transmission, due to which the computer does not understand the structuring of images. At the beginning, low-level functions can be extracted with a specific filter. The filter here is also a set of pixel values, similar to the image. It can be understood as weights that connect layers in a convolutional neural network. These weights or filters are multiplied by the input values to produce intermediate images, which represent computer image understanding. Then they are multiplied by several filters to expand the review. Then it detects the visible organs of a person (provided that there is a person in the image). Later, with the inclusion of several more filters and several layers, the computer exclaims: “Oh, yes! This is a man. "
If we talk about filters, then we have a lot of options. You may want to blur the image, then apply a blur filter, if you need to add sharpness, then a sharpness filter will come to the rescue, and so on.
Let's look at a few code snippets to understand the functionality of the filters.

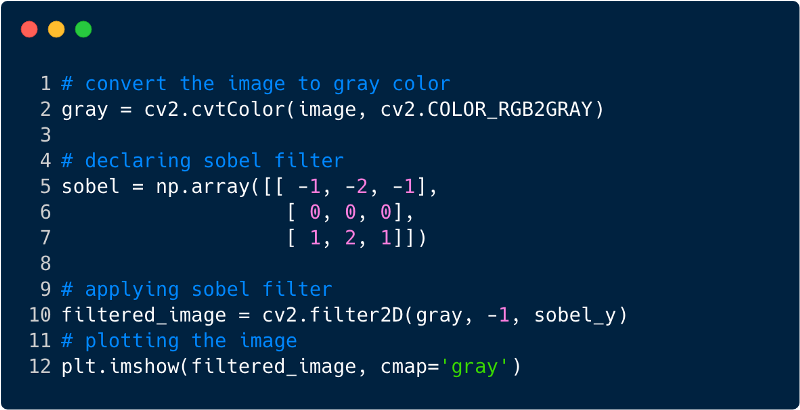

This is how the image looks after applying the filter, in this case we used the Sobel filter.
So far, we have seen how filters are used to extract features from images. Now, to complete the entire convolutional neural network, we need to know about all the layers that we use for its design. Layers used in SNS,
With all three layers, the convolutional image classifier looks like this:
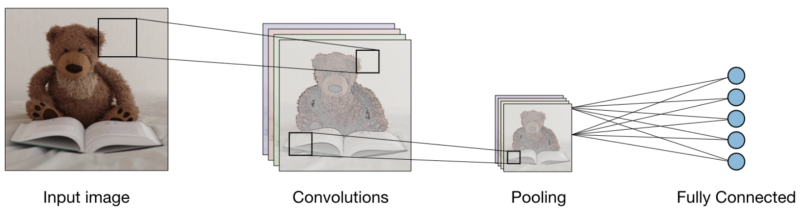
Now let's see what each layer does.
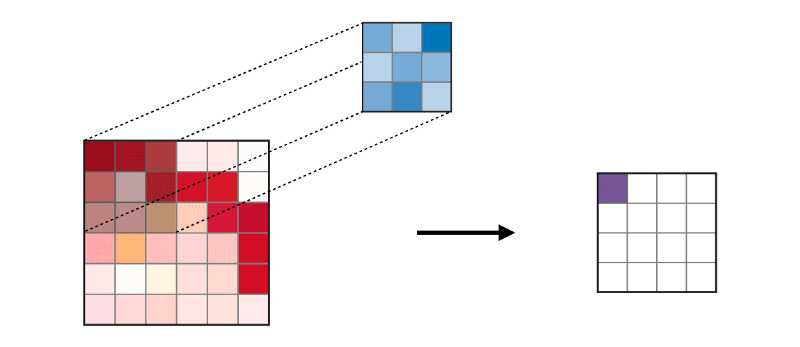
The convolution layer (CONV) uses filters that perform convolution operations by scanning the input image. Its hyperparameters include the size of the filter, which can be 2x2, 3x3, 4x4, 5x5 (but not limited to) and step S. The result O is called a feature map or activation map, in which all features are calculated using input layers and filters. Below is an image of the generation of feature maps when convolving is applied,
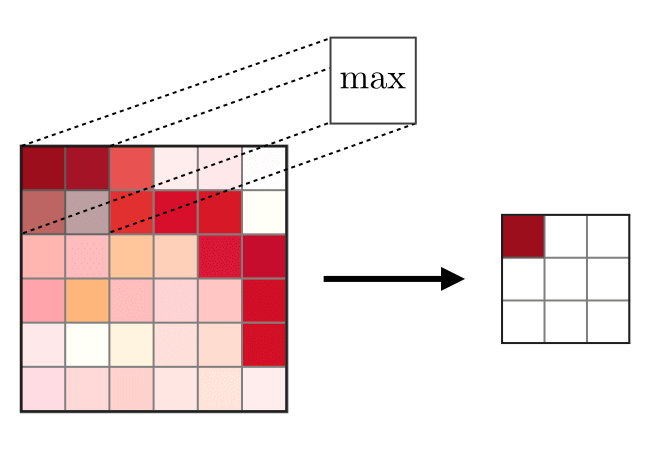
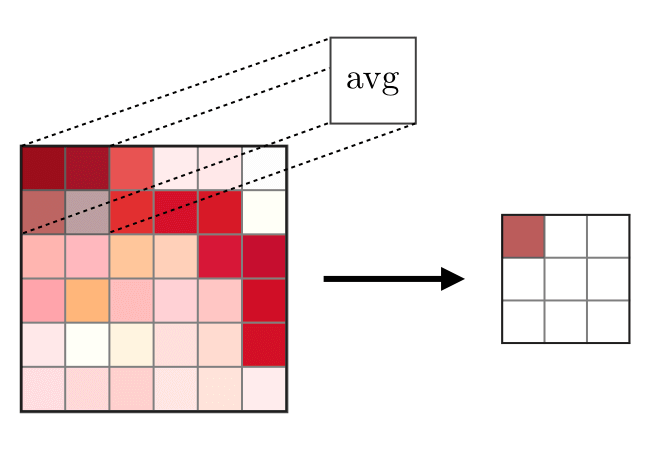
Merge Layer (POOL)used to seal traits commonly used after a layer of convolution. There are two types of join operations - the maximum and the average join, where the maximum and average values of features are taken, respectively. The operation of the join operations is shown below. The
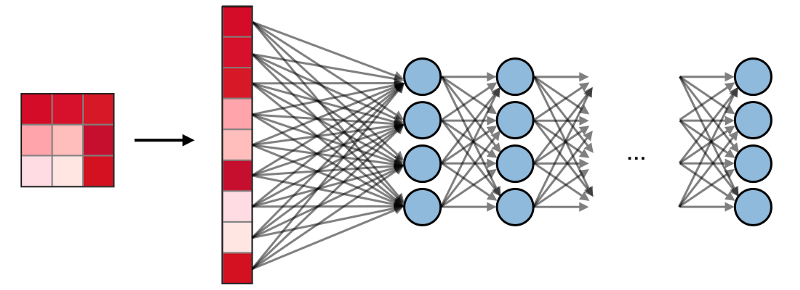
full-connected layers (FC) work with a flat entrance, where each input is connected with all neurons. They are usually used at the end of the network to connect hidden layers to the output layer, which helps to optimize class grades.
Now that we have a complete ideology for building SNS, let's implement SNS using the PyTorch framework from Facebook.
Step 1 : Download the input image to be sent via the network. (Here we do this using Numpy and OpenCV),

Step 2 : Visualizing the filters
Let's visualize the filters to better understand which ones we will use,

Step 3 : Definition of the SNA
This SNA has a convolutional layer and a layer of pooling with the maximum function, and the weights are initialized using the filters shown above,
quick look at the filters used,
Filters:

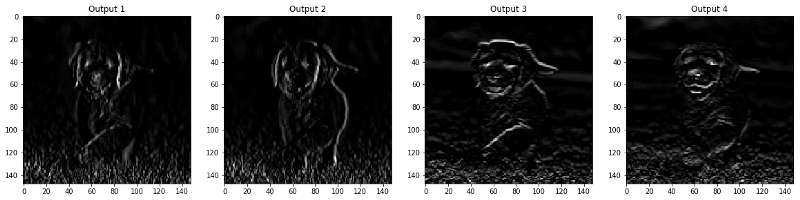
Step 5 : Filtered results by layers
The images that are output to the CONV and POOL layer are shown below,
Convolutional layers

Layers of pooling
Source

Convolutional neural networks
Before proceeding to the study of convolutional neural networks (SNS), you need to learn how to work with neural networks. Neural networks mimic the human brain to solve complex problems and find patterns in the data. Over the past few years, they have replaced many machine learning and computer vision algorithms. The basic model of a neural network consists of neurons organized in layers. Each neural network has an input and output layer and several hidden layers added to it depending on the complexity of the problem. When transferring data through layers, neurons learn and recognize signs. This representation of a neural network is called a model. After the model is trained, we ask the network to make predictions based on test data.
SNS is a special type of neural network that works well with images. Yang Lekun offered them in 1998, where they recognized the number present in the input image. SNAs are also used for speech recognition, image segmentation and text processing. Before creating convolutional neural networks, multilayer perceptrons were used in the construction of image classifiers. The classification of images refers to the task of extracting classes from a multichannel (color, black and white) bitmap. Multi-layer perceptrons take a long time to search for information in images, since each input must be connected to each neuron in the next layer. SNS bypassed them using a concept called local connectivity. This means that we connect each neuron to the local input area only. This minimizes the number of parameters, allowing different parts of the network to specialize in high-level features, such as texture or repeating patterns. Entangled? Let's compare how images are transmitted through multilayer perceptrons (MPs) and convolutional neural networks.
Comparison of MP and SNS
The total number of records in the input layer for a multilayer perceptron will be 784, since the input image has a size of 28x28 = 784 (the MNIST data set is considered). The network must be able to predict the number in the input image, which means that the output data may belong to any of the following classes in the range from 0 to 9. In the output layer, we return the class estimates, say, if the input is image number “3”, then in the output layer the corresponding neuron "3" has a higher value compared to other neurons. Again the question arises: “How many hidden layers do we need and how many neurons should there be in each?” For example, take the following MP code:

The code above is implemented using a framework called Keras. In the first hidden layer of 512 neurons that are associated with an input layer of 784 neurons. The next hidden layer: the exclusion layer, which solves the problem of retraining. 0.2 means that there is a 20% chance of not taking into account the neurons of the previous hidden layer. We again added a second hidden layer with the same number of neurons as in the first hidden layer (512), and then another exclusion layer. Finally, ending this set of layers with an output layer consisting of 10 classes. The class that has the highest value will be the number predicted by the model. This is how a multilayer network looks after determining all layers. One of the drawbacks of a multilevel perceptron is that it is fully connected, which takes a lot of time and space.

Convolutions do not use fully bound layers. They use sparse layers that take matrices as input, which gives an advantage over MP. In the MP, each node is responsible for understanding the whole picture. In the SNA, we divide the image into regions (small local areas of pixels). The output layer combines the received data from each hidden node to find patterns. Below is an image of how the layers are connected.

Now let's see how SNS find information in photos. Before this, we need to understand how signs are extracted. In the SNA, we use different layers, each layer retains the characteristics of the image, for example, it takes into account the image of the dog, when the network needs to classify the dog, it must identify all the signs, such as eyes, ears, tongue, legs, etc. These features are broken down and recognized at local network levels using filters and cores.
How do computers look at the image?
A person looking at an image and understanding its meaning sounds very reasonable. Let's say you walk, and notice the many landscapes around you. How do we understand nature in this case? We take pictures of the environment using our primary sense organ, the eye, and then send it to the retina. It all looks pretty interesting, right? Now let's imagine a computer doing the same thing. In computers, images are interpreted using a set of pixel values that lie in the range from 0 to 255. The computer looks at these pixel values and understands them. At first glance, he does not know the objects and colors. It simply recognizes the pixel values, and the image is equivalent to the set of pixel values for the computer. Later, by analyzing the pixel values, he gradually learns whether the image is gray or color. Images in grayscale have only one channel, since each pixel represents the intensity of one color. 0 means black, and 255 means white, the other options are black and white, that is, gray, are between them.
Color images have three channels, red, green and blue. They represent the intensity of 3 colors (three-dimensional matrix), and when the values change simultaneously, it gives a large set of colors, really a color palette! After that, the computer recognizes the curves and contours of objects in the image. All this can be studied in the convolutional neural network. For this, we will use PyTorch to load a dataset and apply filters to images. Below is a snippet of code.
# Load the librariesimport torch
import numpy as np
from torchvision import datasets
import torchvision.transforms as transforms
# Set the parameters
num_workers = 0
batch_size = 20# Converting the Images to tensors using Transforms
transform = transforms.ToTensor()
train_data = datasets.MNIST(root='data', train=True,
download=True, transform=transform)
test_data = datasets.MNIST(root='data', train=False,
download=True, transform=transform)
# Loading the Data
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers)
import matplotlib.pyplot as plt
%matplotlib inline
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy()
# Peeking into dataset
fig = plt.figure(figsize=(25, 4))
for image in np.arange(20):
ax = fig.add_subplot(2, 20/2, image+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[image]), cmap='gray')
ax.set_title(str(labels[image].item()))
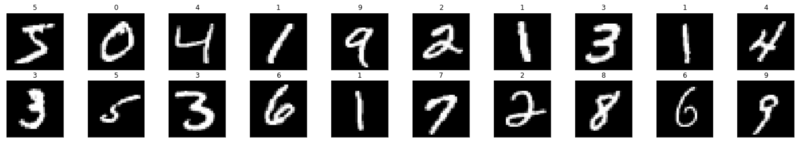
Now let's see how a single image is fed into a neural network.
img = np.squeeze(images[7])
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(111)
ax.imshow(img, cmap='gray')
width, height = img.shape
thresh = img.max()/2.5for x in range(width):
for y in range(height):
val = round(img[x][y],2) if img[x][y] !=0else0
ax.annotate(str(val), xy=(y,x),
color='white'if img[x][y]<thresh else'black')

This is how the number “3” is broken down into pixels. From the set of handwritten digits, “3” is randomly selected, in which pixel values are displayed. Here ToTensor () normalizes the actual pixel values (0–255) and limits them to a range from 0 to 1. Why is this so? Because it facilitates the calculations in the following sections, either to interpret the images, or to search for common patterns that exist in them.
Creating your own filter
Filters, as the name implies, filter information. In the case of convolutional neural networks, when working with images, pixel information is filtered. Why should we filter at all? Remember that a computer must go through a learning process to understand images, very similar to how a child does it. In this case, however, we will not need many years! In short, he learns from scratch and then advances towards the whole.
Therefore, the network must initially know all the rough parts of the image, namely the edges, contours and other low-level elements. After they are discovered, a path is laid for complex signs. To get to them, we must first extract low-level signs, then medium, and then high-level signs. Filters represent a way to extract information that the user needs, and not just blind data transmission, due to which the computer does not understand the structuring of images. At the beginning, low-level functions can be extracted with a specific filter. The filter here is also a set of pixel values, similar to the image. It can be understood as weights that connect layers in a convolutional neural network. These weights or filters are multiplied by the input values to produce intermediate images, which represent computer image understanding. Then they are multiplied by several filters to expand the review. Then it detects the visible organs of a person (provided that there is a person in the image). Later, with the inclusion of several more filters and several layers, the computer exclaims: “Oh, yes! This is a man. "
If we talk about filters, then we have a lot of options. You may want to blur the image, then apply a blur filter, if you need to add sharpness, then a sharpness filter will come to the rescue, and so on.
Let's look at a few code snippets to understand the functionality of the filters.




This is how the image looks after applying the filter, in this case we used the Sobel filter.
Convolutional neural networks
So far, we have seen how filters are used to extract features from images. Now, to complete the entire convolutional neural network, we need to know about all the layers that we use for its design. Layers used in SNS,
- Convolutional layer
- Pooling layer
- Fully connected layer
With all three layers, the convolutional image classifier looks like this:

Now let's see what each layer does.
The convolution layer (CONV) uses filters that perform convolution operations by scanning the input image. Its hyperparameters include the size of the filter, which can be 2x2, 3x3, 4x4, 5x5 (but not limited to) and step S. The result O is called a feature map or activation map, in which all features are calculated using input layers and filters. Below is an image of the generation of feature maps when convolving is applied,

Merge Layer (POOL)used to seal traits commonly used after a layer of convolution. There are two types of join operations - the maximum and the average join, where the maximum and average values of features are taken, respectively. The operation of the join operations is shown below. The


full-connected layers (FC) work with a flat entrance, where each input is connected with all neurons. They are usually used at the end of the network to connect hidden layers to the output layer, which helps to optimize class grades.

SNS Visualization in PyTorch
Now that we have a complete ideology for building SNS, let's implement SNS using the PyTorch framework from Facebook.
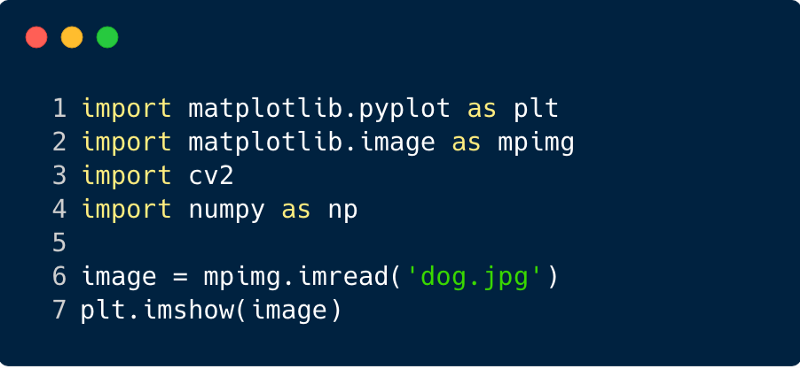
Step 1 : Download the input image to be sent via the network. (Here we do this using Numpy and OpenCV),
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
img_path = 'dog.jpg'
bgr_img = cv2.imread(img_path)
gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
# Normalise
gray_img = gray_img.astype("float32")/255
plt.imshow(gray_img, cmap='gray')
plt.show()

Step 2 : Visualizing the filters
Let's visualize the filters to better understand which ones we will use,
import numpy as np
filter_vals = np.array([
[-1, -1, 1, 1],
[-1, -1, 1, 1],
[-1, -1, 1, 1],
[-1, -1, 1, 1]
])
print('Filter shape: ', filter_vals.shape)
# Defining the Filters
filter_1 = filter_vals
filter_2 = -filter_1
filter_3 = filter_1.T
filter_4 = -filter_3
filters = np.array([filter_1, filter_2, filter_3, filter_4])
# Check the Filters
fig = plt.figure(figsize=(10, 5))
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
width, height = filters[i].shape
for x in range(width):
for y in range(height):
ax.annotate(str(filters[i][x][y]), xy=(y,x),
color='white'if filters[i][x][y]<0else'black')

Step 3 : Definition of the SNA
This SNA has a convolutional layer and a layer of pooling with the maximum function, and the weights are initialized using the filters shown above,
import torch
import torch.nn as nn
import torch.nn.functional as F
classNet(nn.Module):def__init__(self, weight):
super(Net, self).__init__()
# initializes the weights of the convolutional layer to be the weights of the 4 defined filters
k_height, k_width = weight.shape[2:]
# assumes there are 4 grayscale filters
self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False)
# initializes the weights of the convolutional layer
self.conv.weight = torch.nn.Parameter(weight)
# define a pooling layer
self.pool = nn.MaxPool2d(2, 2)
defforward(self, x):# calculates the output of a convolutional layer# pre- and post-activation
conv_x = self.conv(x)
activated_x = F.relu(conv_x)
# applies pooling layer
pooled_x = self.pool(activated_x)
# returns all layersreturn conv_x, activated_x, pooled_x
# instantiate the model and set the weights
weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor)
model = Net(weight)
# print out the layer in the network
print(model)
Step 4 : Filter Visualization ANet( (conv): Conv2d(1, 4, kernel_size=(4, 4), stride=(1, 1), bias=False) (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) )
quick look at the filters used,
defviz_layer(layer, n_filters= 4):
fig = plt.figure(figsize=(20, 20))
for i in range(n_filters):
ax = fig.add_subplot(1, n_filters, i+1)
ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray')
ax.set_title('Output %s' % str(i+1))
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05)
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
Filters:

Step 5 : Filtered results by layers
The images that are output to the CONV and POOL layer are shown below,
viz_layer(activated_layer)
viz_layer(pooled_layer)
Convolutional layers

Layers of pooling

Source
