May 15, 2019 at 12:03

Data Exchange and Differential Equations

    In one of the projects that I worked on, a mechanism for exchanging data between remote components of the system was implemented, working according to the following scenario: source component A, on its side, prepares data for transmission; component-receiver B periodically opens a communication session and takes all the data that A has accumulated at the time of connection. Data arriving already during a communication session is delayed until the next connection.

    At some point, I realized that the data transfer in such a scheme is described using an ordinary differential equation. Description of the model and the conclusions that were obtained with its help, under the cut.

    We denote$ x (t) $ - the amount of data in some arbitrary units accumulated for exchange on the side of component A by the time $ t $. Let the pause between the end of the exchange session and the beginning of the next equal$ a_0> 0 $ units of time, and for the transfer of one unit of data is required $ a_1> 0 $units of time. Then on the transfer$ x (t) $ data units required $ a_0 + a_1x (t) $units of time. Data rate is

    $ \ frac {x (t)} {a_0 + a_1x (t)}. \ quad (1) $


    If the data storage rate on side A is designated $ f (t) $then $ x (t) $ is a solution to the differential equation:

    $ \ frac {dx} {dt} = - \ frac {x} {a_0 + a_1x} + f (t). \ quad (2) $


    Since an unlimited growth in the volume of yet unsent data is an extremely undesirable situation, it becomes an important task to obtain conditions for the boundedness of solutions to this equation.

    For simplicity, we consider the function$ f (t) $continuous. Let be

    $ f (t) = \ phi_0 + \ phi (t), $


    Where

    $ \ left | \ int_0 ^ t \ phi (s) ds \ right | \ leq K _ {\ phi} <+ \ infty $


    for all $ t \ geq 0 $, a $ \ phi_0> 0 $- constant, playing the role of average value.

    Let's look at a few examples. Let be$ f (t) $ periodic and its schedule has the form:

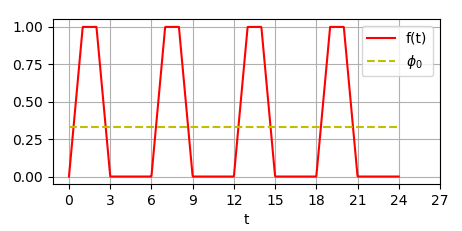
    image

    In this case $ \ phi_0 = 1/3 $, $ \ phi (t) = f (t) - \ phi_0 $.
    By numerically integrating equation (1) for several parameter values$ a_0, a_1 $ and initial values $ x (0) $, we obtain the following graphs of solutions:
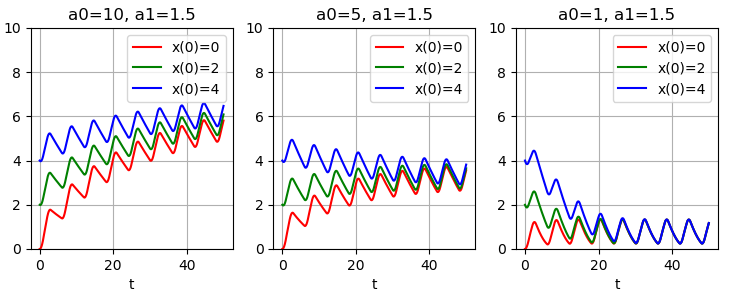
    image

    image

    The examples show: when $ 1 / a_1> \ phi_0 $, solutions are also limited for various values $ x (0) $the system tends to some steady state. Less shorter pauses between sessions$ a_0 $, the faster this convergence. At$ 1 / a_1 <\ phi_0 $such convergence is not observed, and solutions grow over time. Reducing the duration of pauses slows down the growth rate, but the tendency to an unlimited increase$ x (t) $still saved.

    In the general case, it can be shown that if$ 1 / a_1> \ phi_0 $, then the solutions of equation (1) are bounded, and if $ 1 / a_1 <\ phi_0 $- unlimited solutions will be obtained. That is, the limited solutions are determined only by the ratio of the rates of data accumulation and extraction. Duration of pauses between exchange sessions$ a_0 $, the only parameter that can be easily controlled does not fundamentally affect the behavior of the system. Although, as can be seen from relation (1) and the examples, with its increase, the exchange rate decreases.

    As a result, analysis of the model allows us to draw the following conclusions. If the exchange rate is insufficient, and the amount of data to send is constantly growing on the source side, then it makes no sense to try to correct the situation by reducing the pauses between sessions. Only an increase in system performance can help here.

    On the other hand, in the case when the exchange service constantly loads computers to the detriment of other tasks, the right decision will be to increase the pause duration within reasonable limits: this will only affect the relevance of the data, without the risk of overflowing the source with unsent data.

    Detailed calculations for the conditions of limited decisions and some other questions concerning the considered model are published in the materials of the school-seminar “Mathematical modeling, numerical methods and program complexes” named after E.V. Voskresensky. You can view and download the article here .
    Tags:

    Also popular now: