Whose triangle is thicker

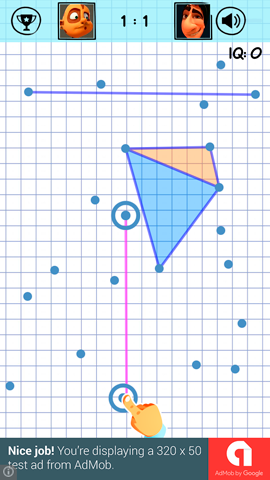
They asked to remove the publication from the castrated Habr and transfer here, which I do.

In addition to the genre, games have a form. This is like art - there are poems and even novels, but there are poems. Pushkin, for example, sometimes uploaded a dozen verses per week in the Appstore. And sometimes we plow no worse than a genius. Ah yes we are with Pushkin, oh yes sons of bitches!

One of the games written recently, it seemed to me worthy of the attention of the wide mathematical community, which adores geometric puzzles, competitions and self-irony.

Formulation of the problem

A random finite number of points are given on the plane.
Two players take turns.
In one move, the player can connect any two points in a straight line.
The line should not cross other shapes.

Purpose of the game

If, as a result of the move, a triangle is formed that does not contain other points inside itself, then the player receives a prize point.
The game ends when all the triangles are built.
You need to score more than the opponent.

Game modification

If, as a result of the move, a triangle is formed that does not contain other points inside itself, then the player adds the area of ​​the formed triangle to his asset.
It is necessary to conquer a larger area than the opponent.

Features of geometric implementation

For the initial location of the points, I crop the iPhone screen to a rectangle of 300 by 400 and make 10 pixels wide on the edges of the field.
I limit the distance between points to at least 16 pixels (for convenient finger grip).

The number of points is set randomly in the range from 12 to 30 pieces.

When building, I forbid to draw lines closer than 5 pixels to any points on the way.

Intelligence features

As an opponent, a processor from Apple. He plays in two states.
With a player rating of less than 25 points, Apple thinks one step ahead, randomly connecting the dots, if there is no option with an immediate point.
With a player rating of 25 points and above, the opponent thinks 2 moves ahead, checking the parity of the possibilities of constructing triangles obtained after the move.

During the development process, I increased the depth of the course to 10, after which the program went into a deep trance and fell in the face into the salad.

During the game, standard tricks were developed, with which you can sometimes win. I hope you find them yourself.

I did not build the mathematical theory of the game, but I considered the primitive layouts for the arrangement of 4 points.

Depending on the convexity of the 4-point pattern, if the game on both sides is optimal, the player who goes first plays either 2-0 wins or 1-2 loses.


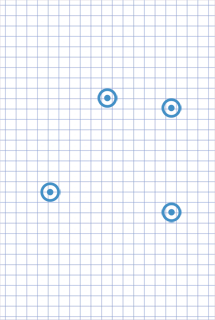
Convex pattern. The first player to win is 2-0.


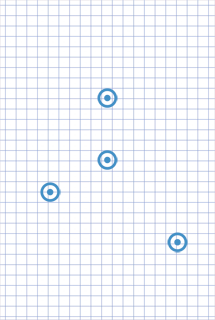
Convex pattern. The first player to lose is 1-2.

For a 5-point pattern, the first player always loses.

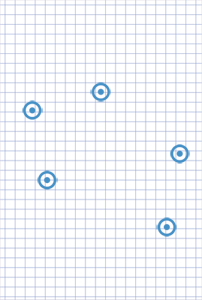
5 point convex pattern. The first player always loses.

The game sometimes resembles snooker in some way, when the opponent receives a move and cannot build a seemingly resulting triangle - other figures block.

Happy New Year to everyone - it is with a bonus! In 2016 - an extra day of life ...