Parallax: Deep Vision
- Transfer
How do we determine depth - the distance from our location to another object? There are several ways to do this, and one of the most common and easiest to understand includes such a geometric phenomenon as parallax . This extremely simple principle is used by our eyes and the brain to form our three-dimensional image of the world, and astronomers have used it for centuries to determine the distances (or relative distances) from Earth to astronomical objects.
Another common way to determine distances includes sending a wave (sound, light, something else), propagating at a known speed, which is reflected from the object and returns to us; the time taken to return the wave - the echo - tells us the distance to the object. By this principle, bats determine the distance to food and obstacles, and the radar also works.
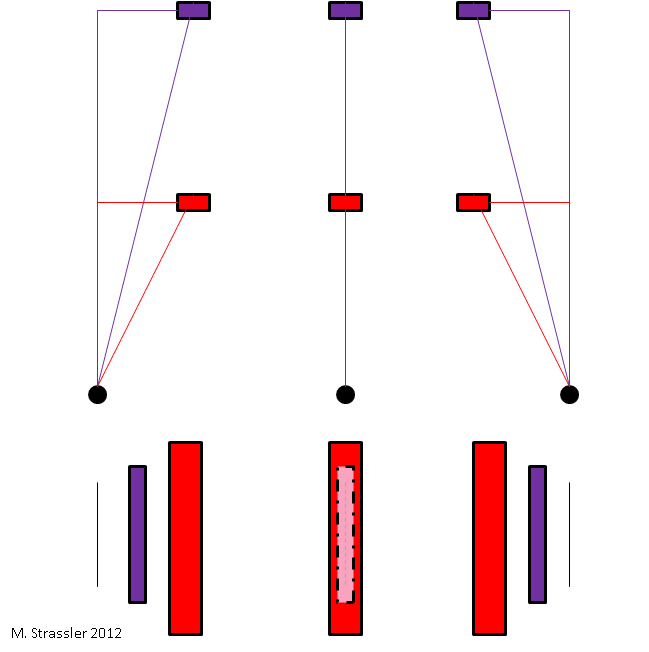
Fig. 1
We perceive parallax, without even thinking about it, every time we move our heads. Imagine what will happen if your friend hides from you, standing a few meters behind a large tree (Fig. 1, in the center). If you move far enough left or right, your friend will become visible (Fig. 1, left and right). We know that the whole thing is just in perspective; at a certain angle of view, the tree will no longer block your mysterious friend. Geometrically, what is happening is depicted in Fig. 1. When you move left and right, looking forward, nearby objects change their angle with respect to what is directly in front of you, faster than objects located further. From the rate of change of angle during your movement - from the parallax of movement - you can understand how far the object is located.
Every child knows this, because when you look out the window of a moving car, light poles pass by very quickly, distant buildings pass more slowly, and the moon, which is so far away that the angle of view with respect to the observer does not change by a noticeable amount while the car is traveling along the highway, as if moving with a car. It is a small parallax, which is the result of a great distance, that makes the moon "follow the car."
Everyone who watched old two-dimensional cartoons (and many modern ones), such as the Flintstones, know that this fact is used to portray depth. When characters travel in a car, moving from left to right, the car is drawn motionless, the trees are drawn in another layer, which moves from right to left at high speed, and the hills in the distance are drawn on the third layer, which moves from right to left a little slower (see Fig. 2) .

Fig. 2
Our ability to perceive depth without even moving our heads is based on the same principle. The left and right eyes see the world from slightly different angles. Try to place a couple of objects - no matter what, even if they are the thumbs - so that one of them is twice as far as the other, and is right behind it. Close your left eye and look at them with your right; then change your eyes; then change again, and do this several times - and you will see that the objects are moving, as in fig. 1, only your left eye will see the nearest object to the right of what's next, and the right eye will see it a little to the left.
So why do you perceive these objects with both eyes as if they are one after the other? Your optical system has a very tricky information processor - a kind of computer. For you, he does not create such a picture of the world as your eyes directly see, but a picture built on its basis with the help of complex transformations. The information obtained from two eyes and combined together allows you to perceive depth (this is mainly - although the parallax of movement also contributes). None of your eyes can determine the depth if you are standing still. Try closing your eyes, turning the other way, and opening one eye. Can you accurately describe the distance to objects? The world looks flatter, more two-dimensional than usual. With both eyes open you have no such problems.stereo effect .
But even with one eye open, you can quickly appreciate the depth if you move your head. Your brain is able to use the parallax of movement — a faster change in the angle of view of nearby objects relative to distant ones when moving left or right — to help restore some of the depth information that is usually obtained by comparing the view from two different eyes (Fig. 2).

Fig. 3
What basic calculations does our optical system use? The simplest case is shown in Fig. 3. Let's say the object is right in front of you. If your eyes are at a distance R from each other, and your left eye sees an object at an angle α to the right with respect to looking straight ahead, and your right eye sees an object at an angle α to the left, then according to the simplest geometry of right triangles, the distance D to the object will be dress
It can be seen from the formula that when D is smaller, the angle by which the line of sight of the object is distant from the direct view becomes larger. This is exactly what we expect from parallax.
In the more general case shown in Fig. 4, when the object is not directly in front of you, it turns out to be a little more complicated, like the trigonometric formulas, but the same basic principle works in it and as a result it is not so difficult to calculate. Your brain makes such calculations so quickly (using a technique that we have not yet disclosed) that you do not even suspect.
For objects far enough away, the angle α is too small for your eyes and brain to perceive. At this point, your sense of depth disappears. Therefore, the moon does not seem to be closer than the stars; they are too far away to feel the depth. Also, your sense of depth is usually not enough to understand whether the plane will pass in front of or behind a mountain in the distance. But this is just a restriction of your eyes.
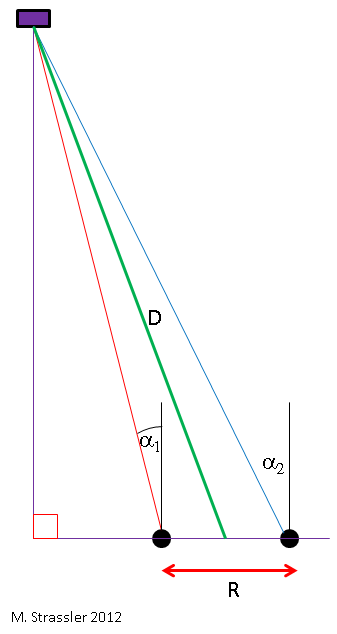
Fig. 4
How to determine the distance to more distant objects? There are two options; develop a scientific tool that can measure angles more accurately than your eye; increase R to compare not the view from the eyes, but, for example, the view from two cameras standing a few meters from each other, or even in different parts of the continent. And when astronomers want to measure the longest distances that can be measured using parallax, they compare the images of a distant star taken with a difference of six months to get the maximum distance R based on the fact that the Earth travels a fairly large distance during the year. The details of these techniques are different, but the basic principle is the same as the display in fig. 3 and fig. 4 - the principle of parallax.
Another common way to determine distances includes sending a wave (sound, light, something else), propagating at a known speed, which is reflected from the object and returns to us; the time taken to return the wave - the echo - tells us the distance to the object. By this principle, bats determine the distance to food and obstacles, and the radar also works.

Fig. 1
We perceive parallax, without even thinking about it, every time we move our heads. Imagine what will happen if your friend hides from you, standing a few meters behind a large tree (Fig. 1, in the center). If you move far enough left or right, your friend will become visible (Fig. 1, left and right). We know that the whole thing is just in perspective; at a certain angle of view, the tree will no longer block your mysterious friend. Geometrically, what is happening is depicted in Fig. 1. When you move left and right, looking forward, nearby objects change their angle with respect to what is directly in front of you, faster than objects located further. From the rate of change of angle during your movement - from the parallax of movement - you can understand how far the object is located.
Every child knows this, because when you look out the window of a moving car, light poles pass by very quickly, distant buildings pass more slowly, and the moon, which is so far away that the angle of view with respect to the observer does not change by a noticeable amount while the car is traveling along the highway, as if moving with a car. It is a small parallax, which is the result of a great distance, that makes the moon "follow the car."
Everyone who watched old two-dimensional cartoons (and many modern ones), such as the Flintstones, know that this fact is used to portray depth. When characters travel in a car, moving from left to right, the car is drawn motionless, the trees are drawn in another layer, which moves from right to left at high speed, and the hills in the distance are drawn on the third layer, which moves from right to left a little slower (see Fig. 2) .

Fig. 2
Our ability to perceive depth without even moving our heads is based on the same principle. The left and right eyes see the world from slightly different angles. Try to place a couple of objects - no matter what, even if they are the thumbs - so that one of them is twice as far as the other, and is right behind it. Close your left eye and look at them with your right; then change your eyes; then change again, and do this several times - and you will see that the objects are moving, as in fig. 1, only your left eye will see the nearest object to the right of what's next, and the right eye will see it a little to the left.
So why do you perceive these objects with both eyes as if they are one after the other? Your optical system has a very tricky information processor - a kind of computer. For you, he does not create such a picture of the world as your eyes directly see, but a picture built on its basis with the help of complex transformations. The information obtained from two eyes and combined together allows you to perceive depth (this is mainly - although the parallax of movement also contributes). None of your eyes can determine the depth if you are standing still. Try closing your eyes, turning the other way, and opening one eye. Can you accurately describe the distance to objects? The world looks flatter, more two-dimensional than usual. With both eyes open you have no such problems.stereo effect .
But even with one eye open, you can quickly appreciate the depth if you move your head. Your brain is able to use the parallax of movement — a faster change in the angle of view of nearby objects relative to distant ones when moving left or right — to help restore some of the depth information that is usually obtained by comparing the view from two different eyes (Fig. 2).

Fig. 3
What basic calculations does our optical system use? The simplest case is shown in Fig. 3. Let's say the object is right in front of you. If your eyes are at a distance R from each other, and your left eye sees an object at an angle α to the right with respect to looking straight ahead, and your right eye sees an object at an angle α to the left, then according to the simplest geometry of right triangles, the distance D to the object will be dress
It can be seen from the formula that when D is smaller, the angle by which the line of sight of the object is distant from the direct view becomes larger. This is exactly what we expect from parallax.
In the more general case shown in Fig. 4, when the object is not directly in front of you, it turns out to be a little more complicated, like the trigonometric formulas, but the same basic principle works in it and as a result it is not so difficult to calculate. Your brain makes such calculations so quickly (using a technique that we have not yet disclosed) that you do not even suspect.
For objects far enough away, the angle α is too small for your eyes and brain to perceive. At this point, your sense of depth disappears. Therefore, the moon does not seem to be closer than the stars; they are too far away to feel the depth. Also, your sense of depth is usually not enough to understand whether the plane will pass in front of or behind a mountain in the distance. But this is just a restriction of your eyes.

Fig. 4
How to determine the distance to more distant objects? There are two options; develop a scientific tool that can measure angles more accurately than your eye; increase R to compare not the view from the eyes, but, for example, the view from two cameras standing a few meters from each other, or even in different parts of the continent. And when astronomers want to measure the longest distances that can be measured using parallax, they compare the images of a distant star taken with a difference of six months to get the maximum distance R based on the fact that the Earth travels a fairly large distance during the year. The details of these techniques are different, but the basic principle is the same as the display in fig. 3 and fig. 4 - the principle of parallax.
