The power of known physical interactions
- Transfer
In this article I want to discuss the basic properties of the interactions known to us - four observables and the fifth - new - about whose existence we conclude from the discovery of the Higgs particle.
Specifically, I want to discuss what particle physics experts mean by describing interactions as weak or strong. You can meet such terminology often, but if no one has explained it to you, it is impossible to guess what it means. So here’s an explanation for you - although it’s a long one, but I hope it opens your eyes to how nature works, and also raises many new questions, which I hope to answer later.
What do these terms mean? In ordinary life, we would imagine that a strong interaction can lift us into the air, and we can cope with a weak one by straining our muscles a little. But experts in particle physics do not mean this at all.
Speaking of strengths and weaknesses, physicists do not mean the absolute strength or weakness of the interaction. It is not a question of whether the interaction can break the window or hold the gold bar. In this context, the terms “strong” and “weak” are not entirely absolute, in the sense in which we use them in everyday life or even in elementary school in physics. This terminology came about through a deep understanding of quantum field theory, a modern mathematical language used to describe known elementary particles and forces. But it is fundamental for the modern discussion of these problems by physicists. So I’ll start by justifying the reasons for the appearance of such terms.
Take a pair of objects of a certain type, for example, elementary particles, and place them at a distance r from each other. Suppose each has an effect on F on the other. Then we say that the impact is weak if
Where h is the Planck constant, c is the speed of light. Often in physics it is convenient to use not h, but
In short, in particle physics:
• For weak interactions
• For strong interaction
Usually, even in theoretical studies, we do not encounter interactions much stronger . Such power makes them so complex that we work with them in a different way. But this is a long story.
. Such power makes them so complex that we work with them in a different way. But this is a long story.
It turns out that this characteristic does not mean the absolute strength or weakness of the interaction, but whether it is strong or weak compared to typical interactions operating at a distance r. Not the interaction itself is taken into account; the interaction multiplied by the square of the distance is taken into account, and this value is compared with ℏ c.
To explain the usefulness of this concept, I will give an illustration for the case of electromagnetic interactions acting on simple charged particles - electrons, positrons and protons. The electric charge of electrons is –e; for protons and positrons, the charge is + e.
First, imagine two motionless protons, each with mass m and electric charge + e, located at a distance r from each other. The electric force pushes them to the sides, and its value is given by the formula
The same formula is applicable for two electrons with a charge –e. For an electron and a positron, the interaction will be the same, only it will attract them, and not push them apart.
What is k? This is the Coulomb constant , and its value depends on how to determine e, the basic unit of charge. But this is not important, because when discussing electrical interactions and elementary particles we will always see the joint appearance of ke 2 . We don’t need to know how big k is, we just need to know how big ke 2 is ?
It turns out that if r is greater than the millionth of a millionth of a meter, then ke 2approximately equals 0.007, multiply by (hc / 2π), where h is the Planck constant, and c is the speed of light. Therefore, we can write the electric force multiplied by r 2 as approximately equal
Since 0.007 is much less than 1, electromagnetism is a weak interaction, and remains so at all distances measured by us.
It is very important not to get confused! Just because electromagnetism is a weak interaction does not mean that the interaction of two protons is weak in absolute terms. In fact, the electric force trying to push away two protons in the helium nucleus can be compared with the weight of the truck! And all this power acts on two tiny particles! But for such small distances, this effect is rather weak, and a stronger interaction (“strong nuclear interaction”) resists electromagnetic repulsion, holding protons and neutrons in the helium core together.
By the way, for this value of 0.007 there is a historical name; it is called the fine structure constant (since it sets the size of small differences in the energies of various configurations of atoms), and usually denote α:
This is one of the most accurately measured quantities of nature. Often people write it approximately equal to 1/137 (and for many years some scientists thought that the number 137 was somehow special), but if you do it exactly, then you have to write 1 / 137.0359990 ...
So why is it the fact that α much less than 1, says that this interaction should be written in the weak, but not in the strong?
Why is it that α << 1 means that the electromagnetic interaction is weak?
It is easiest to show this by an example in which a force attracts particles - for example, an electron and a positron, or an electron and a proton. Starting with an electron and a positron is easier, because they have equal masses; they form an atomic state called positronium, similar to a hydrogen atom formed by an electron and a proton, but more symmetrical, in which two particles move in orbit around each other. In a hydrogen atom, an electron moves in an orbit around an almost motionless proton. In fact, the formulas for hydrogen are also suitable for positronium, with slight changes (differ by 2 times) in several places. (Yes, the electron and positron in positronium finally annihilate and turn into two or three photons, but only after the particles have many billions of revolutions - which, however, takes a small fraction of a second). For positronium in the state of least energy:
• the typical velocity of each particle is α / 2 × c;
• a typical energy of motion (kinetic) of each particle is equal to mc 2 × α 2 /8;
interaction energy (potential) of the two particles is -mc 2 × α 2 /2;
• B pozitroniuma binding energy (amount of movement and energy interaction energies) is equal to mc 2 × α 2 /4;
• positronium mass energy 2 mc 2 - B; and since the second is much smaller than the first, the mass of the atom is only slightly less than the sum of the masses of the electron and positron.
In short, due to the fact that α is much smaller than 1, there are three most important related facts:
• An electron and a positron move at speeds comparable to the speed of light c.
• Kinetic energy, potential energy, and binding energy B are small compared to the mass energy of an electron and positron, E = mc 2 .
• The mass of positronium is very close to the sum of the masses of the electron and positron.
All these statements are true regardless of how large or small the mass of the electron; they depend only on a small value of α.
All this together means that to describe this atom-like state, the Einstein special theory of relativity is not important. Newton's laws of motion are well suited to predictions, down to details not greater than α - that is, with an accuracy of 1% or better. And, as we will see later, this means that the system is relatively simple. It can be described using quantum mechanics with fairly simple mathematics, without the participation of quantum field theory, which would be necessary if SR were important. The mathematics of the hydrogen atom is the same as that of the positronium, and it is so simple that physicists get to know it at the institute, in the first lessons in quantum mechanics.
This can be thought of in another useful, albeit less well-known way. It must be remembered that electrons, like all elementary particles, are in reality quanta - tiny perturbations of quantum fields. They look more like waves than small balls. Accordingly, they vibrate, like all waves: they have a frequency of vibrations. The time that passes from one vibration to another — which I like to call poetically “heartbeat” —is hc / m. If α is small, then the time it takes for the light to cross the atomic state is much 1 / α longer than the heartbeat of the particles it contains. In this sense, positronium is quite large. And since the particles themselves move much slower than light, it takes even more time for the particles to cross this atomic state — something in the region of 1 / α 2heartbeats.
When α is small, other things that could be more complex are also simplified. For example, the action of a positron on an electron can cause an electron to turn into a virtual electron and a virtual photon - sometimes not for long. (Virtual “particles” are not particles; a real particle is a well-behaving wave of a quantum field, and a virtual one is a more general perturbation of these fields). But this rarely happens when α is small. Even less often, the virtual photon itself is indignant and turns into a virtual electron and positron. Because energy in the amount of 2mc 2, which is necessary to obtain a real electron and positron, there is nowhere to take (remember that the energies of motion and interactions are much less), virtual electron and positron appear very rarely. The fact that virtual particles rarely appear allows us to say that "the positronium atom consists of an electron and a positron" - that is exactly the way it is, most of the time. Only in very accurate calculations does one need to be more careful, and remember that this is not always the case. The same thing works for the hydrogen atom: it (almost all the time) is only one electron and one proton, held by a simple electrical interaction.
Now imagine that α gradually grows and approaches 1. What will happen to the positronium?

Fig. 1
With increasing α, the interaction (at any distance) between the electron and the positron becomes stronger, and since they are attracted more strongly, the particles in the atom-like state move closer. Particles move faster, approaching the speed of light. The energy of particle motion grows, the magnitude of the interaction energy grows, as does the binding energy - and approaches 2m. Accordingly, the mass of the atom-like state is no longer equal to about 2m. The size of the atomic state becomes smaller; the time required to intersect it with light, the time required to intersect it with particles, and the time elapsed between two heartbeats of particles begin to compare with each other.
Strengthening the interaction of an electron and a positron leads to a more frequent appearance of virtual photons; the presence of more energy in the atom facilitates the conversion of a virtual photon into a virtual electron and positron. When this happens, it becomes difficult to say which electron is real and which is virtual, because powerful forces act between the two electrons, as well as between the electron and any of the positrons. This can lead to the fact that the particle that was real becomes virtual, and makes the virtual particle real - and vice versa. Meanwhile, virtual electrons and positrons can also emit or absorb photons, which can be both virtual and real.
The very separation between real and virtual particles becomes more difficult to carry out. Real particles must be properly behaving perturbations of quantum fields. But the atom-like state is so small that only one heartbeat takes an electron and a positron to intersect it, and at that moment powerful interactions will already force them to change direction. How can we show that such a particle resembles a well-behaved perturbation? A well-behaved wave should be worried for a while - a few heartbeats - before external forces begin to influence it. And here our electron, although it looks more like a real particle than a virtual one, is still very distorted, and no longer fits the definition of a “real particle”. And this electron may not exist for long.
So, instead of the fact that we have small α - a simple system with a mass of slightly less than 2m, consisting of an electron and a positron moving with speeds much less than light - when α approaches 1, we find an extremely complex system in which many particles move with near-light speeds, with a mass very different from 2m (see Fig. 1). It is impossible to say how many particles are inside - will we only consider real ones? If so, how to accurately distinguish between almost real and almost virtual? The number of real particles can constantly change.
This is what characterizes a really strong interaction; objects formed by him are much more complicated than atoms. Scientists are in some ways lucky that the first objects encountered on the way to quantum field theory were atoms. They are held back by a weak interaction - electromagnetic force - and they were easy to understand with the help of simple mathematics of quantum mechanics, in which the number of particles is constant. The protons are held together by a strong interaction - a strong nuclear interaction. Therefore, it is not surprising that the structure of protons is much, much more complicated than that of atoms. The number of particles inside the proton is constantly changing - and this requires much more complex mathematics of quantum field theory.
By the way, the electrical interaction between two electrons is weak due to the fact that α is small. The same is true for interactions between two elementary particles, since the charges of all known particles are in the range from –e to e — for example, the charge of the upper quarks is 2/3 e. You may be interested in the interaction between the electron and the uranium nucleus, since the charge of the uranium nucleus is 92 e. Yes, in this case, the interaction is very strong! But in this case, only part of the effects that I describe for strong interactions is manifested, since changing the charge of only one of the interacting objects (in particular, heavy) does not increase the probability of detecting virtual electron-positron pairs. This will change only if the charge of the electron itself becomes much larger than e!
How strong are other known interactions of nature? We saw that in electrical interactions the force is equal to α - at least at the microscopic, atomic and subatomic level. And at such distances, up to the millionth of a millionths of a meter, α is constant. It does not depend on r, and in particular, therefore, is such a convenient measure. But in fact, the strength of the interaction can vary with distance, which complicates everything. For electromagnetism, this is not so important, this effect is very small. But for other forces, this is important.
The so-called weak nuclear interaction, of course, is weak. It is weak at the macroscopic, atomic and even nuclear level. But his strength is not constant. At distances greater than ℏ c / M W ~ 3 × 10 -18 meters (of the order of 1/300 of the proton radius), where MW = 80 GeV / c 2 - particle mass W, its strength α weak is approximately equal
Exhibitor makes this interaction surprisingly weak! Even at distances comparable with the size of the proton, this factor is already equal to e -300 , which means a decrease in its strength by so much that I can’t even write down this number here - it's 1 with 130 zeros. (This is more of a googol, units with a hundred zeros). And then this force quickly decreases further. Why? The same effect that gives the particle W (perturbation of the field W) mass makes impossible the perturbation of the field W at large distances, in contrast to the effect exerted by an electron or proton in an electric field. Accordingly, the influence of the field W does not work at large distances.
makes this interaction surprisingly weak! Even at distances comparable with the size of the proton, this factor is already equal to e -300 , which means a decrease in its strength by so much that I can’t even write down this number here - it's 1 with 130 zeros. (This is more of a googol, units with a hundred zeros). And then this force quickly decreases further. Why? The same effect that gives the particle W (perturbation of the field W) mass makes impossible the perturbation of the field W at large distances, in contrast to the effect exerted by an electron or proton in an electric field. Accordingly, the influence of the field W does not work at large distances.
But for even shorter distances
Please note that it is several times larger than the electromagnetic force! Weak interaction is not inherently weak at all - see fig. 2. Warning: I do not include here the subtleties associated with the interaction of weak and electromagnetic interactions at such small distances, as well as with a very slow change in force, which becomes noticeable at much smaller distances.
The weak interaction looks so weak, when observed on the example of the physics of nuclei, atoms and everyday life, the huge mass of the particle W. If the particle W had no mass, then the effect of the “weak” nuclear interaction would be stronger than that of the electric one! This is another context in which the Higgs field, giving the particle W its mass, plays an important role in our lives!
Strong nuclear interactions that attract and repel quarks and gluons (but not electrons) work very differently. At the distances that we discussed in the case of a weak nuclear interaction - 3 × 10 -18 meters - a strong nuclear interaction is much stronger than both weak and electromagnetic:
It is not particularly strong; it is about ten times weaker than a really strong interaction, and only ten times stronger than electromagnetism. In fact, although they differ greatly at macroscopic distances, the strong nuclear, weak nuclear and electromagnetic interactions differ from each other by only about 10 times at distances shorter than 3 × 10 -18 m. This is surprising, and probably not by chance. From there, to the idea of a “ great unification ” of these three forces, the step is quite small - it is believed that at much shorter distances all three interactions have the same force, and become parts of a more universal interaction.
But at large distances, strong nuclear interactions gradually become relatively strong. And again, I remind you what we mean by “weak” and “strong”; the interaction becomes weaker in absolute terms with increasing r, but compared with, say, electromagnetic interaction at the same distance, it becomes stronger.
This is very strong! And by the time r reaches 10 -15 m, the radius of the proton, α strong becomes more than 1 and it can no longer be determined in a unique way.
In short, strong nuclear interactions, which demonstrate moderate strength at distances much smaller than the proton radius, increase (in relative terms) with increasing distances, and become really strong at a distance of 10 -15 m (this is shown in Fig. 2). It is this really strong interaction that creates the proton and neutron, and the residual effect of this interaction combines these objects into the nucleus of an atom. Other important effects of enhancing this interaction are the conversion of high-energy quarks and gluons to hadron jets .
Why is the strong interaction gradually increasing with increasing r? I’ll tell you this some other time, but in fact, this is a very subtle effect that arises due to disturbances (virtual particles) in the fields of quarks and gluons, which are affected by strong interaction. The same effects affect the weak and electromagnetic interaction, but not so much, so I have not mentioned it before. For example, at a distance of 3 × 10 -18 m, the electromagnetic α becomes closer to 1/128 than to its value for large distances, equal to 1/137.
Given the strength of strong nuclear interaction, why don't we encounter it in everyday life? This is due to the subtleties of how it packs quarks, gluons and antiquarks so tightly into protons and neutrons that we never observe them separately. All this is very different from how a weak electromagnetic interaction allows electrons to easily escape from atoms, allowing phenomena such as static electricity (which includes lightning) and electric current (including through wires).
What about gravity? For the particles we know, gravity is surprisingly weak. For two motionless particles of mass m, gravity will have the value
Where G N is Newton's gravitational constant. Compare this with the electric force for which α = ke 2 / ℏ c. The roles of k and e of electric forces are played by G N and m. I note that I use Newton’s formula for gravity, but while α gravity is small compared to 1, the Einstein formula for attracting two objects will be essentially the same.
Now we rewrite the formula through the Planck mass M P = 10 19 GeV / s 2 , or of the order of the mass of 10 million million million protons, or 20 thousand million million million electrons. It is equal to about one tenth of a grain of salt.
So for two protons with a mass of 1 GeV / s 2, the gravitational interaction between them will be expressed by a square of 10 -19 :
This is a unit before which there are 37 zeros and a decimal separator! And for two electrons
Which, since the mass of an electron is about 2000 times smaller than the mass of a proton, is 4 million times weaker. Even for a pair of upper quarks, which are almost 200 times heavier than a proton, and whose mass is the largest among the masses of all known particles, the force of gravity will be equal
This is approximately 100,000,000,000,000,000,000,000,000,000,000 times less than the electrical interaction of the two upper quarks. Therefore, in fig. 2 gravity is not displayed.
If you think about it, this amazing weakness of gravity explains why you (using the electric forces that feed your muscles and hold your body) can move so freely, despite the fact that you are attracted by the whole vast Earth. This even explains how the Earth can be so many times larger than an atom; Gravity wants to compress the Earth, but the integrity of the atoms, whose electrical forces resist compression, prevents this. If gravitational forces were much stronger, or electric - weaker, gravity would compress the Earth to a much smaller size and much higher density.
Gravity is so weak that it is surprising that we even discovered it. Why did she become the first power known to people? Because it is the only force that survives over very long distances in ordinary matter.
• Weak nuclear interaction becomes extremely weak over long distances.
• Electromagnetism survives longer, and although this interaction is not very strong, it is enough to bind most of the electrons and atomic nuclei into electrically neutral combinations, whose electrically forces mutually destroy. For example, a hydrogen atom does not attract a distant electron, because an electron in a hydrogen atom repels it, and a proton in a nucleus attracts it, and these two forces are balanced.
• The strong nuclear interaction is so strong that it binds quarks, gluons, and antiquarks in combination, which also exhibit similar balancing effects.
• But there is nothing to balance gravity. There are no particles that create a gravitational interaction that repels matter, so you can not combine two particles so that their gravitational effect on distant objects is balanced.
Since 2012, we have a new food for thought: the interaction of particles caused by the Higgs field. Do not confuse it with the effect, due to which the Higgs field gives all known particles their masses; Higgs field can have this effect on a single, isolated particle. This is not an impact; it does not pull or push. But the Higgs field can also give rise to the interaction of two particles; this happens very much like electromagnetism. However, with ordinary matter, this effect is very, very difficult to detect. At short distances for particles such as electrons, and the upper and lower quarks that dominate the proton, the Higgs interaction is very weak (weaker than electromagnetism, but much stronger than gravity). At large distances, like the weak nuclear interaction, the Higgs interaction becomes extremely weak,
The Higgs field gives rise to an interaction similar to a weak nuclear interaction in that it has a very small exposure distance and that it becomes ineffective at distances greater than ℏ c / M h ~ 2 × 10 -18 m (1/500 proton radius ), where M h ≈ 125 GeV / c 2 , is the mass of the Higgs particle. At first glance, the formula is similar to the formula for gravity, since the attractive force is proportional to the masses of two elementary particles.
Where v = 246 GeV, this is the constant value of the Higgs field that exists in the entire Universe. (Actually, strictly speaking, there is another square root of 2 in the formula, but let's simplify to improve understanding).
But be careful! The similarity to gravity can be confusing. This formula works for well-known elementary particles - objects that receive their mass from the Higgs field. It works for electrons, muons and quarks. It does not work for protons, neutrons, atoms or you! Because the mass of the proton (and neutron, and therefore the atom, and therefore yours) is not completely generated by the Higgs field. This is different from the formula for gravity, which is true for all slow objects! Instead, in the case of ordinary atomic matter, we would need to replace the formula with a similar one, but with a different factor in front, its own for each atom. But qualitatively, the dependence on the distance would remain similar.
In addition, the formula I wrote assumes the existence of only one Higgs field and one Higgs particle (which has not yet been proved, but is the simplest possibility corresponding to the data obtained). If this is not so, the formula will become more complicated, although it will retain a similar form.
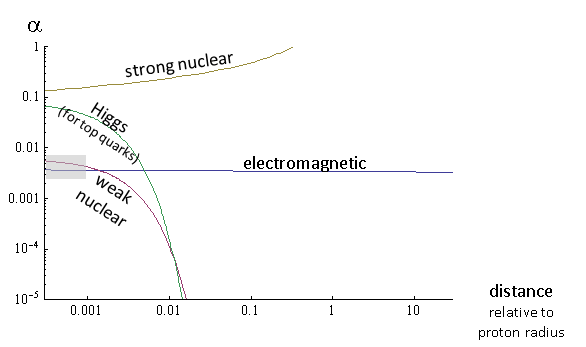
Fig. 2
How strong is this interaction? At very short distances, shorter than 2 × 10 -18m, the Higgs interaction for two quarks is comparable to the strong nuclear interaction at the same distance (see Fig. 2)! But in the case of electrons with a lower mass due to less interaction with the Higgs field, this interaction even at shorter distances will be much weaker than electric ones - more than a thousand million times weaker - although thousands of million million times stronger than the gravitational interaction of electrons . However, if we take two electrons in an atom that are ten million times farther apart from each other than 2 × 10 -18 m, then the Higgs interaction between them will be much, much smaller than even a tiny gravitational interaction, in e 10 000 000time. And even if the Higgs field were responsible for the entire mass of protons and neutrons, then the Higgs interaction in the nucleus would still be much weaker than gravity, which, in turn, is incredibly small compared to the strong nuclear interaction that holds parts of the nucleus.
It is the amazing weakness of the Higgs interaction in the context of ordinary matter that makes it so difficult to detect. On the other hand, the Higgs interaction, like gravity, always works on gravity, and is not balanced. But on the third hand, this does not matter, since, like the weak nuclear interaction, the Higgs interaction does not survive at long distances, since the Higgs particle, like the W particle, has mass. The interaction of Higgs at ultrashort distances is much stronger than gravity, but at nuclear and atomic distances it is much weaker due to the mass of the Higgs particle. And for the small particles of which we are composed, weakly interacting with the Higgs field, the Higgs interaction is always thousands of millions of times weaker than electric forces, even very small distances.
So, although every atom of the Earth interacts via Higgs with every other atom of the Earth, this force is so tiny, even for neighboring atoms, and especially for far-distant ones, that its effect cannot be detected. Therefore, we had to directly find the Higgs particle to confirm the existence of the Higgs field; we could not look for the force created by him in such a way as we can observe electric or magnetic forces and confirm in this way the existence of electric and magnetic fields.
When can we observe the effect of this force? Its effect will be detected for the first time either in the scattering of W and Z particles with each other (which sooner or later will be done, not directly, in proton collisions in the Large Hadron Collider) or in the interactions of the upper quark and the upper antiquark (which can be observed on the electron-positron collider - by the way, I wrote my first work on particle physics about this phenomenon).
Specifically, I want to discuss what particle physics experts mean by describing interactions as weak or strong. You can meet such terminology often, but if no one has explained it to you, it is impossible to guess what it means. So here’s an explanation for you - although it’s a long one, but I hope it opens your eyes to how nature works, and also raises many new questions, which I hope to answer later.
Weak versus Strong
What do these terms mean? In ordinary life, we would imagine that a strong interaction can lift us into the air, and we can cope with a weak one by straining our muscles a little. But experts in particle physics do not mean this at all.
Speaking of strengths and weaknesses, physicists do not mean the absolute strength or weakness of the interaction. It is not a question of whether the interaction can break the window or hold the gold bar. In this context, the terms “strong” and “weak” are not entirely absolute, in the sense in which we use them in everyday life or even in elementary school in physics. This terminology came about through a deep understanding of quantum field theory, a modern mathematical language used to describe known elementary particles and forces. But it is fundamental for the modern discussion of these problems by physicists. So I’ll start by justifying the reasons for the appearance of such terms.
Take a pair of objects of a certain type, for example, elementary particles, and place them at a distance r from each other. Suppose each has an effect on F on the other. Then we say that the impact is weak if
Where h is the Planck constant, c is the speed of light. Often in physics it is convenient to use not h, but
In short, in particle physics:
• For weak interactions
• For strong interaction
Usually, even in theoretical studies, we do not encounter interactions much stronger
It turns out that this characteristic does not mean the absolute strength or weakness of the interaction, but whether it is strong or weak compared to typical interactions operating at a distance r. Not the interaction itself is taken into account; the interaction multiplied by the square of the distance is taken into account, and this value is compared with ℏ c.
To explain the usefulness of this concept, I will give an illustration for the case of electromagnetic interactions acting on simple charged particles - electrons, positrons and protons. The electric charge of electrons is –e; for protons and positrons, the charge is + e.
First, imagine two motionless protons, each with mass m and electric charge + e, located at a distance r from each other. The electric force pushes them to the sides, and its value is given by the formula
The same formula is applicable for two electrons with a charge –e. For an electron and a positron, the interaction will be the same, only it will attract them, and not push them apart.
What is k? This is the Coulomb constant , and its value depends on how to determine e, the basic unit of charge. But this is not important, because when discussing electrical interactions and elementary particles we will always see the joint appearance of ke 2 . We don’t need to know how big k is, we just need to know how big ke 2 is ?
It turns out that if r is greater than the millionth of a millionth of a meter, then ke 2approximately equals 0.007, multiply by (hc / 2π), where h is the Planck constant, and c is the speed of light. Therefore, we can write the electric force multiplied by r 2 as approximately equal
Since 0.007 is much less than 1, electromagnetism is a weak interaction, and remains so at all distances measured by us.
It is very important not to get confused! Just because electromagnetism is a weak interaction does not mean that the interaction of two protons is weak in absolute terms. In fact, the electric force trying to push away two protons in the helium nucleus can be compared with the weight of the truck! And all this power acts on two tiny particles! But for such small distances, this effect is rather weak, and a stronger interaction (“strong nuclear interaction”) resists electromagnetic repulsion, holding protons and neutrons in the helium core together.
By the way, for this value of 0.007 there is a historical name; it is called the fine structure constant (since it sets the size of small differences in the energies of various configurations of atoms), and usually denote α:
This is one of the most accurately measured quantities of nature. Often people write it approximately equal to 1/137 (and for many years some scientists thought that the number 137 was somehow special), but if you do it exactly, then you have to write 1 / 137.0359990 ...
So why is it the fact that α much less than 1, says that this interaction should be written in the weak, but not in the strong?
Why is it that α << 1 means that the electromagnetic interaction is weak?
It is easiest to show this by an example in which a force attracts particles - for example, an electron and a positron, or an electron and a proton. Starting with an electron and a positron is easier, because they have equal masses; they form an atomic state called positronium, similar to a hydrogen atom formed by an electron and a proton, but more symmetrical, in which two particles move in orbit around each other. In a hydrogen atom, an electron moves in an orbit around an almost motionless proton. In fact, the formulas for hydrogen are also suitable for positronium, with slight changes (differ by 2 times) in several places. (Yes, the electron and positron in positronium finally annihilate and turn into two or three photons, but only after the particles have many billions of revolutions - which, however, takes a small fraction of a second). For positronium in the state of least energy:
• the typical velocity of each particle is α / 2 × c;
• a typical energy of motion (kinetic) of each particle is equal to mc 2 × α 2 /8;
interaction energy (potential) of the two particles is -mc 2 × α 2 /2;
• B pozitroniuma binding energy (amount of movement and energy interaction energies) is equal to mc 2 × α 2 /4;
• positronium mass energy 2 mc 2 - B; and since the second is much smaller than the first, the mass of the atom is only slightly less than the sum of the masses of the electron and positron.
In short, due to the fact that α is much smaller than 1, there are three most important related facts:
• An electron and a positron move at speeds comparable to the speed of light c.
• Kinetic energy, potential energy, and binding energy B are small compared to the mass energy of an electron and positron, E = mc 2 .
• The mass of positronium is very close to the sum of the masses of the electron and positron.
All these statements are true regardless of how large or small the mass of the electron; they depend only on a small value of α.
All this together means that to describe this atom-like state, the Einstein special theory of relativity is not important. Newton's laws of motion are well suited to predictions, down to details not greater than α - that is, with an accuracy of 1% or better. And, as we will see later, this means that the system is relatively simple. It can be described using quantum mechanics with fairly simple mathematics, without the participation of quantum field theory, which would be necessary if SR were important. The mathematics of the hydrogen atom is the same as that of the positronium, and it is so simple that physicists get to know it at the institute, in the first lessons in quantum mechanics.
This can be thought of in another useful, albeit less well-known way. It must be remembered that electrons, like all elementary particles, are in reality quanta - tiny perturbations of quantum fields. They look more like waves than small balls. Accordingly, they vibrate, like all waves: they have a frequency of vibrations. The time that passes from one vibration to another — which I like to call poetically “heartbeat” —is hc / m. If α is small, then the time it takes for the light to cross the atomic state is much 1 / α longer than the heartbeat of the particles it contains. In this sense, positronium is quite large. And since the particles themselves move much slower than light, it takes even more time for the particles to cross this atomic state — something in the region of 1 / α 2heartbeats.
When α is small, other things that could be more complex are also simplified. For example, the action of a positron on an electron can cause an electron to turn into a virtual electron and a virtual photon - sometimes not for long. (Virtual “particles” are not particles; a real particle is a well-behaving wave of a quantum field, and a virtual one is a more general perturbation of these fields). But this rarely happens when α is small. Even less often, the virtual photon itself is indignant and turns into a virtual electron and positron. Because energy in the amount of 2mc 2, which is necessary to obtain a real electron and positron, there is nowhere to take (remember that the energies of motion and interactions are much less), virtual electron and positron appear very rarely. The fact that virtual particles rarely appear allows us to say that "the positronium atom consists of an electron and a positron" - that is exactly the way it is, most of the time. Only in very accurate calculations does one need to be more careful, and remember that this is not always the case. The same thing works for the hydrogen atom: it (almost all the time) is only one electron and one proton, held by a simple electrical interaction.
What would happen if α were approximately equal to 1?
Now imagine that α gradually grows and approaches 1. What will happen to the positronium?

Fig. 1
With increasing α, the interaction (at any distance) between the electron and the positron becomes stronger, and since they are attracted more strongly, the particles in the atom-like state move closer. Particles move faster, approaching the speed of light. The energy of particle motion grows, the magnitude of the interaction energy grows, as does the binding energy - and approaches 2m. Accordingly, the mass of the atom-like state is no longer equal to about 2m. The size of the atomic state becomes smaller; the time required to intersect it with light, the time required to intersect it with particles, and the time elapsed between two heartbeats of particles begin to compare with each other.
Strengthening the interaction of an electron and a positron leads to a more frequent appearance of virtual photons; the presence of more energy in the atom facilitates the conversion of a virtual photon into a virtual electron and positron. When this happens, it becomes difficult to say which electron is real and which is virtual, because powerful forces act between the two electrons, as well as between the electron and any of the positrons. This can lead to the fact that the particle that was real becomes virtual, and makes the virtual particle real - and vice versa. Meanwhile, virtual electrons and positrons can also emit or absorb photons, which can be both virtual and real.
The very separation between real and virtual particles becomes more difficult to carry out. Real particles must be properly behaving perturbations of quantum fields. But the atom-like state is so small that only one heartbeat takes an electron and a positron to intersect it, and at that moment powerful interactions will already force them to change direction. How can we show that such a particle resembles a well-behaved perturbation? A well-behaved wave should be worried for a while - a few heartbeats - before external forces begin to influence it. And here our electron, although it looks more like a real particle than a virtual one, is still very distorted, and no longer fits the definition of a “real particle”. And this electron may not exist for long.
So, instead of the fact that we have small α - a simple system with a mass of slightly less than 2m, consisting of an electron and a positron moving with speeds much less than light - when α approaches 1, we find an extremely complex system in which many particles move with near-light speeds, with a mass very different from 2m (see Fig. 1). It is impossible to say how many particles are inside - will we only consider real ones? If so, how to accurately distinguish between almost real and almost virtual? The number of real particles can constantly change.
This is what characterizes a really strong interaction; objects formed by him are much more complicated than atoms. Scientists are in some ways lucky that the first objects encountered on the way to quantum field theory were atoms. They are held back by a weak interaction - electromagnetic force - and they were easy to understand with the help of simple mathematics of quantum mechanics, in which the number of particles is constant. The protons are held together by a strong interaction - a strong nuclear interaction. Therefore, it is not surprising that the structure of protons is much, much more complicated than that of atoms. The number of particles inside the proton is constantly changing - and this requires much more complex mathematics of quantum field theory.
By the way, the electrical interaction between two electrons is weak due to the fact that α is small. The same is true for interactions between two elementary particles, since the charges of all known particles are in the range from –e to e — for example, the charge of the upper quarks is 2/3 e. You may be interested in the interaction between the electron and the uranium nucleus, since the charge of the uranium nucleus is 92 e. Yes, in this case, the interaction is very strong! But in this case, only part of the effects that I describe for strong interactions is manifested, since changing the charge of only one of the interacting objects (in particular, heavy) does not increase the probability of detecting virtual electron-positron pairs. This will change only if the charge of the electron itself becomes much larger than e!
How weak is weak nuclear interaction? Complex issue…
How strong are other known interactions of nature? We saw that in electrical interactions the force is equal to α - at least at the microscopic, atomic and subatomic level. And at such distances, up to the millionth of a millionths of a meter, α is constant. It does not depend on r, and in particular, therefore, is such a convenient measure. But in fact, the strength of the interaction can vary with distance, which complicates everything. For electromagnetism, this is not so important, this effect is very small. But for other forces, this is important.
The so-called weak nuclear interaction, of course, is weak. It is weak at the macroscopic, atomic and even nuclear level. But his strength is not constant. At distances greater than ℏ c / M W ~ 3 × 10 -18 meters (of the order of 1/300 of the proton radius), where MW = 80 GeV / c 2 - particle mass W, its strength α weak is approximately equal
Exhibitor
But for even shorter distances
Please note that it is several times larger than the electromagnetic force! Weak interaction is not inherently weak at all - see fig. 2. Warning: I do not include here the subtleties associated with the interaction of weak and electromagnetic interactions at such small distances, as well as with a very slow change in force, which becomes noticeable at much smaller distances.
The weak interaction looks so weak, when observed on the example of the physics of nuclei, atoms and everyday life, the huge mass of the particle W. If the particle W had no mass, then the effect of the “weak” nuclear interaction would be stronger than that of the electric one! This is another context in which the Higgs field, giving the particle W its mass, plays an important role in our lives!
Strong nuclear interaction
Strong nuclear interactions that attract and repel quarks and gluons (but not electrons) work very differently. At the distances that we discussed in the case of a weak nuclear interaction - 3 × 10 -18 meters - a strong nuclear interaction is much stronger than both weak and electromagnetic:
It is not particularly strong; it is about ten times weaker than a really strong interaction, and only ten times stronger than electromagnetism. In fact, although they differ greatly at macroscopic distances, the strong nuclear, weak nuclear and electromagnetic interactions differ from each other by only about 10 times at distances shorter than 3 × 10 -18 m. This is surprising, and probably not by chance. From there, to the idea of a “ great unification ” of these three forces, the step is quite small - it is believed that at much shorter distances all three interactions have the same force, and become parts of a more universal interaction.
But at large distances, strong nuclear interactions gradually become relatively strong. And again, I remind you what we mean by “weak” and “strong”; the interaction becomes weaker in absolute terms with increasing r, but compared with, say, electromagnetic interaction at the same distance, it becomes stronger.
This is very strong! And by the time r reaches 10 -15 m, the radius of the proton, α strong becomes more than 1 and it can no longer be determined in a unique way.
In short, strong nuclear interactions, which demonstrate moderate strength at distances much smaller than the proton radius, increase (in relative terms) with increasing distances, and become really strong at a distance of 10 -15 m (this is shown in Fig. 2). It is this really strong interaction that creates the proton and neutron, and the residual effect of this interaction combines these objects into the nucleus of an atom. Other important effects of enhancing this interaction are the conversion of high-energy quarks and gluons to hadron jets .
Why is the strong interaction gradually increasing with increasing r? I’ll tell you this some other time, but in fact, this is a very subtle effect that arises due to disturbances (virtual particles) in the fields of quarks and gluons, which are affected by strong interaction. The same effects affect the weak and electromagnetic interaction, but not so much, so I have not mentioned it before. For example, at a distance of 3 × 10 -18 m, the electromagnetic α becomes closer to 1/128 than to its value for large distances, equal to 1/137.
Given the strength of strong nuclear interaction, why don't we encounter it in everyday life? This is due to the subtleties of how it packs quarks, gluons and antiquarks so tightly into protons and neutrons that we never observe them separately. All this is very different from how a weak electromagnetic interaction allows electrons to easily escape from atoms, allowing phenomena such as static electricity (which includes lightning) and electric current (including through wires).
Gravity
What about gravity? For the particles we know, gravity is surprisingly weak. For two motionless particles of mass m, gravity will have the value
Where G N is Newton's gravitational constant. Compare this with the electric force for which α = ke 2 / ℏ c. The roles of k and e of electric forces are played by G N and m. I note that I use Newton’s formula for gravity, but while α gravity is small compared to 1, the Einstein formula for attracting two objects will be essentially the same.
Now we rewrite the formula through the Planck mass M P = 10 19 GeV / s 2 , or of the order of the mass of 10 million million million protons, or 20 thousand million million million electrons. It is equal to about one tenth of a grain of salt.
So for two protons with a mass of 1 GeV / s 2, the gravitational interaction between them will be expressed by a square of 10 -19 :
This is a unit before which there are 37 zeros and a decimal separator! And for two electrons
Which, since the mass of an electron is about 2000 times smaller than the mass of a proton, is 4 million times weaker. Even for a pair of upper quarks, which are almost 200 times heavier than a proton, and whose mass is the largest among the masses of all known particles, the force of gravity will be equal
This is approximately 100,000,000,000,000,000,000,000,000,000,000 times less than the electrical interaction of the two upper quarks. Therefore, in fig. 2 gravity is not displayed.
If you think about it, this amazing weakness of gravity explains why you (using the electric forces that feed your muscles and hold your body) can move so freely, despite the fact that you are attracted by the whole vast Earth. This even explains how the Earth can be so many times larger than an atom; Gravity wants to compress the Earth, but the integrity of the atoms, whose electrical forces resist compression, prevents this. If gravitational forces were much stronger, or electric - weaker, gravity would compress the Earth to a much smaller size and much higher density.
Gravity is so weak that it is surprising that we even discovered it. Why did she become the first power known to people? Because it is the only force that survives over very long distances in ordinary matter.
• Weak nuclear interaction becomes extremely weak over long distances.
• Electromagnetism survives longer, and although this interaction is not very strong, it is enough to bind most of the electrons and atomic nuclei into electrically neutral combinations, whose electrically forces mutually destroy. For example, a hydrogen atom does not attract a distant electron, because an electron in a hydrogen atom repels it, and a proton in a nucleus attracts it, and these two forces are balanced.
• The strong nuclear interaction is so strong that it binds quarks, gluons, and antiquarks in combination, which also exhibit similar balancing effects.
• But there is nothing to balance gravity. There are no particles that create a gravitational interaction that repels matter, so you can not combine two particles so that their gravitational effect on distant objects is balanced.
Higgs interaction?
Since 2012, we have a new food for thought: the interaction of particles caused by the Higgs field. Do not confuse it with the effect, due to which the Higgs field gives all known particles their masses; Higgs field can have this effect on a single, isolated particle. This is not an impact; it does not pull or push. But the Higgs field can also give rise to the interaction of two particles; this happens very much like electromagnetism. However, with ordinary matter, this effect is very, very difficult to detect. At short distances for particles such as electrons, and the upper and lower quarks that dominate the proton, the Higgs interaction is very weak (weaker than electromagnetism, but much stronger than gravity). At large distances, like the weak nuclear interaction, the Higgs interaction becomes extremely weak,
The Higgs field gives rise to an interaction similar to a weak nuclear interaction in that it has a very small exposure distance and that it becomes ineffective at distances greater than ℏ c / M h ~ 2 × 10 -18 m (1/500 proton radius ), where M h ≈ 125 GeV / c 2 , is the mass of the Higgs particle. At first glance, the formula is similar to the formula for gravity, since the attractive force is proportional to the masses of two elementary particles.
Where v = 246 GeV, this is the constant value of the Higgs field that exists in the entire Universe. (Actually, strictly speaking, there is another square root of 2 in the formula, but let's simplify to improve understanding).
But be careful! The similarity to gravity can be confusing. This formula works for well-known elementary particles - objects that receive their mass from the Higgs field. It works for electrons, muons and quarks. It does not work for protons, neutrons, atoms or you! Because the mass of the proton (and neutron, and therefore the atom, and therefore yours) is not completely generated by the Higgs field. This is different from the formula for gravity, which is true for all slow objects! Instead, in the case of ordinary atomic matter, we would need to replace the formula with a similar one, but with a different factor in front, its own for each atom. But qualitatively, the dependence on the distance would remain similar.
In addition, the formula I wrote assumes the existence of only one Higgs field and one Higgs particle (which has not yet been proved, but is the simplest possibility corresponding to the data obtained). If this is not so, the formula will become more complicated, although it will retain a similar form.

Fig. 2
How strong is this interaction? At very short distances, shorter than 2 × 10 -18m, the Higgs interaction for two quarks is comparable to the strong nuclear interaction at the same distance (see Fig. 2)! But in the case of electrons with a lower mass due to less interaction with the Higgs field, this interaction even at shorter distances will be much weaker than electric ones - more than a thousand million times weaker - although thousands of million million times stronger than the gravitational interaction of electrons . However, if we take two electrons in an atom that are ten million times farther apart from each other than 2 × 10 -18 m, then the Higgs interaction between them will be much, much smaller than even a tiny gravitational interaction, in e 10 000 000time. And even if the Higgs field were responsible for the entire mass of protons and neutrons, then the Higgs interaction in the nucleus would still be much weaker than gravity, which, in turn, is incredibly small compared to the strong nuclear interaction that holds parts of the nucleus.
It is the amazing weakness of the Higgs interaction in the context of ordinary matter that makes it so difficult to detect. On the other hand, the Higgs interaction, like gravity, always works on gravity, and is not balanced. But on the third hand, this does not matter, since, like the weak nuclear interaction, the Higgs interaction does not survive at long distances, since the Higgs particle, like the W particle, has mass. The interaction of Higgs at ultrashort distances is much stronger than gravity, but at nuclear and atomic distances it is much weaker due to the mass of the Higgs particle. And for the small particles of which we are composed, weakly interacting with the Higgs field, the Higgs interaction is always thousands of millions of times weaker than electric forces, even very small distances.
So, although every atom of the Earth interacts via Higgs with every other atom of the Earth, this force is so tiny, even for neighboring atoms, and especially for far-distant ones, that its effect cannot be detected. Therefore, we had to directly find the Higgs particle to confirm the existence of the Higgs field; we could not look for the force created by him in such a way as we can observe electric or magnetic forces and confirm in this way the existence of electric and magnetic fields.
When can we observe the effect of this force? Its effect will be detected for the first time either in the scattering of W and Z particles with each other (which sooner or later will be done, not directly, in proton collisions in the Large Hadron Collider) or in the interactions of the upper quark and the upper antiquark (which can be observed on the electron-positron collider - by the way, I wrote my first work on particle physics about this phenomenon).
