Application of convolutional neural networks for NLP tasks
When we hear about convolutional neural networks (CNNs), we usually think about computer vision. CNN formed the basis for breakthroughs in image classification - the famous AlexNet, winner of the ImageNet competition in 2012, which began a boom in interest in this topic. Since then, convolutional networks have achieved great success in recognizing images, due to the fact that they are arranged like the visual cortex of the brain - that is, they can concentrate on a small area and highlight important features in it. But, as it turned out, CNNs are good not only for this, but also for Natural Language Processing (NLP) tasks. Moreover, in a recent article [1] from a team of authors from Intel and Carnegie-Mellon University, they claim that they are even better for this than RNN,
First, a little theory. What is a convolution? We will not dwell on this in detail, since a ton of materials have already been written about it, but it's still worth a brief run. There is a beautiful visualization from Stanford, which allows you to grasp the essence:
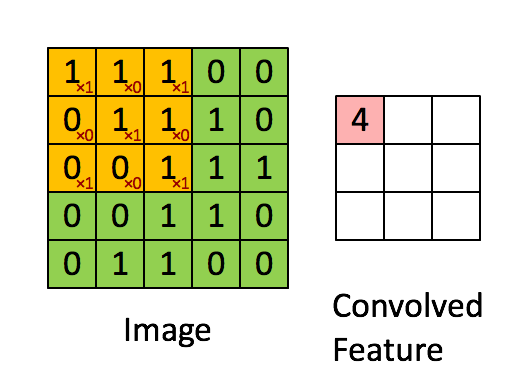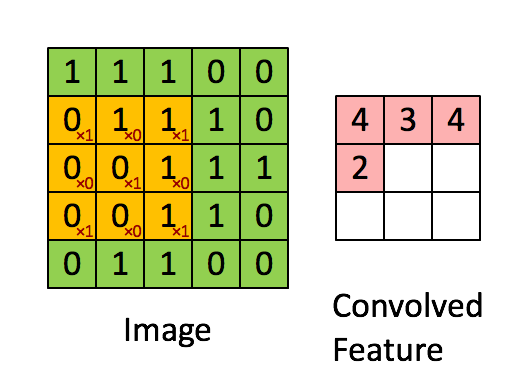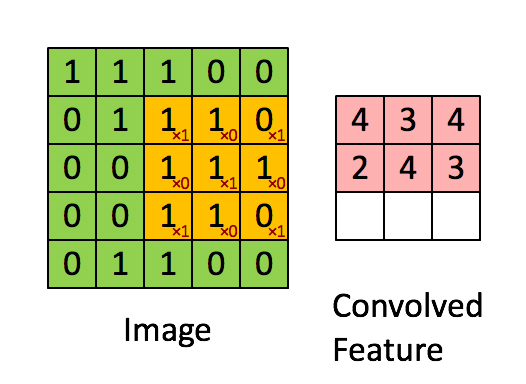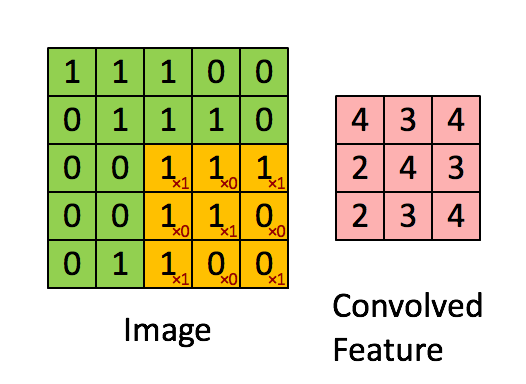
Source
It is necessary to introduce basic concepts, so that later we understand each other. The window that goes around the large matrix is called a filter (in the English version of kernel, filter or feature detector, so you can find translations and tracing of these terms, do not be scared, it's all the same thing). The filter is superimposed on the section of the large matrix and each value is multiplied with the corresponding filter value (red numbers below and to the right of black numbers of the main matrix). Then everything turned out is added up and the output (“filtered”) value is obtained.
The window moves along a large matrix with some step, which in English is called stride. This step can be horizontal and vertical (although the latter is not useful to us).
It remains to introduce an important channel concept. The channels in the images are called basic colors known to many, for example, if we are talking about a simple and widespread RGB color coding scheme (Red - red, Green - green, Blue - blue), then it is assumed that of these three basic colors, by mixing them we can get any color. The key word here is “mixing,” all three basic colors exist simultaneously, and can be obtained from, for example, the white light of the sun using a filter of the desired color (do you feel the terminology is starting to make sense?).
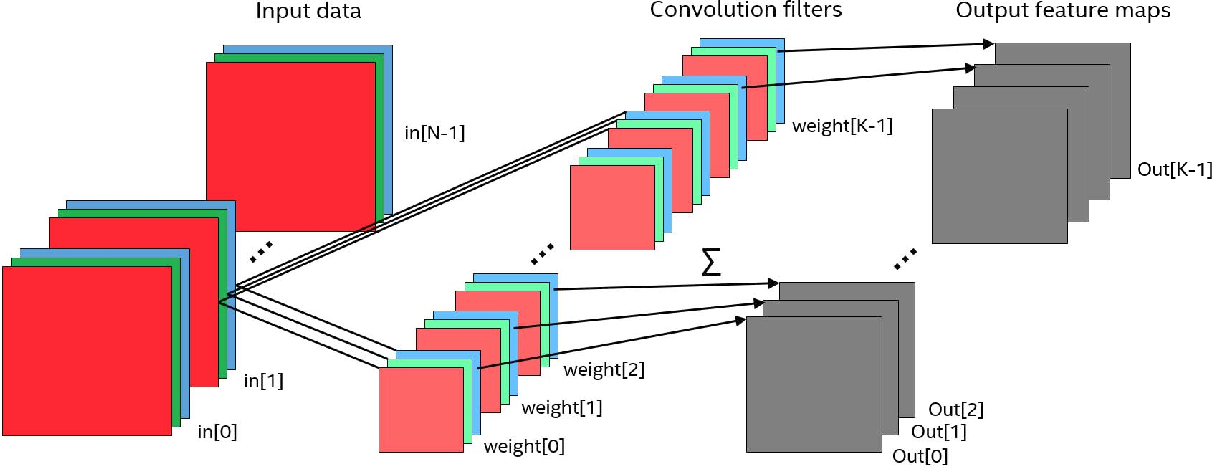
And so it turns out that we have an image, it has channels in it and our filter goes through it with the right step. It remains to understand - what actually to do with these channels? With these channels, we do the following: each filter (that is, a small matrix) is superimposed on the original matrix simultaneously on all three channels. The results are simply summed up (which is logical, if you look, in the end the channels are our way of working with a continuous physical spectrum of light).
It is necessary to mention one more detail, without which further understanding will be difficult: I will tell you a terrible secret, there are much more filters in convolution networks. What does much more mean? This means that we have n filters that do the same job. They walk around the matrix with a window and consider something. It would seem, why do one job twice? One and not one - because of the different initialization of the filtering matrices, in the learning process, they begin to pay attention to different details. For example, one filter looks at the lines, and the other looks at a specific color.

Source: cs231n
This is a visualization of different filters of one layer of one network. See how they look at completely different image features?
Everything, we are armed with terminology in order to move on. In parallel with the terminology, we figured out how the convolutional layer works. It is the basis for convolutional neural networks. There is another base layer for CNN - this is the so-called pooling layer.
The easiest way to explain it is max-pooling. So, imagine that in the convolutional layer already known to you, the filter matrix is fixed and is single (that is, multiplying by it does not affect the input data). And instead of summing up all the multiplication results (input data according to our condition), we simply select the maximum element. That is, we will choose the pixel with the highest intensity from the entire window. This is max-pooling. Of course, instead of functions, the maximum may be another arithmetic (or even more complex) function.
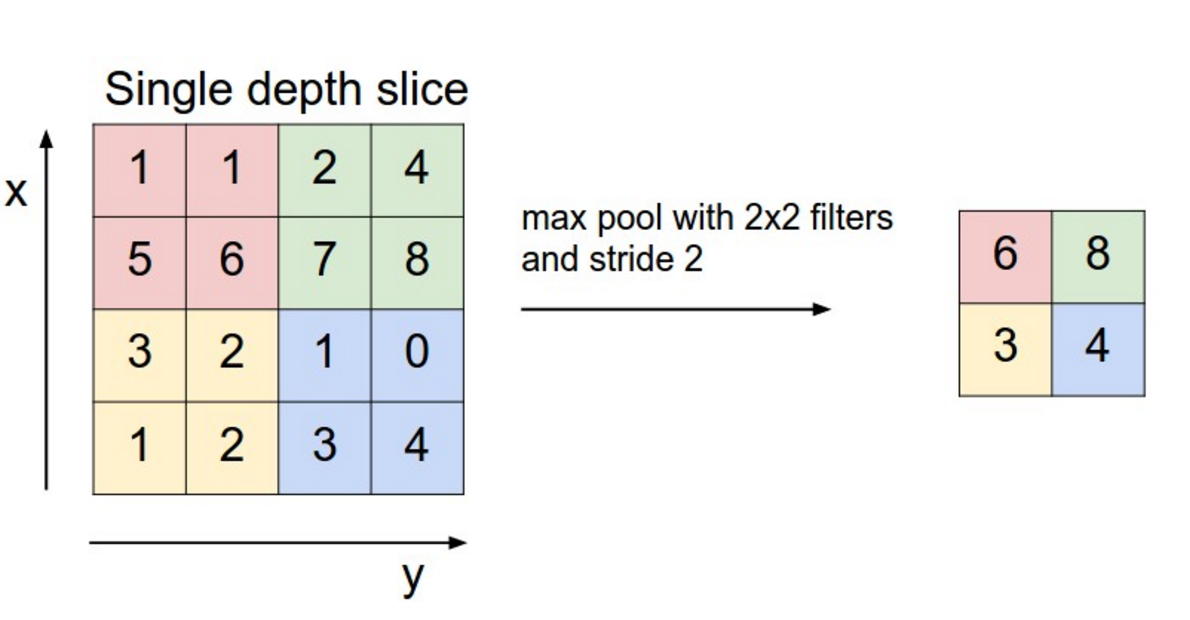
Source: cs231n
For further reading on this subject, I recommend Chris Olah's post .
All of the above is good, but without non-linearity, neural networks will not have the properties of a universal approximator so necessary for us. Accordingly, I must say a few words about them. In recurrent and fully connected networks, nonlinearities such as sigmoid and hyperbolic tangent rule the ball.
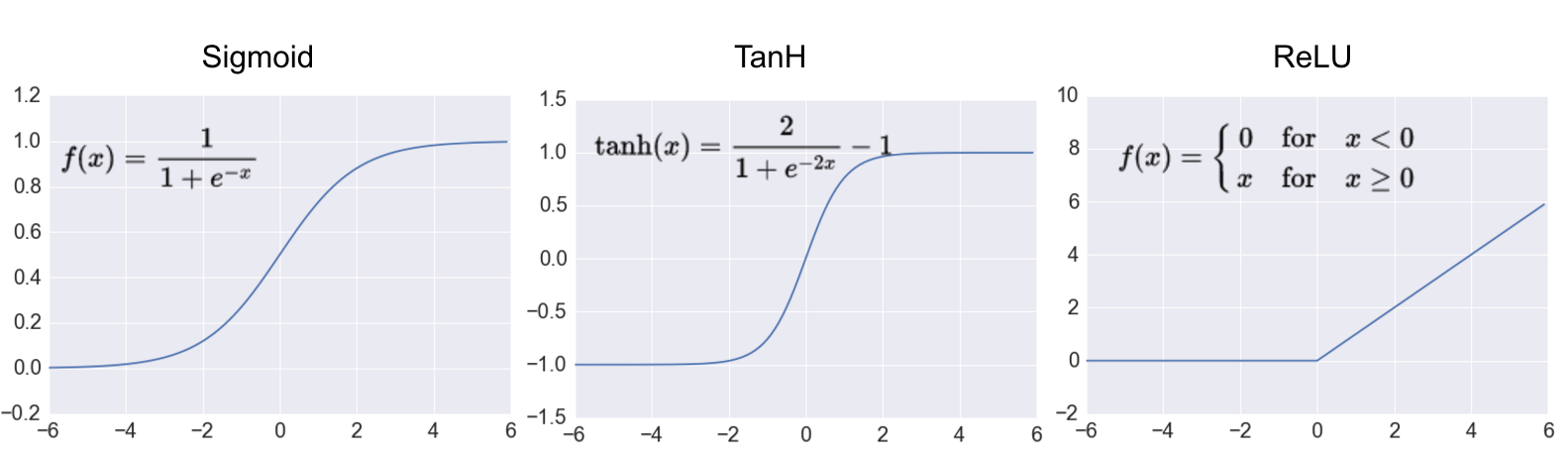
A source
These are good non-linear smooth functions, but they still require significant calculations compared to the one that ruled the ball in CNN: ReLU - Rectified Linear Unit. In Russian, ReLU is usually called a linear filter (are you still not tired of using the word filter?). This is the simplest nonlinear function, besides not smooth. But then it is calculated in one elementary operation, for which developers of computational frameworks are very fond of it.
Well, you and I have already discussed convolutional neural networks, how vision works and all that. But where about the lyrics, or did I shamelessly deceive you? No, I didn’t deceive you.

This picture almost completely explains how we work with text using CNN. Unclear? Let's get it right. First of all, the question is: where do we get the matrix to work from? CNNs work with matrices, right? Here we need to go back a bit and remember what embedding is (there is a separate article about this ).
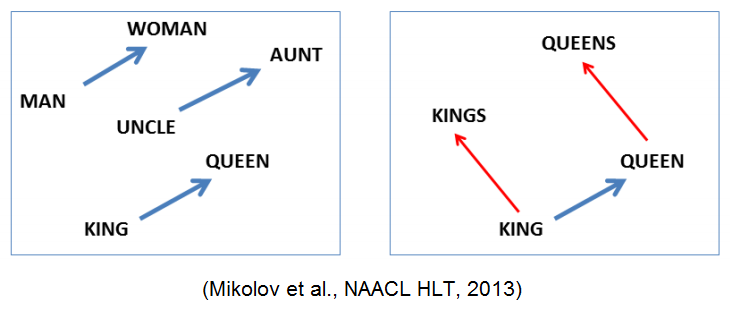
In short, embedding is a mapping of a point in some multidimensional space to an object, in our case, to a word. An example, perhaps the best known of such embedding, is Word2Vec. By the way, it has semantic properties, sort of
Now the next step, the matrix is good, and it seems to even look like a picture - the same two dimensions. Or not? Wait, we have more channels in the picture. It turns out that in the image matrix we have three dimensions - width, height and channels. And here? And here we have only the width (in the title picture of the section, the matrix is transposed for display convenience) - this is a sequence of tokens in the sentence. And - no, not the height, but the channels. Why channels? Because embedding words makes sense only in full, each individual dimension will not tell us anything.
Well, we figured out the matrix, now further about the convolution. It turns out that the convolution we can go only along one axis - in width. Therefore, in order to distinguish from standard convolution, it is called one-dimensional (1D convolution).
And now almost everything is clear, except for the mysterious Max Over Time Pooling. What kind of beast is this? This is the max-pooling already discussed above, only applied to the entire sequence at once (that is, the width of its window is equal to the entire width of the matrix).

A picture to attract attention. Actually an illustration from [4].
Convolutional neural networks are good where you need to see a piece or the entire sequence and make some conclusion from this. That is, these are tasks, for example, detecting spam, analyzing tonality, or extracting named entities. Parsing articles can be difficult for you, if you just got acquainted with neural networks, you can skip this section.
In [2], Yoon Kim shows that CNNs are good for classifying offers on different datasets. The picture used to illustrate the section above is just from his work. It works with Word2Vec, but you can also work directly with characters.
In [3], the authors classify texts based directly on letters, learning embedding for them in the learning process. On large datasets, they showed even better results than networks that worked with words.
Convolutional neural networks have a significant drawback compared to RNNs - they can only work with a fixed-size input (since the size of the matrices in the network cannot change during operation). But the authors of the above work [1] were able to solve this problem. So now this restriction has been removed.
In [4], authors classify texts based directly on characters. They used a set of 70 characters to represent each character as a one-hot vector and set a fixed text length of 1014 characters. Thus, the text is represented by a binary matrix of size 70x1014. The network has no idea about words and sees them as combinations of characters, and information about the semantic proximity of words is not provided to the network, as in the cases of pre-trained Word2Vec vectors. The network consists of 1d conv, max-pooling layers and two fully-connected dropout layers. On large datasets, they showed even better results than networks that worked with words. In addition, this approach significantly simplifies the preprocessing step, which may contribute to its use on mobile devices.
In another work [5], the authors try to improve the application of CNN in NLP using the best practices from computer vision. The main trends in computer vision in recent years is to increase the depth of the network and the addition of the so-called skip-links (eg, ResNet) that connect layers that are not adjacent to each other. The authors showed that the same principles apply to NLP, they built CNN based on characters with 16-dimensional embedding, which they studied with the network. They trained networks of different depths (9, 17, 29 and 49 conv layers) and experimented with skip-links to find out how they affect the result. They concluded that increasing network depth improves results on selected datasets, but the performance of networks that are too deep (49 layers) is lower than moderately deep (29 layers).
Another important feature of CNN in computer vision is the ability to use network weights trained on one large dataset (a typical example is ImageNet) in other computer vision tasks. In [6], the authors examine the applicability of these principles in the task of classifying texts using CNN with word embedding. They study how the transfer of certain parts of the network (Embedding, conv layers and fully-connected layers) affects the classification results on selected datasets. They conclude that in NLP tasks, the semantic proximity of the source on which the network was pre-trained plays an important role, that is, the network trained on movie reviews will work well on a different movie review dataset. In addition, they note that using the same embedding for words increases the success of the transfer and recommend not to freeze the layers,
Let's see in practice how to do sentiment analysis on CNN. We looked at a similar example in an article about Keras , so for all the details I send you to it, and here we will consider only key features to understand.
First of all, you will need the Kequ Sequence concept. Actually, this is the sequence in the form convenient for Keras:
Here
Next, the resulting sequences need to be aligned - as we recall, CNNs do not yet know how to work with variable text lengths, this has not yet reached industrial use.
After that, all sequences will either be trimmed or padded with zeros to length
And now, actually the most important, the code of our model:
The first layer we have is
After embedding is a one-dimensional convolutional layer
After ReLU comes a layer
Here's what model we got in the end:

In the picture, you can notice an interesting feature: after the convolutional layer, the sequence length became 38 instead of 40. Why is this? Because we did not talk and did not use padding, a technique that allows you to virtually “add” data to the original matrix so that Sveta can go beyond it. And without this, a convolution of length 3 with a step equal to 1 can make only 38 steps along a matrix 40 in width.
Okay, what did we get as a result? In my tests, this classifier gave a quality of 0.57, which, of course, is not much. But you can easily improve my result if you make a little effort. Go ahead .
PS: Thank you for your help in writing this article to Evgeny Vasiliev somesnm and Bulat Suleymanov khansuleyman .
[1] Bai, S., Kolter, JZ, & Koltun, V. (2018). An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arxiv.org/abs/1803.01271
[2] Kim, Y. (2014). Convolutional Neural Networks for Sentence Classification. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP 2014), 1746–1751.
[3] Heigold, G., Neumann, G., & van Genabith, J. (2016). Neural morphological tagging from characters for morphologically rich languages. arxiv.org/abs/1606.06640
[4] Character-level Convolutional Networks for Text Classification. Xiang Zhang, Junbo Zhao, Yann LeCun arxiv.org/abs/1509.01626
[5] Very Deep Convolutional Networks for Text Classification. A Conneau, H Schwenk, L Barrault, Y Lecun arxiv.org/abs/1606.01781
[6] A Practitioners' Guide to Transfer Learning for Text Classification using Convolutional Neural Networks. T Semwal, G Mathur, P Yenigalla, SB Nair arxiv.org/abs/1801.06480
Convolutional Neural Networks
First, a little theory. What is a convolution? We will not dwell on this in detail, since a ton of materials have already been written about it, but it's still worth a brief run. There is a beautiful visualization from Stanford, which allows you to grasp the essence:

Source
It is necessary to introduce basic concepts, so that later we understand each other. The window that goes around the large matrix is called a filter (in the English version of kernel, filter or feature detector, so you can find translations and tracing of these terms, do not be scared, it's all the same thing). The filter is superimposed on the section of the large matrix and each value is multiplied with the corresponding filter value (red numbers below and to the right of black numbers of the main matrix). Then everything turned out is added up and the output (“filtered”) value is obtained.
The window moves along a large matrix with some step, which in English is called stride. This step can be horizontal and vertical (although the latter is not useful to us).
It remains to introduce an important channel concept. The channels in the images are called basic colors known to many, for example, if we are talking about a simple and widespread RGB color coding scheme (Red - red, Green - green, Blue - blue), then it is assumed that of these three basic colors, by mixing them we can get any color. The key word here is “mixing,” all three basic colors exist simultaneously, and can be obtained from, for example, the white light of the sun using a filter of the desired color (do you feel the terminology is starting to make sense?).

And so it turns out that we have an image, it has channels in it and our filter goes through it with the right step. It remains to understand - what actually to do with these channels? With these channels, we do the following: each filter (that is, a small matrix) is superimposed on the original matrix simultaneously on all three channels. The results are simply summed up (which is logical, if you look, in the end the channels are our way of working with a continuous physical spectrum of light).
It is necessary to mention one more detail, without which further understanding will be difficult: I will tell you a terrible secret, there are much more filters in convolution networks. What does much more mean? This means that we have n filters that do the same job. They walk around the matrix with a window and consider something. It would seem, why do one job twice? One and not one - because of the different initialization of the filtering matrices, in the learning process, they begin to pay attention to different details. For example, one filter looks at the lines, and the other looks at a specific color.

Source: cs231n
This is a visualization of different filters of one layer of one network. See how they look at completely different image features?
Everything, we are armed with terminology in order to move on. In parallel with the terminology, we figured out how the convolutional layer works. It is the basis for convolutional neural networks. There is another base layer for CNN - this is the so-called pooling layer.
The easiest way to explain it is max-pooling. So, imagine that in the convolutional layer already known to you, the filter matrix is fixed and is single (that is, multiplying by it does not affect the input data). And instead of summing up all the multiplication results (input data according to our condition), we simply select the maximum element. That is, we will choose the pixel with the highest intensity from the entire window. This is max-pooling. Of course, instead of functions, the maximum may be another arithmetic (or even more complex) function.

Source: cs231n
For further reading on this subject, I recommend Chris Olah's post .
All of the above is good, but without non-linearity, neural networks will not have the properties of a universal approximator so necessary for us. Accordingly, I must say a few words about them. In recurrent and fully connected networks, nonlinearities such as sigmoid and hyperbolic tangent rule the ball.

A source
These are good non-linear smooth functions, but they still require significant calculations compared to the one that ruled the ball in CNN: ReLU - Rectified Linear Unit. In Russian, ReLU is usually called a linear filter (are you still not tired of using the word filter?). This is the simplest nonlinear function, besides not smooth. But then it is calculated in one elementary operation, for which developers of computational frameworks are very fond of it.
Well, you and I have already discussed convolutional neural networks, how vision works and all that. But where about the lyrics, or did I shamelessly deceive you? No, I didn’t deceive you.
Applying convolution to texts

This picture almost completely explains how we work with text using CNN. Unclear? Let's get it right. First of all, the question is: where do we get the matrix to work from? CNNs work with matrices, right? Here we need to go back a bit and remember what embedding is (there is a separate article about this ).
In short, embedding is a mapping of a point in some multidimensional space to an object, in our case, to a word. An example, perhaps the best known of such embedding, is Word2Vec. By the way, it has semantic properties, sort of
word2vec(“king”) - word2vec(“man”) + word2vec(“woman”) ~= word2vec(“queen”). So, we take embedding for each word in our text and just put all the vectors in a row, getting the desired matrix.
Now the next step, the matrix is good, and it seems to even look like a picture - the same two dimensions. Or not? Wait, we have more channels in the picture. It turns out that in the image matrix we have three dimensions - width, height and channels. And here? And here we have only the width (in the title picture of the section, the matrix is transposed for display convenience) - this is a sequence of tokens in the sentence. And - no, not the height, but the channels. Why channels? Because embedding words makes sense only in full, each individual dimension will not tell us anything.
Well, we figured out the matrix, now further about the convolution. It turns out that the convolution we can go only along one axis - in width. Therefore, in order to distinguish from standard convolution, it is called one-dimensional (1D convolution).
And now almost everything is clear, except for the mysterious Max Over Time Pooling. What kind of beast is this? This is the max-pooling already discussed above, only applied to the entire sequence at once (that is, the width of its window is equal to the entire width of the matrix).
Examples of the use of convolutional neural networks for texts

Convolutional neural networks are good where you need to see a piece or the entire sequence and make some conclusion from this. That is, these are tasks, for example, detecting spam, analyzing tonality, or extracting named entities. Parsing articles can be difficult for you, if you just got acquainted with neural networks, you can skip this section.
In [2], Yoon Kim shows that CNNs are good for classifying offers on different datasets. The picture used to illustrate the section above is just from his work. It works with Word2Vec, but you can also work directly with characters.
In [3], the authors classify texts based directly on letters, learning embedding for them in the learning process. On large datasets, they showed even better results than networks that worked with words.
Convolutional neural networks have a significant drawback compared to RNNs - they can only work with a fixed-size input (since the size of the matrices in the network cannot change during operation). But the authors of the above work [1] were able to solve this problem. So now this restriction has been removed.
In [4], authors classify texts based directly on characters. They used a set of 70 characters to represent each character as a one-hot vector and set a fixed text length of 1014 characters. Thus, the text is represented by a binary matrix of size 70x1014. The network has no idea about words and sees them as combinations of characters, and information about the semantic proximity of words is not provided to the network, as in the cases of pre-trained Word2Vec vectors. The network consists of 1d conv, max-pooling layers and two fully-connected dropout layers. On large datasets, they showed even better results than networks that worked with words. In addition, this approach significantly simplifies the preprocessing step, which may contribute to its use on mobile devices.
In another work [5], the authors try to improve the application of CNN in NLP using the best practices from computer vision. The main trends in computer vision in recent years is to increase the depth of the network and the addition of the so-called skip-links (eg, ResNet) that connect layers that are not adjacent to each other. The authors showed that the same principles apply to NLP, they built CNN based on characters with 16-dimensional embedding, which they studied with the network. They trained networks of different depths (9, 17, 29 and 49 conv layers) and experimented with skip-links to find out how they affect the result. They concluded that increasing network depth improves results on selected datasets, but the performance of networks that are too deep (49 layers) is lower than moderately deep (29 layers).
Another important feature of CNN in computer vision is the ability to use network weights trained on one large dataset (a typical example is ImageNet) in other computer vision tasks. In [6], the authors examine the applicability of these principles in the task of classifying texts using CNN with word embedding. They study how the transfer of certain parts of the network (Embedding, conv layers and fully-connected layers) affects the classification results on selected datasets. They conclude that in NLP tasks, the semantic proximity of the source on which the network was pre-trained plays an important role, that is, the network trained on movie reviews will work well on a different movie review dataset. In addition, they note that using the same embedding for words increases the success of the transfer and recommend not to freeze the layers,
Practical example
Let's see in practice how to do sentiment analysis on CNN. We looked at a similar example in an article about Keras , so for all the details I send you to it, and here we will consider only key features to understand.
First of all, you will need the Kequ Sequence concept. Actually, this is the sequence in the form convenient for Keras:
x_train = tokenizer.texts_to_sequences(df_train["text"])
x_test = tokenizer.texts_to_sequences(df_test["text"])
x_val = tokenizer.texts_to_sequences(df_val["text"])Here
text_to_sequencesis a function that translates the text into a sequence of integers by a) tokenization, that is, splitting the string into tokens and b) replacing each token with its number in the dictionary. (The dictionary in this example is pre-compiled. The code for compiling it in a full laptop.) Next, the resulting sequences need to be aligned - as we recall, CNNs do not yet know how to work with variable text lengths, this has not yet reached industrial use.
x_train = pad_sequences(x_train, maxlen=max_len)
x_test = pad_sequences(x_test, maxlen=max_len)
x_val = pad_sequences(x_val, maxlen=max_len)After that, all sequences will either be trimmed or padded with zeros to length
max_len. And now, actually the most important, the code of our model:
model = Sequential()
model.add(Embedding(input_dim=max_words, output_dim=128, input_length=max_len))
model.add(Conv1D(128, 3))
model.add(Activation("relu"))
model.add(GlobalMaxPool1D())
model.add(Dense(num_classes))
model.add(Activation('softmax'))The first layer we have is
Embeddingthat translates integers (in fact, one-hot vectors in which the place of the unit corresponds to the number of the word in the dictionary) into dense vectors. In our example, the size of the embedding space (vector length) is 128, the number of words in the dictionary max_words, and the number of words in the sequence are max_len, as we already know from the code above. After embedding is a one-dimensional convolutional layer
Conv1D. The number of filters in it is 128, and the width of the window for filters is 3. Activation should be clear - this is ReLU's favorite. After ReLU comes a layer
GlobalMaxPool1D. “Global” in this case means that it is taken along the entire length of the incoming sequence, that is, it is nothing like the aforementioned Max Over Time Pooling. By the way, why is it called Over Time? Because the sequence of words we have has a natural order, some words come to us earlier in the flow of speech / text, that is, earlier in time. Here's what model we got in the end:

In the picture, you can notice an interesting feature: after the convolutional layer, the sequence length became 38 instead of 40. Why is this? Because we did not talk and did not use padding, a technique that allows you to virtually “add” data to the original matrix so that Sveta can go beyond it. And without this, a convolution of length 3 with a step equal to 1 can make only 38 steps along a matrix 40 in width.
Okay, what did we get as a result? In my tests, this classifier gave a quality of 0.57, which, of course, is not much. But you can easily improve my result if you make a little effort. Go ahead .
PS: Thank you for your help in writing this article to Evgeny Vasiliev somesnm and Bulat Suleymanov khansuleyman .
Literature
[1] Bai, S., Kolter, JZ, & Koltun, V. (2018). An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arxiv.org/abs/1803.01271
[2] Kim, Y. (2014). Convolutional Neural Networks for Sentence Classification. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP 2014), 1746–1751.
[3] Heigold, G., Neumann, G., & van Genabith, J. (2016). Neural morphological tagging from characters for morphologically rich languages. arxiv.org/abs/1606.06640
[4] Character-level Convolutional Networks for Text Classification. Xiang Zhang, Junbo Zhao, Yann LeCun arxiv.org/abs/1509.01626
[5] Very Deep Convolutional Networks for Text Classification. A Conneau, H Schwenk, L Barrault, Y Lecun arxiv.org/abs/1606.01781
[6] A Practitioners' Guide to Transfer Learning for Text Classification using Convolutional Neural Networks. T Semwal, G Mathur, P Yenigalla, SB Nair arxiv.org/abs/1801.06480
