Introducing Google’s S2 Geo-Library and Case Studies
Hello, Habr!
My name is Marco, I work for Badoo in the Platform team. Not so long ago at GopherCon Russia 2018 I talked about how to work with coordinates. For those who do not like to watch videos (and everyone interested, of course), I publish a text version of my report.
Now most people in the world have a smartphone with constant Internet access. Speaking in numbers, in 2018, almost 5 billion people will have a smartphone , and 60% of them use mobile Internet.
These are huge numbers. It has become easy and easy for companies to get user coordinates. These ease and accessibility have spawned (and continue to spawn) a huge number of services based on coordinates.
We all know companies like Uber , games that have conquered the world, such as Ingress and Pokemon Go . But what is there, in any banking application there is the opportunity to see ATMs or discounts nearby.
We at Badoo also use coordinates very actively to provide our users with the best, relevant and interesting service for them. But what kind of use are we talking about? Let's look at the examples of services that we have.
Badoo is primarily a dating. A place where people get to know each other. One of the important criteria when searching for people is distance. Indeed, in most cases, a girl from Moscow wants to meet a boy who is a couple of kilometers from her or at least lives in Moscow, and not in distant Vladivostok.

Services that select people for you to “play” “Yes / No” or show users around, search for people with the criteria that suit you within a certain radius of you.
In order to answer the questions in which city the user is located, in which country or, more precisely, for example, at which airport or at which university, we use the Geoborder service, which deals with the so-called geofencing .

The easiest way to answer these questions would be to consider the distance from the user to the city center or the university center, but this approach is very inaccurate and depends on a large number of boundary conditions.
Therefore, we have drawn very precise borders of countries, cities, important objects (for example, universities and airports, about which I spoke). These boundaries are set by polygons. Having a set of such boundaries, we can understand whether the user is inside the polygon, or find the closest polygon to it. Accordingly, we can say in which city it is, or find the city nearest to it.

We have a very popular feature called Bumped Into, which in the background is constantly looking for users to intersect in time and space and shows you that with this boy or this girl you regularly visit the same place at the same time or regularly take the same road. This feature is very popular with users, because it is another reason to get acquainted with the topic with which you can start a conversation.
Well, the last example that I will mention is related to caching geo-information. Imagine that you use data from, for example, Booking.com, which provides you with information about the hotels around, but it’s too long to go into Booking.com every time. Your pipe to the Internet is perhaps quite narrow, like a hole in this gopher. Perhaps the service you go to for data takes money for each request, and you want to save a little.

In this case, it would be nice to have a caching layer, which will significantly reduce the number of requests for a slow or expensive service, and will provide a very similar API to the outside. A service that will understand that he already knows about all or most of the hotels in this area, this data is relatively fresh, and, accordingly, you can not go into it with an external service. Such tasks are solved by a service called Geocache.
We have already realized that there are many coordinates, coordinates are important, and on the basis of them you can make a lot of interesting services. So what's next? What, in fact, is the matter? How are coordinates different from any other information received from the user?
And there are two features, I would say.

Firstly, the geo-data is three-dimensional, or rather two-dimensional, since in the general case we are not interested in height. They consist of latitude and longitude, and the search most often occurs simultaneously on both. Imagine a search in an area. Standard indexes in common DBMSs are not optimal for such use.
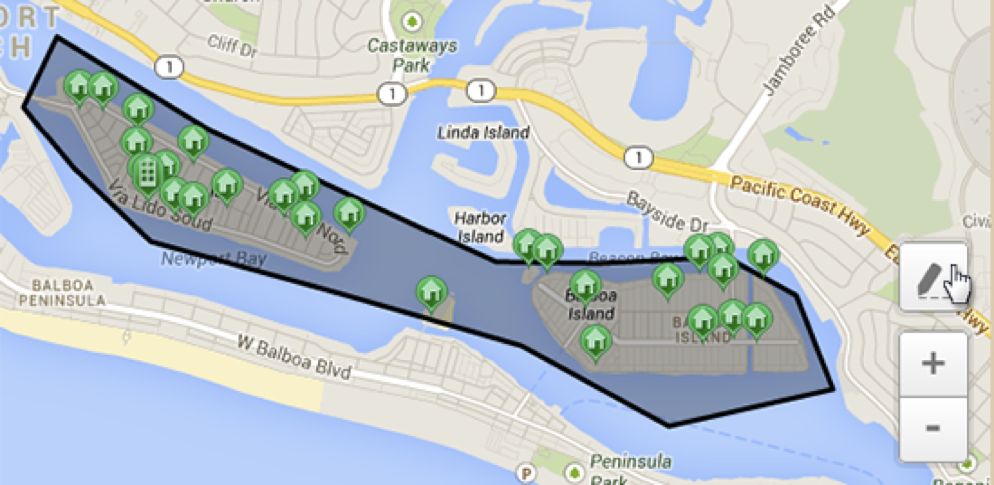
Secondly, many tasks require more complex data types such as polygons, which we talked about above on the example of the Geoborder service in Badoo. Polygons, of course, consist of vertex coordinates, but require additional processing, and search queries on these types of data are also more complicated. We have already seen the queries “Find the nearest polygon to a point” or “Find a polygon that includes a given point”.
In order to comply with these features, many DBMSs include special indexes, sharpened for multidimensional data, and additional functions that allow you to work with objects such as polygons or polylines.

Probably the most striking example is PostGIS - an extension to the popular PostgreSQL DBMS , which has the widest possibilities for working with coordinates and geography.
But using a ready-made DBMS is not the only and not always the best solution.

If you do not want to share the business logic of your service between it and the DBMS, if you want something that is not available in the DBMS, if you want to fully manage your service and not be limited by the ability to scale any DBMS, for example, then you can want to embed the capabilities of searching and working with geo-data in your service.
This approach is undoubtedly more flexible, but it can be much more complicated, because the DBMS is an all-in-one solution, and many infrastructure things like replication have already been done for you. Replication and, in fact, algorithms and indexes for working with coordinates.
But not everything is so scary. I would like to introduce you to a library that implements most of what you need. Which is a kind of cube, easily built-in wherever you need to work with geometry on a sphere or search by coordinates. With a library called S2 .
S2 is a library for working with geometry (including the sphere), which provides very convenient features for creating geo-indexes.
Until recently, S2 was almost unknown and had very poor documentation, but not so long ago Google decided to " re-release " it in open-source, adding to the layout with a promise to support and develop the product.
The main version of the library is written in C ++ and has several official ports or versions in other languages, including the Go version. Today, the Go version does not 100% implement everything that is in the C ++ version, but what it is is enough to implement most things.
In addition to Google, the library is actively used in companies such as Foursquare , Uber ,Yelp , well, and Badoo , of course. And among the products that use the library inside, you can highlight the well-known MongoDB for all of you.
But so far I have not said anything sensible about why S2 is convenient and why it makes it easy to write services with geo-search. Let me correct myself and plunge a little into the insides before we look at two examples.

Typically, geography involves the use of one of the most common projections of the globe on a plane. For example, we all know the Mercator projection . The disadvantage of this approach is that any projection has distortions in one way or another. Our globe is not very similar to a plane.

Remember the famous picture with a comparison of Russia and Africa. Russia is huge on maps, but in fact the area of Africa is already twice as large as the area of Russia! This is just an example of the distortion of the Mercator projection.

S2 solves this problem using exclusively spherical projection and spherical geometry. Of course, the Earth is also not quite a sphere, but distortions in the case of a sphere can be neglected for most tasks.
We will work with a single or unit sphere , that is, with a sphere of radius 1 and we will use concepts such as the central angle , the spherical rectangle, and the spherical segment .
The name S2 comes from the mathematical notation denoting the unit sphere.
But you should not be scared, since almost all the mathematics is taken over by the library.
The second (and most important) feature of the library is the concept of a hierarchical division of the globe into cells (in English - cells).

The division is hierarchical, that is, there is such a thing as the level (or level) of the cell. And at one level, the cells are about the same size.
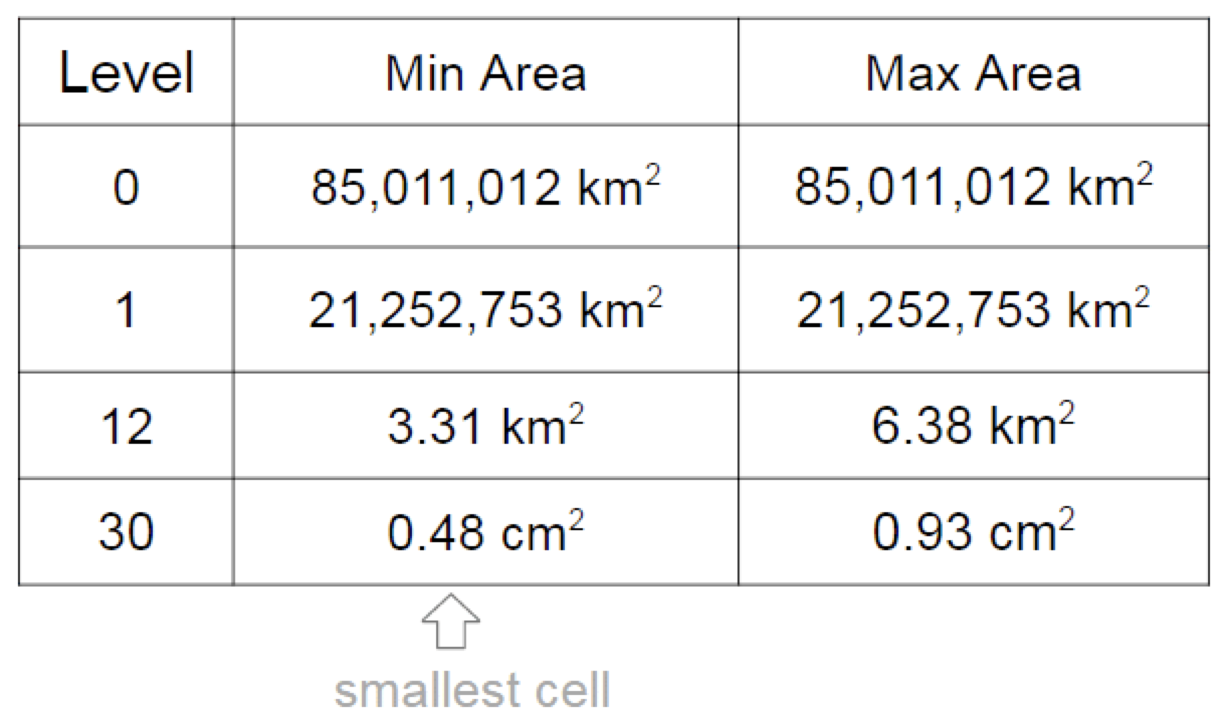
Cells can set any point on Earth. If you use a cell of the maximum, 30th level, which has a size less than a centimeter in width, then the accuracy, as you know, will be very high. The cells of a lower level can set the same point, but the accuracy will already be less. For example, 5 m by 5 m.
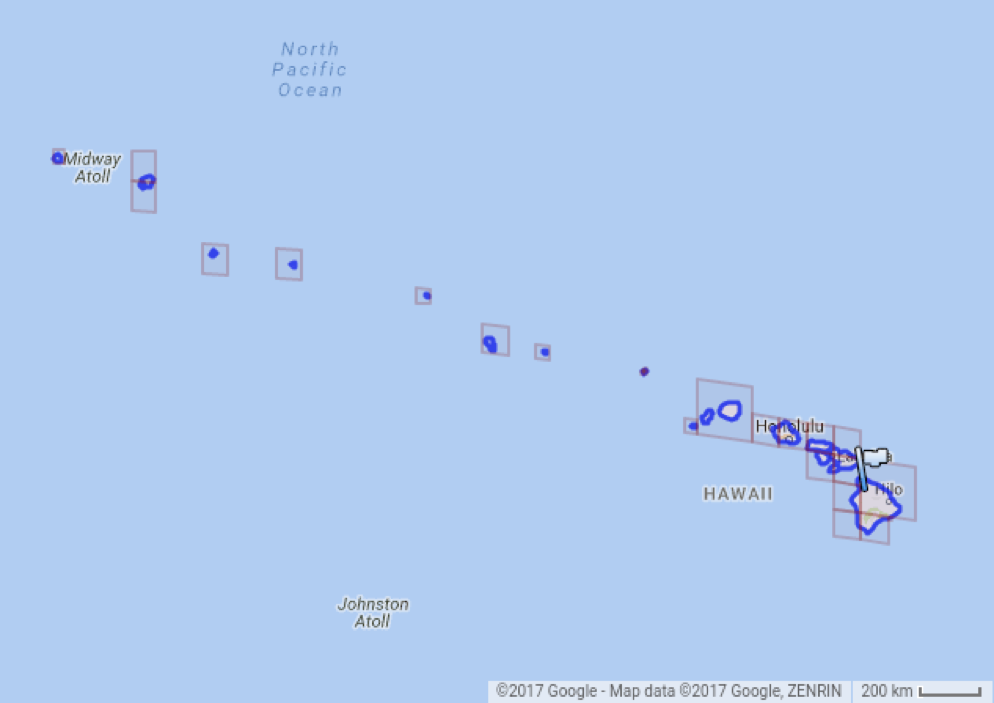
Cells can specify not only points, but also more complex objects such as polygons and some areas (in the picture, for example, you see Hawaii). In this case, such figures will be defined by sets of cells (possibly of different levels).
Such a partition is very compact: each cell can be encoded with one 64-bit number.
I mentioned that a cell is given a single 64-bit number. Here it is! It turns out that the coordinate or point on Earth, which by default is set by two coordinates, with which it is inconvenient for us to work with standard methods, can be given by one number. But how to achieve this? Let's see ...
How does the hierarchical partition of the sphere happen?

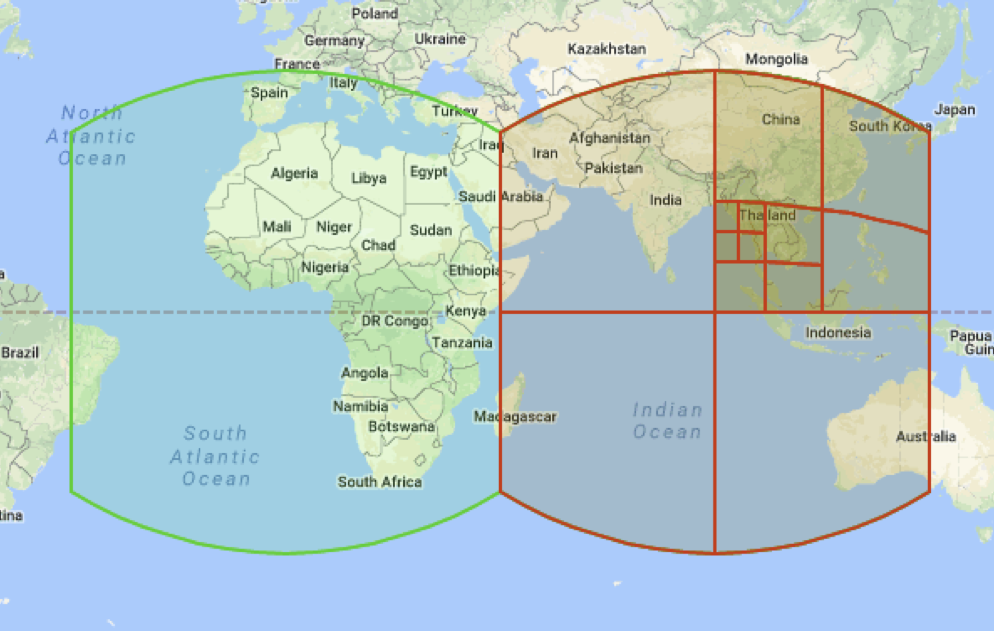
We first surround the sphere with a cube and project it onto all six of its faces, slightly tweaking the projection on the fly to remove distortion. This is level 0. Then we can divide each of the six faces of the cube into four equal parts - this is level 1. And each of the resulting four parts can be divided into four equal parts - level 2. And so on up to level 30.

But at this stage, we still have two-dimensionality. And here, a mathematical idea from the distant past comes to the rescue. At the end of the 19th century, David Hilbert came up with a way to fill any space with a one-dimensional line that rotates, folds and thus fills the space. The Hilbert curve is recursive, which means that precision or density can be chosen. Any small piece we can fill more densely if necessary.

We can fill our two-dimensional space with such a curve. And if now we take this curve and stretch it into a straight line (as if we are pulling a string), then we will get a one-dimensional object that describes a multidimensional object - a one-dimensional object or coordinate on this line, which is convenient and easy to work with.
The filling of the Hilbert curve of the Earth at one of the median levels looks something like this:

Another feature of the Hilbert curve is the fact that the points located nearby on the curve are nearby and in space. The converse is not always, but basically also true. And this feature we will also be actively applying.

But why can we encode any cell with one 64-bit number, which, by the way, is called CellID? Let's get a look.
We have six faces of a cube. Six different values can be encoded in three bits. Remember the logarithms .
Then we break each of the six faces into four equal parts 30 times. To set one of the four parts into which we divide the cell at each level, two bits are enough for us.

Total 3 + 2 * 30 = 63. And we will set one extra bit at the end in order to know and quickly understand what level the cell is given by CellID.

What do all these partitions and coding of the Hilbert curve in one number give us?
Now, to consolidate this theoretical knowledge, let's look at two examples. We will write two simple services, and the first one is just a search around.
We will do a search index. We need a function to create an index, a function to add a person to the index, and, in fact, a search function. Well, the test.
The user is set by their ID and coordinates, and the search by the coordinates of the search center and the radius of the search.
In the index we need a B-tree, in the nodes of which we will store a storageLevel level cell and a list of users in this cell. The storageLevel cell level is the choice between initial search accuracy and performance. In this example, we will use a cell size of approximately 1 km per 1 km. The Less function is necessary for the B-tree to work, so that the tree can understand which of our values is less and which is greater.
Now let's look at the user add function.

Here we first see S2 in action. We convert our coordinates given in degrees to radians, and then to CellID, which corresponds to these coordinates at the maximum 30th level (that is, with the minimum cell size), and convert the resulting CellID to the CellID of the level at which we will keep people. If you look “inside” this function, we will see just zeroing a few bits. Remember how we encoded CellID.
Then we just need to add this user to the appropriate cell in the B-tree. Or first, or at the end of the list, if someone is already there. Our simple index is ready.
Go to the search function. The first transformations are similar, but instead of the cell, we get the point object in coordinates. This is the center of our search.
Further along the radius given in meters, we get the central angle. This is the angle emanating from the center of the sphere. The transformation in this case is simple: it is enough to divide our radius in meters by the radius of the Earth in meters.
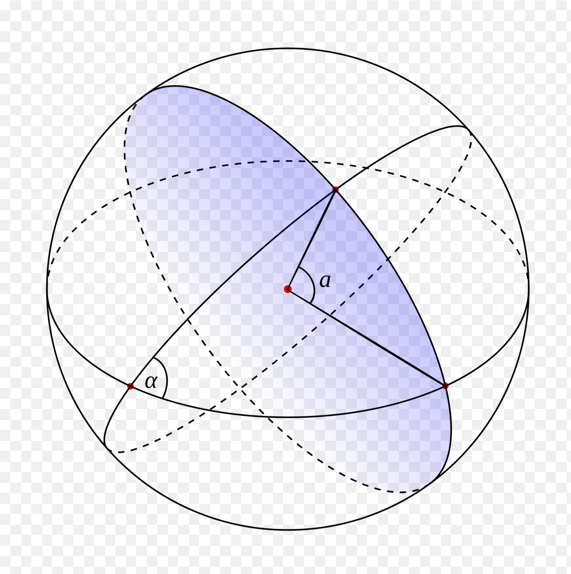
By the point of the search center and by the angle that we just got, we can calculate the spherical segment (or “hat”). In fact, this is a circle on a sphere, but only three-dimensional.
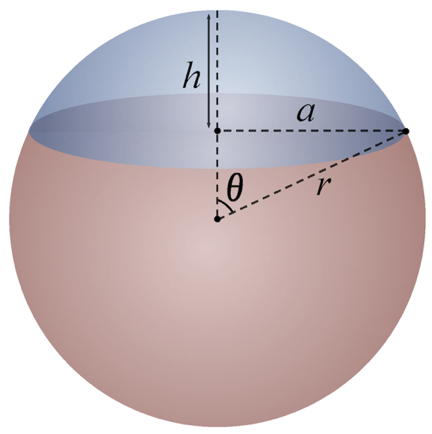
Well, we have a “cap” inside which we need to look. But how? To do this, we ask S2 to give us a list of storageLevel-level cells that completely cover our circle or our “cap”.
It looks something like this:
It remains only to go through the received cells and get-s in the B-tree to get all the users that are inside.
For the test, we will create an index and several users. Three closer, two away. And we’ll check that in the case of a small radius, only three users will return, and in the case of a larger radius, that’s all. Hurrah! Our simple little program works.
But there is one rather obvious flaw in it. In the case of a large search radius and low population density, you will need to check a lot of cells with get-s. This is not so fast.
Recall that we asked S2 to cover our “cap” with storageLevel level cells. But since these cells are quite small, a lot of them turn out.
We can ask S2 to cover the “cap” with cells of different levels; then you get something like this:
As you can see, S2 uses larger cells inside the circle, and smaller ones around the edges. In total, the cells become smaller.
But in order to find users from larger cells in our B-tree, we can no longer use Get. We need to ask S2 for each large cell the number of the first internal cell of our storageLevel level and the number of the last, and look for it already with the help of range scan, that is, the query “from” and “to”.
The change is very minor, but let's look at it in the process. We will write simple benchmarks, which are engaged in a search in a cycle, and run them.
Our small change led to acceleration by three orders of magnitude. Not bad!
We have examined a super-simple implementation of a search by radius. Let's quickly go through the same simple geofencing implementation, that is, determining which polygon we are in or which polygon is closest to us.
Here in our index we similarly need a B-tree, but in addition to it we will have a global map of all added polygons.
In the nodes of the B-tree, as before, we will store the list, but only now the polygons that are in the storageLevel level cell.
In this example, we will have the functions of adding a polygon to the index, searching for the polygon we are in, and finding the nearest polygon.
Let's start by adding a polygon. The polygon is defined by a list of vertices, and S2 expects that the order of the vertices will be counterclockwise. But in case of an error, we will have a function of “normalization”, which, as it were, turns it inside out.
The list of vertex points we will convert to Loop, and then to the polygon. The difference between them is that the polygon can consist of several loops, have a hole, for example, like a donut.
As in the previous example, we will ask S2 to cover our polygon with cells and add each of the returned cells to the B-tree. Well, in the global map.
The polygon search function we are in is trivial in this example. As before, we will transform the search coordinate in CellID at the storageLevel level and find or not find this cell in the B-tree.
Finding the nearest polygon is a bit more complicated. First, we will try to determine if suddenly we are already in some sort of training ground. If not, then we will search by increasing radius (below I will show how it looks). Well, when we find the nearest polygons, we filter them and find the closest one, calculating the distance to each of the found ones and taking the one with the smallest distance.
What does “increasing radius” mean? In the first picture you see an orange cell - the center of our search. First, we will try to find the nearest polygon in all neighboring cells (in the picture they are gray). If we don’t find anything there, then we’ll move one more level, as in the second picture. Etc.


“Neighbors” is given to us by the AllNeighbors function. Unless you need to filter the cells obtained and remove those that we have already viewed.
That, in fact, is all. For this example, I also wrote a test, and it passes successfully.
If you are interested in looking at it or full examples, you can find them here along with the slides.
If you ever need to write a search service that works with coordinates or some more complex geographic features, and you don’t want or cannot use ready-made DBMSs like PostGIS, think about S2.
This is a cool and simple tool that will give you basic things and a framework for working with coordinates and the globe. We at Badoo really love the S2 and strongly recommend it.
Thanks!
Upd: And now the video has arrived!
My name is Marco, I work for Badoo in the Platform team. Not so long ago at GopherCon Russia 2018 I talked about how to work with coordinates. For those who do not like to watch videos (and everyone interested, of course), I publish a text version of my report.

Introduction
Now most people in the world have a smartphone with constant Internet access. Speaking in numbers, in 2018, almost 5 billion people will have a smartphone , and 60% of them use mobile Internet.
These are huge numbers. It has become easy and easy for companies to get user coordinates. These ease and accessibility have spawned (and continue to spawn) a huge number of services based on coordinates.
We all know companies like Uber , games that have conquered the world, such as Ingress and Pokemon Go . But what is there, in any banking application there is the opportunity to see ATMs or discounts nearby.
We at Badoo also use coordinates very actively to provide our users with the best, relevant and interesting service for them. But what kind of use are we talking about? Let's look at the examples of services that we have.
Geo Services at Badoo
First Example: Meetmaker and Geousers
Badoo is primarily a dating. A place where people get to know each other. One of the important criteria when searching for people is distance. Indeed, in most cases, a girl from Moscow wants to meet a boy who is a couple of kilometers from her or at least lives in Moscow, and not in distant Vladivostok.

Services that select people for you to “play” “Yes / No” or show users around, search for people with the criteria that suit you within a certain radius of you.
Second example: Geoborder
In order to answer the questions in which city the user is located, in which country or, more precisely, for example, at which airport or at which university, we use the Geoborder service, which deals with the so-called geofencing .

The easiest way to answer these questions would be to consider the distance from the user to the city center or the university center, but this approach is very inaccurate and depends on a large number of boundary conditions.
Therefore, we have drawn very precise borders of countries, cities, important objects (for example, universities and airports, about which I spoke). These boundaries are set by polygons. Having a set of such boundaries, we can understand whether the user is inside the polygon, or find the closest polygon to it. Accordingly, we can say in which city it is, or find the city nearest to it.
Third Example: Bumpd

We have a very popular feature called Bumped Into, which in the background is constantly looking for users to intersect in time and space and shows you that with this boy or this girl you regularly visit the same place at the same time or regularly take the same road. This feature is very popular with users, because it is another reason to get acquainted with the topic with which you can start a conversation.
Fourth example: Geocache - caching geo-information, which is expensive to "get"
Well, the last example that I will mention is related to caching geo-information. Imagine that you use data from, for example, Booking.com, which provides you with information about the hotels around, but it’s too long to go into Booking.com every time. Your pipe to the Internet is perhaps quite narrow, like a hole in this gopher. Perhaps the service you go to for data takes money for each request, and you want to save a little.

In this case, it would be nice to have a caching layer, which will significantly reduce the number of requests for a slow or expensive service, and will provide a very similar API to the outside. A service that will understand that he already knows about all or most of the hotels in this area, this data is relatively fresh, and, accordingly, you can not go into it with an external service. Such tasks are solved by a service called Geocache.
Features of geo-services
We have already realized that there are many coordinates, coordinates are important, and on the basis of them you can make a lot of interesting services. So what's next? What, in fact, is the matter? How are coordinates different from any other information received from the user?
And there are two features, I would say.

Firstly, the geo-data is three-dimensional, or rather two-dimensional, since in the general case we are not interested in height. They consist of latitude and longitude, and the search most often occurs simultaneously on both. Imagine a search in an area. Standard indexes in common DBMSs are not optimal for such use.

Secondly, many tasks require more complex data types such as polygons, which we talked about above on the example of the Geoborder service in Badoo. Polygons, of course, consist of vertex coordinates, but require additional processing, and search queries on these types of data are also more complicated. We have already seen the queries “Find the nearest polygon to a point” or “Find a polygon that includes a given point”.
Why write your service
In order to comply with these features, many DBMSs include special indexes, sharpened for multidimensional data, and additional functions that allow you to work with objects such as polygons or polylines.

Probably the most striking example is PostGIS - an extension to the popular PostgreSQL DBMS , which has the widest possibilities for working with coordinates and geography.
But using a ready-made DBMS is not the only and not always the best solution.

If you do not want to share the business logic of your service between it and the DBMS, if you want something that is not available in the DBMS, if you want to fully manage your service and not be limited by the ability to scale any DBMS, for example, then you can want to embed the capabilities of searching and working with geo-data in your service.
This approach is undoubtedly more flexible, but it can be much more complicated, because the DBMS is an all-in-one solution, and many infrastructure things like replication have already been done for you. Replication and, in fact, algorithms and indexes for working with coordinates.
But not everything is so scary. I would like to introduce you to a library that implements most of what you need. Which is a kind of cube, easily built-in wherever you need to work with geometry on a sphere or search by coordinates. With a library called S2 .
S2

S2 is a library for working with geometry (including the sphere), which provides very convenient features for creating geo-indexes.
Until recently, S2 was almost unknown and had very poor documentation, but not so long ago Google decided to " re-release " it in open-source, adding to the layout with a promise to support and develop the product.
The main version of the library is written in C ++ and has several official ports or versions in other languages, including the Go version. Today, the Go version does not 100% implement everything that is in the C ++ version, but what it is is enough to implement most things.
In addition to Google, the library is actively used in companies such as Foursquare , Uber ,Yelp , well, and Badoo , of course. And among the products that use the library inside, you can highlight the well-known MongoDB for all of you.
But so far I have not said anything sensible about why S2 is convenient and why it makes it easy to write services with geo-search. Let me correct myself and plunge a little into the insides before we look at two examples.
Projection

Typically, geography involves the use of one of the most common projections of the globe on a plane. For example, we all know the Mercator projection . The disadvantage of this approach is that any projection has distortions in one way or another. Our globe is not very similar to a plane.

Remember the famous picture with a comparison of Russia and Africa. Russia is huge on maps, but in fact the area of Africa is already twice as large as the area of Russia! This is just an example of the distortion of the Mercator projection.

S2 solves this problem using exclusively spherical projection and spherical geometry. Of course, the Earth is also not quite a sphere, but distortions in the case of a sphere can be neglected for most tasks.
We will work with a single or unit sphere , that is, with a sphere of radius 1 and we will use concepts such as the central angle , the spherical rectangle, and the spherical segment .
The name S2 comes from the mathematical notation denoting the unit sphere.
But you should not be scared, since almost all the mathematics is taken over by the library.
Hierarchical cells
The second (and most important) feature of the library is the concept of a hierarchical division of the globe into cells (in English - cells).

The division is hierarchical, that is, there is such a thing as the level (or level) of the cell. And at one level, the cells are about the same size.
Cells can set any point on Earth. If you use a cell of the maximum, 30th level, which has a size less than a centimeter in width, then the accuracy, as you know, will be very high. The cells of a lower level can set the same point, but the accuracy will already be less. For example, 5 m by 5 m.

Cells can specify not only points, but also more complex objects such as polygons and some areas (in the picture, for example, you see Hawaii). In this case, such figures will be defined by sets of cells (possibly of different levels).

Such a partition is very compact: each cell can be encoded with one 64-bit number.
Hilbert curve
I mentioned that a cell is given a single 64-bit number. Here it is! It turns out that the coordinate or point on Earth, which by default is set by two coordinates, with which it is inconvenient for us to work with standard methods, can be given by one number. But how to achieve this? Let's see ...
How does the hierarchical partition of the sphere happen?

We first surround the sphere with a cube and project it onto all six of its faces, slightly tweaking the projection on the fly to remove distortion. This is level 0. Then we can divide each of the six faces of the cube into four equal parts - this is level 1. And each of the resulting four parts can be divided into four equal parts - level 2. And so on up to level 30.

But at this stage, we still have two-dimensionality. And here, a mathematical idea from the distant past comes to the rescue. At the end of the 19th century, David Hilbert came up with a way to fill any space with a one-dimensional line that rotates, folds and thus fills the space. The Hilbert curve is recursive, which means that precision or density can be chosen. Any small piece we can fill more densely if necessary.

We can fill our two-dimensional space with such a curve. And if now we take this curve and stretch it into a straight line (as if we are pulling a string), then we will get a one-dimensional object that describes a multidimensional object - a one-dimensional object or coordinate on this line, which is convenient and easy to work with.
The filling of the Hilbert curve of the Earth at one of the median levels looks something like this:

Another feature of the Hilbert curve is the fact that the points located nearby on the curve are nearby and in space. The converse is not always, but basically also true. And this feature we will also be actively applying.

Encoding into a 64-bit variable
But why can we encode any cell with one 64-bit number, which, by the way, is called CellID? Let's get a look.
We have six faces of a cube. Six different values can be encoded in three bits. Remember the logarithms .
Then we break each of the six faces into four equal parts 30 times. To set one of the four parts into which we divide the cell at each level, two bits are enough for us.

Total 3 + 2 * 30 = 63. And we will set one extra bit at the end in order to know and quickly understand what level the cell is given by CellID.

What do all these partitions and coding of the Hilbert curve in one number give us?
- We can encode any point on the globe with one CellID. Depending on the level, we get different accuracy.
- Any two-dimensional object on the globe, we can encode one or more CellID. Similarly, we can play with precision by varying levels.
- The property of the Hilbert curve that the points that are next to it are near and in space, and the fact that CellID is just a number, allows us to use an ordinary tree of the B-tree type for searching. Depending on what we are looking for (point or region), we will use either get, or range scan, that is, the search “from” and “to”.
- Dividing the globe into levels gives us a simple framework for sharding our system. For example, at the zero level, we can divide our service into six instances, at the first level - at 24, etc.
Now, to consolidate this theoretical knowledge, let's look at two examples. We will write two simple services, and the first one is just a search around.
Examples
We will write a service for finding people around
We will do a search index. We need a function to create an index, a function to add a person to the index, and, in fact, a search function. Well, the test.
type Index struct {}
func NewIndex(storageLevel int) *Index {}
func (i *Index) AddUser(userID uint32, lon, lat float64) error {}
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {}
func TestSearch(t *testing.T) {}
The user is set by their ID and coordinates, and the search by the coordinates of the search center and the radius of the search.
In the index we need a B-tree, in the nodes of which we will store a storageLevel level cell and a list of users in this cell. The storageLevel cell level is the choice between initial search accuracy and performance. In this example, we will use a cell size of approximately 1 km per 1 km. The Less function is necessary for the B-tree to work, so that the tree can understand which of our values is less and which is greater.
type Index struct {
storageLevel int
bt *btree.BTree
}
type userList struct {
cellID s2.CellID
list []uint32
}
func (ul userList) Less(than btree.Item) bool {
return uint64(ul.cellID) < uint64(than.(userList).cellID)
}
Now let's look at the user add function.
func (i *Index) AddUser(userID uint32, lon, lat float64) error {
latlng := s2.LatLngFromDegrees(lat, lon)
cellID := s2.CellIDFromLatLng(latlng)
cellIDOnStorageLevel := cellID.Parent(i.storageLevel)
// ...
}

Here we first see S2 in action. We convert our coordinates given in degrees to radians, and then to CellID, which corresponds to these coordinates at the maximum 30th level (that is, with the minimum cell size), and convert the resulting CellID to the CellID of the level at which we will keep people. If you look “inside” this function, we will see just zeroing a few bits. Remember how we encoded CellID.
func (i *Index) AddUser(userID uint32, lon, lat float64) error {
// ...
ul := userList{cellID: cellIDOnStorageLevel, list: nil}
item := i.bt.Get(ul)
if item != nil {
ul = item.(userList)
}
ul.list = append(ul.list, userID)
i.bt.ReplaceOrInsert(ul)
return nil
}
Then we just need to add this user to the appropriate cell in the B-tree. Or first, or at the end of the list, if someone is already there. Our simple index is ready.
Go to the search function. The first transformations are similar, but instead of the cell, we get the point object in coordinates. This is the center of our search.
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {
latlng := s2.LatLngFromDegrees(lat, lon)
centerPoint := s2.PointFromLatLng(latlng)
centerAngle := float64(radius) / EarthRadiusM
cap := s2.CapFromCenterAngle(centerPoint, s1.Angle(centerAngle))
// ...
return result, nil
}
Further along the radius given in meters, we get the central angle. This is the angle emanating from the center of the sphere. The transformation in this case is simple: it is enough to divide our radius in meters by the radius of the Earth in meters.

By the point of the search center and by the angle that we just got, we can calculate the spherical segment (or “hat”). In fact, this is a circle on a sphere, but only three-dimensional.

Well, we have a “cap” inside which we need to look. But how? To do this, we ask S2 to give us a list of storageLevel-level cells that completely cover our circle or our “cap”.
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {
// ...
rc := s2.RegionCoverer{MaxLevel: i.storageLevel, MinLevel: i.storageLevel}
cu := rc.Covering(cap)
// ...
return result, nil
}
It looks something like this:

It remains only to go through the received cells and get-s in the B-tree to get all the users that are inside.
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {
// ...
var result []uint32
for _, cellID := range cu {
item := i.bt.Get(userList{cellID: cellID})
if item != nil {
result = append(result, item.(userList).list...)
}
}
return result, nil
}
For the test, we will create an index and several users. Three closer, two away. And we’ll check that in the case of a small radius, only three users will return, and in the case of a larger radius, that’s all. Hurrah! Our simple little program works.
func prepare() *Index {
i := NewIndex(13 /* ~ 1km */)
i.AddUser(1, 14.1313, 14.1313)
i.AddUser(2, 14.1314, 14.1314)
i.AddUser(3, 14.1311, 14.1311)
i.AddUser(10, 14.2313, 14.2313)
i.AddUser(11, 14.0313, 14.0313)
return i
}
func TestSearch(t *testing.T) {
indx := prepare()
found, _ := indx.Search(14.1313, 14.1313, 2000)
if len(found) != 3 {
t.Fatal("error while searching with radius 2000")
}
found, _ = indx.Search(14.1313, 14.1313, 20000)
if len(found) != 5 {
t.Fatal("error while searching with radius 20000")
}
}
$ go test -run 'TestSearch$'
PASS
ok github.com/mkevac/gophercon-russia-2018/geosearch 0.008s
But there is one rather obvious flaw in it. In the case of a large search radius and low population density, you will need to check a lot of cells with get-s. This is not so fast.
Recall that we asked S2 to cover our “cap” with storageLevel level cells. But since these cells are quite small, a lot of them turn out.
We can ask S2 to cover the “cap” with cells of different levels; then you get something like this:
rc := s2.RegionCoverer{MaxLevel: i.storageLevel}
cu := rc.Covering(cap)

As you can see, S2 uses larger cells inside the circle, and smaller ones around the edges. In total, the cells become smaller.
But in order to find users from larger cells in our B-tree, we can no longer use Get. We need to ask S2 for each large cell the number of the first internal cell of our storageLevel level and the number of the last, and look for it already with the help of range scan, that is, the query “from” and “to”.
func (i *Index) SearchFaster(lon, lat float64, radius uint32) ([]uint32, error) {
// ...
for _, cellID := range cu {
if cellID.Level() < i.storageLevel
begin := cellID.ChildBeginAtLevel(i.storageLevel)
end := cellID.ChildEndAtLevel(i.storageLevel)
i.bt.AscendRange(userList{cellID: begin}, userList{cellID: end.Next()},func(item btree.Item) bool {
result = append(result, item.(userList).list...)
return true
})
} else {
// ...
}
}
return result, nil
}
The change is very minor, but let's look at it in the process. We will write simple benchmarks, which are engaged in a search in a cycle, and run them.
var res []uint32
func BenchmarkSearch(b *testing.B) {
indx := prepare()
for i := 0; i < b.N; i++ {
res, _ = indx.Search(14.1313, 14.1313, 50000)
}
}
func BenchmarkSearchFaster(b *testing.B) {
indx := prepare()
for i := 0; i < b.N; i++ {
res, _ = indx.SearchFaster(14.1313, 14.1313, 50000)
}
}
Our small change led to acceleration by three orders of magnitude. Not bad!
$ go test -bench=.
goos: darwin
goarch: amd64
pkg: github.com/mkevac/gophercon-russia-2018/geosearch
BenchmarkSearch-8 500 3097564 ns/op
BenchmarkSearchFaster-8 200000 7198 ns/op
PASS
ok github.com/mkevac/gophercon-russia-2018/geosearch 3.393sLet's write a geofencing service
We have examined a super-simple implementation of a search by radius. Let's quickly go through the same simple geofencing implementation, that is, determining which polygon we are in or which polygon is closest to us.
Here in our index we similarly need a B-tree, but in addition to it we will have a global map of all added polygons.
type Index struct {
storageLevel int
bt *btree.BTree
polygons map[uint32]*s2.Polygon
}
func NewIndex(storageLevel int) *Index {
return &Index{
storageLevel: storageLevel,
bt: btree.New(35),
polygons: make(map[uint32]*s2.Polygon),
}
}
In the nodes of the B-tree, as before, we will store the list, but only now the polygons that are in the storageLevel level cell.
type IndexItem struct {
cellID s2.CellID
polygonsInCell []uint32
}
func (ii IndexItem) Less(than btree.Item) bool {
return uint64(ii.cellID) < uint64(than.(IndexItem).cellID)
}
In this example, we will have the functions of adding a polygon to the index, searching for the polygon we are in, and finding the nearest polygon.
func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error {}
func (i *Index) Search(lon, lat float64) ([]uint32, error) {}
func (i *Index) SearchNearest(lon, lat float64) ([]uint32, error) {}
Let's start by adding a polygon. The polygon is defined by a list of vertices, and S2 expects that the order of the vertices will be counterclockwise. But in case of an error, we will have a function of “normalization”, which, as it were, turns it inside out.
func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error {
points := func() (res []s2.Point) {
for _, vertex := range vertices {
point := s2.PointFromLatLng(vertex)
res = append(res, point)
}
return
}()
loop := s2.LoopFromPoints(points)
loop.Normalize()
polygon := s2.PolygonFromLoops([]*s2.Loop{loop})
// ...
return nil
}
The list of vertex points we will convert to Loop, and then to the polygon. The difference between them is that the polygon can consist of several loops, have a hole, for example, like a donut.
As in the previous example, we will ask S2 to cover our polygon with cells and add each of the returned cells to the B-tree. Well, in the global map.
func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error {
// ...
coverer := s2.RegionCoverer{MinLevel: i.storageLevel, MaxLevel: i.storageLevel}
cells := coverer.Covering(polygon)
for _, cell := range cells {
// ...
ii.polygonsInCell = append(ii.polygonsInCell, polygonID)
i.bt.ReplaceOrInsert(ii)
}
i.polygons[polygonID] = polygon
return nil
}
The polygon search function we are in is trivial in this example. As before, we will transform the search coordinate in CellID at the storageLevel level and find or not find this cell in the B-tree.
func (i *Index) Search(lon, lat float64) ([]uint32, error) {
latlng := s2.LatLngFromDegrees(lat, lon)
cellID := s2.CellIDFromLatLng(latlng)
cellIDOnStorageLevel := cellID.Parent(i.storageLevel)
item := i.bt.Get(IndexItem{cellID: cellIDOnStorageLevel})
if item != nil {
return item.(IndexItem).polygonsInCell, nil
}
return []uint32{}, nil
}
Finding the nearest polygon is a bit more complicated. First, we will try to determine if suddenly we are already in some sort of training ground. If not, then we will search by increasing radius (below I will show how it looks). Well, when we find the nearest polygons, we filter them and find the closest one, calculating the distance to each of the found ones and taking the one with the smallest distance.
func (i *Index) SearchNearest(lon, lat float64) ([]uint32, error) {
// ...
alreadyVisited := []s2.CellID{cellID}
var found []IndexItem
searched := []s2.CellID{cellID}
for {
found, searched = i.searchNextLevel(searched, &alreadyVisited)
if len(searched) == 0 {
break
}
if len(found) > 0 {
return i.filter(lon, lat, found), nil
}
}
return []uint32{}, nil
}
What does “increasing radius” mean? In the first picture you see an orange cell - the center of our search. First, we will try to find the nearest polygon in all neighboring cells (in the picture they are gray). If we don’t find anything there, then we’ll move one more level, as in the second picture. Etc.


“Neighbors” is given to us by the AllNeighbors function. Unless you need to filter the cells obtained and remove those that we have already viewed.
func (i *Index) searchNextLevel(radiusEdges []s2.CellID,
alreadyVisited *[]s2.CellID) (found []IndexItem, searched []s2.CellID) {
for _, radiusEdge := range radiusEdges {
neighbors := radiusEdge.AllNeighbors(i.storageLevel)
for _, neighbor := range neighbors {
if in(*alreadyVisited, neighbor) {
continue
}
*alreadyVisited = append(*alreadyVisited, neighbor)
searched = append(searched, neighbor)
item := i.bt.Get(IndexItem{cellID: neighbor})
if item != nil {
found = append(found, item.(IndexItem))
}
}
}
return
}
That, in fact, is all. For this example, I also wrote a test, and it passes successfully.
If you are interested in looking at it or full examples, you can find them here along with the slides.
Conclusion
If you ever need to write a search service that works with coordinates or some more complex geographic features, and you don’t want or cannot use ready-made DBMSs like PostGIS, think about S2.
This is a cool and simple tool that will give you basic things and a framework for working with coordinates and the globe. We at Badoo really love the S2 and strongly recommend it.
Thanks!
Upd: And now the video has arrived!
