The book "Highly loaded applications. Programming, scaling, support "

In this book you will find key principles, algorithms and trade-offs that can not be avoided when developing highly loaded systems for working with data. The material is considered on the example of the internal structure of popular software packages and frameworks. The book has three main parts, devoted primarily to the theoretical aspects of working with distributed systems and databases. The reader is required to have basic knowledge of SQL and how databases work.

The review post covers the section “Knowledge, Truth, and Falsehood.”

If you do not have experience with distributed systems, the consequences of these problems can be very disorienting. The host knows for sure nothing - it can only make assumptions based on the messages it receives (or does not receive) over the network. One node is able to find out the state of another node (what data is stored on it, whether it works correctly) only by exchanging messages with it. If the remote host does not respond, then there is no way to find out its status, since it is impossible to distinguish network problems from problems in the host.


Discussions of these systems border on philosophy: what is true in our system and what is false? Can we rely on this knowledge if the mechanisms of cognition and measurement are unreliable? Should software systems obey the laws of the physical world, such as the law of cause and effect?

Fortunately, we do not need to look for the meaning of life. For a distributed system, you can describe the assumptions about the behavior (system model) and design it so that it matches these assumptions. It is possible to verify the correct operation of the algorithms within the framework of a particular system model. This means that reliability is achievable, even if the underlying model provides very few guarantees.

However, although it is possible to ensure proper operation of the system with an unreliable model, this is not easy. In the remainder of this chapter, we will discuss the concepts of knowledge and truth in distributed systems, which will help us deal with the necessary assumptions and guarantees. In Chapter 9, we move on to consider a number of examples of distributed systems and algorithms that provide specific guarantees with specific assumptions.

Truth is determined by most

Imagine a network with an asymmetric failure: the host receives all messages sent to it, but all its outgoing messages are delayed or even discarded. And although it works fine and receives requests from other nodes, these others do not receive its answers. As a result, after some waiting time, other nodes declare it idle. The situation turns into some kind of nightmare: a node that is half disconnected from the network is forcibly dragged by a “graveyard”, and it fights off and shouts: “I'm alive!”. But since no one hears his screams, the funeral procession steadily continues to move.

In a slightly less nightmare scenario, a node that is half disconnected from the network may notice that there is no confirmation of delivery of its messages from other nodes and understands that there is a network failure. However, other nodes mistakenly declare the half-disconnected node inoperative, and he is not able to do anything about it.

As a third scenario, imagine a node suspended for a long time due to lengthy comprehensive garbage collection. All its threads are forced out of memory by the garbage collection process and are suspended for a minute, and, therefore, requests are not processed, and responses are not sent. Other nodes wait, retry, lose patience, eventually declare the node inoperative and "send it to the hearse." Finally, the garbage collection process exits and the node flows resume as if nothing had happened. The remaining nodes are surprised at the “resurrection” in full health of the node declared “dead” and begin to chat joyfully with eyewitnesses to this. At first, this node does not even understand that a whole minute has passed and it has been declared “dead” - from his point of view, almost a moment has passed from the moment of the last message exchange with other nodes.

The moral of these stories is: the knot cannot rely solely on its own opinion about the situation. A distributed system cannot fully rely on a single node, since it is capable of failing at any time, leading to failure and the inability to restore the system. Instead, many distributed algorithms base their work on a quorum, that is, solving most nodes (see the “Writing and reading quorum operations” section of the “Writing to the database when one of the nodes fails” section 5.4): making decisions requires a certain minimum amount "Votes" from several nodes. This condition allows you to reduce the dependence on any one particular node.

This includes decisions to declare nodes inoperative. If the quorum of nodes declares another node inoperative, then it is considered to be such, even if it works great at the same time. Individual nodes are required to obey quorum decisions.

Typically, a quorum is the absolute majority of more than half the nodes (although there are other varieties of quorums). For the most part, a quorum allows the system to work in the event of failure of individual nodes (for three nodes, a failure of one is acceptable, and for five, a failure of two). This method is safe, because the system can have only one majority - two majority at the same time, whose decisions conflict, are impossible. We will discuss the use of quorums in more detail when we get to the consensus algorithms in chapter 9.

Host and locks

Often, the system needs only one instance of something. For instance:

• only one node can be the leader for the database section in order to avoid the situation of separation of computing power (see the subsection "Interruptions in the maintenance of nodes" in section 5.1);
• only one transaction or one client can hold a lock on a specific resource or object in order to prevent a competitive entry into it and its damage;
• only one user can register a specific username, because it must uniquely identify the user.

Implementation of this in a distributed system requires caution: even if the node is confident in its “chosenness” (the leading node of the section, the owner of the lock, the request handler that has successfully captured the username), it is not at all a fact that the quorum of the other nodes agrees! A node could previously be a leader, but if then other nodes declared it to be inoperative (for example, due to a network break or a pause for garbage collection), then it could well be "demoted" and choose another master node.

The case when the node continues to behave as “chosen”, despite the fact that the quorum of the other nodes declared it inoperative, can lead to problems in an insufficiently carefully designed system. Such a node is able to send messages to other nodes as a self-proclaimed “chosen” one, and if other nodes agree with this, the system as a whole may start to work incorrectly.

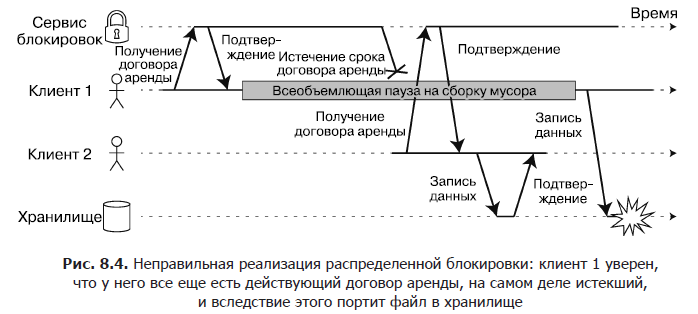
For example, in fig. Figure 8.4 shows an error with data corruption due to improper implementation of locking (this is by no means a theoretical error: it often occurs in the HBase DBMS). Suppose we would like to make sure that only one client can access the file located in the storage service at the same time, because if several clients immediately try to write to it, the file will be corrupted. We will try to implement this with the help of the obligatory receipt by the client of a lease from the lock service before accessing the file.

The described problem is an example of what we discussed in the section “Pauses during the execution of processes” of section 8.3: if the tenant pauses for too long, then his lease agreement expires. After that, another client can receive a lease for the same file and start writing data to it. After resuming work, the suspended client believes (erroneously) that he still has a valid lease, and proceeds to write to the file. As a result, the write operations of the two clients are mixed and the file is corrupted.

Fencing Markers

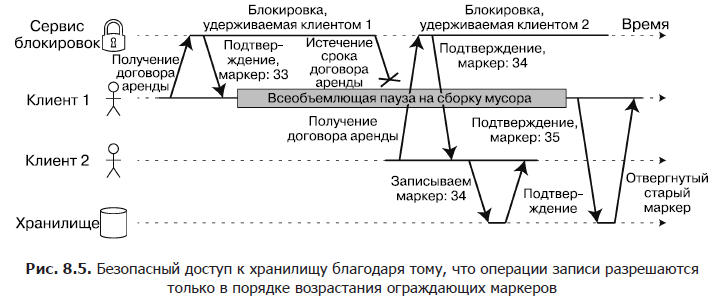
When using a lock or lease to protect access to a resource, such as the file storage in Figure 8.4, you need to make sure that a node that mistakenly considers itself “elected” will not disrupt the operation of the rest of the system. For this purpose, there is a fairly simple method shown in Fig. 8.5. It is called fencing.

Imagine that each time a lock or lease is provided, the lock server also returns a fencing token, which is a number that is incremented each time a lock is provided (for example, the lock service can increase it). In addition, we require that the client each time they send a write request to the storage service include such a marker in the current request.

In fig. 8.5 client 1 receives a lease with marker 33, after which it is suspended for a long time, and the lease expires. Client 2 receives a lease with a marker 34 (the number increases monotonously), and then sends a write request to the storage service, including this token in the request. Later, client 1 resumes operation and sends the write operation with marker 33 to the storage service. However, the storage service remembers that it has already processed the write operation with a large marker number (34) and rejects this request.

When using ZooKeeper locks as a guard token, you can use the transaction identifier zxid or the version of the cversion node. Since ZooKeeper guarantees their monotonous increase, they possess the necessary properties for this.


Please note: this mechanism requires that the resource itself takes an active part in the verification of tokens, rejecting all write operations with tokens older than those already processed - checking the blocking status on the clients themselves is not enough. You can bypass the limitation for resources that do not explicitly support boundary markers (for example, in the case of a file storage service, a boundary marker is included in the file name). However, some verification is still needed to avoid processing requests without blocking protection.

Checking the tokens on the server side may seem like a flaw, but it is probably not so bad: for a service it would be unreasonable to assume that all its clients always “behave well”, since clients are often launched by people with different priorities such as from service owners. Therefore, it would be a good idea for any service to protect itself from unintended improper actions on the part of customers.

Byzantine glitches

Fencing markers are able to detect and block a node that inadvertently performs erroneous actions (for example, because it has not yet detected the expiration of its lease agreement). However, a site intentionally wanting to undermine system guarantees can easily do this by sending a message with a fake marker.

In this book, we assume that the nodes are unreliable but “decent”: they may run slowly or not respond at all (due to a failure), their state may be outdated (due to a pause in garbage collection or network delays), but if the node at all answers, then he “tells the truth” (complies with the rules of the protocol in the framework of the information available to him).

The problems of distributed systems are significantly exacerbated if there is a risk that the nodes can “lie” (send arbitrary failed or damaged responses) - for example, if the node can announce the receipt of a certain message when it really was not. This behavior is called the Byzantine fault, and the task of reaching consensus in such an untrustworthy environment is known as the Byzantine generals problem.

The system is protected from Byzantine failures if it continues to work correctly even in the event of a malfunction of some nodes and their failure to comply with the protocol or when intruders interfere with the network. This may be important in the following circumstances.

• In the aerospace industry, data in computer memory or CPU registers can be corrupted due to radiation, which leads to sending unpredictable responses to other nodes. Since a system failure can lead to catastrophic consequences (for example, a plane crash and the death of everyone on board or a rocket colliding with the International Space Station), flight control systems must be protected from Byzantine glitches.
• Some participants in a system with many participating organizations may try to cheat or trick others. In such circumstances, the site should not blindly trust messages from other sites, as they can be sent with malicious intent. For example, peer-to-peer networks, such as Bitcoin and other blockchains, can be seen as a way for parties not trusting each other to agree whether a transaction has occurred without relying on any central authority.

However, in such systems that we discuss in this book, you can usually safely assume that there are no Byzantine failures. In your data center, all nodes are controlled by your organization (so they are, we hope, trusted), and the radiation levels are low enough so that memory corruption does not present a serious problem. Protocols for creating Byzantine-protected systems failures are quite complex, and such embedded systems require hardware support. In most server information systems, Byzantine-fault-protected solutions are too expensive to make sense.

At the same time, it makes sense for web applications to expect arbitrary and malicious behavior from end-user-controlled clients, such as browsers. Therefore, input validation, correctness control, and output escaping are so important: for example, to prevent SQL injection (SQL injection) and cross-site scripting. However, this usually does not apply protocols protected from Byzantine failures, and the server is simply delegated the authority to decide whether client behavior is acceptable. In peer-to-peer networks where there is no such central authority, protection from Byzantine disruptions is more appropriate.

You can consider software bugs as Byzantine crashes, however, if the same software is used in all nodes, then Byzantine crashes protection algorithms will not save you. Most of these algorithms require a qualified majority of more than two-thirds of normally working nodes (that is, in the case of four nodes, at most one may not work). To solve the error problem with this approach, you would have to use four independent implementations of the same software and hope for the presence of an error in only one of them.

Similarly, it seems tempting for the protocol itself to protect us from vulnerabilities, security breaches, and malicious acts. Unfortunately, in most systems this is unrealistic. If an attacker manages to gain unauthorized access to one node, then it is very likely that he will be able to gain access to the others, since most likely the same software works on them. Consequently, traditional mechanisms (authentication, access control, encryption, firewalls, etc.) remain the main protection against attacks.

Weak forms of "lies."Although we assume that the nodes are predominantly “respectable,” it makes sense to add protection mechanisms against weak forms of “lies” in the software — for example, incorrect messages due to hardware problems, software errors, and incorrect settings. Such mechanisms cannot be considered full-scale protection against Byzantine disruptions, because they cannot be saved from a determined attacker, but these are simple and practical steps to enhance reliability. Here are some examples.

• Damage to network packets sometimes occurs due to hardware problems or errors in the operating system, drivers, routers, etc. Usually, damaged packets are intercepted when checking checksums built into the TCP and UDP protocols, but sometimes they elude checking. Simple measures, such as checksums in the application layer protocol, are usually sufficient to detect packet corruption.
• Applications open to the public must carefully monitor the correctness of the data entered by users, for example, check whether the values ​​are in the acceptable range and limit the length of the lines to avoid denial of service due to the allocation of too large amounts of memory. For a service used inside an organization, behind a firewall, less stringent checks of input data are sufficient, but some simple control of values ​​(for example, during protocol parsing) will not hurt.
• NTP clients can be configured to use addresses of several servers. During synchronization, the client contacts all of them, calculates their errors and makes sure that there is a certain period of time with which most servers agree. If most servers function normally, then an incorrectly configured NTP server that returns an erroneous time is regarded as an anomaly and is excluded from synchronization. The use of multiple servers increases the fault tolerance of the NTP protocol compared to a single server.

System models in practice

Many algorithms have been developed to solve the problems of distributed systems, for example, we will consider the solutions for the consensus problem in chapter 9. To be useful, these algorithms must be able to cope with the various failures of the distributed systems that we discussed in this chapter.

Algorithms should depend as little as possible on the features of the hardware and software settings of the system on which they work. This, in turn, requires formalizing the types of probable failures. To do this, we describe a model of the system - an abstraction that describes the assumptions accepted by the algorithm.

Regarding timing assumptions, three system models are often used.

• Synchronous. It assumes limited network delays, process pauses and clock discrepancies. This does not imply perfect clock synchronization or zero network delay, but simply means that the duration of network delays, process pauses and clock differences never exceed a certain fixed upper limit. The synchronous model is unrealistic for most practical systems, because (as discussed in this chapter) unlimited delays and pauses sometimes occur.
• Partially synchronous. It means that most of the time the system behaves as synchronous, but sometimes it goes beyond the specified duration of network delays, process pauses and clock discrepancies [88]. This is a very realistic model for most systems: for a significant part of the time, the networks and processes function normally - otherwise nothing would work at all. However, it is necessary to take into account this fact: any assumptions regarding timing from time to time crumble to dust. In this case, network delays, pauses and clock errors can reach arbitrarily large values.
• Asynchronous. In this model, the algorithm does not have the right to build any temporary assumptions - in fact, there are not even hours here (so there is no concept of waiting time). Some algorithms can be adapted for an asynchronous model, but it is very limited for the developer.

But, in addition to problems with timing, one should also consider possible node failures. Here are the three most common system models for nodes.

• Failure - Stop Model. Here, the algorithm considers that a node failure can only be fatal. That is, the node is able to stop responding at any time, after which its work will never be resumed.
• The failure-recovery model. It is assumed that a node failure can occur at any time, but then the node will probably begin to respond again after an unknown period of time. This model assumes that the nodes have a reliable storage (that is, a non-volatile storage medium) in which data is not lost during failures (while the data in RAM is considered lost).
• Byzantine (arbitrary) failures. Nodes can do whatever they please, including attempts to trick other nodes and deliberately mislead them, as described in the last subsection.

For simulation of real systems, a partially synchronous failure-recovery model is usually best suited. But how do distributed algorithms cope with it?

Algorithm Correctness

To give a definition of the correctness of an algorithm, I will describe its properties. For example, the results of the sorting algorithm have the following property: for any two different elements of the output list, the element on the left is smaller than the element on the right. This is just a formal way of describing a list sort.

In a similar way, the properties that are required from a correct distributed algorithm are formulated. For example, when generating fencing markers for blocking, you can require the following properties from the algorithm:

• uniqueness - no two requests of the enclosing marker lead to the return of the same value;
• monotonous increase in values ​​- if query x returns a marker tx, and query y returns a marker ty, with x terminating before y starts, then tx <ty;
• accessibility - a node with which a fatal failure did not occur that requested a boundary token finally receives a response to its request.

The algorithm is correct in some model of the system, provided that it always satisfies these properties in all situations that, as we assume, can arise in this model of the system. But does that make sense? If a fatal failure occurs with all nodes or all network delays suddenly drag on indefinitely, then no algorithm can do anything.

Functional safety and survivability

To clarify this situation, it is necessary to distinguish two different types of properties: functional safety (safety) and survivability (liveness). In the example just given, the properties of uniqueness and monotonous increase in values ​​relate to functional safety, and accessibility to survivability.

What is the difference between these two types of properties? Distinctive feature: the presence of the phrase “in the end” in the determination of survivability properties (and yes, you are absolutely right: the final consistency is the survivability property).

Functional safety is often informally described by the phrase “nothing bad happened”, and survivability - “something good will happen over time”. However, it is better not to get carried away too much with such informal definitions, since the words “bad” and “good” are subjective. Genuine definitions of functional safety and survivability are mathematically accurate.

• If the functional safety property is violated, then there is a specific moment in time for this violation (for example, if the uniqueness property is violated, a specific operation can be determined in which a duplicate token is returned). If the functional safety feature is violated, damage has already been done, nothing can be done about it.
• The survivability property, on the contrary, may not be tied to any point in time (for example, a node could send a request but still not receive a response), but there is always hope that it will be satisfied in the future (for example, by receiving a response) .

The advantage of dividing into functional safety and survivability properties is in simplifying work with complex systems models. In the case of distributed algorithms, it is often required that the functional safety properties are always observed, in all possible situations, of a system model. That is, even in the event of a fatal failure of all nodes or the entire network, the algorithm must ensure that it does not return the wrong result (that is, the functional safety properties are observed).

However, clarifications are likely for survivability properties: for example, we can say that the response to a request should be returned only if there is no fatal failure of most nodes and if the network eventually recovered after a service outage. The definition of a partially synchronous model requires that the system gradually return to a synchronous state, that is, any period of network interruption lasts only a limited time, after which it is restored.

Linking system models to the real world

Functional safety and survivability properties, as well as system models, are very convenient for determining the correctness of a distributed algorithm. However, when implementing the algorithm in practice, harsh reality takes over and it becomes clear that the system model is only a simplified abstraction of reality.

For example, the algorithms in the “fatal failure - recovery” model usually assume that the data stored in reliable storage is experiencing fatal failures. However, what will happen if the data on the disk is damaged or the data is erased due to a hardware error or incorrect settings [91]? And if the server firmware contains an error and it stops “seeing” its hard drives after a reboot, although they are connected to the server properly?

The quorum algorithms (see paragraph “Quorum write and read operations” of the subsection “Writing to the database when one of the nodes fails” in Section 5.4) rely on the nodes to store the data whose storage they declared. The possibility of “amnesia” of the node and forgetting the previously saved data violates the quorum conditions, and, consequently, the correctness of the algorithm. Probably, we need a new model of the system with the assumption that reliable storage in most cases survives fatal failures, but sometimes it can lose data. However, it is more difficult to justify this model.

In the theoretical description of the algorithm, it can be stated that certain things simply should not happen - and in non-Byzantine systems, we just make assumptions about which failures can occur and which cannot. However, in practice, sometimes it is necessary to include code in the implementation to handle the case when something that seemed impossible happened even if this processing comes down to printf (“You're out of luck”) and exit (666), that is, the operator will have to rake everything to man. (This, according to some, is the difference between computer science and software engineering.)

This does not mean that theoretical, abstract systems are worthless - just the opposite. They are extremely useful in extracting from the entire complexity of a real system an acceptable set of failures that can be considered in order to understand the problem and try to solve it systematically. You can prove the correctness of the algorithm by demonstrating that its properties are always observed in a certain model of the system.

The proof of the correctness of the algorithm does not mean that its implementation in a real system will always behave correctly. But this is a very good first step, since theoretical analysis will reveal problems in the algorithm that can remain hidden in the real system and manifest themselves only in the event of a collapse of assumptions (for example, regarding timing) due to some unusual circumstances. Theoretical analysis and empirical testing are equally important.

»More information on the book can be found on the publisher’s website
» Table of Contents
» Excerpt

For Khabrozhiteley 20% discount on coupon - Programming