Options Premium Evaluation - Analytical Formulas vs Modeling
Introduction
On the wave of hype of cryptocurrencies, news about trading bitcoin on the global exchanges CME and NASDAQ is slipping. For me, this is a momentous event: the hands of corporations that blew up dotcom and mortgage bubbles reached out to cryptocurrency gold - cryptocurrencies. And in the arsenal of these same corporations, powerful leverage is derivative financial instruments, or derivatives.
Impressed by the recently read stories of the take-offs and metamorphoses of derivatives markets - primarily futures and options contracts, I became interested in the non-trivial pricing of options. It was revealed to me that although the Internet is full of rewrites of articles interpreting the famous Black-Scholes formula, practical tools - websites, technological programs or banal guides for a programmer - are not mathematics, there is not enough Internet on this issue. I had to recall the basics of Terver and adapt rigorous mathematical descriptions in a popular, understandable, first of all, to myself format.
Option Definition
An option is a contract giving the buyer the right (but not the obligation!) To buy or sell the asset traded on the market at the price indicated by him (the buyer of the contract). The seller of the option appoints a premium to the buyer - his reward for the option granted to the buyer of the option to buy or sell the asset at a specified time at a certain price.
An example of an option contract:
- the buyer of the option wants to get the right to buy 10 Ethereum (ETH) at a price of $ 470 for 1 ETH in 30 days.
- Ethereum's current price is $ 450.
Let's say, after 30 days, the Ethereum market rate will rise to $ 500. The buyer of the option will be able to buy 10 Ethereum (10 ETH) at the contract price of $ 470. After that, the buyer who wants to immediately benefit from his transaction will immediately sell Ethereum at a price of $ 500, earning:
10 x (500 - 470) = 300 (USD).
If the price of Ethereum is below $ 470, the buyer of the option will simply refuse a bad deal.
A win-win offer! Of course, for such a wonderful opportunity, the seller will ask for some amount - an option premium.
So, the specification of the option contract:
- In this example, the buyer acquired a European call option in the amount of 10 ETH with a strike price of $ 470 USD with expiration in 30 days.
- “European” - in this context, means that the buyer of the option can make a transaction at a specified price strictly on a certain date - at the time of expiration of the option. There are also “American” options, where the buyer of the contract can exercise it at any time prior to expiration, but consideration of American options is beyond the scope of the article.
- The buyer of the option receives the right to buy the asset (Ethereum) at the indicated price. An option to buy an asset is defined as a call option, for sale - a put option.
- The price at which the option buyer has the right to acquire the asset — in our example, $ 470 — is called the strike price.
- The amount that the buyer of the option will pay the seller is called a premium.
The size of the option premium is the subject of our little research.
How does a seller evaluate an option premium
Calculating the amount of the premium - so that you yourself do not remain on the loser and don’t scare away the potential buyer with a “bullied” price tag - is a real art. At least it was for the time being. Until in 1973, two mathematicians showed the light an elegant formula called by their names - the Black-Scholes formula. About this formula and its impact on the derivatives market, even a popular book, “Quanta. How math wizards earned billions and nearly brought down the stock market. ” Of course, the real story is a little more complicated than “the darkness of ignorance - aloud! - the formula ”... But I am not interested in such global processes, but the immediate question: how much the Black-Scholes formula is applicable for evaluating the“ fair ”option premium calculated for cryptocurrency contracts that are popular with traders?
The Black-Scholes model describes a “standardized” market. Emasculated, freed from sharp price drops, living for years in the same rhythm. Of course, the formula developed for the “ideal” market does not work as well in practice as in theory.
As is customary with traders - where theory is lacking, they turn to empiricism. To the trader “chuyka”, to the “experience”. As a programmer, I am indignant at such ignorance. Therefore, I will give my decision: other people's calculations, a bit of Terver, the magic of Excel and, at the very end, the source code in C #.
Reference calculation - Black - Scholes model
Wikipedia will provide us with the formula . By setting the values of the variables of the option contract and knowing the parameters of the trading asset, we can calculate the “fair” premium.
For further calculations, we need “ideal” data - a price range that has the necessary characteristics.
The real price, as I have already noted, may be a fickle lady: it either stomps on the spot, or suddenly it dashingly breaks off the bat. We need a sample of an ideal series of price data as a standard for subsequent calculations.
Lognormal distribution
The BS model (let's shorten the names of the authors in the title) suggests that the price series describes a lognormal distribution. What does this mean? I will give an example:
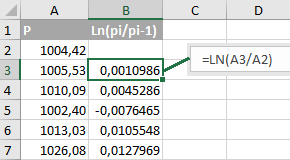
in column A - the price of the abstract asset ABS / USD,
Column B contains the natural logarithm of the quotient
The lognormal distribution describes a price series, the derivative of which, obtained as the natural logarithm of the quotient of dividing the current value with the previous one, has a normal distribution. Difficult. Let me explain in our example: if the values in column B are distributed according to the normal law, then the values of column A describe the lognormal distribution.
How do we get a “lognormal” price range? MS Excel, which I have already used as an example, can generate random numbers that have a uniform (alas, not normal) distribution. There is a simple technique by which we can get a series of normally distributed CB from a uniformly distributed CB. The technique is called the “inverse function method”. Without going into details of the method, I note the following important aspect:
- the inverse function method allows one to obtain a CB with an arbitrary distribution function specified by a function (table), obtaining a CB uniformly distributed in the range from 0 to 1 at the input of the CB.
We need the inverse integral (as it is also called, cumulative) normal distribution function. Such is in Excel: the function "NORM.OBR".
The NORM.OBR function takes the following values: probability, average, standard deviation.
- Probability is the very value from which we build our function. It is strictly greater than 0 and strictly less than 1. We generate 999 values from 0.001 to 0.999 with a step of 0.001 in column A. The values from column A will go to the input of the NORM.OBR function.
- The average is the mathematical expectation of our CB. Let me remind you that we generate a value proportional to the dynamics of our price asset ABS / USD. Positive values correspond to price increases (
), negative - to the fall. If we set the “average” parameter to be greater than zero, our asset will most likely grow (the programmer says: we will conduct a million iterations and we will be guaranteed to see the final price exceeding the initial value). Our choice is an average of 0. Which means “neutral drifting” price of ABS / USD.
- Standard deviation. He will also be discussed later. The value that characterizes the volatility of our asset. Let's take it equal to 0.5% or 0.005. Which roughly corresponds to a change in prices per day by ± 0.5% on average.
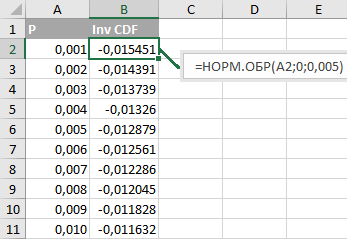
How to interpret this data? Take the first pair of numbers:
“CB will take a value of -0.015451 or less with a probability of 0.001 (0.1%)”.
The second pair: “CB will take the value -0.014391 or less with a probability of 0.002 (0.2%)”. Etc.
Inverse function method: we randomly select a number in the range from 0 to 1 (column A) and find the corresponding inverse cumulative distribution function (column B). Or, in our case, just randomly select a number from column B.
That is, select a value N in the range from 0 to 999 and read the contents of the cell
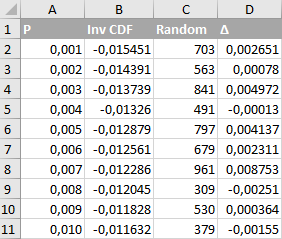
- Cell formula B2: = NORM.OBR (A2; 0; 0.005)
- Cell formula C2: = CASE BETWEEN (0; 999)
- Cell formula D2: = DOUBLE (CLICK (“B”; C2 + 2))
So we got a normally distributed random variable with a mathematical expectation of 0 and a standard deviation of 0.005.
Column D can have any number of values. We need 3650 values - we are going to simulate daily changes in the price of ABS / USD for 10 years. It remains to generate the actual price of ABS / USD.
In column D, we have a number of quantities ∆, and ∆, by the lognormal distribution formula, is defined as
Hence, the prices of ABS / USD, subsequent and previous, will be related by the function
Move column D to a new sheet by copying it and then pasting the values starting from cell A3.
Now specify the initial price of ABS / USD equal to 1000 (USD for 1 ABS) - enter “1000” in cell B2:
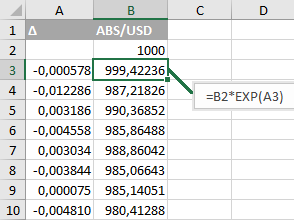
In cell B3, enter “= B2 * EXP (A3)” and copy this value to all subsequent cells - B4: B3652.
On this, the preparation of the initial data is finally completed. Column B contains the price range of our reference asset ABS / USD. A series with the characteristics of a lognormal distribution with a standard deviation of 0.005 (0.5%). I got the following values:

There is no guarantee that if you do exactly the same calculations in MS Excel, you get exactly the same values, since the source data is a random variable. And yet - agree, the chart is quite similar to the stock exchange?
Calculation of premiums according to the formula BS
Since we have “reference” data, we will carry out a “reference” calculation. We consider the premium on the “vanilla” European CALL option:
- current price (S) is 1000,
- strike (X) is 1000. Strike is equal to the current price, this option on the slang is called “vanilla”,
- expiration after 30 days (T),
- transaction volume - one contract.
Our ABS tool is not a stock, not a bond, and not another security. The owner does not rely on any dividends for owning ABS.
The same formula is the formula for calculating the premium for the European Call option (C value):
We analyze the parameters of the formula.
- S and X are already known to us - the current (1000 USD) and strike (1000 USD) asset prices, respectively.
- T is the time to expiration, expressed as part of the year. For example, our ABS contract is traded 365 days a year, like cryptocurrency contracts. Expiration will occur in 30 days, therefore, T = 30/365 ~ 0.082. Another example is an option on EURUSD on the Chicago Stock Exchange, trading approximately 265 days a year. We consider the number of trading days until a specific date - until the day of expiration. Let's say we counted 23 trading days. In this case, the parameter T will be equal to 23/265 or approximately 0.087.
- r is the risk-free interest rate. As we have already noted, for an ABS asset, it is 0.
- σ (sigma) is the historical volatility of the asset. A small digression will be required here.
Historical volatility
For volatility, we take the standard deviation (SD), calculated on a one-year interval. Here is another formula from Wikipedia:
How do we calculate the standard deviation of ABS / USD prices in MS Excel?
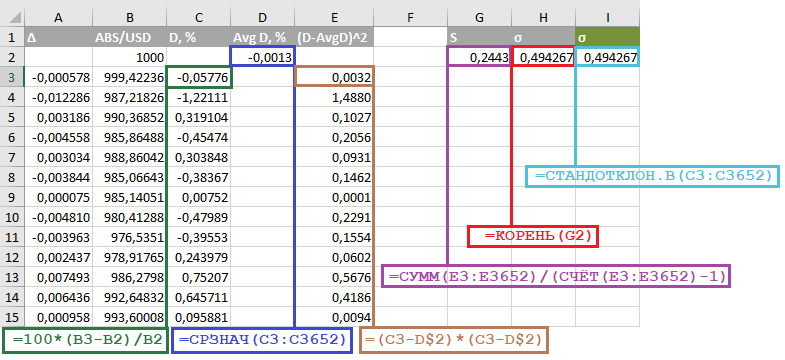
- Column C contains the difference between the current and previous values of the prices ABS, divided by the previous value and multiplied by 100%.
- Cell D2 contains the average of column C.
- Column E contains the squares of the difference between the price deviation (column C) and the average value of the price deviation (cell D2, the second row is “fixed” in the formula with the symbol $).
- Cell G2 - variance, the sum of the squared deviations divided by the number of values minus 1 (SIC!).
- Finally, cell H2 contains the desired standard deviation, the root of the variance (G2).
You can skip part of the calculations: just calculate column C (deviations in percent) and use the Excel function to find the standard deviation (standard) deviation - which we determined in cell I2 - the “STANDOTLINE. B” function.
It remains to recalculate the standard deviation (σ) for the interval of one year. Our ABS / USD trades 365 days a year. The value of σ calculated for one day must be multiplied by the square root of 365:
Where did the square root come from in the formula for converting the daily standard deviation to annual? Those interested are addressing the Internet, look for a random walk model, random walk (RW).
Premium calculation in Excel
Now that we have determined all the parameters of the Black - Scholes formula, we will enter their values and functions in Excel:
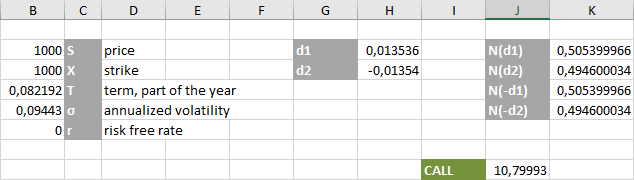
I note right away: I indicate the values of T and σ in absolute terms, not in percent.
- Coefficient formula d1 = (LN (B2 / B3) + B4 * (B6 + B5 * B5 / 2)) / (B5 * ROOT (B4))
- d2 = H2-B5 * ROOT (B4)
- N (d1) = NORM.DISP (H2; 0; 1; TRUE)
- N (d2) = NORM.DISP (H3; 0; 1; TRUE)
- Finally, the premium of the CALL option: = B2 * DEGREE (2.71818; -B7 * B4) * K2-B3 * DEGREE (2.71818; -B6 * B4) * K3
The “fair” premium for the vanilla European CALL option ABS / USD with a strike of 1000 and expiration after 30 days was $ 10.80 per contract.
Premium calculation for “abnormal” price distribution
It was stated above that the B – Sh price model is adequate for the lognormal distribution of the price series. But how close is the “real” market in its characteristics to the similar distribution law of CB? More precisely, how far is the market from it?
Our hypothetical asset ABS / USD is characterized by a normal distribution of logarithms from the private neighboring (current and previous) prices. The graph of the probability density of the appearance of large and small price deviations (logarithms) has a classical form for a normal distribution, approximately the following:
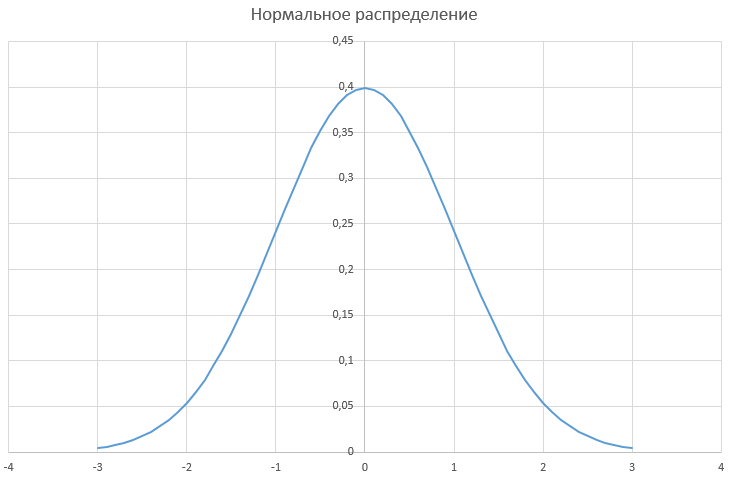
In other words, it has the shape of a bell, with a “steep” peak and “shoulders”, or “tails” that quickly approach the abscissa axis as they move away from the average value (0).
What empirical observations could these “tails” of the normal distribution correspond to for the real market?
Large price deviations are possible, but have an extremely low probability. For the graph above, we can say that a price deviation of + 2% or more has a probability of 5%. A deviation of the price by + 3% or more already has a near-zero probability - some insignificant fractions of a percent.
The “real” market has a slightly different behavior. Specifically, most price changes lie in a rather narrow range, while, however, the probability of significant price fluctuations is significant. The graph of the probability density of price deviations for the “real” market will take the form approximately like this:
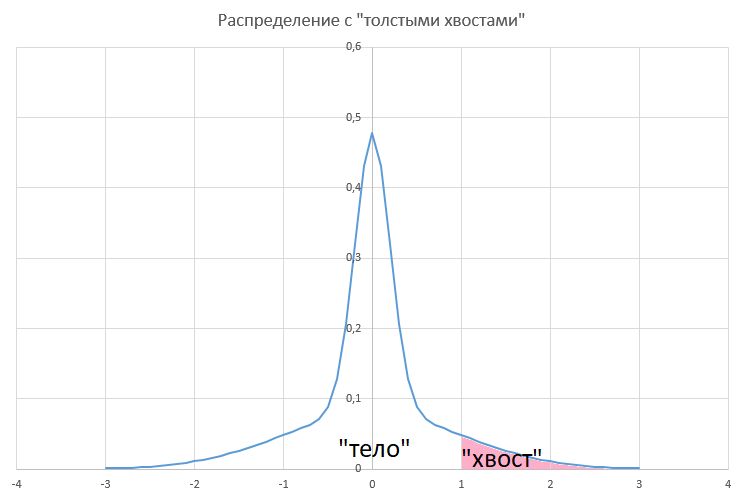
Will the fact that the characteristics of the distribution of daily price deviations for the "real" market differ from the BS model on the accuracy of the calculation?
Obviously affect. The question is, how much will the BS formula be wrong in its assessment of a “fair” premium?
Modeling a “real” price
Now my task is to generate a new price range. A price series, logarithms from private neighboring prices in which they obey a certain “abnormal” distribution - a distribution characterized by “thick tails”. Moreover, I’ll complicate my task a bit.
The final price range should be characterized by the same historical volatility as the ABS / USD price range that we built earlier.
As an example, I’ll give two curves of the distribution density of CB: the normal distribution (brown line) and the “real” distribution (blue line) —that we want to get. With thick and long tails:
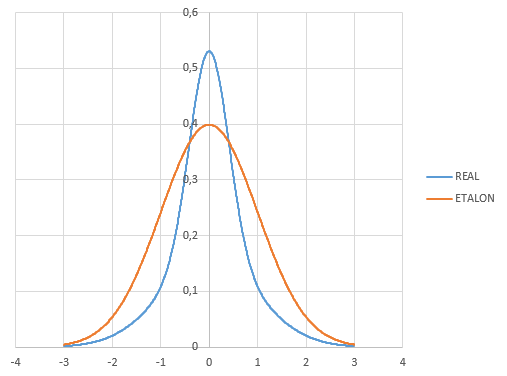
In the normal distribution, we can vary one parameter - the standard deviation (σ). Here are two graphs of the density of the normal distribution with σ equal to 1 and 0.4, respectively:
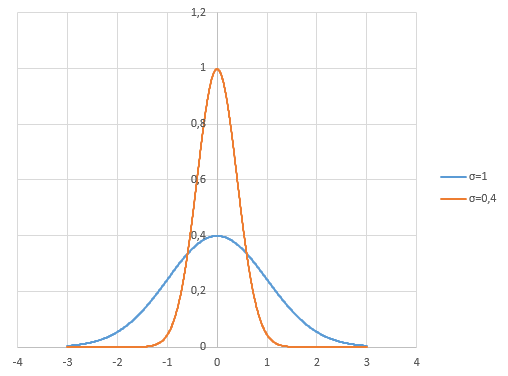
Both graphs are not exactly what we would like. The thin “body” of the graph for the parameter σ = 0.4 is close to the desired. But we would like the “tails” thicker. In other words, a large percentage of deviations concentrating in the vicinity of the average value (0), while the probability of large (2% or more) price deviations is still significant.
Solution: add up two graphs. I will get the very dependence that I cited above in the figure as the “real” probability density of the distribution of prices.
Now we added up the values of the density function of the normal distribution. How to construct a distribution whose density will correspond to the sum of two normal distribution functions with parameters σ = 1 and σ = 0.4?
Obviously (fixed):
- add two (inverse) integral density functions of the normal distribution,
- substitute the argument into the resulting function - uniformly distributed CB.
I will do approximately the same calculations as before, when generating a number of ABS / USD. But now I’ll fill in two columns with the function “NORM.OBR”. The resulting value should have an annual standard deviation of 9.44% - as in the previous example. I will achieve this by conducting several iterations of the selection of parameters, since the result (the generated selection) is non-deterministic:
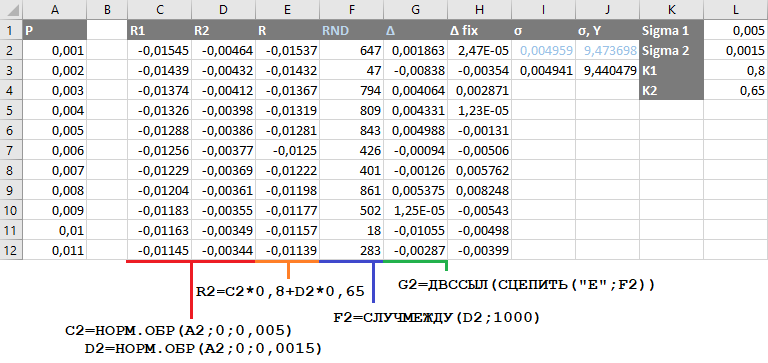
- Columns C (R1), D (R2) contain the inverse normal distribution function with parameters 0.005 and 0.0015, respectively.
- Column E (R) is the weighted sum of these two values - 0.8 x R1 + 0.65 x R2.
- Column F (RND) is a random number in the range from 2 to 1000.
- Finally, the column G (∆) is a cell randomly selected from the column E (R). That distribution that we sought.
It remains to apply the formula to the resulting series:
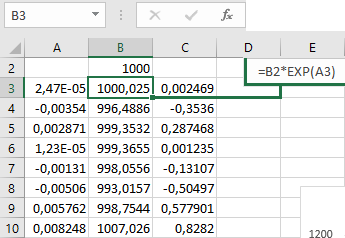
The sum of two normally distributed random variables is copied to column A. In column B, as before, we multiply the previous price value (starting from 1000) by the exponent from CB from column A.
As a result, I got the following price chart WRD / USD:

The premium for the CALL option for WRDUSD under the same conditions of the contract that we have already calculated will remain unchanged, since the parameters in the B – W formula have not changed. Let me remind you of the numbers: the premium for the WRD / USD European CALL option with a strike of 1000 and expiration after 30 days was $ 10.80 per contract.
We have two assets, the price dynamics of which are expressed by different laws:
| ABS / USD | WRD / USD | |
| Price distribution law | lognormal distribution | "Real" distribution |
| Award for the formula B-W | $ 10.80 | $ 10.80 |
| Fair Award | ? | ? |
At this stage, I already lack the capabilities of MS Excel, it is time to move on to programming. To be continued…
