Aliasing is perhaps the most fundamental and most widely discussed artifact of 3D rendering of all time. However, in the gaming community it is often misunderstood. In this article, I will talk in detail about the topic of anti-aliasing, anti-aliasing, AA in real time, especially with regard to games, and at the same time I will explain everything in a fairly simple language.

The various types of aliasing and anti-aliasing discussed in the article will be mainly illustrated using screenshots from the OpenGL program designed to demonstrate variations of aliasing artifacts.

This program can be downloaded here .

Before starting, let me say a few words about performance: since it is the most important aspect of real-time graphics, we will mainly focus on why and how anti-aliasing is implemented today. I will mention performance characteristics, but a rigorous assessment of all the anti-aliasing methods presented in this article in various cases of real use will be too broad a topic for the post.

The nature of aliasing

“If you know yourself and know the enemy, you will not be in danger in a hundred battles”

As Sun Tzu teaches us, in order to defeat the enemy, we first need to understand him. The enemy - forgive me for being too dramatic - aliasing artifacts are the smoothing methods. Therefore, the first thing we need to understand is how and where aliasing comes from.

The term aliasing was first introduced in the field of signal processing, in which it originally described the effect that occurs when different continuous signals become indistinguishable (or begin to distort each other) during sampling. In 3D rendering, this term usually has a more specific meaning: it refers to the many undesirable artifacts that can occur when a 3D scene is rendered for display on a screen consisting of a fixed pixel grid.

In this case, the 3D scene is a continuous signal, and the process of generating color values ​​for each pixel samples this signal to create rendering output. The goal of anti-aliasing methods is to make the output as accurately as possible resemble a scene on a given pixel grid, while minimizing visually distorting artifacts.

Figure 1 shows aliasing in a simple scene consisting of a single white triangle on a black background. At the stage of standardization rasterization, the central position of each pixel is sampled : if it is in a triangle, then the pixel will be painted white, otherwise it will be painted black. The result is clearly visible“ladder” effect , one of the most recognizable aliasing artifacts.

With perfect smoothing for each pixel, it is determined how much of its area is covered by a triangle. If a pixel is 50% closed, then it should be filled with 50% color between white and black (medium gray). If it is closed less, then it should be proportionally darker, if more - then proportionally lighter. A completely closed pixel is white, a completely unclosed pixel is black. The result of this process is shown in the fourth figure. However, performing this calculation in real time is generally an impossible task.

Figure 1 . The simplest aliasing.


1-1. 8x8 grid with marked centers


1-2. 8x8 grid with triangle


1-3. 8x8 grid with rasterized triangle


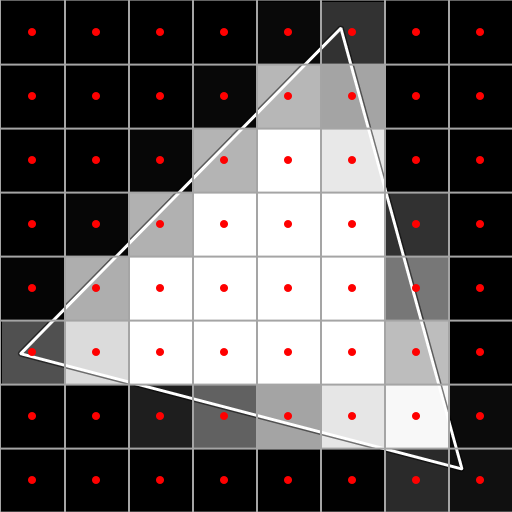
1-4. 8x8 grid with perfectly smooth output

Types of Aliasing

Although all aliasing artifacts can be reduced to the problem of discretization of the representation of a continuous signal on a fixed grid consisting of a limited number of pixels, the specific reasons for their occurrence are very important for choosing an effective smoothing method that eliminates them. As we will see later, some anti-aliasing methods can ideally cope with simple geometric aliasing shown in Figure 1, but fail to fix the aliasing created by other rendering processes.

Therefore, in order to fully discuss the relative strengths and weaknesses of anti-aliasing techniques, we grouped aliasing artifacts that occur during 3D rendering into five separate categories. This grouping depends on the exact conditions for generating artifacts. Figure 2 shows these types of aliasing using a real example rendered using OpenGL.


Figure 2 : Different types of aliasing. From left to right, from top to bottom:
• The only rectangle aligned with the screen with a partially transparent texture.
• “Mill”, consisting of variable white and black triangles aligned relative to the screen.
• Several black lines of various widths, starting from 1 pixel from the top to 0.4 pixels from the bottom, and a white line with a thickness of 0.5, representing a sine wave.
• A cube made up of six flat filled rectangles.
• A sloping plane textured with a high-frequency grass texture.
• A rectangle aligned with the screen with a pixel shader defining the color of each pixel based on the sine function.

The most common type of aliasing that we have already talked about is geometric aliasing . This artifact occurs when a scene primitive (usually a triangle) partially intersects with a pixel, but this partial overlap is not taken into account in the rendering process.

Aliasing transparencyoccurs in textured primitives with partial transparency. The top left image in Figure 2 is rendered using a single rectangle filled with a partially transparent mesh fence texture. Since the texture itself is just a fixed grid of pixels, it must be sampled at the points on which each pixel of the rendered image is superimposed, and a decision must be made for each such point whether transparency is needed in it. As a result, the same sampling problem arises that we have already encountered on solid geometry.

Although it is actually a type of geometric aliasing, subpixel aliasingrequires special consideration, since it poses unique tasks for analytical smoothing methods, which have recently gained great popularity in the rendering of games. We will consider them in detail in the article. Subpixel aliasing occurs when the rasterized structure is superimposed on less than one pixel in the frame buffer grid. This most often happens in the case of narrow objects - spiers, telephone or electric lines, or even swords, when they are far enough from the camera.

Figure 3. Illustration of subpixel aliasing.


3-1. 8x8 grid with marked centers


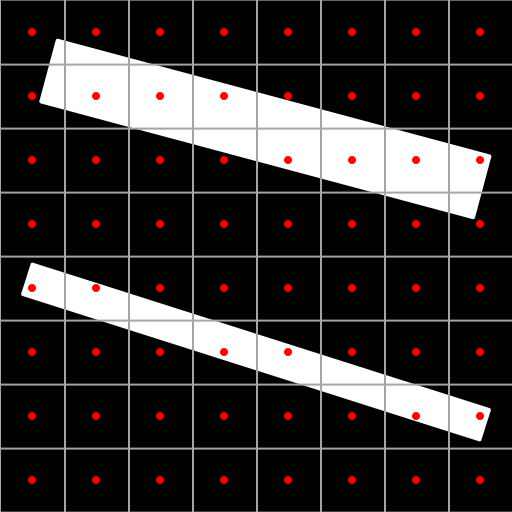
3-2. 8x8 grid with two straight lines


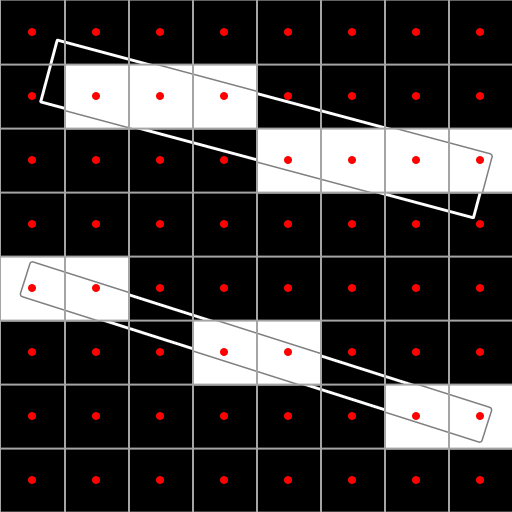
3-3. 8x8 mesh with rasterized line segments, without AA


3-4. 8x8 mesh with a perfectly smooth triangle


Figure 3 shows subpixel aliasing in a simple scene consisting of two line segments. The top one has a width of one pixel, and although during rasterization it demonstrates the familiar artifact - "ladder" of geometric aliasing, the result is still generally in shape consistent with the input data. The bottom segment has a half pixel width. During rasterization, a part of the columns of pixels that it intersects does not have one pixel center within a segment. As a result, it is divided into several unrelated fragments. The same thing can be seen on the straight lines and the curve of the sinusoid in Figure 2.

Texture aliasingarises with insufficient sampling of the texture, especially in cases of anisotropic sampling (these are cases where the damage is strongly inclined relative to the screen). Typically, artifacts created by this type of aliasing are not obvious in still screenshots, but appear in motion as flickering and pixel instability. In Figure 4, this is shown on several frames of the sample program in animation mode.


Texture aliasing can usually be prevented by using mip-texturing and filtering high-quality textures, but it still sometimes remains a problem, especially with some driver versions of popular video processors that sub-sample highly anisotropic textures. It is also influenced by various anti-aliasing methods, therefore it is also included in the demo program.

And finally, shader aliasingoccurs when a pixel shader program, executed for each pixel and determining its color, generates an aliased result. This often happens in games with shaders that create contrast lighting, for example, specular highlights based on a normal map, or with contrast lighting techniques such as cel shading or backlighting. In the demo program, this is approximated by a single shader that calculates the sine function for the texture coordinates and shades all negative results with black and all positive results with white.

Sampling Based Smoothing Techniques

Armed with an understanding of the artifacts of aliasing and all types of aliasing that may arise when rendering a 3D scene, we can begin to study the techniques of anti-aliasing. These techniques can be divided into two categories: techniques that try to reduce aliasing by increasing the number of samples generated during rendering, and techniques that try to mitigate aliasing artifacts by analysis and post-processing of the generated images. The category of sampling-based anti-aliasing techniques is simpler, so you should start with it.

Let's look again at our first example with a triangle in an 8 × 8 pixel grid. The problem with standard rendering is that we only sample the center of each pixel, which leads to the generation of an ugly ladder on edges that are not completely horizontal or vertical. On the other hand, calculating the coverage of each pixel is not possible in real time.

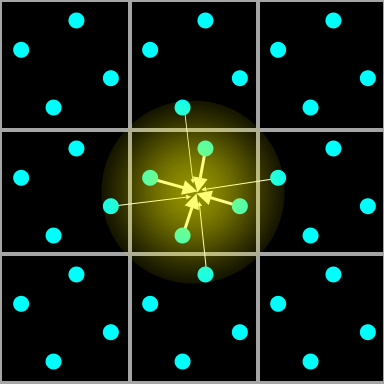
An intuitive solution would be to simply increase the number of samples taken per pixel . This concept is shown in Figure 5.


Figure 5 : A triangle rasterized with four ordered samples per pixel. Pixel

centers are again marked with red dots. However, in fact, four separate places are actually sampled in each pixel (they are marked with turquoise dots). If the triangle does not cover any of these samples, then the pixel is considered black, and if it covers all of them, then white. Here an interesting situation is when only part of the pixels is closed: if one of the four is closed, then the pixel will be 25% white and 75% black. In the case of two of the four, the ratio is 50/50, and with three closed samples, the result will be a lighter shade of 75% white.

This simple idea is the foundation of all sampling-based antialiasing techniques. In this context, it is also worth noting that when the number of samples per pixel tends to infinity, the result of this process will tend to the “perfect” smoothed example shown earlier. Obviously, the quality of the result depends heavily on the number of samples used - but also the performance. Usually, games use 2 or 4 samples per pixel, and 8 or more are usually used only in powerful PCs.

There are other important parameters, the change of which can affect the quality of the obtained results of antialiasing methods based on sampling. Basically this is the location of the samples , the type of samples and grouping of samples .

Sample Location

The location of the samples inside the pixel greatly affects the final result, especially in the case of a small number of samples (2 or 4), which is most often used in real time graphics. In the previous example, the samples are arranged as if they are the centers of the rendered image four times the original (16 × 16 pixels). This is intuitive and easy to achieve by simply rendering larger images. This method is known as ordered grid anti-aliasing (OGAA), and is also sometimes called downsampling. In particular, it is implemented by a forced increase in rendering resolution compared to monitor resolution.

However, an ordered grid is often not optimal, especially for almost vertical and almost horizontal lines, in which aliasing artifacts are just the most obvious. Figure 6 shows why this happens and how a rotated or sparse sampling grid provides much better results:


6-1. Scene with an almost vertical line


6-2. Perfectly smoothed rasterization


6-3. Rasterized with four ordered samples


6-4. Smoothing with four sparse samples

In this nearly vertical case, an ideal four-sample result should have five different shades of gray: black with completely unclosed samples, 25% white with one closed sample, 50% with two, and so on. However, rasterization with an ordered grid gives us only three shades: black, white and 50/50. This happens because the ordered samples are arranged in two columns, and therefore, when one of them is closed by an almost vertical primitive, the other is also likely to be closed.

As shown in the image with sparse sampling, this problem can be circumvented by changing the position of the samples inside each pixel. The ideal sample location for smoothing is sparse. This means that with N samples, no two samples have the same column, row or diagonal in the NxN grid. Such patterns correspond to solutions to the problem of N queens . Antialiasing methods that use such grids are called sparse grid anti-aliasing (SGAA) .

Sample Types

The simplest approach to sample antialiasing based on sampling is that all calculations are performed for the “real” pixel of each sample. Although this approach is highly effective for removing all types of aliasing artifacts, it is also very computationally expensive, because with N samples it increases N times the costs of shading, rasterization, bandwidth and memory. Techniques in which all calculations are performed for each individual sample are called super-sampling anti-aliasing (SSAA) .

Around the beginning of this century, multi-sample anti-aliasing (MSAA) support was built into graphics hardware.being an optimization of supersampling. Unlike the SSAA case, in MSAA each pixel is shaded only once. However, for each sample, the depth and stencil values ​​are calculated, which provides the same smoothing quality on the edges of the geometry as in SSAA, with a significantly lower performance decrease. In addition, further performance improvements are possible, especially for busy bandwidth, if Z-buffer and color buffer compression are supported. They are supported in all modern video processor architectures. Because of the way to optimize MSAA sampling, aliasing transparency, textures, and shaders in this way cannot be directly addressed.

The third type of sampling was introduced by NVIDIA in 2006 in technologycoverage sampling anti-aliasing (CSAA) . MSAA separates shading from pixel-by-pixel depth and stencil calculations, and CSAA adds coverage samplesthat do not contain color, depth, or stensil values ​​- they only store the binary value of the coverage. These binary samples are used to help mix ready-made MSAA samples. That is, CSAA modes add coverage samples to MSAA modes, but it does not make sense to sample coverage without creating multiple MSAA samples. Modern NVIDIA equipment uses three CSAA modes: 8xCSAA (4xMSAA / 8 coverage samples), 16xCSAA (4x / 16), 16xQCSAA (8x / 16) and 32xCSAA (8x / 32). AMD has a similar implementation with 4x EQAA (2x / 4), 8xEQAA (4x / 8) and 16xEQAA (8x / 16). Additional coverage samples usually only slightly affect performance.

Sample Grouping

The last ingredient in sampling-based AA methods is the method of grouping samples, that is, how the individual samples generated during rendering are collected in the final color of each pixel. As shown in Figure 7, various grouping filters are used for this purpose. The picture shows 3 × 3 pixels - turquoise dots indicate the positions of the samples, and a yellow hue indicates the filter for grouping the samples.


7-1. Filter box


7-2. Quincunx Filter


7-3. Tent Filter

The obvious and most common grouping method simply accumulates each sample in a square area representing a pixel with equal weights. This is called a box filter, and is used in all common MSAA modes.

One of the first approaches that attempted to improve the smoothing effect with a small number of samples was quincunx antialiasing. In it, only two samples are calculated per pixel: one in the center, and one shifted half a pixel up and to the left. However, instead of these two samples, five samples accumulate, making up the pattern shown in Figure 7. This leads to a significant reduction in aliasing, but at the same time blurs the whole image, because the color values ​​of the surrounding pixels are grouped into each pixel.

A more flexible approach was introduced in 2007 by AMD in the HD 2900 series of video processors. They use a programmable grouping of samples, which allows you to implement the modes of grouping "narrow tent" and "wide tent". As shown above, each sample does not have the same weight. Instead, a weighting function is used, depending on the distance to the center of the pixel. Narrow and wide options use different filter core sizes. These grouping methods can be combined with a different number of samples, and some of the results obtained are shown in a general comparison. For quincunx AA, these methods are a trade-off between image sharpness and reduced aliasing.

Comparison of AA Sampling

Figure 8 shows a comparison of all the AA methods we examined based on sampling with a different number of samples. The image of “ground truth” shows the closest to the “real”, ideal representation of the scene. It is created by combining 8xSGSSAA and 4 × 4 OGSSAA.

It is worth noting the similar quality of SGMSAA and SGSSAA with the same number of samples for geometric aliasing, and the lack of antialiasing transparency, textures and shaders in the case of MSAA. The disadvantages of ordered sampling patterns, especially for almost horizontal and almost vertical lines, are immediately noticeable when comparing 4x SGSSAA and 2 × 2 OGSSAA. With only two samples per pixel, OGSSAA is limited to only horizontal (2 × 1) or only vertical (1 × 2) AA, and a sparse pattern can to some extent cover both types of edges.

AA methods with sample grouping filters that differ from the regular box filter usually provide better aliasing for the sample, but suffer from the blur effect of the entire image.

One important point to note — especially in light of the subsequent discussion of AA analytic methods — is that all of these sampling methods apply equally well to subpixel aliasing and ordinary geometric aliasing.

Figure 8 : Processing of various types of aliasing with various AA methods based on sampling.


True Image


Without AA


2x MSAA


2x SGSSAA


4x MSAA


4x SGSSAA


8x MSAA


8x SGSSAA


8x MSAA + alpha-to-coverage


2x1 OGSSAA


1x2 OGSSAA


2x2 OGSSAA


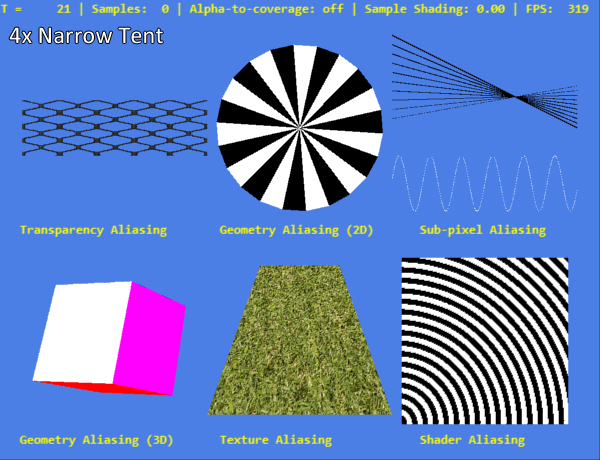
4x Narrow Tent


6x Narrow Tent


6x Wide Tent


8x Wide Tent

Analytical Antialiasing Techniques

Sampling techniques are intuitive and work fairly well with a fairly large number of samples, but at the same time they are computationally expensive. This problem is exacerbated when rendering methods (such as delayed shading) are used, which can complicate the use of efficient hardware-accelerated sampling types. Therefore, other ways to reduce the visual artifacts created by aliasing in 3D rendering are being investigated. Such methods render a normal image with one sample per pixel, and then try to identify and eliminate aliasing by analyzing the image .

Brief introduction and introduction

Although the idea of ​​smoothing computer-generated images has been popularized thanks to a 2009 article by Reshetov on morphological antialiasing (often called MLAA ) [1], it is by no means new. Jules Blumenthal provided a concise description of this technique in his 1983 article for SIGGRAPH “Edge Inference with Applications to Antialiasing”, which is actively used in modern methods [2]:

«Ребро, сэмплируемое по точкам для отображения на растровом устройстве, и непараллельное оси дисплея, выглядит как лесенка. Этот артефакт алиасинга часто возникает в компьютерных изображениях, сгенерированных двухмерными и трёхмерными алгоритмами. Точная информация о ребре часто больше недоступна, но из множества вертикальных и горизонтальных сегментов, формирующих эту лесенку, можно извлечь аппроксимацию исходного ребра с точностью, превосходящей точность растра. Таким образом можно обеспечить сглаживание ребра лесенки.

Такие извлечённые рёбра можно использовать для повторного затенения пикселей, которые они пересекают, таким образом сглаживая извлечённые рёбра. Сглаженные извлечённые рёбра оказываются более привлекательной аппроксимацией реальных рёбер, чем из аналоги с алиасингом».

In 1999, Ishiki and Kunieda introduced the first version of this technique, intended for use in real time, which was performed by scanning pairs of rows and columns of the image, and could be implemented in hardware [3].

In the general case, all purely analytical methods of antialiasing are performed in three stages:

1. Recognition of gaps in the image.
2. Recreating geometric edges from a discontinuity pattern.
3. Smoothing pixels crossing these edges by mixing colors on each side.

Individual analytic antialiasing implementations differ in how these steps are implemented.

Gap detection

The simplest and most common gap detection option is to simply examine the final rendered color buffer. If the color difference of two adjacent pixels (their distance ) is greater than some threshold value, then there is a gap, otherwise it is not. These distance metrics are often calculated in a color space that models human vision better than RGB, for example, in HSL .

Figure 9 shows an example of a rendered image, as well as horizontal and vertical gaps calculated from them.


Figure 9: Gap detection in the color buffer. Left: image without AA. In the center: horizontal breaks. Right: vertical gaps.

To speed up the process of recognizing gaps or to reduce the number of false positive recognitions (for example, in the texture, or around the text in Figure 9), you can use other buffers generated during the rendering process. Typically, a Z buffer (depth buffer) is available for direct and reverse renderer. It stores the depth value for each pixel, and it can be used to recognize edges. However, this only works to recognizesilhouette edges., that is, the external edges of the 3D object. In order to consider edges inside an object, one needs to use one more buffer instead of or in addition to the Z-buffer. For deferred renderers, a buffer is often generated that stores the direction of the normal surfaces of each pixel. In this case, the angle between adjacent normals would be a suitable metric for edge recognition.

Recreating edges and blending

The method of reconstructing geometric edges from gaps varies slightly in different methods of analytical AA, but they all perform similar actions to compare patterns on horizontal and vertical gaps to recognize a typical pattern of "ladder" of aliasing artifacts. Figure 10 shows the patterns used by Reshetov’s description in MLAA and how to recreate edges from them.

Figure 10: MLAA patterns and their recreated edges


Recognized Patterns


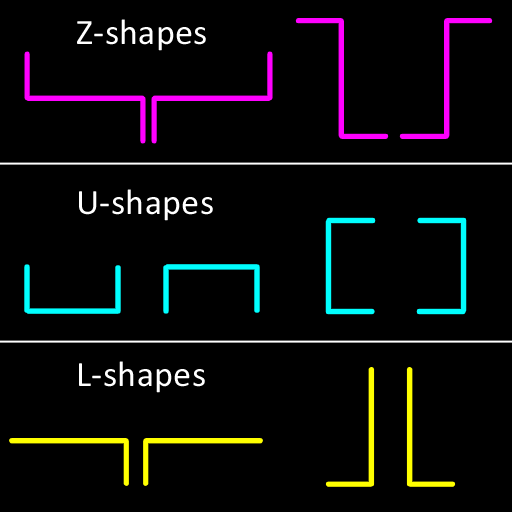
Gap Patterns Used in MLAA

After reconstructing the geometric edges, it is enough to simply calculate how much the top / bottom or right / left pixel along the edge should contribute to the mixed color of the pixel in order to generate a smooth appearance.

Advantages and disadvantages of analytical smoothing

Compared to sampling-based antialiasing methods, analytical solutions have several important advantages. With proper operation (on correctly recognized geometric edges), they can provide a quality equal to the quality of methods based on sampling with a very high number of samples, while spending less computational resources. Moreover, they are easily applicable in many cases in which sampling based AA is more difficult to implement, for example, in the case of delayed shading.

However, analytical AA is not a panacea. An inherent problem with purely analytical methods based on a single sample is that they cannot handle sub-pixel aliasing .

If we pass the pixel structure shown in the upper right corner of Figure 2 to the analytic smoothing algorithm, then he will not be able to understand that the divided groups of pixels actually constitute a line. At this stage, there are two equally unpleasant ways to solve this problem: either blurring the pixels, which reduces visible aliasing, but also destroying the details, or conservative processing of only clearly defined artifacts - "ladders" that are exactly caused by aliasing; at the same time, subpixel aliasing will be preserved and will be distorted.

Another problem with analytical methods is false positives.. When a part of the image is recognized as an aliased edge, but is not really aliased, it will be distorted by blending. This is especially evident in the text, and also requires compromises: a more conservative recognition of edges will lead to fewer false positives, but it will also miss some edges that actually have aliasing. On the other hand, when the edge of recognition of edges is expanded, these edges will also be included, but this will lead to false positives. Since Anatoly Antialiasing basically tries to extrapolate more information from a rasterized image than it actually has, it is impossible to completely get rid of these problems.

Finally, the interpretation of edges by these methods can vary greatly depending on the difference in a single pixel. Therefore, when using single-pixel analytical anti-aliasing methods, flicker and temporary instability of the image can increase or even be added : the only changed pixel in the original image can turn into a smoothed line in the smoothed output data.

Figure 11 shows some of the successful and unsuccessful results of using AA analytical methods using standard FXAA and SMAA1x algorithms as examples. The latter is usually considered the best purely analytical single-pixel algorithm that can be used in real time.

Figure 11: AA Analytical Methods


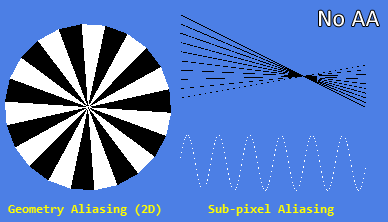
Without AA


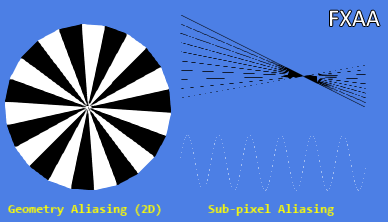
Fxaa


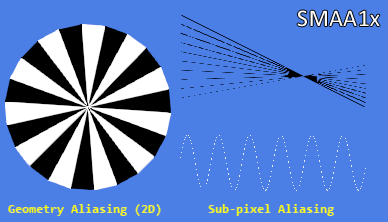
1x SMAA

Comparison of analytical methods of antialiasing

Figure 12 shows a comparison between the results of FXAA, SMAA1x and the “perfect” image, and images without AA, with 4xMSAA and 4xSGSAAA from the previous comparison.

Figure 12: Processing of different types of aliasing using different AA analytical and sampling methods


"Perfect" image


Without AA


4x MSAA


4x SGSSAA


Fxaa


SMAA


Note that unlike the MSAA, these analytical methods are not interested in whether geometry, transparency, or even shader computation were the cause of the aliasing artifacts. All edges are treated the same. Unfortunately, the same applies to the edges of the screen text, although the distortion with SMAA1x and less than with FXAA.

Both methods do not cope with antialiasing in the case of subpixel aliasing, but they handle this failure in different ways: SMAA1x simply decides not to affect individual white pixels of the sine wave at all, and FXAA mixes them with their environment. More desirable processing depends on the context and personal preferences.

More objectively, SMAA1x handles some line angles in a 2D geometry test and the curves in the shader aliasing example are definitely better than FXAA, providing a smoother result that is more aesthetically pleasing and closer to the “perfect” image. This happened thanks to the more complex stage of the recreation of edges and mixing, the details of which are explained in the article on the 2012 SMAA by Jimenez et alia [4].

The future of antialiasing

We got a good understanding of the many antialiasing methods (analytical and based on sampling) that are actively used now in games. It is time to speculate a bit. What anti-aliasing techniques can be seen on the new generation of consoles that raise the bar of technology? How can the shortcomings of existing methods be mitigated, and how can new equipment be allowed to use new algorithms?

Well, the future is already partially here: combined methods based on sampling and analytical antialiasing. These algorithms create several samples of the scene — either through traditional multi- or supersampling or through temporary accumulation between frames — and combine them with analysis, generating the final image with anti-aliasing. This allows them to reduce the problems of sub-pixel aliasing and temporary instability of single-sample purely analytical methods, but still gives much better results on geometric edges than pure sampling methods with similar performance characteristics. A very simple combination of additional sampling and analytical AA can be obtained by combining a single-sample analytical technique like FXAA with sub-sampling from a higher resolution buffer. More complex examples of such methods are SMAA T2x, SMAA S2x and SMAA 4x, as well as TXAA.this article , while NVIDIA has implemented its own approach to TXAA here . It is highly likely that such combined methods will be more widely used in the future.

Another option that has not yet received wide distribution, but has great potential for the future, is to encode additional geometric information during the rendering process, which will later be used at the stage of analytical anti-aliasing. Examples of this approach are Geometric Post-process Anti-Aliasing (GPAA) and Geometry Buffer Anti-Aliasing (GBAA), which demos are available here .

Finally, a common pool of CPU and video processor memory for new console platforms and future PC architectures may allow the use of techniques designed to exploit such shared resources. In a recent article, “Asynchronous Adaptive Anti-aliasing Using Shared Memory,” Barringer and Möller describe a technique that performs traditional single-sample rendering while recognizing important pixels (such as those on an edge) and rasterizing additional sparse samples for them in the CPU [5] . Although this requires a major restructuring of the rendering process, the results look promising.

Reference materials

[1] A. Reshetov, “Morphological antialiasing,” in Proceedings of the Conference on High Performance Graphics 2009 HPG '09 , New York, NY, USA, 2009, pp. 109-116.

[2] J. Bloomenthal, 'Edge Inference with Applications to Antialiasing', ACM SIGGRAPH Comput. Graph., Vol. 17, no. 3, pp. 157–162, Jul. 1983.

[3] T. Isshiki and H. Kunieda, 'Efficient anti-aliasing algorithm for computer generated images', in Proceedings of the 1999 IEEE International Symposium on Circuits and Systems ISCAS '99 , Orlando, FL, 1999, vol. 4, pp. 532-535.

[4] J. Jimenez, JI Echevarria, T. Sousa, and D. Gutierrez, 'SMAA: Enhanced Subpixel Morphological Antialiasing', Comput. Graph. Forum , vol. 31, no. 2pt1, pp. 355–364, May 2012.

[5] R. Barringer and T. Akenine-Möller, 'A ⁴ : asynchronous adaptive anti-aliasing using shared memory', ACM Trans. Graph. , vol. 32, no. 4, pp. 100: 1–100: 10, Jul. 2013.