December 1, 2017 at 17:45

Calltouch multi-channel attribution

    Introduction


    In recent years, the toolkit of a modern Internet marketer is expanding more and more rapidly. Today, in addition to search engine optimization ($ SEO $) and Yandex.Direct contextual advertising and $ Google \: Adwords $ entered into practical use $ e-mail $ channels, social networks, $ Instagram $, remarketing / retargeting, etc. Therefore, the marketer is faced with the task of choosing those advertising channels that will be most effective for a particular project. Calltouch decided to talk about the fact that in addition to the complexity of choosing the optimal advertising channels, it becomes quite difficult to comprehensively evaluate the effectiveness of a particular channel for the subsequent distribution of the advertising budget between them. Column of senior Calltouch Product Manager Fedor Ivanov mthmtcn .

    По оценке Calltouch cложность эта связана в первую очередь с тем, что пользователь со своей стороны обладает по сути тем же самым инструментарием, что и маркетолог: он может прийти на сайт как по прямой ссылке, так и по переходу из соцсетей, из рекламной выдачи Яндекса и. т. д. Более того, прежде чем совершить на сайте целевое действие (конверсию) пользователь может неоднократно посещать сайт из разных «точек входа»: первый раз он перешел на сайт, кликнув по рекламному объявлению ($ CPC $), которое Яндекс выдал по его поисковому запросу, второе посещение было по прямому переходу ($ Direct $), ну а третье (приведшее к конверсии — $ C $ ) было из социальной сети ($ Social $) в этом случае мы наблюдаем цепочку (многоканальную последовательность):

    $ CPC → Direct → Social → C $



    Thus, when evaluating the effectiveness of advertising channels, the marketer first of all needs to answer the question: how to evaluate the contribution of a particular source to the formation of conversion on the site? In another way, this question can be formulated as follows: what will happen to the conversion on the site if one or another marketing channel is excluded? To answer this question, there are a number of methodologies called attribution models. Consider these models in more detail.

    Attribution models


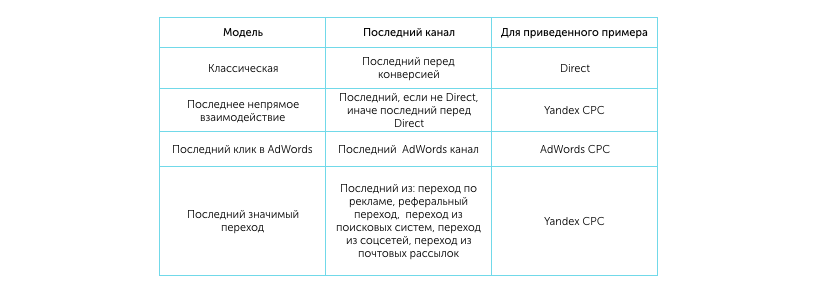
    The attribution model is a way of distributing the conversion “weight” between channels. Depending on the choice of the attribution model, the weight of the channel (source) will be calculated, which can conditionally be considered the contribution that this source made to the formation of the conversion. Practically every user of Yandex Metrics or Google Analytics (the section “multi-channel sequences”) encountered these models. Currently, the following main attribution models are distinguished:

    • By last interaction (last indirect interaction, last click in AdWords, last significant transition) - $ Last \: Click \: Model \ :( LCM) $
    • The first interaction is $ First \: Click \: Model \ :( FCM) $
    • Linear Model - $ Linear \: Model \ :( LM) $
    • Temporary recession - $ Time \: Decay \: Model \ :( TDM) $
    • Based on position - $ Position \: Type \: Model \ :( PTM) $

    As already noted, the main difference between attribution models among themselves is the method of calculating the weight of the channel in the sequence. Let's consider each model in more detail. For clarity, suppose that we have the following multi-channel sequence:

    $$ display $$ AdWords → CPC → Social → Email → Yandex → ​​CPC → Direct → C $$ display $$


    Last click model


    This model, due to its simplicity and intuitive "correctness", is most widely used in practice. In the most general case, within$ LCM $ all models $ 100% $conversion weights are given to the last channel in a multi-channel sequence that preceded the occurrence of the target action. In our case, the classic$ LCM $ the model will give weight $ 100% $ channel $ Direct $ and $ 0% $all other channels.

    In practice, there are different varieties$ LCM $models, they all differ from each other in how they choose the “last” channel. Here is a table that demonstrates the channel selection method depending on the type of model:


    First click model


    In this model $ 100% $ weight is given to the first source in the sequence and $ 0% $to everyone else. In our case, the source will get the maximum weight$ Direct. $ If the model $ LCM $ “Maximizes” the weight of the last channel, which “induces action”, then $ FCM $the model prefers the channel that starts the chain, that is, it “arouses the interest” of the user in the site. This model is also used in practice, although much less frequently than$ LCM. $

    Linear model


    Linear Model ($ Lm $), as well as its generalization and improvement (a model of a temporary recession and based on a position) are united primarily by the fact that within its framework all channels receive their non-zero weight. The difference between the models is only in the way the weight is distributed between all the channels. When$ Lm $all channels receive the same weight (that is, their contributions to the formation of the conversion) are considered equivalent. In our case, the channels$ AdWords \: CPC, $$ Social, $$ Email, $$ Yandex \: CPC, $$ Direct $ will have weight $ 100/5 = $ 20%

    Time decay


    Attribution model $ TDM $ ($ Time \: Decay \: Model $) is based on the assumption that the contribution of the channel is greater, the “closer” to the conversion it is, thus, the weight of the channel is a monotonously increasing function of its position in the chain. Click here for the channel weight calculation formula.

    Position Type Model


    Attribution model $ PTM $ is a combination of three models: $ LCM, $$ FCM $ and $ LM. $ In its framework, the maximum share (usually $ 40% $) receive the first and last interactions in the chain, and the rest (usually $ 20% $) are evenly distributed (as in the linear model) between intermediate channels. In our example, channels$ AdWords \: CPC $ and $ Direct $ will receive $ 40% $ weight and $ Social, $$ Email, $$ Yandex \: CPC $ by $ 6.67%. $

    How to choose an attribution model?


    The choice of attribution model is the most important step in evaluating the effectiveness of advertising. Depending on the model, the analyst may receive completely opposite conclusions about the profitability of a particular channel. This is especially clearly observed in topics where the decision-making process takes a lot of time (for example, in real estate or in automotive topics). A natural question arises: what attribution model should be taken as a reference? Unfortunately, there is no single answer to this question. Only a deep analysis of user behavior on the site (user sessions) will allow you to make an informed decision about choosing a particular method for linking conversions to a traffic source.

    As a rule, the choice stops on the model$ LCM, $ however, in practice, we have encountered situations where replacement $ LCM $ on the $ PTM $with the subsequent distribution of funds between channels, it allowed to significantly increase the effectiveness of marketing activities.

    Separately, it is worth noting that the attribution model is the most important factor that should be taken into account when optimizing contextual advertising. Choosing a model directly affects the statistics that are used to calculate bids. If we consider that each key phrase is a separate advertising channel, then we can significantly enrich the statistics that go to the input of the optimizer, in addition, the analysis of successive user clicks between keywords will increase the efficiency of optimization. A separate chapter of this work will be devoted to the discussion of this topic.

    Прежде чем перейти к описанию подхода, используемого нами для анализа многоканальных последовательностей, приведем «шуточный» пример, который с одной стороны покажет ограниченность классических моделей атрибуции, а с другой стороны позволит сформировать те основные вопросы, на которые следует найти ответ.

    Допустим, целью является C=«увезти девушку к себе домой, чтобы посмотреть кино» .

    Предположим, что мы имеем следующую цепочку действий (по сути каналов), которые привели к желаемой цели:

    Познакомиться с девушкой → Пригласить в кино → Подарить цветы → Гулять вместе в парке → Проводить до дома → Пригласить на свидание в ресторан → Подарить цветы → Угостить ужином → Угостить коктейлем → Угостить еще одним коктейлем →… и еще одним → рассказать анекдот → C

    If we are dealing with a model $ LCM, $then we believe that in order to achieve our goal, in principle, it was enough to do with a joke. If you count within the framework of the model$ FCM, $success is guaranteed as soon as we meet (which is more like the truth in comparison with the same joke). Model$ Lm $assumes that all actions have made an equal contribution. Model$ PTM $postulates that the greatest contribution is made by the fact of acquaintance and a joke (and in equal shares), and the influence of other factors is insignificant. Finally,$ TDM $believes that each of our next actions “fueled” the girl’s interest, thereby increasing the likelihood of achieving the ultimate goal, but still the joke was a decisive factor.

    As we see, none of the classical models can adequately describe the situation considered above, and even more so will not allow to correctly answer the question, which channel (action) turned out to be the most important in reality.

    Now we formulate the main questions that I would like to receive answers from the attribution model:

    • Is it enough to just tell a joke? And if so, how often?
    • How typical is the practice of telling jokes to achieve a goal?
    • What happens if you don’t tell a joke?
    • Is it possible to replace the joke with some other action? If so, which should be replaced?

    For the correct answer to most of the questions posed, it is not enough for us to consider only one sequence. It is necessary to collect some statistics that would allow one to predict user behavior, on the one hand, and would assess the likelihood of conversion on the site for each of the interaction points.

    The model we are considering was originally developed for the combined assessment of multichannel sequences, assuming that the channels are interdependent. It allows you to answer most of the questions formulated above. In addition, we will show how the methods described by us allow us to predict the conversion rate for each key phrase, which is a necessary element in optimizing bids in contextual advertising.

    First of all, we will describe the data format with which our model works.

    Custom sessions


    Suppose that for some period of time we are analyzing $ T $, the site was committed $ M $ transitions, that is, we have data on $ M $user sessions. Each$ i $ session $ S_i $ has a fixed set of parameters (session attributes) $ P $. For our analysis, we need the following set of attributes to be included in the set of all session attributes:

    $ A = \ {SrcType, \: TimeS, \: TimeF, \: URL, \: clientID, \: CVtype \} \ subset P, $


    Where:

    • $ SrcType $- the channel through which the transition to the site was made
    • $ TimeS $- session start time
    • $ TimeF $ - session end time
    • $ Url $ - the address of the page that the user visited when going to the site
    • $ clientID $- unique user identifier
    • $ CVtype $- whether the conversion was made as a result of the session ( $ CV $- Yes, $ N $- not)

    Further, for simplicity, we will assume that the period of time $ [TimeS; TimeF] $ is inside the analyzed period $ T $, so we will remove the attributes $ TimeS, \: TimeF $from the considered set of parameters. It should also be noted that the parameter$ Url $ required only in order to make the transition from the level of channels to the level of key phrases (subject to the presence of markings in $ Url $), which is useful for optimizing bids, but not necessarily for assessing the impact of channels on conversion. Under the channel, we understand the source of traffic, which can include:

    • Yandex CPC
    • Google CPC
    • Facebook
    • Vkontakte
    • Instagram
    • Direct
    • Referal
    • etc.

    For simplicity, we will encode advertising channels as follows: $ c_1, \: c_2, \: ..., \: c_k $, assuming that their number is limited by $ k $.

    Now suppose that$ M $ sessions $ \ Sigma = \ {S_1, S_2, ..., S_M \} $ were initiated $ G \ leq M $by users. Using a unique user ID$ clientID $ many can be broken $ \ Sigma $ on the $ G $ disjoint subsets:

    $ \ Sigma = U_1 \ cup U_2 ... \ cup U_G, $


    Where $ U_i $ many sessions (sorted by increasing end date) with the same $ clientID $, i.e., many chronologically ordered sessions initiated by the same user. Given our assumption that$ [TimeS; TimeF] \ subset T $, then based on the data in $ U_i $ we can match with every $ i $ user following chain of channels:

    $ c_ {i1} → c_ {i2} → ... → c_ {iL_i}, $


    Where $ L_i = | U_i | $ - the number of elements (in fact, the number of user clicks to the site) in the set $ U_i $. The conversion chain presented above is a sequence of traffic sources used by$ i $user in the process of interacting with the site.

    We introduce two additional “pseudo-channels”$ CV $ and $ N $ by the rule:

    • If during the session $ i $ user with source $ c_ {ij} (1 \ leq j \ leq L_i) $ there was a conversion, then after $ c_ {ij} $ add $ CV $having received $...→c_{ij}→CV→...$
    • If as a result of the last current session $i$ with source $c_{iL_i}$ conversion did not happen then after $c_{iL_i}$ add $N$having received $...→ c_{iL_i}→N$

    In addition, we additionally draw attention to the situation when we are dealing with chains of the form:

    $ ...\rightarrow c_{ij}\rightarrow CV\rightarrow...\rightarrow CV\rightarrow... $


    Sequences with such a structure cannot occur according to the rules formulated above, but nevertheless they can occur in a number of cases, for example, in caller topics, when in addition to the session parameters indicated above we have a unique combination:

    $clientID → TelNumber$



    In this case, the first call in the above chain will be a unique call, and all subsequent calls will be repeated calls of the subscriber with the specified $clientID$. Such chains will be taken into account in our model if, in addition to information about the transitions to the site, a “log” of user interactions with the site is maintained, including offline (for example, the call log).

    We note a key feature of the methodology described above for forming user-site interaction chains. It lies in the fact that any chain of interaction (multi-channel sequence) always ends with one of two “events”:$CV$ or $N$. In this event$N$ can only meet at the end of the sequence, while $CV$may appear in any place.

    We give typical examples of sequences formed according to the described rules. For simplicity, we restrict ourselves to 3 different channels$c_1,\:c_2,\:c_3$to which we add $CV$ and $N:$

    • $c_1→N$
    • $c_1→c_2→N$
    • $c_1→CV$
    • $c_1\rightarrow c_2\rightarrow CV\rightarrow c_1\rightarrow N$
    • $c_1\rightarrow c_2\rightarrow CV\rightarrow c_3\rightarrow N$
    • $c_1→c_2→CV→CV$
    • $c_1\rightarrow c_2\rightarrow CV\rightarrow CV\rightarrow c_3\rightarrow N$

    The next step required to build a multi-channel attribution model is to transform the sequences so that the event $CV$as well $N$, could only occur strictly at the end of the sequence (such sequences will be called elementary). To do this, we will “split” the original chains so that at their end always stand$CV$ or $N$.

    We demonstrate this technique using typical sequences as an example:

    • chains 1-4 are already reduced to the "elementary" form
    • chain 5 "split" into: $c_1→c_2→CV$ and $c_1→c_2→c_1→N$
    • chain 6 "split" into: $c_1→c_2→CV$ and $c_1→c_2→c_3→N$
    • chain 7 is “split” into: $c_1→c_2→CV$ and $c_1→c_2→CV$
    • chain 8 is “split” into: $c_1→c_2→CV$, $c_1→c_2→CV$ and $c_1→c_2→c_3→N$

    As a result of splitting, all chains have become "elementary", and now we can begin to describe the model. However, before moving on to this step, at this stage we can already answer the question: how to assess the impact of the channel on the conversion on the site.

    Calculation of the influence of channels on conversion


    Consider the set of $G$ sequences (we assume that all of them are already elementary, that is, they end in $CV$ or $N$. Suppose from the sequences$X$ end in $CV$ and $G$ - $X$ on the $N$. Denote the influence of the channel$c_i$ for conversion on the site for a period of time $T$ through $I(c_i)$, and elementary $j$ chain through $R_j$. Magnitude of influence$I(c_i)$ the channel $c_i$ per conversion, we will count as the number of “lost” conversions in case of removal of the channel $c_i$ of all conversion chains where it’s present, related to the total number of conversions $X$:

    $I(c_i)=\frac{|\{R_j│c_i\in R_j,\:CV\in R_j\}|}{X}$


    Obviously, for any $c_i$ value $I(c_i)$ satisfies the following inequality:

    $0\leq I(c_i)\leq 1$

    moreover $I(c_i)=0$ if and only if the channel $c_i$ is not included in any "conversion" sequence, and $I(c_i)=1$ if and only if removal $c_i$will result in the loss of all conversions on the site. Thus, it’s easy to estimate the new number of conversions that you’ll get after deleting the channel$c_i$:

    $CV_{new}=X*(1-I(c_i))$


    Calculate the effects of channels $c_1$, $c_2$, $c_3$for our example. Total we are observing$8$ conversions (conversion chains) from $13$ elementary chains $R_j$. Channel$c_1$ participates in all conversion chains, which means that its effect on the conversion is $1$: $I(c_1)=1$. Next channel$c_2$ present in $7$ conversion chains, which means $I(c_2)=7/8.$ Finally, $c_3$ is part of one conversion chain, then $I(c_3)=1/8.$

    It is easy to replace that the sum of the channel influences is not equal to unity. For convenience, you can enter a normalization and consider the normalized effect$I_n(c_i)$ channels per conversion:

    $I_n(c_i)=\frac{I(c_i)}{\sum\limits_{i=1}^k I(c_i)}.$


    In this case, obviously

    $\sum\limits_{i=1}^k I_n(c_i)=1.$


    The formula for calculating the influence of the channel on conversion can be easily modified for the case when it is necessary to evaluate the influence of one channel on another. In particular, if the task is to find out how the channel affects$c_i$ on the $c_j$, you can use the following reasoning: user session initiated by the channel $c_i$ leads to a session with a channel $c_j$ as many times as there are chains $R_f$such that in them $c_i$ preceded $c_j$. Then if we denote by$I(c_i,c_j)$ the magnitude of such an effect, then:

    $I(c_i,c_j )=\frac{|\{R_f│c_i,c_j\in R_t\:and\: c_i\:precede\:c_j\}|} {|\{R_t│c_j\in R_t \}|}.$


    In general, the function $I(c_i,c_j)$ not symmetrical: $I(c_i,c_j)≠I(c_j,c_i).$ Sequences $R_f$such that they are simultaneously $c_i$ preceded $c_j$ and $c_j$ preceded $c_i$(i.e., cycles form) can also be taken into account in the denominator of the formula. The normalization introduced earlier is naturally generalized to the more general case just described:

    $I_n(c_i,c_j)=\frac{I(c_i,c_j)}{\sum\limits_{h=1}^k I(c_i,c_h) }.$



    Assessment of changes in basic metrics when a channel is disabled


    After answering the question, how will the number of conversions change when you delete a channel from all chains $c_i$ a completely natural question arises as to how the value of such basic metrics used in analyzing the effectiveness of advertising will change, such as:

    • consumption
    • conversion cost (CPA)

    It is rather difficult to answer these questions without involving additional assumptions. Our basic axiom is that when you delete a channel$c_i$from some chain$R_j$, this chain is interrupted . More precisely, the wording looks like this: if the chain before the removal of the channel looked like:

    $R_j=\{ c_{i1}\rightarrow c_{i2}\rightarrow ...\rightarrow c_{ik}\rightarrow c_i\rightarrow c_{i(k+1)} \rightarrow ...\},$

    then after deleting the channel $c_i$ the chain will be modified in:

    $ R_j \rightarrow R_j^{new}=\{ c_{i1}\rightarrow c_{i2}\rightarrow ...\rightarrow c_{ik}\rightarrow N\}. $


    This assumption means that if you remove the channel that the user used to interact with the site, then there will be no further user interaction with this site.

    To evaluate the basic metrics, we also need to add an indicator such as “transition cost” to the parameters of user sessions. It can be interpreted as the cost paid by the advertiser for the user’s click on this channel, if the channel is free (such as a direct transition), then we assume that the cost of the transition is$0.$ If it is possible to establish only the total cost of the channel (for example, for $SEO$), we will assume that the transition cost in a particular session is equal to the ratio of the total costs per channel to the number of uses of this channel for all sessions. We will denote the transition cost for the channel$c_i$ in the chain $R_j$ through $V_j(c_i)$. Thus, we can estimate the cost$V(R_j)$ single chain $R_j$ in the following way:

    $V(R_j )=\sum\limits_{c_i\in R_j}{V_j(c_i)}.$


    At the same time, the total cost per channel $c_i$ equal to:

    $V(c_i )=\sum\limits_{j:c_i\in R_j}{V_j(c_i)}.$


    The total cost of attracting users to the site when using channels $c_1,c_2,..., c_k$ equal to:

    $V=\sum\limits_{j=1}^G\sum\limits_{c_i\in R_j}{V_j (c_i)} = \sum\limits_{i=1}^k\sum\limits_{j:c_i\in R_j}{V_j(c_i)}.$


    The duality of the formula is explained by different ways of calculating the total costs: in the first case, we summarize the costs for each of the chains for all $G$ chains, and in the second - we summarize the channel costs for all $k$channels.

    To estimate new costs after removing from all channel chains$c_i$ It seems most obvious to use the formula:$V_{new}=V_{old}-\sum\limits_{j:c_i\in R_j}{V(R_j)},$ Where $V_{new}$ - new expense after deleting the channel $c_i$, a $V_{old}$- previous expense. However, such a simple logic does not lead to a correct estimate of costs for the reason that in those chains$R_j$where meets $c_i$, in front of it could be involved other, not remote channels. Thus, for a more accurate estimate, we need to take into account the cost of “truncated” chains. Therefore:

    $V_{new}=V_{old}-\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}.$


    It's obvious that

    $\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}< \sum\limits_{j:c_i\in R_j}{V(R_j)},$


    which means

    $V_{old}-V(c_i)<V_{old}-\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}.$



    The last inequality means that removing any channel $c_i$As a rule, it leads to the appearance of new chains with a certain value, which obviously will not bring conversions. Thus, we can estimate the loss$Loss(c_i)$ from removing the channel (the cost of all “truncated” chains), as well as saving $EC(c_i)$ as the cost of all "non-essential" transitions that would have occurred if the channel were saved in chains:

    $Loss(c_i)=\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)},$


    $EC(c_i )=\sum\limits_{j:c_i\in R_j}{V(R_j)}-Loss(c_i).$


    Now, after we learned how to measure the change in spending after deleting the channel $c_i$, we can estimate the new conversion cost that would have occurred if there was no channel:

    $ CPA_{new}=\frac{V_{new}}{CV_{new}}=\frac{V_{old}-\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}}{X*(1-I(c_i))} $


    If we assume that before the removal of the channel, we had the previous conversion cost:

    $CPA_{old}=\frac{V_{old}}{X}$

    and the goal of removing the channel is to reduce the cost of conversion, the decisive rule may be as follows:

    $CPA_{new}-CPA_{old}<0.$


    That is, if the removal of the channel leads to a decrease in the cost of conversion (with a reasonable decrease in their number), then it can be excluded from the chain and stop spending the budget on it.

    In addition, you can estimate the cost of "lost conversions" when you delete a channel:

    $CPA_{loss}=\frac{V_{old}-V_{new}}{X*I(c_i)},$

    therefore instead of the rule $CPA_{new}-CPA_{old}<0$ you can use another: if the ratio

    $CPA_{loss}>CPA_{old},$

    then deleting the channel $c_i$will reduce the overall cost of conversion on the site.

    Now we proceed to describe the basic model required to calculate the probability of channel conversion.

    Model description


    Прежде чем мы приступим к описанию многоканальной модели атрибуции, нам бы хотелось сослаться на замечательные статьи Сергея Брыля, и вторую статью, в которых автор использовал красоту и функциональность марковских цепей для описания многоканальной атрибуции. В рамках данной статьи мы более подробно описали основные моменты, связанные с расчетом вероятности конверсии в рамках марковских процессов, а также предложили эффективный метод вычисления вероятности конверсии – на основании стохастических матриц.

    We will offer two alternative interpretations of the multichannel attribution model: graph and matrix. The first allows you to clearly describe the model, while the second allows you to effectively calculate the required characteristics. We show that both descriptions actually represent the same random process, which is called the Markov process, and the model corresponding to the process, the Markov chain.

    Graph model


    A graph is an abstract mathematical object, which is a set of graph vertices and a set of edges, that is, connections between pairs of vertices. For example, for many peaks you can take many airports served by a certain airline, and for many edges take regular flights of this airline between cities.

    A graph is called oriented if each of its edges has a direction, i.e., it is essentially a vector: for an edge it is precisely indicated from which vertex it originates and to which it ends.

    A graph is called weighted if each of its edges is assigned a numerical value called a weight. A typical example of a weighted oriented graph is a network of roads between cities (vertices of the graph), where by the weight of an edge (road) we understand its length.

    In order to represent the set of chains in the form of a graph, we need to fix two sets: the set of vertices$V$ and many connections $E$between them. The peaks will be marketing channels and two additional events:

    $ V=\{c_1,\: c_2,\: ...,\: c_k,\:CV,\:N\}. $


    As $E$ we will choose pairs of interconnected elements from $V$. For the elementary chains considered above, we have:

    $ V=\{c_1,\:c_2,\:c_3,\:CV,\:N\},\\ E=\{(c_1,N),\:(c_1,c_2),\:(c_2,N),\:(c_1,CV),\:(c_1,c_2),\:...,\:(c_3,N)\}. $



    In view of the fact that in the set $E$matching elements may occur, the resulting graph may have multiple (duplicated) edges.



    As can be seen, even for a small number of sessions, such a graphical representation is rather cumbersome, which complicates the analysis. Some simplification can be achieved by replacing duplicated ribs with one rib, taking the number of takes as a weight. Then the original graph is transformed into a directed weighted graph:


    This graph is already more suitable for analysis. Our next goal is to convert the edge weight to probabilistic notation. Replace the weight of the edge connecting the two vertices with the probability of transition from one vertex to another.

    In particular, consider the top$c_1$. The following vertices of the graph are reachable from it:$c_2,\:CV,\:N$. Total from the top$c_1$ was recorded $1+11+2=14$ transitions, moreover $11$ of which were in $c_2$, $2$ - in $N$ and one in $CV$. Then if we denote$P(c_1,c_2),\:P(c_1,N),\:P(c_1,CV)$ - probabilities to move from $c_1$ in $c_2,\:CV,\:N$ accordingly, then:

    $P(c_1,c_2)=\frac{11}{14},\: P(c_1,N)=\frac{2}{14}=\frac17,\: P(c_1,CV)=\frac{1}{14}.$


    Easy to replace that $P(c_1,CV)$ Is the probability of source conversion $c_1$ in the classic model $LCM.$ It becomes obvious that the model $LCM$does not take into account the large amount of statistics that we can collect by analyzing user sessions. If we make calculations for all the remaining vertices, then our graph will be converted to:



    Based on this model, we can calculate the total conversion probability for a particular channel. For calculation, the following recursive formula is used:

    $ P_{full}(c_i,CV)=\sum\limits_{c_j:c_i\rightarrow c_j}{P(c_i,c_j)P_{full}(c_j,CV)} $


    Смысл этой формулы в том, что для того, чтобы рассчитать полную вероятность конверсии некоторой вершины, требуется выбрать все вершины, достижимые из данной, затем рассчитать вероятности перехода в эти вершины из исходной, а затем для каждой достижимой вершины снова рассчитать полную вероятность конверсии. Данная формула тут же дает полную вероятность конверсии, если граф является однонаправленным, т. е. если есть ребро, соединяющее вершины $c_i$ и $c_j$, но отсутствует ребро, которое соединяет $c_j$ c $c_i$. В противном случае указанная выше формула задает систему линейных уравнений, количество неизвестных в которой равно количеству «возвратных» ребер в графе.

    Например, рассчитаем полную вероятность конверсии $P_{full}(c_1,CV)$ для источника $c_1$.

    Так как $c_1$ связан с $c_2,\:CV,\:N$, но вероятность перейти из $N$ в $CV$ равна нулю, а вероятность перейти из $CV$ в $CV$ equal to 1, then:

    $ P_{full}(c_1,CV)=P(c_1,c_2)*P_{full}(c_2,CV)+P(c_1,CV)*1=\frac{11}{14}*P_{full} (c_2,CV)+\frac{1}{14}.$


    In turn from $c_2$ can return to $c_1$ or go to $c_3,\:CV,\:N$, which means:

    $ P_{full}(c_2,CV)=P(c_2,c_1)*P_{full}(c_1,CV)+P(c_2,c_3)*P_{full} (c_3,CV)+ P(c_2,CV)*1, \\ P_{full}(c_2,CV)=\frac{1}{11}*P_{full}(c_1,CV)+\frac{3}{11}*P_{full}(c_3,CV)+\frac{6}{11}, $


    then

    $ P_{full}(c_1,CV)=\frac{11}{14}*\Bigl(\frac{1}{11}*P_{full}(c_1,CV)+\frac{3}{11}*P_{full} (c_3,CV)+\frac{6}{11}\Bigr)+\frac{1}{14}. $


    For convenience, we denote $P_{full}(c_1,CV)=x$, then we obtain the following linear equation:

    $ х=\frac{11}{14}*\Bigl(\frac{1}{11}*x+\frac{3}{11}*P_{full}(c_3,CV)+\frac{6}{11}\Bigr)+\frac{1}{14}. $


    Now calculate $P_{full}(c_3,CV)$. From source$c_3$ can only go to $CV$ or $N$. Then

    $ P_{full}(c_3,CV)=\frac{1}{3}. $


    Finally, we have the following equation:

    $ x=\frac{11}{14}*\Bigl(\frac{1}{11}*x+\frac{3}{11}*\frac{1}{3}+\frac{6}{11}\Bigr)+\frac{1}{14}. $


    Where from

    $ x= P_{full}(c_1,CV)=\frac{8}{13}=0.6154. $

    .
    The main advantage of the above model is its visibility, while obvious disadvantages (which can be seen even with a simple example) include high computational complexity for the case of a large number of traffic sources. Moreover, if different keywords are used as sources, the volume of calculations increases by orders of magnitude, which will make all subsequent calculations unrealizable. In addition, if we allow the possibility of transitions in a graph of the form:$...\rightarrow c_i\rightarrow c_i\rightarrow ... $(i.e., allow loops), the system of equations becomes nonlinear, which significantly complicates the finding of the required probabilities. In the next section, we proceed to consider the matrix model and show effective methods for calculating the formulas for the total probability.

    Matrix model


    In the previous chapter, we examined the graph model of multichannel attribution. In order to convert it to a more convenient form for calculations, we again consider a set of$k$ channels $c_1,c_2,...c_k$ and two additional "pseudo-channels" $CV$, $N$. Let me remind you that in the graph model they played the role of vertices.

    From the observed sequences compiled for each of the users, we can easily calculate the transition probabilities (in other words, conditional probabilities)$P(c_i,c_j),\:P(c_i,CV),\:P(c_i,N)$. As noted earlier, we assume that$P(N,c_i)=P(CV,c_i)=0$ and $P(N,N)=P(CV,CV)=1$. Then you can make a square matrix of size$(k+2)\times(k+2)$whose elements are conditional probabilities $P(c_i,c_j),\:P(c_i,CV),\:P(c_i,N),\:P(N,c_i),\:P(CV,c_i):$
    and $P(N,N),\:P(CV,CV)$:

    $ H=\begin{pmatrix} P(c_1,c_1)& P(c_1,c_2)& …& P(c_1,c_k)& P(c_1,CV) & P(c_1,N) \\ P(c_2,c_1)& P(c_2,c_2)& …& P(c_2,c_k)& P(c_2,CV) & P(c_2,N) \\ …&…&…&…&…&… \\ P(c_k,c_1) & P(c_k,c_2) & … & P(c_k,c_k) & P(c_k,CV) & P(c_k,N) \\ 0&0&…&0&1&0 \\ 0&0&…&0&0&1 \end{pmatrix} $



    In particular, for the above example, we get:

    $ H=\begin{pmatrix} 0&\frac{11}{14}&0&\frac{1}{14}&\frac{2}{14}\\ \frac{1}{11}&0&\frac{3}{11}&\frac{6}{11}&\frac{1}{11}\\ 0&0&0&\frac13&\frac23\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{pmatrix} $



    It is easy to see that for any $i$ matrix rows $H$ fair:

    $ \sum\limits_{j=1}^k{P(c_i,c_j)}+P(c_i,CV)+P(c_i,N)=1. $


    A matrix for which this condition is satisfied is called stochastic. It is known that an arbitrary stochastic matrix defines some random process called Markov process. Let us give such a process a more formal (although not rigorous from a mathematical point of view) definition.

    A Markov process is such a random process with a certain number of states that the probability of transition to the next state depends only on the current state in which the system is located.

    Thus, the transition process we are considering between the various marketing channels can be considered a Markov process, determined by a matrix of transition probabilities$H$. The model defined in this way answers a number of important questions, in particular:

    • What is the probability of moving from a state $c_i$ to state $c_j$ behind $t$ steps?
    • How the probability distribution of being in each channel through $t$ steps?

    In our applied problem of estimating the conversion probability of each channel, we need to answer a particular case of the first question:

    What is the total probability of passing from the state (channel)$c_i$ in $CV$?

    The Markov theory of random processes allows us to give a very simple answer to this question (in the case where the states$CV$ and $N$no transitions to any other states are possible): to calculate this probability, it is necessary to raise the matrix to an infinite degree and take the value standing at the position$(i,k+1)$:

    $ P_{full}(c_i,CV)=\lim_{t\rightarrow \infty}H^t (i,k+1). $


    It can be rigorously proved that for the case when from the states $CV$ and $N$no transitions to any other state are possible; this limit exists. Of course, in practice, we cannot operate with the “infinite” degree of the matrix. However, instead of "infinity", as a rule, it is enough to take a sufficiently large degree of two. Convenience of raising a matrix to a power$2^t$ lies in the fact that it is required to produce exactly matrix multiplications $H$to myself.

    In fact, let, for example,$t=8$. Then to calculate$H^{2^8}=H^{256}$ it is enough to calculate:

    $H*H=H^2,\\ H^2*H^2=H^4,\\ H^4*H^4=H^8,\\ H^8*H^8=H^{16},\\ H^{16}*H^{16}=H^{32},\\ H^{32}*H^{32}=H^{64},\\ H^{64}*H^{64}=H^{128},\\ H^{128}*H^{128}=H^{256}. $


    We show on our example the speed of "convergence" of the limit to the probability we need:



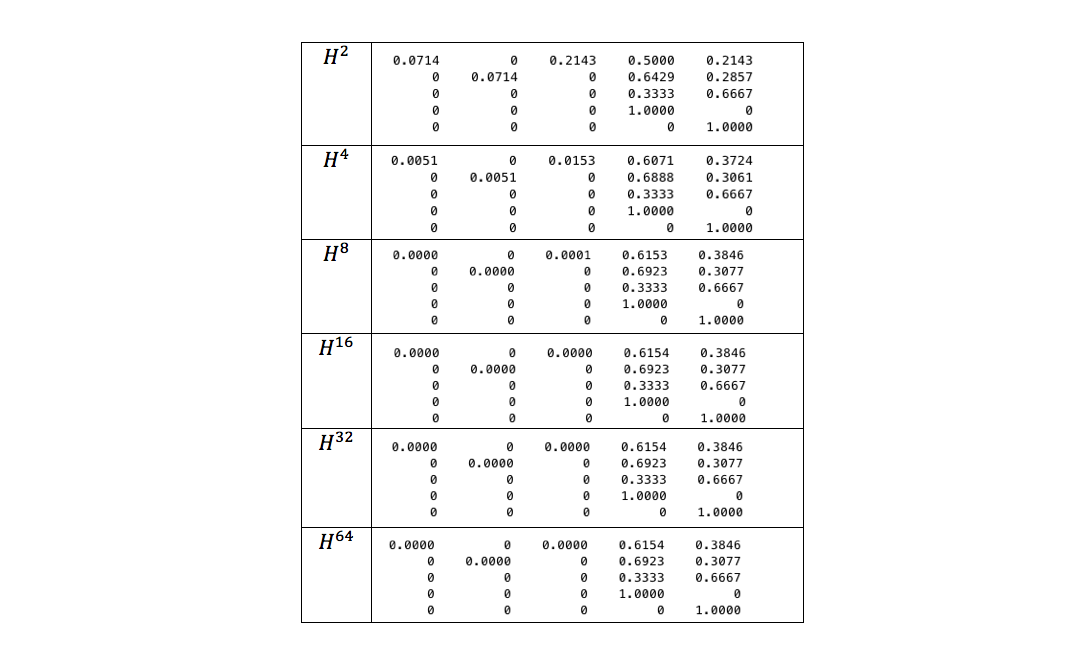
    As can be seen from the table, for$H^8$ calculated probability $P_{full}(c_1,CV)$differs from the exact value that we previously obtained on the basis of the graph model, in 4 decimal places. Probability values ​​calculated for$H^{16}$, $H^{32}$, $H^{64}$and completely coincide. Thus, in this case it was enough to limit ourselves to calculating$H^8$that requires everything $3$matrix multiplication. Thus, the rate of convergence of the limit to the required probability is high enough, which makes this model effective in practical applications.

    From channel assessment to optimization


    The constructed analytical model allows us to solve 3 main problems:

    • Assess the impact of the channel on the conversion on the site
    • Assess the mutual influence of channels on each other
    • Assess the likelihood that using the channel will lead to a conversion on the site

    When designing a conversion optimizer that allows you to manage bids in contextual advertising based on their performance so that they achieve the desired $KPI$ (key performance indicators), you need to evaluate the conversion rate $CR$for each keyword phrase. As we noted, the choice of a particular conversion attribution model directly affects the calculation of the conversion rate not only at the level of the advertising channel, but also at the level of the key phrase. Traditionally, optimizers work with the model$LCM$or its modifications. Previously we showed limited ability$LCM$to predict the conversion rate (as a rule, it underestimates it, since it takes into account only the direct connection keyword conversion, not analyzing intermediate transitions).

    The presented conversion attribution model is free from these drawbacks, although it requires significantly more computing resources to calculate probabilities. The flexibility of the described approach also lies in the fact that we can use any integral attribute of a session as a “channel”.

    In particular, we consider the parameter$URL$, which was not used by us earlier in the calculations. $URL$contains information about the page on the site that the user goes to at the beginning of the session. If all ads are marked on the advertising account associated with the site$UTM-$tags, then we can significantly deepen our analytics.

    $UTM$labels are parameters (variables) containing additional data that are added to$URL$landing (landing) page and allow you to transfer additional information about traffic characteristics to web analytics systems. Consider a typical example$UTM$ tags, for example in the format accepted by the company $Calltouch$:
    site.ru/?utm_source=YD&utm_medium=cpc&utm_content=kvartiry_ceny&utm_campaign=YD_KVARTIRY_POISK_MSK&calltouch_tm=yd_c:{campaign_id}_gb:{gbid}_ad:{ad_id}_ph:{phrase_id}_st:{source_type}_pt:{position_type}_p:{position}_s:{source}_dt:{device_type}_reg:{region_id}_ret:{retargeting_id}_apt:{addphrasestext}

    На основе динамических параметров, которые содержатся в фигурных скобках, мы можем, в частности, отследить «путь» клика на рекламное объявление с точностью до ключевой фразы, которая инициировала показ рекламного объявления, на которое кликнул пользователь. Мы можем выбрать любой «разумный» динамический параметр (или их связку) в качестве канала. В частности, если выбрать в качестве канала параметр $\{phrase_{id}\}$, then we can track the user's transition chain to the site for different keywords. If we repeat all the arguments for this type of channel, the model will allow us to calculate the full probability of conversion for each key phrase.

    The resulting array of conversion rates can be used as input to the conversion optimizer.

    Conclusion


    The article gives an overview of currently used classic models of conversion attribution. In addition, a multi-channel attribution model based on Markov processes (chains) is described, which allows you to comprehensively evaluate both the probability of conversion for each advertising channel and calculate the channel’s effect on conversion on the site. Demonstrated approaches to adapt the built model to optimize bids in contextual advertising.
    Tags:

    Also popular now: