Fractal Gerasimov. Found a pattern. Black table
I discovered this pattern when I looked at the post of the user xcont . Stumbling upon this publication , I noticed that the patterns are repeated not only with an increase in the scale of Fibonacci numbers.

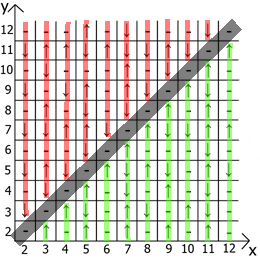
I wondered whether there is a pattern in these patterns. But having only 2 parameters x and y , I decided that I need to designate something else, common among all the patterns obtained. Then I noticed that if we take the first 4 squares on the field, in any case we get 3 options for the beginning of the pattern, if the line goes:
up (↑)

down (↓)

or not * (-)

For the notation, I decided to use these symbols ↑, ↓, conventionally calling them spins (like the spin of a particle). And here I started to create a table of the dependence of these spins to x , y .
First, let's see if there is a pattern if we change only y , x we take 4

And now about the properties.
We see the sequence of spins - ↑ - ↓ - ↑ - ↓ - ↑ - ↓ The
pattern repeats with a certain sequence
y = 3,7,11 ... ( ↑ )
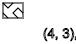
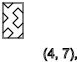
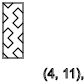
y = 5,9,13 ... ( ↓ )
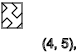
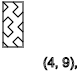
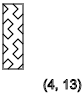
y = 2,4,6,8,10,12 ... ( - )
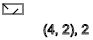
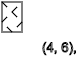
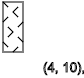
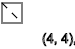
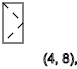
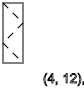
The same is true if we get x = 3, we see the sequence of spins ↑ - ↑ ↓ - ↑ ↓ - ↑ ↓ - ↑ ↓

y = 2,5,8,11 ... ( ↑ )
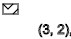
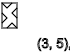
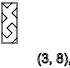
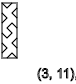
y = 4,7,10,13 ... ( ↓ )

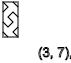
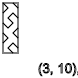
y = 3,6,9,12 ... ( - )
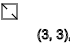
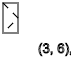
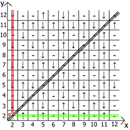
I thought that you can systematize these sequences and make a table of these spins and this is what I got.
I present to you, "Black Table".
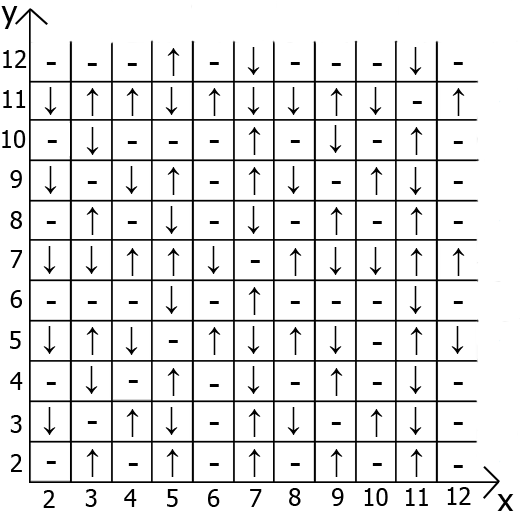
The most interesting is that this table has its own dependencies and properties.
To start a pair derive formulas: →
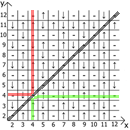
if x is even and y is an even → -, also if x ⋮ y or y ⋮ x → -
x = y → -
x = y + 1 → ↑
x = y-1 → ↓
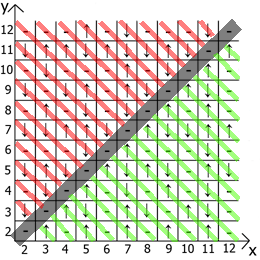
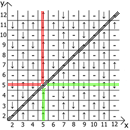
And now about the properties of the table itself, if we take x = y as a reference point, then in any direction we have mirrored sequences (marked by red and green lines ).
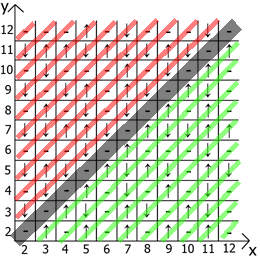
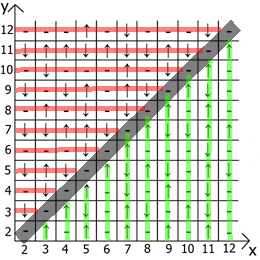
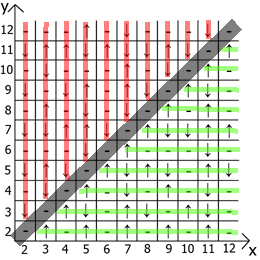
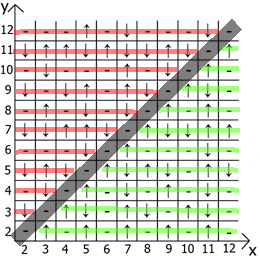

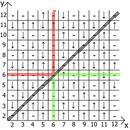
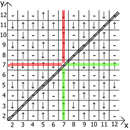
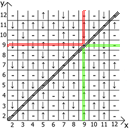
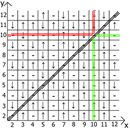
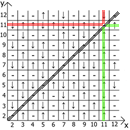
Actually find application and use. My table is lined up to 12, since initially I did all this on paper.

But with the help of a JavaScript algorithm, you yourself can check for larger values.
PS I do not know how it can be used, but perhaps this algorithm can be applied on a quantum computer.
Links: one and two .

I wondered whether there is a pattern in these patterns. But having only 2 parameters x and y , I decided that I need to designate something else, common among all the patterns obtained. Then I noticed that if we take the first 4 squares on the field, in any case we get 3 options for the beginning of the pattern, if the line goes:
up (↑)

down (↓)

or not * (-)

For the notation, I decided to use these symbols ↑, ↓, conventionally calling them spins (like the spin of a particle). And here I started to create a table of the dependence of these spins to x , y .
First, let's see if there is a pattern if we change only y , x we take 4

And now about the properties.
We see the sequence of spins - ↑ - ↓ - ↑ - ↓ - ↑ - ↓ The
pattern repeats with a certain sequence
y = 3,7,11 ... ( ↑ )
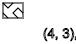


y = 5,9,13 ... ( ↓ )



y = 2,4,6,8,10,12 ... ( - )
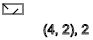


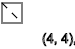


The same is true if we get x = 3, we see the sequence of spins ↑ - ↑ ↓ - ↑ ↓ - ↑ ↓ - ↑ ↓

y = 2,5,8,11 ... ( ↑ )
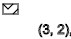



y = 4,7,10,13 ... ( ↓ )



y = 3,6,9,12 ... ( - )
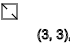



I thought that you can systematize these sequences and make a table of these spins and this is what I got.
I present to you, "Black Table".

The most interesting is that this table has its own dependencies and properties.
To start a pair derive formulas: →
if x is even and y is an even → -, also if x ⋮ y or y ⋮ x → -
x = y → -
x = y + 1 → ↑
x = y-1 → ↓
And now about the properties of the table itself, if we take x = y as a reference point, then in any direction we have mirrored sequences (marked by red and green lines ).















Actually find application and use. My table is lined up to 12, since initially I did all this on paper.


But with the help of a JavaScript algorithm, you yourself can check for larger values.
PS I do not know how it can be used, but perhaps this algorithm can be applied on a quantum computer.
Links: one and two .
