Earth imagery

Satellite image in false colors (green, red, near infrared) with a spatial resolution of 3 meters and an overlaid building mask from OpenStreetMap (satellite constellation PlanetScope)

Hello, Habr! We are constantly expanding the data sources that we use for analytics, so we decided to add satellite images as well. Our satellite imagery analytics is useful in products for entrepreneurship and investment. In the first case, geodata statistics will help you understand where to open retail outlets; in the second, it allows you to analyze the activities of companies. For example, for construction companies, you can calculate how many floors were built in a month, for agricultural companies - how many hectares of crops have grown, etc.

In this article I will try to give an approximate idea of ​​space imagery of the Earth, I will talk about the difficulties that you may encounter when starting to work with satellite imagery: preprocessing, algorithms for analysis and the Python library for working with satellite imagery and geodata. So everyone who is interested in the field of computer vision, welcome to cut!

So, let's start with the spectral regions in which the satellites are shooting, and consider the characteristics of the shooting equipment of some satellites.

Spectral signatures, atmospheric windows and satellites

Different terrestrial surfaces have different spectral signatures. For example, fresh basaltic lava and asphalt reflect different amounts of infrared light, although they are similar in visible light.


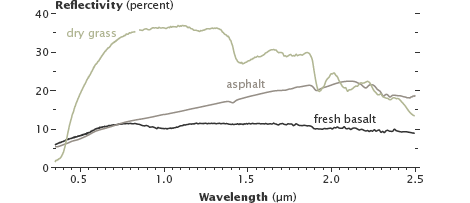
Reflectivity of dry grass, asphalt and fresh basaltic lava.

Like the Earth’s surface, the gases in the atmosphere also have unique spectral signatures. However, not every radiation passes through the Earth’s atmosphere. The spectral ranges passing through the atmosphere are called “atmospheric windows”, and satellite sensors are tuned to measure in these windows.


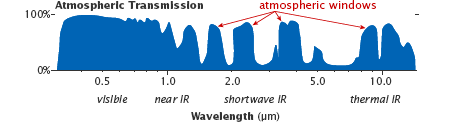
Atmospheric Windows

Consider a satellite with one of the highest spatial resolutions - WorldView-3(Spatial resolution is a value characterizing the size of the smallest objects distinguishable in the image; nadir is the direction that coincides with the direction of gravity at a given point).

Characteristics of the shooting equipment WorldView-3

Spectral range	Name	Range, nm	Spatial resolution in nadir, m
Panchromatic (1 channel; covers the visible part of the spectrum)		450-800	0.31
Multispectral (8 channels)	Coastal	400-450	1.24
	Blue	450-510
	Green	510-580
	Yellow	585-625
	Red	630-690
	Red edge	705-745
	Near infrared	770-895
	Near infrared	860-1040
Multi-band Short Infrared (8 channels)	SWIR-1	1195-1225	3.70
	SWIR-2	1550-1590
	SWIR-3	1640-1680
	SWIR-4	1710-1750
	SWIR-5	2145-2185
	SWIR-6	2185-2225
	SWIR-7	2235-2285
	SWIR-8	2295-2365

In addition to these channels, WorldView-3 also has 12 channels specifically designed for atmospheric correction - CAVIS (Clouds, Aerosols, Vapors, Ice, and Snow) with a resolution of 30 m in nadir and wavelengths from 0.4 to 2.2 microns.


Example shot from WorldView-2; panchromatic channel


Example of images with different spatial resolutions

Other interesting satellites are SkySat-1 and its twin SkySat-2. They are interesting in that they can shoot videos lasting up to 90 seconds over one territory with a frequency of 30 frames / sec and a spatial resolution of 1.1 m.


Video recording from SkySat satellites The

spatial resolution of the panchromatic channel is 0.9 m, the multispectral channels (blue, green, red, near infrared) are 2 m.

Some more examples:

1. The PlanetScope satellite constellation performs a survey with a spatial resolution of 3 m in red, green, blue and near infrared;
   
2. A group of satellites RapidEye performs a survey with a spatial resolution of 5 m in red, extreme red, green, blue and near infrared;
   
3. A series of Russian satellites “Resource-P” performs imaging with a spatial resolution of 0.7-1 m in the panchromatic channel, 3-4 m in multispectral channels (8 channels).
   

Hyperspectral sensors, in contrast to multispectral ones, divide the spectrum into many narrow ranges (approximately 100-200 channels) and have a spatial resolution of a different order: 10-80 m.

Hyperspectral images are not as widespread as multispectral images. There are few spacecraft on board which hyperspectral sensors are installed. Among them are Hyperion aboard NASA EO-1 satellite (decommissioned), CHRIS aboard PROBA satellite, owned by the European Space Agency, FTHSI aboard MightySatII satellite, US Air Force Research Laboratory, GAW (hyperspectral equipment) on Russian spacecraft “ Resource-P ".


Processed hyperspectral image from the on-board sensor CASI 1500; up to 228 channels; spectral range 0.4 - 1 nm


The processed image from the EO-1 space sensor; 220 channels; spectral range 0.4 - 2.5 nm

To simplify the work with multi-channel images, libraries of pure materials exist . They show the reflectivity of pure materials.

Image pre-processing

Before proceeding to the analysis of images, it is necessary to perform their preliminary processing:

1. Georeferencing;
   
2. Orthocorrection;
   
3. Radiometric correction and calibration;
   
4. Atmospheric correction.
   

Suppliers of satellite imagery take additional measurements to pre-process the images, and can give out both processed images and raw ones with additional information for self-correction.

It is also worth mentioning the color correction of satellite images - bringing the image in natural colors (red, green, blue) to a more familiar view for a person.

The approximate geolocation is calculated by the initial position of the satellite in orbit and the image geometry. Geo-referencing is refined by Ground Control Points (GCP). These control points are searched on the map and in the image, and knowing their coordinates in different coordinate systems, you can find the transformation parameters (conformal, affine, perspective or polynomial) from one coordinate system to another. GCP search is performed using GPS shooting [ source. 1 sec 230, source 2 ] or by comparing two images, on one of which the GCP coordinates are exactly known, by key points .

Ortho image correction is a process of geometric image correction, which eliminates perspective distortions, turns, distortions caused by lens distortion and others. The image is then reduced to a planned projection, that is, one in which each point of the terrain is observed strictly vertically, in nadir.

Since satellites are shooting from a very high altitude (hundreds of kilometers), then when shooting in a nadir, distortions should be minimal. But the spacecraft cannot shoot all the time in nadir, otherwise it would have to wait a very long time for the moment when it passes over a given point. To eliminate this drawback, the satellite is “turned over", and most of the frames are promising. It should be noted that shooting angles can reach 45 degrees, and at high altitude this leads to significant distortion.

Orthocorrection should be carried out if measuring and positional properties of the image are needed, because image quality will deteriorate due to additional operations. It is performed by reconstructing the geometry of the sensor at the time of registration for each image line and representing the relief in raster form.

Модель камеры спутника представляется в виде обобщенных аппроксимирующих функций (рациональных полиномов — RPC коэффициентов), а высотные данные могут быть получены в результате наземных измерений, при помощи горизонталей с топографической карты, стереосъемки, по радарным данным или из общедоступных грубых цифровых моделей рельефа: SRTM (разрешение 30-90 м) и ASTER GDEM (разрешение (15-90 м).

Радиометрическая коррекция — исправление на этапе предварительной подготовки снимков аппаратных радиометрических искажений, обусловленных характеристиками используемого съемочного прибора.

For scanner filming devices, such defects are observed visually as image modulation (vertical and horizontal stripes). Radiometric correction also removes image defects observed as bad pixel images.


Removing bad pixels and vertical stripes

Radiometric correction is performed by two methods:

1. Using known parameters and settings of the survey instrument (correction tables);
   
2. Statistically.
   

In the first case, the necessary correction parameters are determined for the survey instrument based on lengthy ground and flight tests. Correction by a statistical method is performed by identifying a defect and its characteristics directly from the image itself to be corrected.

Radiometric calibration of images - the translation of "raw values" of brightness in physical units, which can be compared with the data of other images:

$$

Where $$ - energy brightness for the spectral zone $$;
$$ - raw brightness values;
$$ - calibration factor;
$$Is the calibration constant.

The electromagnetic radiation of the satellite, before it is detected by the sensor, will pass through the Earth’s atmosphere twice. There are two main effects of the influence of the atmosphere - scattering and absorption. Scattering occurs when gas particles and molecules in the atmosphere interact with electromagnetic radiation, deflecting it from the original path. During absorption, part of the radiation energy is converted into the internal energy of the absorbing molecules, as a result of which the atmosphere is heated. The effect of scattering and absorption on electromagnetic radiation changes with the transition from one part of the spectrum to another.


Factors affecting reflected solar radiation incident on satellite sensors

There are various algorithms for performing atmospheric correction (e.g.DOS method - Dark Object Subtraction ). The input parameters for the models are: the geometry of the location of the Sun and the sensor, the atmospheric model for gaseous components, the aerosol model (type and concentration), the optical thickness of the atmosphere, the surface reflection coefficient, and spectral channels.
For atmospheric correction, you can also apply the algorithm for removing haze from the image - Single Image Haze Removal Using Dark Channel Prior ( implementation ).


Case Study Single Image Haze Removal Using Dark Channel Prior

Index images

When studying objects from multichannel images, it is often not absolute values ​​that are important, but the characteristic relations between the brightness values ​​of the object in different spectral zones. To do this, build the so-called index images. In such images, the desired objects stand out more clearly and in contrast to the original image.

Index Image Examples

Index Name	Formula	Application
Iron Oxide Index	Red Blue	To detect iron oxides
Clay Minerals Index	Ratio of luminance values ​​within the mid-infrared channel (CIR). CIK1 / CIK2, where CIK1 is a range from 1.55 to 1.75 microns, CIK2 is a range from 2.08 to 2.35 microns	To detect clay minerals
Iron Mineral Index	The ratio of the brightness value in the average infrared (SIK1; from 1.55 to 1.75 μm) channel to the brightness value in the near infrared channel (NIR). SIK1 / BIK	To detect the content of ferruginous minerals
Red Color Index (RI)	Based on the difference in reflectivity of red-colored minerals in the red (K) and green (H) ranges. RI = (K - 3) / (K + 3)	To detect iron oxide in the soil
Normalized Differential Snow Index (NDSI)	NDSI is a relative value characterized by the difference in reflectivity of snow in the red (K) and short-wave infrared (KIK) ranges. NDSI = (K - KIK) / (K + KIK)	It is used to highlight areas covered with snow. For snow NDSI> 0.4
Water Index (WI)	WI = 0.90 μm / 0.97 μm	It is used to determine the water content in vegetation from hyperspectral images.
Normalized Differential Vegetation Index (NDVI)	Chlorophyll of plant leaves reflects radiation in the near infrared (NIR) range of the electromagnetic spectrum and absorbs in red (K). The ratio of brightness values ​​in these two channels allows you to clearly separate and analyze vegetable from other natural objects. NDVI = (NIR - K) / (NIR + K)	Shows the presence and condition of vegetation. NDVI values ​​range from -1 to 1; Dense vegetation: 0.7; Sparse vegetation: 0.5; Open soil: 0.025; Clouds: 0; Snow and ice: -0.05; Water: -0.25; Artificial materials (concrete, asphalt): -0.5

Working with satellite imagery in Python

One of the formats in which it is customary to store satellite images is GeoTiff (we confine ourselves to it). To work with GeoTiff in Python, you can use the gdal or rasterio library .

To install gdal and rasterio, it is better to use conda:

conda install -c conda-forge gdal
conda install -c conda-forge rasterio

Other satellite imagery libraries are easily installed via pip.

Reading GeoTiff via gdal:

from osgeo import gdal
import numpy as np
src_ds = gdal.Open('image.tif')
img = src_ds.ReadAsArray()
#height, width, band
img = np.rollaxis(img, 0, 3)
width = src_ds.RasterXSize
height = src_ds.RasterYSize
gt = src_ds.GetGeoTransform()
#геокоординаты крайних точек снимка
minx = gt[0]
miny = gt[3] + width*gt[4] + height*gt[5] 
maxx = gt[0] + width*gt[1] + height*gt[2]
maxy = gt[3]

There are a lot of coordinate systems for satellite images. They can be divided into two groups: geographical coordinate systems (GCS) and flat coordinate systems (GCS).

In GSK, the units of measurement are angular and coordinates are represented in decimal degrees. The most famous HSC is WGS 84 (EPSG: 4326).

In UCS, the units are linear and the coordinates can be expressed as meters, feet, kilometers, etc., so they can be linearly interpolated. For the transition from GSK to PSK, cartographic projections are used. One of the most famous projections is the Mercator projection.

It is customary to store a map (markup of a picture) not in a raster form, but in the form of points, lines and polygons. The geo-coordinates of the vertices of these geometric objects are stored inside the files with the markup of images. You can use fiona and shapely libraries to read and work with them.

Script for rasterizing polygons:

import numpy as np
import rasterio
#fiona умеет работать с разными форматами хранения полигонов, например shp и geojson
import fiona
import cv2
from shapely.geometry import shape
from shapely.ops import cascaded_union
from shapely.ops import transform
from shapely.geometry import MultiPolygon
def rasterize_polygons(img_mask, polygons):
    if not polygons:
        return img_mask
    if polygons.geom_type == 'Polygon':
        polygons = MultiPolygon([polygons])
    int_coords = lambda x: np.array(x).round().astype(np.int32)
    exteriors = [int_coords(poly.exterior.coords) for poly in polygons]
    interiors = [int_coords(pi.coords) for poly in polygons
                 for pi in poly.interiors]
    cv2.fillPoly(img_mask, exteriors, 255)
    cv2.fillPoly(img_mask, interiors, 0)
    return img_mask
def get_polygons(shapefile):
    geoms = [feature["geometry"] for feature in shapefile]
    polygons = list()
    for g in geoms:
            s = shape(g)
            if s.geom_type == 'Polygon':
                if s.is_valid:
                    polygons.append(s)
                else:
                    #устраняем самопересечения полигона
                    polygons.append(s.buffer(0))
            elif s.geom_type == 'MultiPolygon':
                for p in s:
                    if p.is_valid:
                        polygons.append(p)
                    else:
                        #устраняем самопересечения полигона
                        polygons.append(p.buffer(0))
    mpolygon = cascaded_union(polygons)
    return mpolygon
#читаем снимок и geojson файл с полигонами
src = rasterio.open('image.tif')
shapefile = fiona.open('buildings.geojson', "r")
#геокоординаты снимка (системы координат снимка и полигонов должны совпадать)
left = src.bounds.left
right = src.bounds.right
bottom = src.bounds.bottom
top = src.bounds.top
height,width = src.shape
#извлекаем мультиполигоны
mpolygon = get_polygons(shapefile)
#так как система координат плоская, то можем получить координаты полигонов уже на самом изображении
mpolygon = transform(lambda x, y, z=None: (width * (x - left) / float(right - left),\
                                                       height - height * (y - bottom) / float(top - bottom)), mpolygon)
#рисуем маску
real_mask = np.zeros((height,width), np.uint8)
real_mask = rasterize_polygons(real_mask, mpolygon)

During decryption of images, the operation of crossing polygons may be necessary (for example, automatically marking buildings on the map, you also want to automatically remove the markup of buildings in those places of the image where there are clouds). There is a Wyler-Atherton algorithm for this, but it only works with polygons without self-intersections. To eliminate self-intersections, you need to check the intersection of all edges with other edges of the polygon and add new vertices. These vertices will break the corresponding edges into pieces. The shapely library has a method for eliminating self-intersections - buffer (0).

To transfer from GSK to UCS, you can use the PyProj library (or do it in rasterio):

#переводим координаты из географической системы координат epsg:4326 в координаты плоской системы координат epsg:32637 (ПСК для Москвы) 
def wgs84_to_32637(lon, lat):
    from pyproj import Proj, transform
    inProj = Proj(init='epsg:4326')
    outProj = Proj(init='epsg:32637')
    x,y = transform(inProj,outProj,lon,lat)
    return x,y

Principal Component Method

If the image contains more than three spectral channels, you can create a color image of the three main components, thereby reducing the amount of data without noticeable loss of information.

Such a transformation is also carried out for a series of images taken at different times, brought into a single coordinate system, to identify the dynamics, which is clearly manifested in one or two components.

Script to compress 4-channel image to 3-channel:

from osgeo import gdal
from sklearn.decomposition import IncrementalPCA
from sklearn import preprocessing
import numpy as np
import matplotlib.pyplot as plt
#читаем снимок, меняем порядок на height, width, band и вырезаем часть изображения, чтобы PCA быстрее справился с данными
src_ds = gdal.Open('0.tif')
img = src_ds.ReadAsArray()
img = np.rollaxis(img, 0, 3)[300:1000, 700:1700, :]
height, width, bands = img.shape
#готовим данные для PCA
data = img.reshape((height * width, 4)).astype(np.float)
num_data, dim = data.shape
pca = IncrementalPCA(n_components = 3, whiten = True)
#cтандартизация данных (достаточно и центрирования)
x = preprocessing.scale(data)
#сжимаем каналы и приводим к виду удобному для визуализации
y = pca.fit_transform(x)
y = y.reshape((height, width, 3))
#нормализуем яркость пикселей
for idx in range(0, 3):
    band_max = y[:, :, idx].max()
    y[:, :, idx] = np.around(y[:, :, idx] * 255.0 / band_max).astype(np.uint8)

Image from the PlanetScope satellite group (red, green, blue without color correction)


Image from the PlanetScope satellite group (green, red, near infrared)


Image obtained using the main component method

Spectral Unmixing Method

The spectral separation method is used to recognize objects in images that are much smaller than the pixel size.

The essence of the method is as follows: mixed spectra are analyzed by comparing them with known pure spectra, for example, from the already mentioned spectral libraries of pure materials. A quantitative assessment of the ratio of this known (clean) spectrum and impurities in the spectrum of each pixel occurs. After performing such an assessment, an image painted so that the color of the pixel will mean which component prevails in the spectrum of this pixel can be obtained.


Mixed spectral curve


Decrypted image

Satellite imagery segmentation

At the moment, state-of-the-art results in binary image segmentation tasks show modifications to the U-Net model .


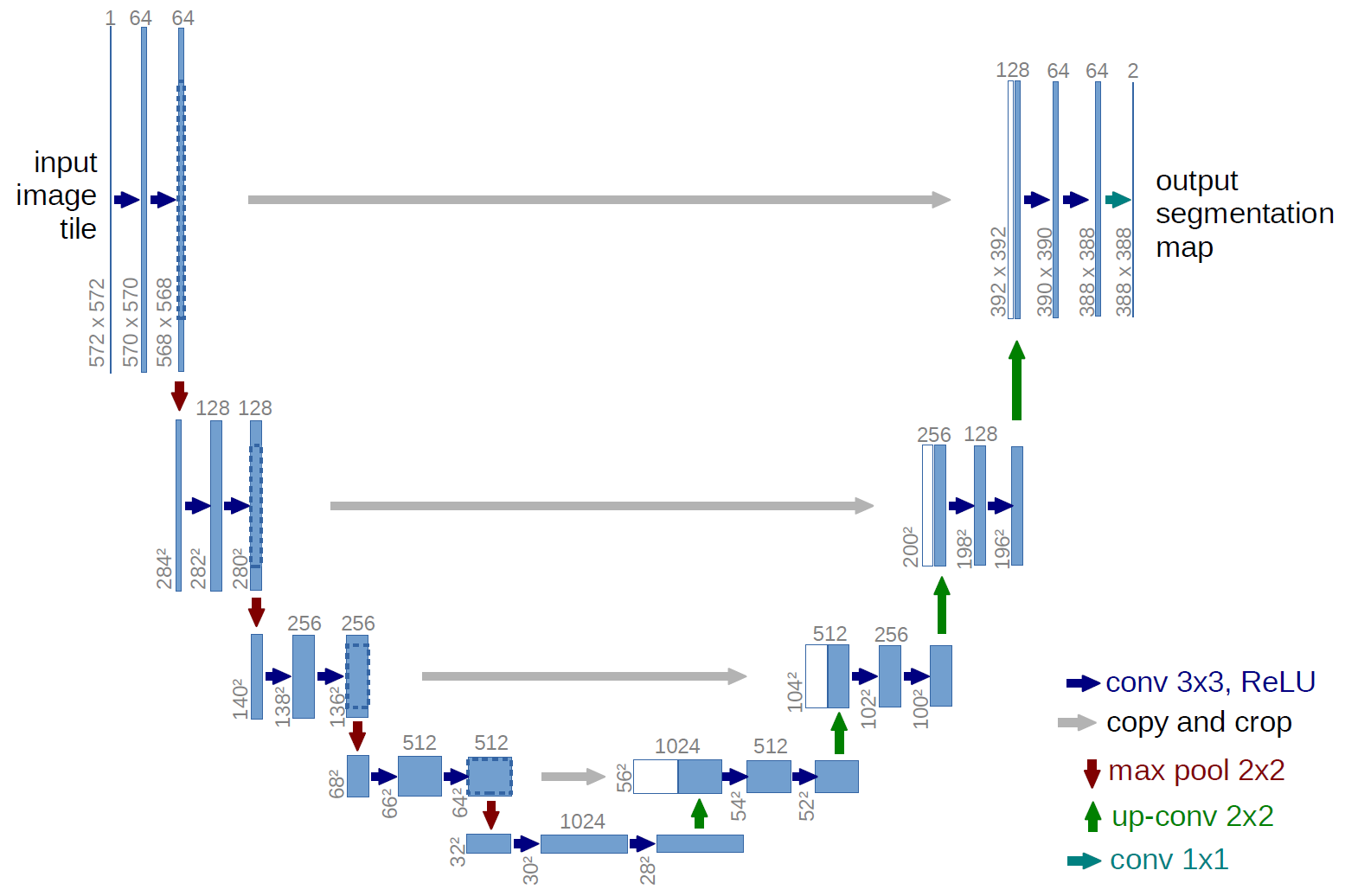
The architecture of the U-Net model (the size of the output image is smaller than the size of the input image; this is done because the network predicts worse at the edges of the image)

The author of U-Net developed an architecture based on another model - Fully convolutional network (FCN), the feature of which is the presence of convolutional words (not counting max-pooling).
U-Net differs from FCN in that layers are added in which max-pooling is replaced by up-convolution. Thus, new layers gradually increase the output resolution. Also, signs from the encoder part are combined with signs from the decoder part, so that the model can make more accurate predictions due to additional information.

The model, in which there is no feature forwarding from the encoder part to the decoder part, is called SegNet and in practice shows worse results than U-Net.


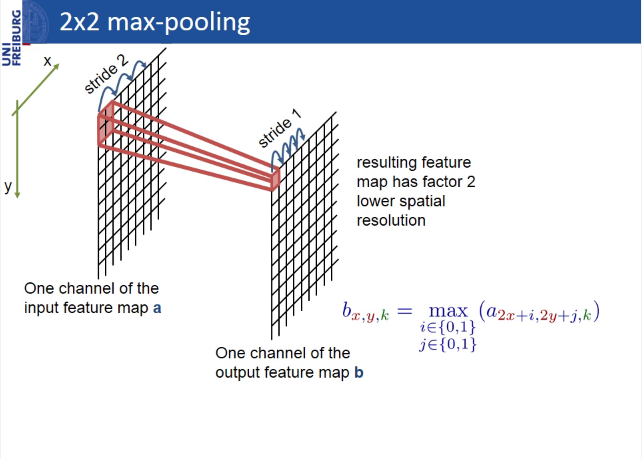
Max-pooling


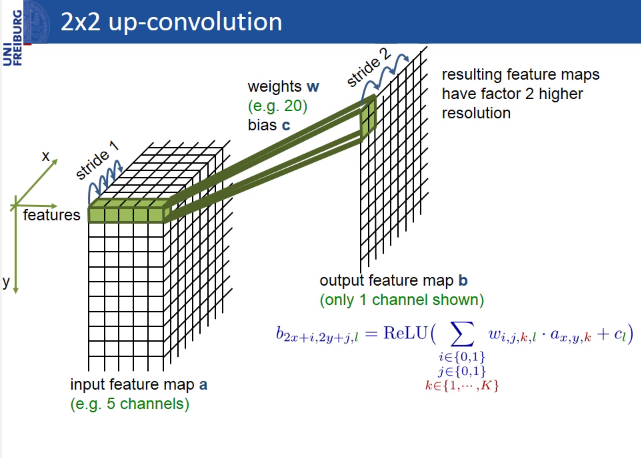
Up-convolution

The absence of layers in the U-Net, Segnet and FCN, which are tied to the size of the image, allows you to submit images of different sizes to the input of the same network (the image size must be a multiple of the number of filters in the first convolution layer).

In keras, this is implemented as follows:

inputs = Input((channel_number, None, None))

Learning, like prediction, can be done either on image fragments (crop), or on the entire image, if the GPU memory allows. Moreover, in the first case:
1) the size of the batches is larger, which will have a good effect on the accuracy of the model if the data is noisy and heterogeneous;
2) less risk of retraining, as there is much more data than when training on full-size images.

However, when training on crop, the edge effect is more pronounced - the network predicts less accurately at the edges of the image than in areas closer to the center (the closer the prediction point to the border, the less information about what is next). The problem can be solved by predicting the mask on fragments with overlapping and discarding or averaging the areas on the border.

U-Net is a simple and powerful architecture for the task of binary segmentation, on github you can find more than one implementation for any DL framework, but for segmenting a large number of classes this architecture loses to other architectures, for example, PSP-Net. Here you can read an interesting overview of architectures for semantic image segmentation.

Building height determination

The height of buildings can be determined by their shadows. To do this, you need to know: pixel size in meters, shadow length in pixels, and sun (solar) elevation angle (angle of the sun above the horizon).


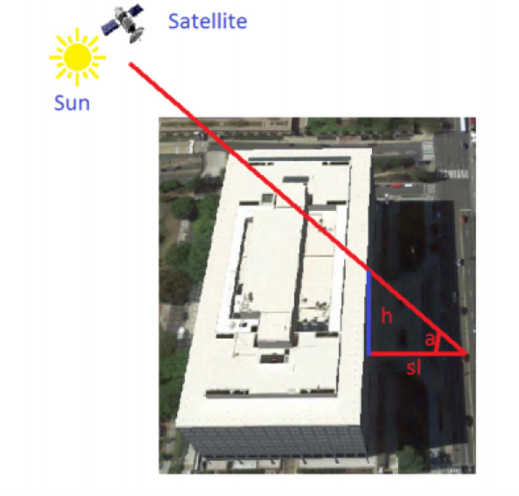
The geometry of the sun, satellite and building

The whole difficulty of the task is to segment the shadow of the building as accurately as possible and determine the length of the shadow in pixels. The presence of clouds in the pictures also adds to the problems.

There are more accurate methods for determining the height of the building. For example, you can take into account the angle of the satellite above the horizon.



An example of the algorithm for determining the height of buildings by shadow

In the images from the PlanetScope satellite group with a spatial resolution of 3 m, the error in determining the height of buildings by MAPE (mean absolute percentage error) was ~ 30%. In total, 40 buildings and one shot were examined. However, in submeter images, the researchers received an error of only 4-5% .

Conclusion

Remote sensing of the Earth provides many opportunities for analytics. For example, companies such as Orbital Insight, Spaceknow, Remote Sensing Metrics, OmniEarth and DataKind, based on satellite imagery, monitor production and consumption in the United States, analyze urbanization, traffic, vegetation, economics, etc. At the same time, the pictures themselves are becoming more accessible. For example, images from the Landsat-8 and Sentinel-2 satellites with a spatial resolution of more than 10 m are in the public domain and are constantly updated.

In Russia, Sovzond, ScanEx, Racurs, Geo-Alliance and the Northern Geographic Company also conduct geoanalysis using satellite images and are official distributors of remote sensing satellite operator companies: Russian Space Systems (Russia), DigitalGlobe (USA), Planet (USA) ), Airbus Defense and Space (France-Germany) and others.

PS Yesterday we launched an online competition on satellite imagery , consisting of two tasks:

1. Segmentation of buildings and cars and counting cars;
   
2. Determination of the heights of buildings.
   

So everyone who is interested in the field of computer vision and remote sensing of the Earth, join us!

We plan to hold another competition for the pictures of Roscosmos, Airbus Defense and Space and PlanetScope.