Barnes-Hut t-SNE and LargeVis: Large Data Visualization
With data sets of millions of copies in machine learning problems, you will not surprise anyone long ago. However, few people wonder how to qualitatively visualize these titanic layers of information. When the size of the dataset exceeds a million, it becomes rather sad to use standard t-SNE; it remains to be played with downsampling or completely limited to crude statistical tools. But for each task there is a tool. In my article, I would like to consider two algorithms that overcome the barrier of quadratic complexity: the already well-known Barnes-Hut t-SNE and the new contender for the title of “golden hammer infovis'a” LargeVis.

(This is not a picture of an abstract artist, but a bird's eye view of a LiveJournal dataset)
Although t-SNE is about ten years old, one can safely say that it has already been tested by time. It is popular not only among seasoned adherents of data science, but also among authors of popular science articles . About him already wrote on Habré; Also about this visualization algorithm, there are many good articles on the Internet.
However, almost all of these articles talk about standard t-SNE. Let me remind him briefly:
Where - Kullback-Leibler divergence.
Intuitively for the three-dimensional case, this can be represented as follows. You havebilliard balls. You label them and hang them by the thread from the ceiling. Threads of different sizes, so now in the three-dimensional space of your room hangs a dataset from elements with . You connect each pair of balls with an ideal spring so that the springs are exactly the length you need (not sag, but not stretched). The stiffness of the springs is selected as follows: if there are no other balls next to a ball, all springs are more or less weak. If exactly one ball is a neighbor, and all the others are far away, then this neighbor will have a very stiff spring, and all the others will have a weak spring. If there are two neighbors, there will be stiff springs to the neighbors (but weaker than in the previous case), and to all the others - even weaker. And so on.
Now you take the resulting design and try to place it on the table. Even if a three-dimensional object consists of freely moving nodes, in general it cannot be placed on a plane (imagine how you are holding a tetrahedron to a table), so you simply position it so that the tension or tension of the springs is as small as possible. Do not forget to make a correction for the fact that in a two-dimensional space each ball will have fewer nearest neighbors, but more neighbors at an average distance (remember the cube-square law). Most springs are so weak that they can not be taken into account at all, but elements connected by strong springs are best placed side by side. You move in small steps, moving from an arbitrary initial configuration, slowly reducing the tension of the springs.The better you can restore the original tension of the springs from their current tension, the better.
(they forgot for a second that we know that the initial tension of the springs is zero)
(did I mention that these are magic balls and springs that pass through each other?)
(why bother with such nonsense? - left as an exercise for the reader)
So , modern data science packages do not really implement this. Standard t-SNE has complexity. As a result of recent studies , it turned out that this is redundant, and almost the same result can be achieved inoperations.
First, consider everything in the first stepseems obviously redundant. Most of them will still be zero. Limit this number: find the k nearest neighbors of each data instance, and calculatehonestly only for them; for the rest we put zero. Accordingly, we will consider the sum in the denominator of the corresponding formula only for these elements. The question arises: how exactly to choose this number of neighbors? The answer to it is surprisingly simple: we already have a parameter responsible for the relationship between the global and local structure of the algorithm -, perplexity! Its characteristic values range from 5 to 50, and the more the dataset, the more perplexity. Just what you need. Using the VP tree, you can find a sufficient number of neighbors pertime. If we continue the analogy with the springs, this is not how to connect all the balls in pairs, but for each ball, hang the springs up to, say, its five nearest neighbors.
Secondly…
Let's digress a bit to discuss Barnes-Hut. About this algorithm there was no separate article on Habré, and here just an excellent occasion to tell about it.
Probably, everyone knows the classical gravitational problem of N bodies: from given masses and initial coordinates of N cosmic bodies and the well-known law of their interaction, construct functions that show the coordinates of objects at all subsequent time instants. Its solution is not expressed through the usual algebraic functions, but can only be found numerically, for example, using the Runge-Kutta method . Unfortunately, such numerical methods for solving differential equations have complexity, and even on modern computers are not well considered when the number of objects exceeds .
For simulations with such a huge number of bodies, some simplifications have to be made. Note that for a triple of bodies A, B, and C, the sum of the forces acting on A from the sides B and C is equal to the force exerted by a single body (BC), placed at the point of the center of mass of B and C. This alone is not enough for optimization, therefore, we apply one more trick. We break the space into cells. If the distance from the body A to the cell is large and there is more than one body in the cell, we will assume that an object with a total mass of objects inside is placed exactly in the center of this cell. Its position will deviate slightly from the real center of mass of the cell contents, but the further the cell, the more insignificant the error in the angle of action of the force will be.
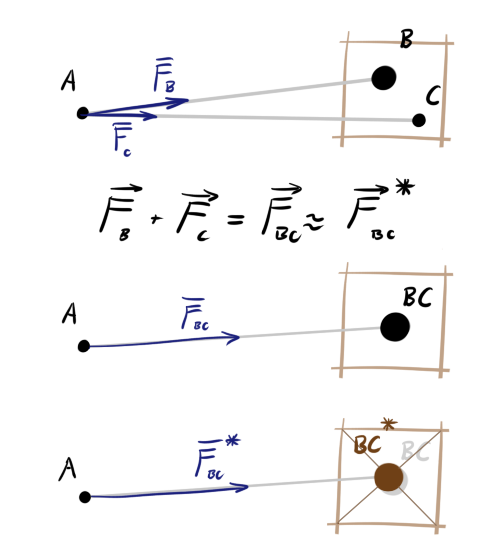
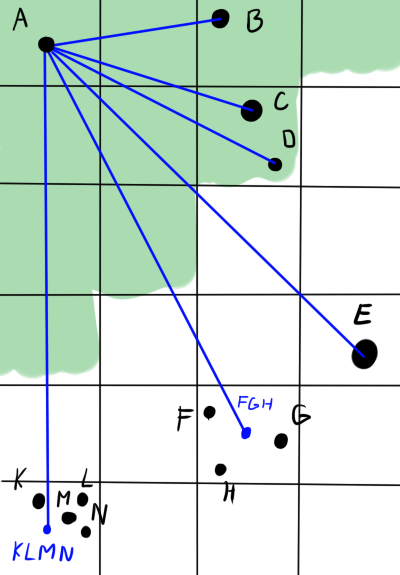
In the picture below, green indicates the area of proximity of body A. Blue indicates the direction of action of the forces. The bodies B, C, and D exert force on A separately. Although C and D are in the same cell, they are in the area of accuracy. E also exerts power alone - it is one in the cell. But the objects F, G and H are far enough from A and close enough to each other that the interaction can be brought closer. The center of the cell will not always coincide well with the actual position of the center of gravity (see K, L, M, N), but on average, with a large distance and a large number of bodies, the error will be negligible.
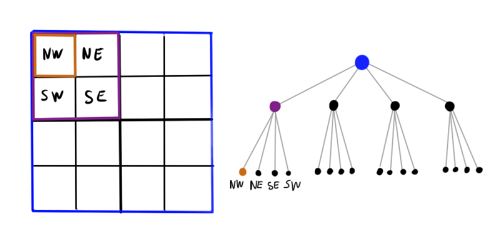
It became better: we reduced the effective number of objects by several times. But how to choose the optimal partition size? If the partition is too small, there will be no sense in it, and if it is too large, the error will increase and you will have to put a very large distance at which we will be ready to sacrifice accuracy. Let's take a step forward: instead of a grid with a fixed step, we divide the plane rectangle into a hierarchy of cells. Large cells contain small ones, even smaller ones, and so on. The resulting data structure is a tree, where each non-leaf node spawns four child nodes. This design is called a quadtree.) For the three-dimensional case, respectively, the octotree is used. Now, when calculating the force acting on a certain body, it is possible to go around the tree until a cell with a sufficient level of fineness meets, and then use the approximation.
Nodes into which not a single object falls make sense to be farther on, therefore this structure is not as heavy as it might seem at first glance. On the other hand, there is definitely an overhead, so I would say that while there are fewer than 100 simulated objects, such a cunning data structure can be slightly harmful (depending on implementation).
Now more formally:
Algorithm 1:
Let - the distance from the body to the center of the cell in question, Is the side of this cell - a predefined threshold for fineness. To determine the force exerted on an object, go around the quad tree, starting from the root.
Here's a more detailed implementation of the algorithm in steps. Beautiful Barnes-Hut animation of a galaxy simulation. Various Barnes-Hut implementations can be found on the github.
Obviously, such an interesting idea could not go unnoticed in other areas of science. Barnes-Hut is used wherever there are systems with a large number of objects, each of which acts on others according to a simple law that does not change much in space: swarm simulation, computer games. So data analysis was also no exception. Let us describe in more detail the step of gradient descent (3) in t-SNE:
Where attracting forces are indicated - repulsive, and Is the normalizing factor. Thanks to previous optimization considered to be but - yet . This is where the quad-tree trick and Barens-Hut described above will come in handy, but instead of Newton’s law,. This simplification allows us to calculate behind average. The disadvantage is obvious: errors due to discretization of space. Laurens van der Maaten in the article above claims that it is not even clear whether they are limited at all (links to relevant articles are provided). Be that as it may, the results obtained using the Barens-Hut t-SNE with normally selectedlook consistent and consistent. You can usually put or and forget about him.
Is it even faster? Yes . Why stop at the point-to-cell approximation, when you can simplify the situation even further: if two cells are far enough apart, you can approximate not only the final, but also the initial one (“cell-cell” approximation). This is called the dual-tree algorithm (there is no Russian name yet). We do not start the recursion above for each instance of the data, but begin to bypass the quad tree and when fineness reaches the desired value, we bypass the same quad tree and apply the total force from the second round cell to each instance inside the selected cell of the first round. This approach allows you to squeeze a little more speed, but the error begins to accumulate much faster, and you have to set a smaller. Yes, and such a detour is implemented not so much where.
Good, but can it be even faster? Jian Tang and company, answer yes!
Once we have sacrificed accuracy, why not sacrifice thevirgin determinism as well. We will use random algorithms to get the result fortime. First, instead of searching for the nearest neighbors using the vantage point tree, we use random projection trees (RT-trees). Secondly, instead of honestly calculating the gradient with simplifications through Barnes-Hut, we will simply sample the terms in the negative part.
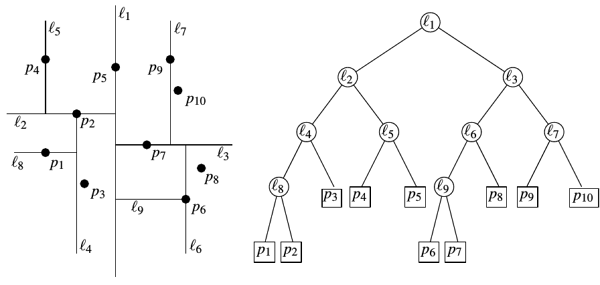
The idea of splitting a plane using a quad tree was not bad. Now let's try to break the plane into sectors using something simpler. How about a kd tree ?
Algorithm 2:
Parameters: - minimum size -
MakeTree dataset ()
Somehow too primitive. The perpendicularity of the partition plane of some coordinate axis looks suspicious. There is a more advanced version: random projection trees (RT-trees). We will recursively divide the space, each time choosing a random unit vector, the plane will go perpendicular to it. For slight asymmetry of the tree, we also add a little noise to the anchor point of the plane.
Algorithm 3:
ChooseRule (X) // Meta-function that returns the predicate by which we will divide the space
MakeRPTree ()
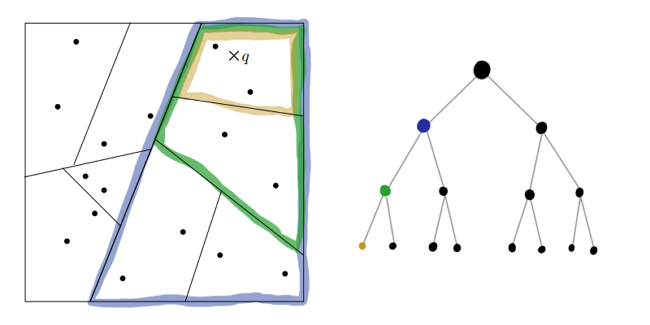
Is such a rough and chaotic partition capable of yielding at least some results? It turns out that yes! In the case when the multidimensional data actually lies near a not very multidimensional hyper-folding, the RT-trees behave quite decent (see the proofs on the first link and here ). Even when the data do have an effective dimension comparable to, knowledge about projections carries a lot of information.
Hmm, complexity: calculating the median is still and we do it on each of steps. We simplify the choice of the hyperplane even more: we will generally abandon the anchor point. At each step of the recursion, we simply select two random points from the nextand draw a plane equally spaced from them.
It seems that we threw out from the algorithm everything that at least somehow reminds of mathematical rigor or accuracy. How can the resulting trees help us with finding the nearest neighbors? Obviously, the neighbors of the data points on the graph sheet are the first candidates in its kNN. But this is not accurate: if the point lies next to the hyperplane of the partition, the real neighbors may appear in a completely different sheet. The resulting approximation can be improved if you build several RP-trees. The intersection of the sheets of the resulting graphs for each is a much better area to search.
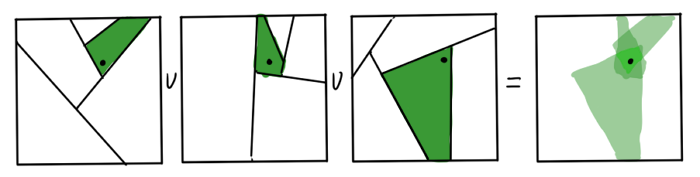
Trees do not need too much, it undermines the speed. The resulting approximation is brought to mind using the heuristic "my neighbor’s neighbor is most likely my neighbor." It is argued that quite a few iterations are enough to get a decent result.
The authors of the article assure that the effective implementation of all this works for time. There is, however, one thing that they don’t mention: O-big swallows a giant constant that is affected, the number of RP-trees, and the number of stages of heuristic tuning.
After calculating the kNN, Jian Tang and KO calculate the similarity of data in the source space using the same formula as in t-SNE.
Please note that the amount in the denominator is considered only by kNN, the rest equal to 0; also.
After that, a cunning theoretical maneuver is proposed: now we look at the received, as on the weight of the edges of some graph, where the nodes are the elements . We encode the information on the weights of this graph using the setin display space. Let the probability of observing a binary unweighted edge is equal to
The t distribution is used again, only in a slightly different way; still remember about a different number of neighbors in different layers in spaces with different. The probability that the source graph had an edge with weight in:
Multiply the probabilities for all edges and get the location maximum likelihood method:
Where - the set of all pairs that are not in the list of nearest neighbors, and - a hyperparameter showing the influence of nonexistent edges. Logarithm:
Again they received a sum consisting of two parts: one attracts each other close to each other the other repels , which were not neighbors of each other, they only look different. We also got the problem again that the exact calculation of the second sum will take, since there are a lot of missing arcs in our graph. This time, instead of using a quad tree, it is proposed to sample the nodes of the graph to which there are no arcs. This trick came from machine word processing. There for faster understanding of the context for each wordthat stands in the text next to the word , do not take all the words from the dictionary that are next to do not occur, but only a few arbitrary words, with a probability proportional to 3/4 of the degree of their frequency (the 3/4 indicator is selected empirically, more details here ). We are for each nodeto which there is an edge from with weight in , we will sample several arbitrary nodes up to which there are no edges, in proportion to 3/4 of the degree of the number of arcs emanating from those nodes.
Where Is the number of negative edges per node, and .
Becausecan vary within a fairly wide range, to stabilize the gradient, an advanced version of the sampling technique should be used. Instead of sorting out with the same frequency, we take them with a probability proportional to and pretend that the edge is singular.
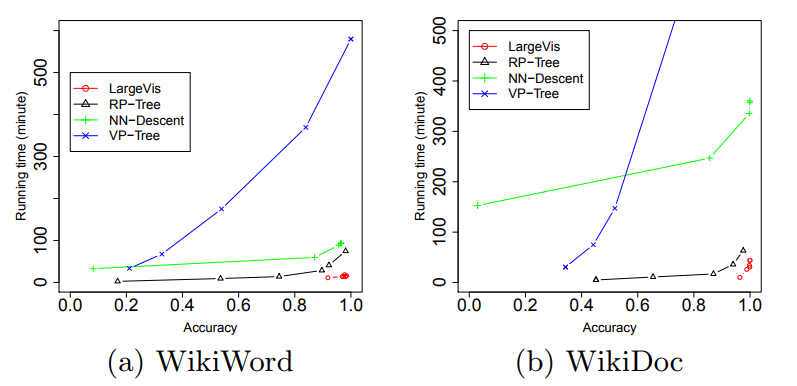
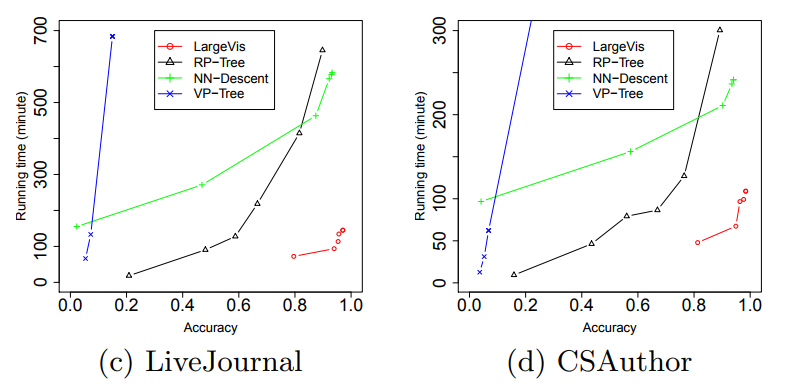
Wow What do all these tricks give us? Approximately five-fold increase in speed on moderately large datasets compared to the Barnes-Hut t-SNE!

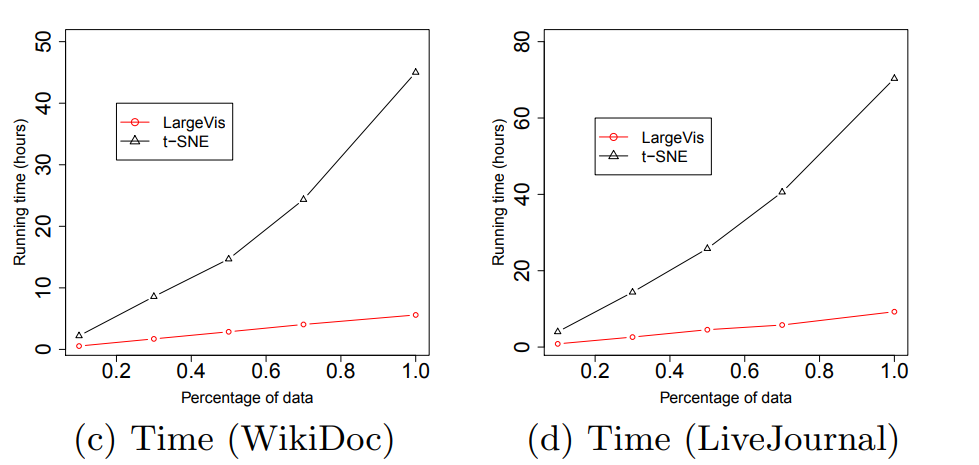
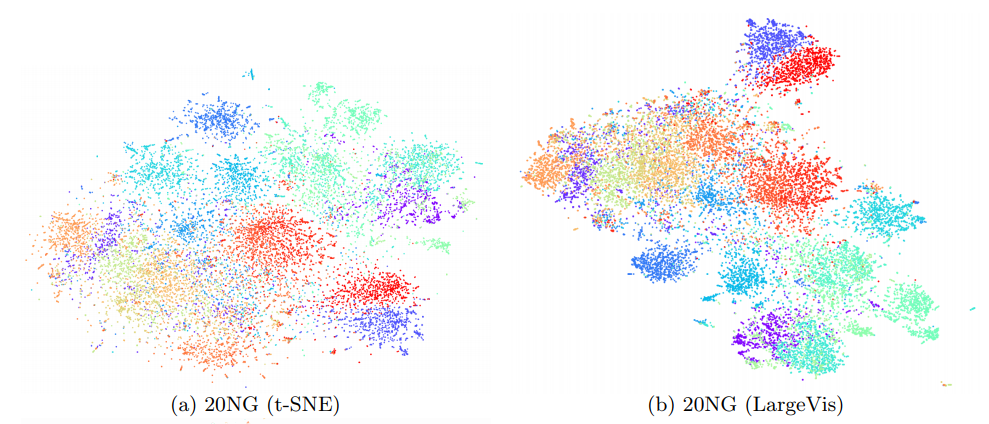


(Pictures taken from the article )
At the same time, the quality of visualization is about the same. An attentive reader will notice that on the relatively small dataset of 20 Newsgroups () LargeVis loses t-SNE. This is the influence of the insidious constant, which remained behind the scenes. Students, remember, the thoughtless use of algorithms with a lesser degree under O-large is harmful to your health!
Finally, a couple of practical points. There is an official implementation of LargeVis, but in my opinion the code there is a little ugly, use at your own risk. The number of negative samples per nodeusually taken equal to 5 (came from machine word processing). The experiments showed a very slight increase in quality with increasingfrom 3 to 7. The number of trees should be taken the larger, the larger the data set, but not too much. Focus on the minimum value of 10 for and close to excess 100 . the creators of the algorithm are equal to 7, without explaining why. Most important: LargeVis parallels perfectly at all stages of work. Due to the sparseness of the weight matrix, asynchronous sparse gradient descent on different flows is unlikely to hit each other.
Thanks for attention. I hope that now it’s become clearer to you what kind of mysterious method = 'barnes_hut' and angle are in the parameters of sklearn's TSNE, and you won’t be lost when you need to visualize a dataset of ten million records. If you work with a lot of data, maybe you will find your own application of Barens-Hut or decide to implement LargeVis. Just in case, here are brief notes on the work of the latter. Have a nice day!


(This is not a picture of an abstract artist, but a bird's eye view of a LiveJournal dataset)
t-SNE with modifications
Although t-SNE is about ten years old, one can safely say that it has already been tested by time. It is popular not only among seasoned adherents of data science, but also among authors of popular science articles . About him already wrote on Habré; Also about this visualization algorithm, there are many good articles on the Internet.
However, almost all of these articles talk about standard t-SNE. Let me remind him briefly:
- Count for each pair a pair of data points x i , x j ∈ X their similarity to each other in the original space using the Gaussian kernel:
p j | i = exp ( - ‖ x i - x j ‖ 2 / ( 2 σ 2 i )∑ k ≠ i ( exp ( - ‖ x i - x k ‖ / ( 2 σ 2 i ) )
p i j = p j | i + p i | j2
- For each pair of display points, express their similarity in the visualization space using the t-distribution kernel
- Build an objective function and minimize it relative using gradient descent
Where - Kullback-Leibler divergence.
Intuitively for the three-dimensional case, this can be represented as follows. You havebilliard balls. You label them and hang them by the thread from the ceiling. Threads of different sizes, so now in the three-dimensional space of your room hangs a dataset from elements with . You connect each pair of balls with an ideal spring so that the springs are exactly the length you need (not sag, but not stretched). The stiffness of the springs is selected as follows: if there are no other balls next to a ball, all springs are more or less weak. If exactly one ball is a neighbor, and all the others are far away, then this neighbor will have a very stiff spring, and all the others will have a weak spring. If there are two neighbors, there will be stiff springs to the neighbors (but weaker than in the previous case), and to all the others - even weaker. And so on.
Now you take the resulting design and try to place it on the table. Even if a three-dimensional object consists of freely moving nodes, in general it cannot be placed on a plane (imagine how you are holding a tetrahedron to a table), so you simply position it so that the tension or tension of the springs is as small as possible. Do not forget to make a correction for the fact that in a two-dimensional space each ball will have fewer nearest neighbors, but more neighbors at an average distance (remember the cube-square law). Most springs are so weak that they can not be taken into account at all, but elements connected by strong springs are best placed side by side. You move in small steps, moving from an arbitrary initial configuration, slowly reducing the tension of the springs.The better you can restore the original tension of the springs from their current tension, the better.
(they forgot for a second that we know that the initial tension of the springs is zero)
(did I mention that these are magic balls and springs that pass through each other?)
(why bother with such nonsense? - left as an exercise for the reader)
So , modern data science packages do not really implement this. Standard t-SNE has complexity. As a result of recent studies , it turned out that this is redundant, and almost the same result can be achieved inoperations.
First, consider everything in the first stepseems obviously redundant. Most of them will still be zero. Limit this number: find the k nearest neighbors of each data instance, and calculatehonestly only for them; for the rest we put zero. Accordingly, we will consider the sum in the denominator of the corresponding formula only for these elements. The question arises: how exactly to choose this number of neighbors? The answer to it is surprisingly simple: we already have a parameter responsible for the relationship between the global and local structure of the algorithm -, perplexity! Its characteristic values range from 5 to 50, and the more the dataset, the more perplexity. Just what you need. Using the VP tree, you can find a sufficient number of neighbors pertime. If we continue the analogy with the springs, this is not how to connect all the balls in pairs, but for each ball, hang the springs up to, say, its five nearest neighbors.
Secondly…
Barnes-Hut Algorithm
Let's digress a bit to discuss Barnes-Hut. About this algorithm there was no separate article on Habré, and here just an excellent occasion to tell about it.
Probably, everyone knows the classical gravitational problem of N bodies: from given masses and initial coordinates of N cosmic bodies and the well-known law of their interaction, construct functions that show the coordinates of objects at all subsequent time instants. Its solution is not expressed through the usual algebraic functions, but can only be found numerically, for example, using the Runge-Kutta method . Unfortunately, such numerical methods for solving differential equations have complexity, and even on modern computers are not well considered when the number of objects exceeds .
For simulations with such a huge number of bodies, some simplifications have to be made. Note that for a triple of bodies A, B, and C, the sum of the forces acting on A from the sides B and C is equal to the force exerted by a single body (BC), placed at the point of the center of mass of B and C. This alone is not enough for optimization, therefore, we apply one more trick. We break the space into cells. If the distance from the body A to the cell is large and there is more than one body in the cell, we will assume that an object with a total mass of objects inside is placed exactly in the center of this cell. Its position will deviate slightly from the real center of mass of the cell contents, but the further the cell, the more insignificant the error in the angle of action of the force will be.

In the picture below, green indicates the area of proximity of body A. Blue indicates the direction of action of the forces. The bodies B, C, and D exert force on A separately. Although C and D are in the same cell, they are in the area of accuracy. E also exerts power alone - it is one in the cell. But the objects F, G and H are far enough from A and close enough to each other that the interaction can be brought closer. The center of the cell will not always coincide well with the actual position of the center of gravity (see K, L, M, N), but on average, with a large distance and a large number of bodies, the error will be negligible.

It became better: we reduced the effective number of objects by several times. But how to choose the optimal partition size? If the partition is too small, there will be no sense in it, and if it is too large, the error will increase and you will have to put a very large distance at which we will be ready to sacrifice accuracy. Let's take a step forward: instead of a grid with a fixed step, we divide the plane rectangle into a hierarchy of cells. Large cells contain small ones, even smaller ones, and so on. The resulting data structure is a tree, where each non-leaf node spawns four child nodes. This design is called a quadtree.) For the three-dimensional case, respectively, the octotree is used. Now, when calculating the force acting on a certain body, it is possible to go around the tree until a cell with a sufficient level of fineness meets, and then use the approximation.

Nodes into which not a single object falls make sense to be farther on, therefore this structure is not as heavy as it might seem at first glance. On the other hand, there is definitely an overhead, so I would say that while there are fewer than 100 simulated objects, such a cunning data structure can be slightly harmful (depending on implementation).
Now more formally:
Algorithm 1:
Let - the distance from the body to the center of the cell in question, Is the side of this cell - a predefined threshold for fineness. To determine the force exerted on an object, go around the quad tree, starting from the root.
- If there are no elements in the current cell, skip it
- Otherwise, if there is only one element in the node and it is not , directly add its effect to the total strength
- Otherwise, if , we consider this node as a single whole object, and add its total strength, as described above
- Otherwise, we recursively run this procedure for all daughter cells of the current cell.
Here's a more detailed implementation of the algorithm in steps. Beautiful Barnes-Hut animation of a galaxy simulation. Various Barnes-Hut implementations can be found on the github.
Obviously, such an interesting idea could not go unnoticed in other areas of science. Barnes-Hut is used wherever there are systems with a large number of objects, each of which acts on others according to a simple law that does not change much in space: swarm simulation, computer games. So data analysis was also no exception. Let us describe in more detail the step of gradient descent (3) in t-SNE:
Where attracting forces are indicated - repulsive, and Is the normalizing factor. Thanks to previous optimization considered to be but - yet . This is where the quad-tree trick and Barens-Hut described above will come in handy, but instead of Newton’s law,. This simplification allows us to calculate behind average. The disadvantage is obvious: errors due to discretization of space. Laurens van der Maaten in the article above claims that it is not even clear whether they are limited at all (links to relevant articles are provided). Be that as it may, the results obtained using the Barens-Hut t-SNE with normally selectedlook consistent and consistent. You can usually put or and forget about him.
Is it even faster? Yes . Why stop at the point-to-cell approximation, when you can simplify the situation even further: if two cells are far enough apart, you can approximate not only the final, but also the initial one (“cell-cell” approximation). This is called the dual-tree algorithm (there is no Russian name yet). We do not start the recursion above for each instance of the data, but begin to bypass the quad tree and when fineness reaches the desired value, we bypass the same quad tree and apply the total force from the second round cell to each instance inside the selected cell of the first round. This approach allows you to squeeze a little more speed, but the error begins to accumulate much faster, and you have to set a smaller. Yes, and such a detour is implemented not so much where.
LargeVis
Good, but can it be even faster? Jian Tang and company, answer yes!
Once we have sacrificed accuracy, why not sacrifice the
RT trees
The idea of splitting a plane using a quad tree was not bad. Now let's try to break the plane into sectors using something simpler. How about a kd tree ?
Algorithm 2:
Parameters: - minimum size -
MakeTree dataset ()
- If a return current like a leaf node
- Otherwise
- Randomly select a variable number
- Rule (x): = median () // Predicate splitting the data subspace with a hyperplane perpendicular to the coordinate axis and passing through the median of values this element variable .
- LeftTree: = MakeTree ({x X: Rule (x) = true})
- RightTree: = MakeTree ({x X: Rule (x) = false})
- Return [Rule, LeftTree, RightTree]

Somehow too primitive. The perpendicularity of the partition plane of some coordinate axis looks suspicious. There is a more advanced version: random projection trees (RT-trees). We will recursively divide the space, each time choosing a random unit vector, the plane will go perpendicular to it. For slight asymmetry of the tree, we also add a little noise to the anchor point of the plane.
Algorithm 3:
ChooseRule (X) // Meta-function that returns the predicate by which we will divide the space
- Select a random unit vector from
- Choose random
- Let be - the farthest data point from it in
- : = random number in
- Return Rule (x): = (median () + )
MakeRPTree ()
- If a return current like a leaf node
- Otherwise
- Rule (x): = ChooseRule (X)
- LeftTree: = MakeTree ({x X: Rule (x) = true})
- RightTree: = MakeTree ({x X: Rule (x) = false})
- Return [Rule, LeftTree, RightTree]

Is such a rough and chaotic partition capable of yielding at least some results? It turns out that yes! In the case when the multidimensional data actually lies near a not very multidimensional hyper-folding, the RT-trees behave quite decent (see the proofs on the first link and here ). Even when the data do have an effective dimension comparable to, knowledge about projections carries a lot of information.
Hmm, complexity: calculating the median is still and we do it on each of steps. We simplify the choice of the hyperplane even more: we will generally abandon the anchor point. At each step of the recursion, we simply select two random points from the nextand draw a plane equally spaced from them.
It seems that we threw out from the algorithm everything that at least somehow reminds of mathematical rigor or accuracy. How can the resulting trees help us with finding the nearest neighbors? Obviously, the neighbors of the data points on the graph sheet are the first candidates in its kNN. But this is not accurate: if the point lies next to the hyperplane of the partition, the real neighbors may appear in a completely different sheet. The resulting approximation can be improved if you build several RP-trees. The intersection of the sheets of the resulting graphs for each is a much better area to search.

Trees do not need too much, it undermines the speed. The resulting approximation is brought to mind using the heuristic "my neighbor’s neighbor is most likely my neighbor." It is argued that quite a few iterations are enough to get a decent result.


The authors of the article assure that the effective implementation of all this works for time. There is, however, one thing that they don’t mention: O-big swallows a giant constant that is affected, the number of RP-trees, and the number of stages of heuristic tuning.
Sampling
After calculating the kNN, Jian Tang and KO calculate the similarity of data in the source space using the same formula as in t-SNE.
Please note that the amount in the denominator is considered only by kNN, the rest equal to 0; also.
After that, a cunning theoretical maneuver is proposed: now we look at the received, as on the weight of the edges of some graph, where the nodes are the elements . We encode the information on the weights of this graph using the setin display space. Let the probability of observing a binary unweighted edge is equal to
The t distribution is used again, only in a slightly different way; still remember about a different number of neighbors in different layers in spaces with different. The probability that the source graph had an edge with weight in:
Multiply the probabilities for all edges and get the location maximum likelihood method:
Where - the set of all pairs that are not in the list of nearest neighbors, and - a hyperparameter showing the influence of nonexistent edges. Logarithm:
Again they received a sum consisting of two parts: one attracts each other close to each other the other repels , which were not neighbors of each other, they only look different. We also got the problem again that the exact calculation of the second sum will take, since there are a lot of missing arcs in our graph. This time, instead of using a quad tree, it is proposed to sample the nodes of the graph to which there are no arcs. This trick came from machine word processing. There for faster understanding of the context for each wordthat stands in the text next to the word , do not take all the words from the dictionary that are next to do not occur, but only a few arbitrary words, with a probability proportional to 3/4 of the degree of their frequency (the 3/4 indicator is selected empirically, more details here ). We are for each nodeto which there is an edge from with weight in , we will sample several arbitrary nodes up to which there are no edges, in proportion to 3/4 of the degree of the number of arcs emanating from those nodes.
Where Is the number of negative edges per node, and .
Becausecan vary within a fairly wide range, to stabilize the gradient, an advanced version of the sampling technique should be used. Instead of sorting out with the same frequency, we take them with a probability proportional to and pretend that the edge is singular.
Wow What do all these tricks give us? Approximately five-fold increase in speed on moderately large datasets compared to the Barnes-Hut t-SNE!





(Pictures taken from the article )
At the same time, the quality of visualization is about the same. An attentive reader will notice that on the relatively small dataset of 20 Newsgroups () LargeVis loses t-SNE. This is the influence of the insidious constant, which remained behind the scenes. Students, remember, the thoughtless use of algorithms with a lesser degree under O-large is harmful to your health!
Finally, a couple of practical points. There is an official implementation of LargeVis, but in my opinion the code there is a little ugly, use at your own risk. The number of negative samples per nodeusually taken equal to 5 (came from machine word processing). The experiments showed a very slight increase in quality with increasingfrom 3 to 7. The number of trees should be taken the larger, the larger the data set, but not too much. Focus on the minimum value of 10 for and close to excess 100 . the creators of the algorithm are equal to 7, without explaining why. Most important: LargeVis parallels perfectly at all stages of work. Due to the sparseness of the weight matrix, asynchronous sparse gradient descent on different flows is unlikely to hit each other.
Conclusion
Thanks for attention. I hope that now it’s become clearer to you what kind of mysterious method = 'barnes_hut' and angle are in the parameters of sklearn's TSNE, and you won’t be lost when you need to visualize a dataset of ten million records. If you work with a lot of data, maybe you will find your own application of Barens-Hut or decide to implement LargeVis. Just in case, here are brief notes on the work of the latter. Have a nice day!

