Advanced Minesweeper Tactics
- Transfer
[Friday's translation of a 1999 article by one of the authors of the Thief game engine, Sean Barrett]
In this position, I know that there are a lot of mines around me, but I can’t determine where they are. Several mines can be in one of two places (pink or blue), a group of mines can be located in one of two combinations (light / dark green). In addition, there is still a difficult situation with "5" and "6" in the upper left corner, which I did not highlight in any way.

Blue / pink - mutually exclusive pairs, light / dark green - mutually exclusive groups
Minesweeper can be played in two ways: as a logical or probabilistic game.
Technically, probability implies logic. If you can logically prove that the mine should be in a certain place, then the probability is 100%. If you can prove that she is not in this place, then the probability is 0%. That is, in a sense, only probabilities are important to us. However, the player uses logical deduction to recognize such absolute situations. Sometimes, especially at low levels of difficulty, it is enough to pass the level, no calculation of probabilities is required.
But there are situations when the whole logic of the world cannot save you. A simple example is the situation with “T”, which is visible in the bottom center. It is a little complicated by additional adjacent mines. (In the simplest case, “2” is replaced by “1” and “5” by “3” so that the situation is symmetrical.)
There is noa way to get more information about the probable position of one mine left in one of these cells. Chances are fifty to fifty - you can throw a coin. When you get something like this, it’s best to immediately make a choice and not put it off for later. If the guess is wrong, then you will at least save time on solving the rest of the field. (But personally, I strive for completeness, so I leave such cases for later. And do not blame yourself for not guessing. When a win or loss depends on a coin toss - this is a bad game design.)
In the endgame you can use a very simple tactic - count the number of remaining mines. Suppose I decided everything except the bottom right of the field. There can be only two configurations of mines corresponding to the data:

Possible configurations minutes in the lower right corner
if you was such a position counter and says that there are only two mines, the answer is ready: it must be configured Bed and .
If the counter said that there were three mines, it is not necessarily the configuration A . This could be Scheme B with the remaining mine in one of the lower right groups of 3x3 cells.
In fact, the odds are in favor of the configuration of Bed and .
If you examine probabilities only “locally”, you see that each of the cells in the marked mutually exclusive groups has a 50-50 chance of being a mine. Speaking “locally”, I mean that if there is “1” next to two unknown cells, then the probability of a hidden mine for each of them is 50%.
It is this situation that developed in the bottom center: each of the neighboring cells adjacent to an unknown pair contains exactly one mine, that is, each of the neighboring data fragments assumes a 50 percent probability. In the upper left corner a similar situation:
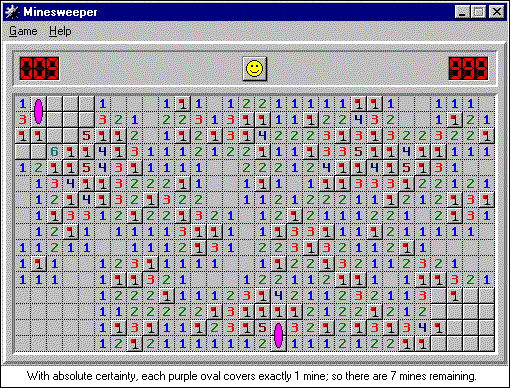
With absolute accuracy, each of the pink ovals has one mine, that is, only 7 minutes remain.
The situation in the lower right corner is also somewhat similar: next to each of the numbers on the “border” there is one mine and two cells in which it can to be.
If next to the cell there is one hidden mine, but three closed cells, then the probability of a mine in each of the cells is 33%; each of the four closed cells has a 25% chance. If we have two hidden mines and three closed cells, then each cell has a 66% probability.
Here is the “local probability” situation for the entire field:
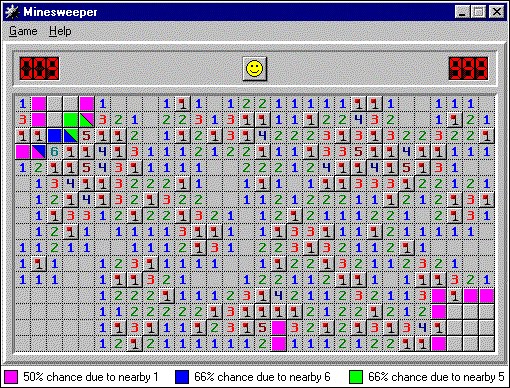
As you can see, several cells in the upper left region have several probabilities; closed cell next to "2" and "6" and one next to "3" and "5". (The cell next to “5” and “6” thanks to them still has a probability of 66%, so there is no visible discrepancy.)
You are probably wondering what the existence of conflicting local probabilities means. Intuition may suggest that the most likely to win. For example, a cell between “6” and “2” should actually have 66%. This will mean that in the leftmost cell with a probability of 50%, it is actually equal to 33%. Or you can try to somehow combine priorities: perhaps the probability will be 5/6 or an average value.
But none of this is actually true. The data from which the probabilities are derived are notare independent of each other, therefore, no straightforward mathematical calculations will be correct. The reason for the local guess at about 50% down in the center is that it is truly independent of nothing else. If we randomly recreate the field according to the data already available to us, then exactly in half of the models the mines will be in one of two cells. (Probability sometimes confuses people who cannot figure out which rules for calculating probabilities are applicable in a particular situation. This approach is a guaranteed way to go, because it is based on determining probability in statistical forecasting: the calculation is performed by measurement in all possible configurations that could lead to the current situation, all of which are considered equally probable.)
That is, for correct measurements in the situation in the upper left corner, you need to consider all possible mine configurations that satisfy the already collected data, and then calculate what percentage of them contains the mine in the desired position.
Direct counting would take a lot of time. Fortunately, there are other ways.
An abstract method of calculating probabilities is to bypass all possible mine configurations, discard configurations that do not meet the collected data, and calculate statistics for each of the possible positions.
A more practical approach is to consider only those options that cannot be discarded. To do this, we need to apply logic and generate all possible situations that may correspond to the available data. I already showed two options for the lower right corner, but the probabilities for the upper left:
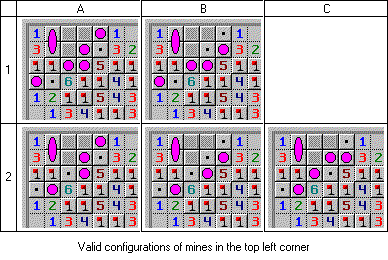
Possible configurations for the upper left corner
(As before, an oval with a height of two cells shows that the mine can equally likely be in any of the cells. I could list each of these two cases separately, that is, 10 configurations would turn out, but no There is no use for us for this. Table structure: two rows (numbered as “1” and “2”) differ in the position of the mines in the fourth row. Three columns are characterized by the position of the mines in the second row.)
Now there is the temptation to exclaim: “yeah, here are five cases, so that we can calculate the number of cases for each of the possible positions of the mine.” For example, a mine is in the fourth row (next to the bottom left “1”) is on the left in the two upper cases, and on the right in the three lower cases. Therefore, it can be decided that it has a 60% probability of being on the right, next to “6”. (This is a position with conflicting local probabilities of 50% and 66%.)
However, we miss one subtlety - the number of mines is different in some cases: in A1, six mines, in B2 - four, and five in all other cases.
For a detailed study of this subtlety, let's return to a simpler situation in the lower right corner.

Possible configurations with the lower right corner
Suppose that I have already opened the rest of the field and know that there are exactly three mines left.
It is tempting to suggest that configuration A with exactly three mines is most likely . But this is not true.
Another temptation is to remember how many mines there were and how many cells there were, and say: "what are the chances that the lower 3x3 region will be empty." This is also not true. It is very difficult to explain why this is a mistake, probably, it can be compared with the Monty Hall paradox . However, suffice it to say that in reality the chances in this situation do not depend on the total number of mines and the size of the field.
The correct answer is: how many possible configurations of three mines correspond to our knowledge of the field? From the figure we see that the two: the configuration A and Bed and . But in B there are only two mines. The third mine can be in any of the cells of the lower 3x3 region, about which we have not yet collected any data. That is, there are nine configuration options for B in total , I just did not portray them all.
Therefore, there are only ten possible configurations. Each of the ten configurations is equally probable. (As I mentioned earlier, this is critical for understanding the probability. The chances that the computer generated any of these options are small, but they are equally small because the computer [as far as we know] gaveeach configuration has equal chances. You are equally likely to throw out a configuration of ten “eagles” in a row and a sequence of two “eagles”, one “tails”, one “eagle”, three “tails”, one “eagle”, one “tails” and one “eagle” . It is more likely to throw five “eagles” and five “tails” in total, but not a specific sequence of “eagles” and “tails”. In Minesweeper, we are dealing with mine configurations that are similar to coin toss sequences.)
Since each of ten configurations (nine for B , one for A ) is equally probable, configuration B in this case has a 90% probability!
If at this stage there were four mines, then configuration A would have nine options. Configuration B would have one option for each arrangement of two mines in the lower left corner; this is C (9.2) , that is, 9! / ((9-2)! * 2!) or 9 * 8/2, equal to 36. In this case, configuration B would have a probability of only 75%.
With five mines, configuration A would have 36 options, and configuration B would have 9 * 8 * 7/6 = 84 options; that is, the odds of B would be a little over 66%.
In the case of six minutes, B would have a 60% probability. With seven mines, B would have only 50%. With eight mines Bwould be less likely than A; in this case, with so many mines in the remaining positions of the configurations, it becomes smaller. Consider the worst case scenario when 11 minutes remain. (The chance of this is extremely small, but if such a situation arises, then these probabilities apply.) In configuration B , there will be mines in all closed cells, in configuration A in all but one. That is, there are 9 options for A and only one for B.
In our existing field there are nine minutes left. One of them is located in the central lower region, and its position is completely independent, so you can ignore it. That is, we consider the entire field, except for this case: only eight minutes were not found. (In order to avoid confusion, I will continue to explicitly count the oval in the upper left corner, because this is an image of the upper left corner.)
Any combination of the upper left and lower right configurations can be added, except for one of them (A1 + A), for which will take nine minutes. Therefore, we must list each of these possible configurations and count the remaining mines and closed cells.
In fact, the number of closed cells is independent: there are nine in the lower right and three in the upper left, that is, only 12.
Thus, there are a total of 118 possible combinations. Based on this, we can independently calculate the number of combinations for each of the upper left and lower right configurations:
Next, I went around each cell on the field and calculated its probability by summing the number of probabilities in which it appears and dividing by 118. (In fact, simply adding up the above percentages.) In addition, on average, each of the closed cells has mines 15 of 118 options (that is, the chances that at least one closed cell has a mine are very high). [This can be calculated by multiplying the number of remaining mines by closed options, which gives us the average number of mines in closed cells.]

The probabilities of the presence of mines
(It should be said that this does not show all the available information. For example, we know that the probabilities of two dark green cells are associated with 87% - if one is true, then the other too. And the blue 13% cells in which mines of configuration A are also connected. The remaining blue 13 percent cells are not connected. If one of them has mines, the likelihood that any of the remaining ones have mines is reduced.)
Most likely, when playing Minesweeper, you will not want to pore over all these calculations.
And me too.
But I really listed all the possible configurations in the upper left and lower right. I noticed that in one configuration ( B2-B ) one min is used less than in all the others, and I applied the time-tested rule “less min means more open options” (which is valid for as long as the number of closed cells is less than twice the number mines not found). This means that a configuration with fewer mines is much more likely.
Since there were many configurations in the upper left corner, determining the odds for any cell is quite difficult. So I just found out that configuration Bin the lower right corner is much more likely, and accidentally chose one of the suitable cells. (I was hoping that it would allow me to finish the lower right corner, and then, armed with more information about the number of remaining mines, I could complete the upper left corner, after which I would have to drop a coin for selection at the bottom center. Of course, ideally, I had to choose cage that maximizes the probability of obtaining useful information, but any of these conjectures would allow me to "enter" in the lower right corner for further data collection.) The odds were higher in the configuration of Bed and , so I chose the cell in which the mine was in the configuration A .

Eight times out of nine, I would be right.
Unpleasant situation in "Minesweeper"
In this position, I know that there are a lot of mines around me, but I can’t determine where they are. Several mines can be in one of two places (pink or blue), a group of mines can be located in one of two combinations (light / dark green). In addition, there is still a difficult situation with "5" and "6" in the upper left corner, which I did not highlight in any way.

Blue / pink - mutually exclusive pairs, light / dark green - mutually exclusive groups
Minesweeper: logic or probability
Minesweeper can be played in two ways: as a logical or probabilistic game.
Technically, probability implies logic. If you can logically prove that the mine should be in a certain place, then the probability is 100%. If you can prove that she is not in this place, then the probability is 0%. That is, in a sense, only probabilities are important to us. However, the player uses logical deduction to recognize such absolute situations. Sometimes, especially at low levels of difficulty, it is enough to pass the level, no calculation of probabilities is required.
But there are situations when the whole logic of the world cannot save you. A simple example is the situation with “T”, which is visible in the bottom center. It is a little complicated by additional adjacent mines. (In the simplest case, “2” is replaced by “1” and “5” by “3” so that the situation is symmetrical.)
There is noa way to get more information about the probable position of one mine left in one of these cells. Chances are fifty to fifty - you can throw a coin. When you get something like this, it’s best to immediately make a choice and not put it off for later. If the guess is wrong, then you will at least save time on solving the rest of the field. (But personally, I strive for completeness, so I leave such cases for later. And do not blame yourself for not guessing. When a win or loss depends on a coin toss - this is a bad game design.)
Tactics at the end of the game
In the endgame you can use a very simple tactic - count the number of remaining mines. Suppose I decided everything except the bottom right of the field. There can be only two configurations of mines corresponding to the data:

Possible configurations minutes in the lower right corner
if you was such a position counter and says that there are only two mines, the answer is ready: it must be configured Bed and .
If the counter said that there were three mines, it is not necessarily the configuration A . This could be Scheme B with the remaining mine in one of the lower right groups of 3x3 cells.
In fact, the odds are in favor of the configuration of Bed and .
Local probabilities
If you examine probabilities only “locally”, you see that each of the cells in the marked mutually exclusive groups has a 50-50 chance of being a mine. Speaking “locally”, I mean that if there is “1” next to two unknown cells, then the probability of a hidden mine for each of them is 50%.
It is this situation that developed in the bottom center: each of the neighboring cells adjacent to an unknown pair contains exactly one mine, that is, each of the neighboring data fragments assumes a 50 percent probability. In the upper left corner a similar situation:

With absolute accuracy, each of the pink ovals has one mine, that is, only 7 minutes remain.
The situation in the lower right corner is also somewhat similar: next to each of the numbers on the “border” there is one mine and two cells in which it can to be.
If next to the cell there is one hidden mine, but three closed cells, then the probability of a mine in each of the cells is 33%; each of the four closed cells has a 25% chance. If we have two hidden mines and three closed cells, then each cell has a 66% probability.
Here is the “local probability” situation for the entire field:

As you can see, several cells in the upper left region have several probabilities; closed cell next to "2" and "6" and one next to "3" and "5". (The cell next to “5” and “6” thanks to them still has a probability of 66%, so there is no visible discrepancy.)
Local Conflict Resolution
You are probably wondering what the existence of conflicting local probabilities means. Intuition may suggest that the most likely to win. For example, a cell between “6” and “2” should actually have 66%. This will mean that in the leftmost cell with a probability of 50%, it is actually equal to 33%. Or you can try to somehow combine priorities: perhaps the probability will be 5/6 or an average value.
But none of this is actually true. The data from which the probabilities are derived are notare independent of each other, therefore, no straightforward mathematical calculations will be correct. The reason for the local guess at about 50% down in the center is that it is truly independent of nothing else. If we randomly recreate the field according to the data already available to us, then exactly in half of the models the mines will be in one of two cells. (Probability sometimes confuses people who cannot figure out which rules for calculating probabilities are applicable in a particular situation. This approach is a guaranteed way to go, because it is based on determining probability in statistical forecasting: the calculation is performed by measurement in all possible configurations that could lead to the current situation, all of which are considered equally probable.)
That is, for correct measurements in the situation in the upper left corner, you need to consider all possible mine configurations that satisfy the already collected data, and then calculate what percentage of them contains the mine in the desired position.
Direct counting would take a lot of time. Fortunately, there are other ways.
Counting configurations
An abstract method of calculating probabilities is to bypass all possible mine configurations, discard configurations that do not meet the collected data, and calculate statistics for each of the possible positions.
A more practical approach is to consider only those options that cannot be discarded. To do this, we need to apply logic and generate all possible situations that may correspond to the available data. I already showed two options for the lower right corner, but the probabilities for the upper left:

Possible configurations for the upper left corner
(As before, an oval with a height of two cells shows that the mine can equally likely be in any of the cells. I could list each of these two cases separately, that is, 10 configurations would turn out, but no There is no use for us for this. Table structure: two rows (numbered as “1” and “2”) differ in the position of the mines in the fourth row. Three columns are characterized by the position of the mines in the second row.)
Now there is the temptation to exclaim: “yeah, here are five cases, so that we can calculate the number of cases for each of the possible positions of the mine.” For example, a mine is in the fourth row (next to the bottom left “1”) is on the left in the two upper cases, and on the right in the three lower cases. Therefore, it can be decided that it has a 60% probability of being on the right, next to “6”. (This is a position with conflicting local probabilities of 50% and 66%.)
However, we miss one subtlety - the number of mines is different in some cases: in A1, six mines, in B2 - four, and five in all other cases.
Counting mines not found
For a detailed study of this subtlety, let's return to a simpler situation in the lower right corner.

Possible configurations with the lower right corner
Suppose that I have already opened the rest of the field and know that there are exactly three mines left.
It is tempting to suggest that configuration A with exactly three mines is most likely . But this is not true.
Another temptation is to remember how many mines there were and how many cells there were, and say: "what are the chances that the lower 3x3 region will be empty." This is also not true. It is very difficult to explain why this is a mistake, probably, it can be compared with the Monty Hall paradox . However, suffice it to say that in reality the chances in this situation do not depend on the total number of mines and the size of the field.
The correct answer is: how many possible configurations of three mines correspond to our knowledge of the field? From the figure we see that the two: the configuration A and Bed and . But in B there are only two mines. The third mine can be in any of the cells of the lower 3x3 region, about which we have not yet collected any data. That is, there are nine configuration options for B in total , I just did not portray them all.
Therefore, there are only ten possible configurations. Each of the ten configurations is equally probable. (As I mentioned earlier, this is critical for understanding the probability. The chances that the computer generated any of these options are small, but they are equally small because the computer [as far as we know] gaveeach configuration has equal chances. You are equally likely to throw out a configuration of ten “eagles” in a row and a sequence of two “eagles”, one “tails”, one “eagle”, three “tails”, one “eagle”, one “tails” and one “eagle” . It is more likely to throw five “eagles” and five “tails” in total, but not a specific sequence of “eagles” and “tails”. In Minesweeper, we are dealing with mine configurations that are similar to coin toss sequences.)
Since each of ten configurations (nine for B , one for A ) is equally probable, configuration B in this case has a 90% probability!
If at this stage there were four mines, then configuration A would have nine options. Configuration B would have one option for each arrangement of two mines in the lower left corner; this is C (9.2) , that is, 9! / ((9-2)! * 2!) or 9 * 8/2, equal to 36. In this case, configuration B would have a probability of only 75%.
With five mines, configuration A would have 36 options, and configuration B would have 9 * 8 * 7/6 = 84 options; that is, the odds of B would be a little over 66%.
In the case of six minutes, B would have a 60% probability. With seven mines, B would have only 50%. With eight mines Bwould be less likely than A; in this case, with so many mines in the remaining positions of the configurations, it becomes smaller. Consider the worst case scenario when 11 minutes remain. (The chance of this is extremely small, but if such a situation arises, then these probabilities apply.) In configuration B , there will be mines in all closed cells, in configuration A in all but one. That is, there are 9 options for A and only one for B.
Final decision
In our existing field there are nine minutes left. One of them is located in the central lower region, and its position is completely independent, so you can ignore it. That is, we consider the entire field, except for this case: only eight minutes were not found. (In order to avoid confusion, I will continue to explicitly count the oval in the upper left corner, because this is an image of the upper left corner.)
Any combination of the upper left and lower right configurations can be added, except for one of them (A1 + A), for which will take nine minutes. Therefore, we must list each of these possible configurations and count the remaining mines and closed cells.
In fact, the number of closed cells is independent: there are nine in the lower right and three in the upper left, that is, only 12.
| Top left | Bottom right | Number of mines | Min left | Closed options |
|---|---|---|---|---|
| A1 | B | 8 | 0 | 1 |
| B1 | A | 8 | 0 | 1 |
| B1 | B | 7 | 1 | 12 |
| A2 | A | 8 | 0 | 1 |
| A2 | B | 7 | 1 | 12 |
| B2 | A | 7 | 1 | 12 |
| B2 | B | 6 | 2 | 66 |
| C2 | A | 8 | 0 | 1 |
| C2 | B | 7 | 1 | 12 |
Thus, there are a total of 118 possible combinations. Based on this, we can independently calculate the number of combinations for each of the upper left and lower right configurations:
| Configuration | Options | Percent |
|---|---|---|
| A1 | 1 | 1 |
| B1 | thirteen | eleven |
| A2 | thirteen | eleven |
| B2 | 78 | 66 |
| C2 | thirteen | eleven |
| A | fifteen | thirteen |
| B | 103 | 87 |
Next, I went around each cell on the field and calculated its probability by summing the number of probabilities in which it appears and dividing by 118. (In fact, simply adding up the above percentages.) In addition, on average, each of the closed cells has mines 15 of 118 options (that is, the chances that at least one closed cell has a mine are very high). [This can be calculated by multiplying the number of remaining mines by closed options, which gives us the average number of mines in closed cells.]

The probabilities of the presence of mines
(It should be said that this does not show all the available information. For example, we know that the probabilities of two dark green cells are associated with 87% - if one is true, then the other too. And the blue 13% cells in which mines of configuration A are also connected. The remaining blue 13 percent cells are not connected. If one of them has mines, the likelihood that any of the remaining ones have mines is reduced.)
Play the game
Most likely, when playing Minesweeper, you will not want to pore over all these calculations.
And me too.
But I really listed all the possible configurations in the upper left and lower right. I noticed that in one configuration ( B2-B ) one min is used less than in all the others, and I applied the time-tested rule “less min means more open options” (which is valid for as long as the number of closed cells is less than twice the number mines not found). This means that a configuration with fewer mines is much more likely.
Since there were many configurations in the upper left corner, determining the odds for any cell is quite difficult. So I just found out that configuration Bin the lower right corner is much more likely, and accidentally chose one of the suitable cells. (I was hoping that it would allow me to finish the lower right corner, and then, armed with more information about the number of remaining mines, I could complete the upper left corner, after which I would have to drop a coin for selection at the bottom center. Of course, ideally, I had to choose cage that maximizes the probability of obtaining useful information, but any of these conjectures would allow me to "enter" in the lower right corner for further data collection.) The odds were higher in the configuration of Bed and , so I chose the cell in which the mine was in the configuration A .

Eight times out of nine, I would be right.
