Nelder-Mead optimization method. Python implementation example

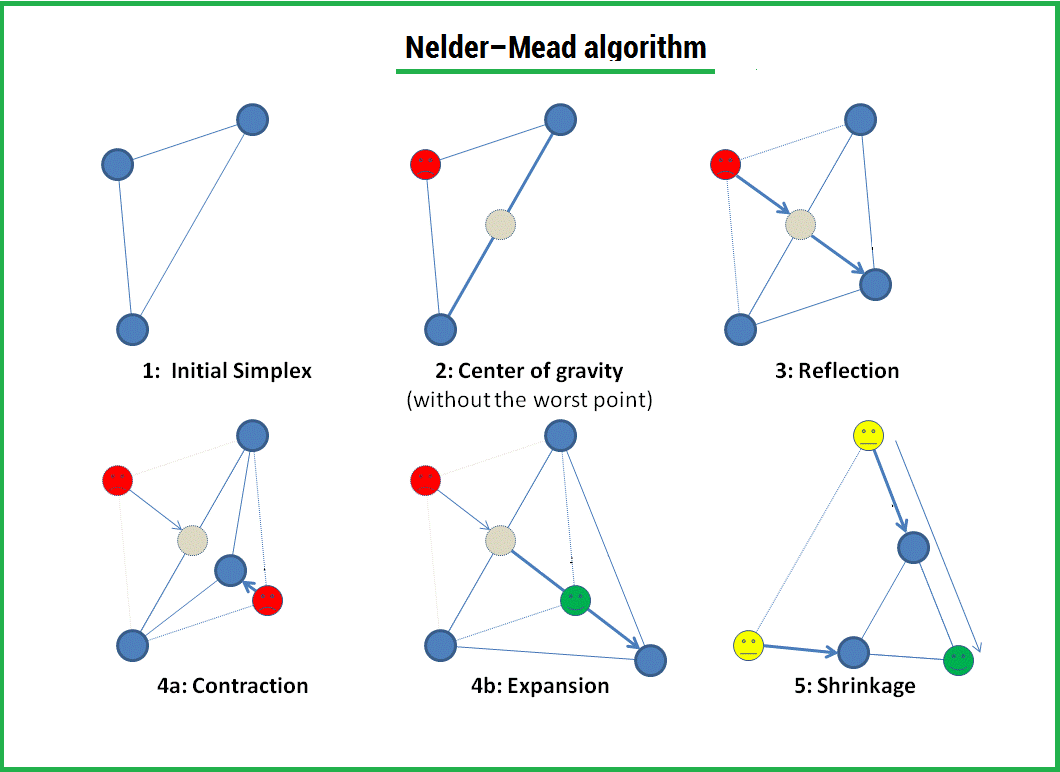
The Nelder-Mead method is a method of optimization (minimum search) of a function of several variables. A simple and at the same time effective method that allows you to optimize functions without using gradients. The method is reliable and, as a rule, shows good results, although there is no theory of convergence. It can be used in the optimize function from the scipy.optimize module of the popular library for the python language, which is used for mathematical calculations.

The algorithm consists in the formation of a simplex ( simplex ) and its subsequent deformation in the direction of the minimum, through three operations:

1) Reflection (reflection);
2) Stretching (expansion);
3) Compression (contract);

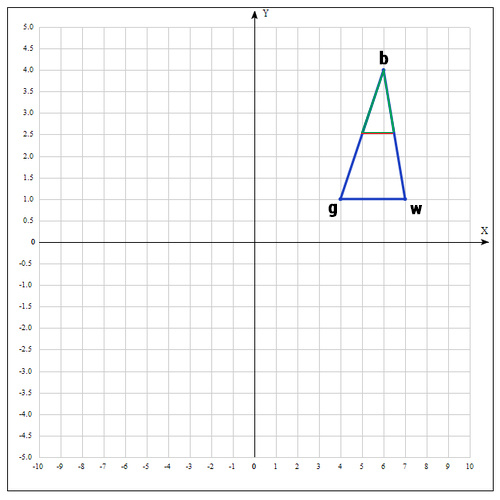
A simplex is a geometric figure, which is an n - dimensional generalization of a triangle. For one-dimensional space, this is a segment; for two-dimensional space, it is a triangle. Thus, an n - dimensional simplex has n + 1 vertices.

Algorithm

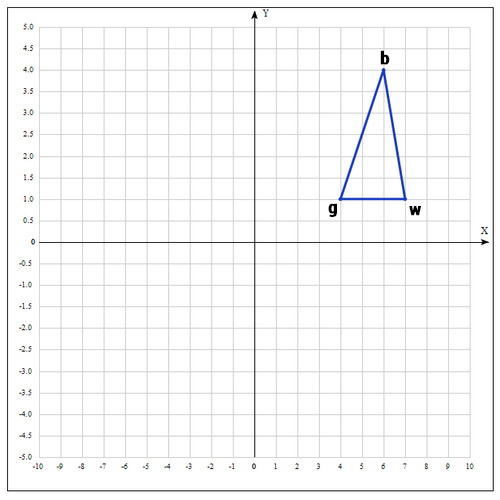
1) Let $$function to be optimized. At the first step, we select three random points (more on this later) and form a simplex (triangle). We calculate the value of the function at each point:$$, $$, $$.

Sort points by function values$$ at these points, thus we obtain the double inequality: $$

We are looking for the minimum of the function, and therefore, at this step, the best point will be that at which the value of the function is minimal. For convenience, we denote the points as follows:

b =$$, g = $$, w = $$where best, good, worst - respectively.



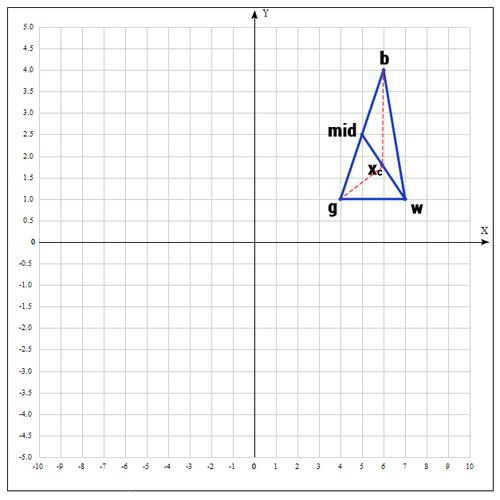
2) At the next step, we find the middle of the segment whose points are g and b. Because the coordinates of the middle of the segment are equal to the half-sum of the coordinates of its ends, we obtain:

$$

In a more general form, you can write this:

$$

3) Apply the reflection operation:
Find the point$$, in the following way:

$$

Those. actually reflect the point w relative to mid. As a rule, they usually take 1. We check our point: if$$then this is a good point. And now we’ll try to increase the distance by 2 times, suddenly we are lucky and we will find the point even better.



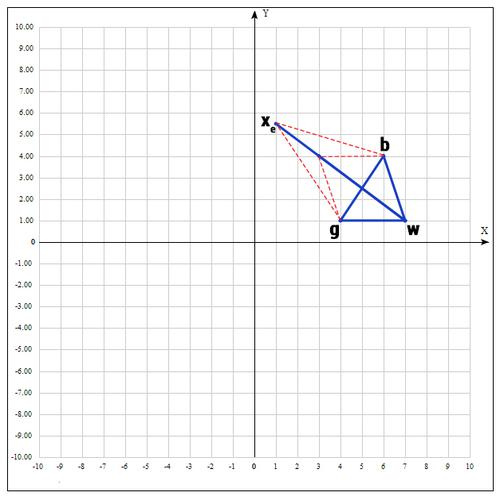
4) Apply the operation of stretching:
Find the point$$ in the following way:

$$

We take γ = 2 as γ, i.e. the distance is increased by 2 times.

Check point$$:

If$$, then we were lucky and we found a point better than it is at the moment, if this did not happen, we would stop at a point $$.

Next, replace the point w with$$, in the end we get:



5) If we were not lucky at all and we did not find good points, we try the compression operation.
As the name of the operation implies, we will reduce our segment and look for good points inside the triangle.

Trying to find a good point$$:

$$

The coefficient β is taken equal to 0.5, i.e. point$$in the middle of the wmid segment.



There is another operation - shrink (reduction). In this case, we redefine the whole simplex. We leave only the "best" point, the rest is defined as follows:

$$

The coefficient δ is taken equal to 0.5.

Essentially move the points towards the current “best” point. The conversion is as follows:



It should be noted that this operation is expensive, since it is necessary to replace points in the simplex. Fortunately, it was found during a large number of experiments that shrink transformation rarely happens in practice.

The algorithm ends when:

1) The required number of iterations was performed.
2) The area of ​​the simplex reached a certain value.
3) The current best solution has reached the required accuracy.

As with most heuristic methods, there is no ideal way to select initializing points. As already mentioned, you can take random points located close to each other to form a simplex; but there is a better solution that is used in the implementation of the algorithm in MATHLAB:

First point selection$$we entrust the user if he has some idea of ​​a possible good solution, otherwise it is randomly selected. The remaining points are selected based on$$, a short distance along the direction of each measurement:

$$

Where $$ Is the unit vector.
$$ defined in this way:
$$ = 0.05 if the coefficient at $$ in the definition $$ not zero.
$$ = 0.00025, if the coefficient at $$ in the definition of zero.

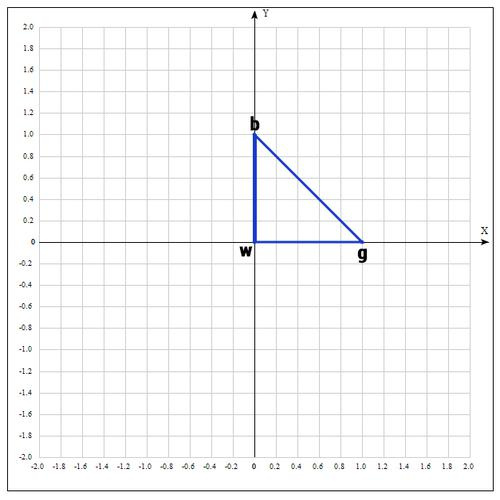
Example:

Find the extremum of the following function: $$

As starting points, take:

$$

We calculate the value of the function at each point:

$$

$$

$$

Rename the points as follows:

$$

Find the middle of the segment bg:

$$

Find the point $$ (reflection operation):

$$

if α = 1, then:

$$

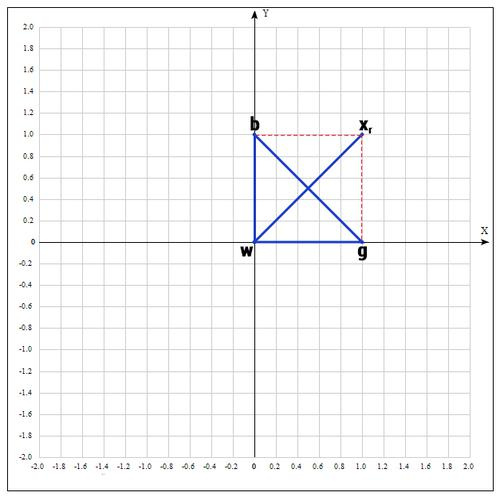
Check point $$:

$$because $$ try to increase the segment (operation stretching).

$$

if γ = 2, then:

$$

$$

Check the value of the function at the point $$:

$$

It turned out that the point $$“Better” than point b. Therefore, we get new vertices:

$$

And the algorithm starts over.

Table of values ​​for 10 iterations:

Best	Good	Worst
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$

Analytically find the extremum of the function, it is reached at the point$$.
After 10 iterations, we get a fairly accurate approximation:$$

More about the method:

The Nelder-Mead algorithm is mainly used to select a parameter in machine learning. In essence, the simplex method is used to optimize model parameters. This is due to the fact that this method optimizes the target function rather quickly and efficiently (especially where shrink modification is not used).

On the other hand, due to the lack of a theory of convergence, in practice the method can lead to an incorrect answer even on smooth (continuously differentiable) functions. It is also possible that the working simplex is far from the optimal point, and the algorithm performs a large number of iterations, while changing the function slightly. A heuristic method for solving this problem is to run the algorithm several times and limit the number of iterations.

Implementation in python programming language:

We create the auxiliary class Vector and overload the operators to be able to perform basic operations with vectors. I intentionally did not use auxiliary libraries to implement the algorithm, as in this case, perception is often reduced.

#!/usr/bin/python
# -*- coding: utf-8 -*-
class Vector(object):
    def __init__(self, x, y):
        """ Create a vector, example: v = Vector(1,2) """
        self.x = x
        self.y = y
    def __repr__(self):
        return "({0}, {1})".format(self.x, self.y)
    def __add__(self, other):
        x = self.x + other.x
        y = self.y + other.y
        return Vector(x, y)
    def __sub__(self, other):
        x = self.x - other.x
        y = self.y - other.y
        return Vector(x, y)
    def __rmul__(self, other):
        x = self.x * other
        y = self.y * other
        return Vector(x, y)
    def __truediv__(self, other):
        x = self.x / other
        y = self.y / other
        return Vector(x, y)
    def c(self):
        return (self.x, self.y)
# objective function
def f(point):
    x, y = point
    return x**2 + x*y + y**2 - 6*x - 9*y
def nelder_mead(alpha=1, beta=0.5, gamma=2, maxiter=10):
    # initialization
    v1 = Vector(0, 0)
    v2 = Vector(1.0, 0)
    v3 = Vector(0, 1)
    for i in range(maxiter):
        adict = {v1:f(v1.c()), v2:f(v2.c()), v3:f(v3.c())}
        points = sorted(adict.items(), key=lambda x: x[1])
        b = points[0][0]
        g = points[1][0]
        w = points[2][0]
        mid = (g + b)/2
        # reflection
        xr = mid + alpha * (mid - w)
        if f(xr.c()) < f(g.c()):
            w = xr
        else:
            if f(xr.c()) < f(w.c()):
                w = xr
            c = (w + mid)/2
            if f(c.c()) < f(w.c()):
                w = c
        if f(xr.c()) < f(b.c()):
            # expansion
            xe = mid + gamma * (xr - mid)
            if f(xe.c()) < f(xr.c()):
                w = xe
            else:
                w = xr
        if f(xr.c()) > f(g.c()):
            # contraction
            xc = mid + beta * (w - mid)
            if f(xc.c()) < f(w.c()):
                w = xc
        # update points
        v1 = w
        v2 = g
        v3 = b
    return b
print("Result of Nelder-Mead algorithm: ")
xk = nelder_mead()
print("Best poits is: %s"%(xk))

Thanks for reading the article. I hope she was useful to you and you learned a lot.
FUNNYDMAN was with you. Good optimization!)