Red-black trees: short and clear

The story of life. The girl invited her boyfriend-programmer to take a psychological test:

Girl: Draw a tree.
Programmer: (draws a binary tree)
Girl: No, another.
Programmer: I can draw a red-black tree.

So, today I want to talk a little about red-black trees. The story will be short, without considering balancing algorithms when inserting / deleting elements in red-black trees.


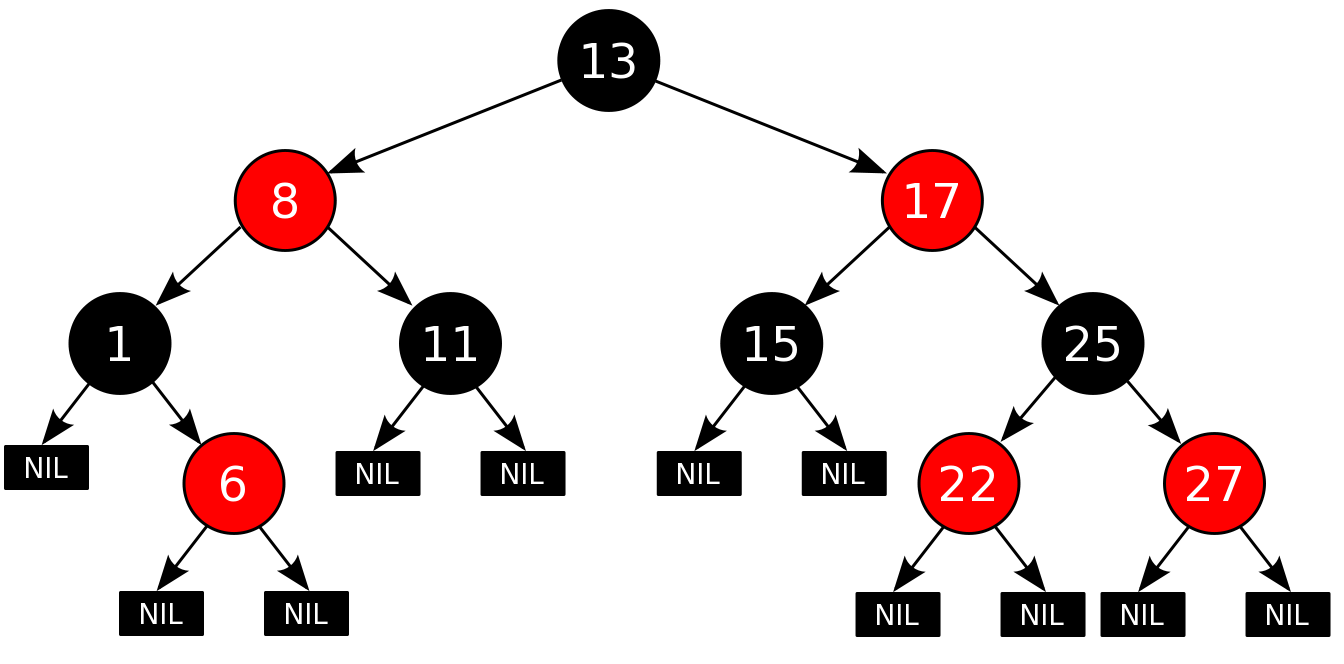
Red and black trees are balanced binary search trees.

Like a binary tree, red-black has the following properties:

1) Both subtrees are binary search trees.

2) For each node with a key$$ the ordering criterion is satisfied:

keys of all left descendants <= $$ <keys of all right descendants

(in other definitions, duplicates should be located on the right side or not at all).
This inequality must be true for all descendants of the node, and not just its child nodes.

Properties of red-black trees:

1) Each node is colored either red or black (an additional field appears in the node data structure - a bit of color).

2) The root is painted black.

3) Leaves (the so-called NULL nodes) are painted black.

4) Each red node must have two black child nodes. It should be noted that a black node may have black child nodes. Red nodes as children can have only black nodes.

5) The paths from the node to its leaves should contain the same number of black nodes (this is the black height).

Well, why is such a tree balanced?

Indeed, red-black trees do not guarantee strict balance (the height difference between two subtrees of any node should not exceed 1), as in AVL trees . But compliance with the properties of red-black wood allows you to perform insert, delete and select operations in time$$. And now let's see if this is true.

Let us have a red-black tree. Black height is equal$$(black height).

If the path from the root node to the leaf node contains the minimum number of red nodes (i.e. zero), then this path is equal to$$.

If the path contains the maximum number of red nodes ($$ according to property $$), then this path will be equal $$.

That is, the paths from the root to the leaves can differ no more than by half ($$, where h is the height of the subtree), this is sufficient for the execution time of operations in such a tree to be $$

How is the insertion done?

Insertion into a red-black tree begins with the insertion of an element, as in a regular binary search tree. Only here are elements inserted at the position of NULL leaves. The inserted node is always colored red. Next is the procedure for checking the preservation of the properties of red-black wood$$.

Property 1 is not violated, since the new node is immediately assigned a red color.

Property 2 is violated only if we had an empty tree and the first inserted node (aka root) is painted red. It is enough to simply repaint the root in black here.

Property 3 is also not violated, because when you add a node, it receives black leafy NULL nodes.

Basically, there are 2 other violations:

1) The red node has a red child node (property violated$$)

2) The paths in the tree contain a different number of black nodes (property violated$$)

Read more about balancing red-black wood in different cases (there are five of them, if you enable violation of the property$$) can be read on the wiki .

Is it generally used somewhere?

Yes! When they read “Algorithms and Data Structures” at the institute in their third year, I could not imagine that red-black trees are used somewhere. I remember how we did not like the theme of balanced trees. Oh, these kindred ties in red-black trees ("uncle", "grandfather", "black brother and godfather red father"), Santa Barbara is direct. Right and left, small and large rotations of AVL trees are continuous roller coasters. You also do not like red-black trees? So you just don’t know how to cook them. And someone just picked it up and cooked it. So, for example, associative arrays in most libraries are implemented through red-black trees.

That is all I wanted to tell.