Some dictionary internals in CPython (and PyPy)
The internal structure of dictionaries in Python is not limited to bucket and closed hashing alone. This is an amazing world of shared keys, caching hashes, DKIX_DUMMY and quick comparisons that can be made even faster (at the cost of a bug with an approximate probability of 2 ^ -64).
If you don’t know the number of elements in the newly created dictionary, how much memory is spent on each element, why now (CPython 3.6 and further) the dictionary is implemented with two arrays and how does this relate to maintaining the insertion order, or simply did not watch the presentation of Raymond Hettinger “Modern Python Dictionaries A confluence of a great dozen great ideas. ” Then welcome.
However, people familiar with the lecture may also find some details and up-to-date information, and for completely newbies who are not familiar with buckets and closed hashing, the article will also be interesting.
CPython dictionaries are everywhere, they are based on classes, global variables, kwargs parameters, the interpreter creates thousands of dictionaries , even if you yourself have not added a single brace to your script. But for solving many applied tasks, dictionaries are also used, it is not surprising that their implementation continues to improve and become increasingly overgrown with various tricks.
If you are familiar with how standard Hashmap and private hashing work, you can skip to the next chapter.
The idea behind the dictionaries is simple: if we have an array in which objects of the same size are stored, then we can easily access the necessary object, knowing the index.
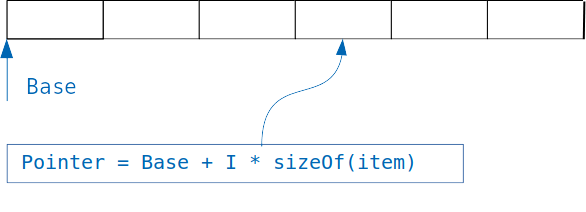
We simply add the index multiplied by the size of the object to the offset of the array, and get the address of the desired object.
But what if we want to organize a search not by an integer index, but by a variable of another type, for example, to find users at their email address?
In the case of a simple array, we will have to look through the mail of all users in the array and compare them with the desired one, this approach is called linear search and, obviously, it is much slower than accessing an object by index.
Linear searches can be significantly accelerated if we limit the size of the area in which to search. This is usually achieved by taking the remainder of the hash . The field by which the search is carried out - key.
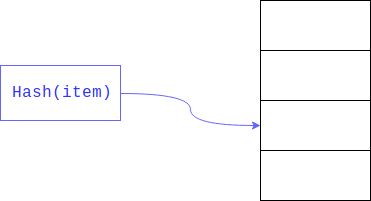
As a result, linear search is carried out not over the entire large array, but according to its part.
But what if there is already an element there? This could very well happen, since no one guaranteed that the residuals from dividing a hash would be unique (like the hash itself). In this case, the object will be placed at the next index, if it is also occupied, it will be shifted by one more index and so until it finds a free one. When retrieving an item, all keys with the same hash will be viewed.
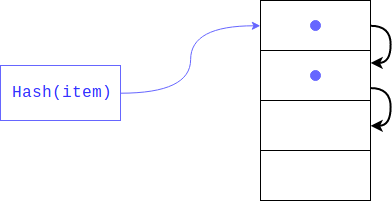
This type of hash is called closed. If there are few free cells in the dictionary, then such a search threatens to degenerate into a linear one, respectively, we lose all the gain, for which the dictionary was created, to avoid this, the interpreter keeps the array filled 1/2 - 2/3. If there are not enough free cells, then a new array is created twice as large as the previous one and the elements from the old one are transferred to the new one by one.
What to do if the item has been deleted? In this case, an empty cell is formed in the array and the search algorithm by the key cannot distinguish, this cell is empty because there was no element with such a hash in the dictionary, or because it was deleted. To avoid data loss during deletion, the cell is marked with a special flag (DKIX_DUMMY). If this flag is encountered during the search for an item, the search will continue, the cell is considered to be occupied, and if inserted, the cell will be overwritten.
Each dictionary element must contain a link to the target object and a key. The key must be stored for handling collisions, the object - for obvious reasons. Since both the key and the object can be of any type and size, we cannot store them directly in the structure, they are in dynamic memory, and references to them are stored in the structure of the list element. That is, the size of one element must be equal to the minimum size of two pointers (16 bytes on 64-bit systems). However, the interpreter also stores the hash, this is done in order not to recompute it with each increase in the size of the dictionary. Instead of calculating the hash of each key in a new way and taking the remainder of dividing by the number of buckets, the interpreter simply reads the already stored value. But, What if the key object was changed? In this case, the hash should be recalculated and the stored value will be incorrect? Such a situation is impossible, since mutable types cannot be keys of a dictionary.
The structure of the dictionary element is defined as follows:
The minimum size of the dictionary is declared constant PyDict_MINSIZE, which is equal to 8. The developers decided that this is the optimal size in order to avoid unnecessary memory consumption for storing null values and time for dynamic expansion of the array. Thus, when creating a dictionary (prior to version 3.6), you needed at least 8 elements in the dictionary * 24 bytes in the structure = 192 bytes (this is without taking into account the other fields: expenses for the dictionary type variable itself, the number of elements count, etc.)
Dictionaries are also used to implement custom class fields. Python allows you to dynamically change the number of attributes, this dynamic does not require additional costs, since adding / deleting an attribute is essentially equivalent to the corresponding dictionary operation. However, this functionality is used by a minority of programs, the majority is limited to the fields declared in __init__. But each object must keep its dictionary, with its keys and hashes, despite the fact that they coincide with other objects. The logical improvement here is the storage of shared keys in only one place, which is what was implemented in the PEP 412 - Key-Sharing Dictionary. The ability to dynamically change the dictionary did not disappear: if the order changes or the number of keys is changed, the dictionary is converted from the dividing key to the usual one.
To avoid collisions, the maximum "load" of the dictionary is 2/3 of the current size of the array.
Thus, the first expansion will occur after the addition of the 6th element.
The array turns out to be quite discharged, while the program is running from half to one third of the cells remain empty, which leads to increased memory consumption. In order to circumvent this restriction and, if possible, to store only the necessary data, a newlevel of abstraction array was added .
Instead of storing a flat array, for example:
Starting from version 3.6, the dictionaries are organized as follows:
Those. only those records that are really needed are stored, they are moved from the hash table to a separate array, and only the indexes of the corresponding records are stored in the hash table. If initially the array took 192 bytes, then now only 80 (3 * 24-bytes for each record + 8 bytes per indices). 58% compression achieved. [2]
The element size in indices also changes dynamically, initially it is equal to one byte, that is, the entire array can be placed in one register, when the index starts to fit into 8 bits, then the elements expand to 16, then to 32 bits. There are special constants DKIX_EMPTY and DKIX_DUMMY, for the empty and deleted elements, respectively, the expansion of the indexes to 16 bytes occurs when the elements in the dictionary becomes more than 127.
New objects are added to the entries, that is, when expanding the dictionary, there is no need to move them, you just need to increase the size of indices and refill it with indices.
When iterating over the dictionary, the array of indices is not needed, the elements are sequentially returned from the entries, since elements are added to the end of the entries each time, the dictionary automatically preserves the order of entries. Thus, in addition to reducing the required memory for storing the dictionary, we obtained faster dynamic expansion and preservation of the order of keys. Reducing memory is good in and of itself, but at the same time it can increase speed, as it allows a greater number of entries to get into the processor’s cache.
CPython developers liked this implementation so much that dictionaries are now required to maintain the insertion order by specification. If earlier the order of dictionaries was determined, i.e. was strictly defined by the hash and was unchanged from launch to launch, then a bit of randomness was added to it so that the keys went differently each time, now the dictionary keys are required to maintain order. How much it was necessary, and what to do if there will be an even more efficient implementation of the dictionary, but not preserving the order of insertion, is unclear.
However, and so there were requests to implement a mechanism for preserving the order of attribute declaration in classes and in kwargs , this implementation makes it possible to close these problems without special mechanisms.
Here it looks inCPython code :
But the iteration is more complicated than one could initially think of, there are additional mechanisms for checking that the dictionary was not changed during the iteration, one of them is the version of the dictionary as a 64-bit number that each dictionary stores.
Finally, consider the mechanism for resolving collisions. The fact is that in python, hash values are easily predictable:
And since during the creation of the dictionary from these hashes, the remainder of the division is taken, then in essence it determines in which bucket the record is written, only the last few bits of the key (if it is integer). You can imagine a situation where we have a lot of objects “want” to get into neighboring buckets, in this case, when searching, we will have to look through a lot of objects that are not in their proper places. To reduce the number of collisions and increase the number of bits that determine which batch the recording goes to, the following mechanism has been implemented:
perturb is an integer variable initialized by the hash. It should be noted that in the case of a large number of collisions it is reset to zero and the following index is calculated by the formula:
When an item is retrieved from the dictionary, the same search is performed: the slot index is calculated in which the item should be located; if the slot is empty, then the exception “value not found” is thrown. If there is a value in this slot, it is necessary to check that its key corresponds to the desired one, this may well not be executed if a collision occurs. However, almost any object can be the key, including one for which the comparison operation takes considerable time. In order to avoid a lengthy comparison operation, several tricks have been applied in Python:
Pointers are compared first, if the key pointer of the object being searched for is equal to the pointer of the object being searched, that is, pointing to the same memory area, then the comparison immediately returns true. But that's not all. As it is known, equal objects should have equal hashes, which means that objects with different hashes are not equal. After checking the pointers, hashes are checked, if they are not equal, false will be returned. And only if the hashes are equal, an honest comparison will be called.
What is the probability of such an outcome? Approximately 2 ^ -64, of course, because of the easy predictability of the hash value, you can easily find an example, but in reality, this check doesn’t happen often, how much? Raymond Hettinger put together an interpreter by modifying the last comparison operation with a simple return true. Those. the interpreter considered objects equal if their hashes are equal. After that, he set automated tests on such an interpreter for many popular projects that were completed successfully. It may seem strange to consider objects with equal hashes equal, not to additionally check their contents, and to rely solely on the hash, but you do it regularly when using git or torrent protocols. They consider files (file blocks) equal, if their hashes are equal, which may well lead to errors, but their creators (and all of us) hope
Now you should have a definitive structure of the dictionary, which looks like this:
In the previous chapter, we considered what has already been implemented and can be used by everyone in their work, but the improvements are not limited to these: plans for version 3.8 are support for reversed dictionaries . Indeed, instead of iterating from the beginning of the array of elements and increasing the indices, nothing prevents starting from the end and decreasing the indices.
For a deeper immersion in the subject, it is recommended to read the following materials:
If you don’t know the number of elements in the newly created dictionary, how much memory is spent on each element, why now (CPython 3.6 and further) the dictionary is implemented with two arrays and how does this relate to maintaining the insertion order, or simply did not watch the presentation of Raymond Hettinger “Modern Python Dictionaries A confluence of a great dozen great ideas. ” Then welcome.
However, people familiar with the lecture may also find some details and up-to-date information, and for completely newbies who are not familiar with buckets and closed hashing, the article will also be interesting.
CPython dictionaries are everywhere, they are based on classes, global variables, kwargs parameters, the interpreter creates thousands of dictionaries , even if you yourself have not added a single brace to your script. But for solving many applied tasks, dictionaries are also used, it is not surprising that their implementation continues to improve and become increasingly overgrown with various tricks.
Basic implementation of dictionaries (via Hashmap)
If you are familiar with how standard Hashmap and private hashing work, you can skip to the next chapter.
The idea behind the dictionaries is simple: if we have an array in which objects of the same size are stored, then we can easily access the necessary object, knowing the index.

We simply add the index multiplied by the size of the object to the offset of the array, and get the address of the desired object.
But what if we want to organize a search not by an integer index, but by a variable of another type, for example, to find users at their email address?
In the case of a simple array, we will have to look through the mail of all users in the array and compare them with the desired one, this approach is called linear search and, obviously, it is much slower than accessing an object by index.
Linear searches can be significantly accelerated if we limit the size of the area in which to search. This is usually achieved by taking the remainder of the hash . The field by which the search is carried out - key.

As a result, linear search is carried out not over the entire large array, but according to its part.
But what if there is already an element there? This could very well happen, since no one guaranteed that the residuals from dividing a hash would be unique (like the hash itself). In this case, the object will be placed at the next index, if it is also occupied, it will be shifted by one more index and so until it finds a free one. When retrieving an item, all keys with the same hash will be viewed.

This type of hash is called closed. If there are few free cells in the dictionary, then such a search threatens to degenerate into a linear one, respectively, we lose all the gain, for which the dictionary was created, to avoid this, the interpreter keeps the array filled 1/2 - 2/3. If there are not enough free cells, then a new array is created twice as large as the previous one and the elements from the old one are transferred to the new one by one.
What to do if the item has been deleted? In this case, an empty cell is formed in the array and the search algorithm by the key cannot distinguish, this cell is empty because there was no element with such a hash in the dictionary, or because it was deleted. To avoid data loss during deletion, the cell is marked with a special flag (DKIX_DUMMY). If this flag is encountered during the search for an item, the search will continue, the cell is considered to be occupied, and if inserted, the cell will be overwritten.
Implementation Features in Python
Each dictionary element must contain a link to the target object and a key. The key must be stored for handling collisions, the object - for obvious reasons. Since both the key and the object can be of any type and size, we cannot store them directly in the structure, they are in dynamic memory, and references to them are stored in the structure of the list element. That is, the size of one element must be equal to the minimum size of two pointers (16 bytes on 64-bit systems). However, the interpreter also stores the hash, this is done in order not to recompute it with each increase in the size of the dictionary. Instead of calculating the hash of each key in a new way and taking the remainder of dividing by the number of buckets, the interpreter simply reads the already stored value. But, What if the key object was changed? In this case, the hash should be recalculated and the stored value will be incorrect? Such a situation is impossible, since mutable types cannot be keys of a dictionary.
The structure of the dictionary element is defined as follows:
typedefstruct {
Py_hash_t me_hash; // хеш
PyObject *me_key; // указатель на ключ
PyObject *me_value; // указатель на хранимый объект
} PyDictKeyEntry;
The minimum size of the dictionary is declared constant PyDict_MINSIZE, which is equal to 8. The developers decided that this is the optimal size in order to avoid unnecessary memory consumption for storing null values and time for dynamic expansion of the array. Thus, when creating a dictionary (prior to version 3.6), you needed at least 8 elements in the dictionary * 24 bytes in the structure = 192 bytes (this is without taking into account the other fields: expenses for the dictionary type variable itself, the number of elements count, etc.)
Dictionaries are also used to implement custom class fields. Python allows you to dynamically change the number of attributes, this dynamic does not require additional costs, since adding / deleting an attribute is essentially equivalent to the corresponding dictionary operation. However, this functionality is used by a minority of programs, the majority is limited to the fields declared in __init__. But each object must keep its dictionary, with its keys and hashes, despite the fact that they coincide with other objects. The logical improvement here is the storage of shared keys in only one place, which is what was implemented in the PEP 412 - Key-Sharing Dictionary. The ability to dynamically change the dictionary did not disappear: if the order changes or the number of keys is changed, the dictionary is converted from the dividing key to the usual one.
To avoid collisions, the maximum "load" of the dictionary is 2/3 of the current size of the array.
#define USABLE_FRACTION(n) (((n) << 1)/3)Thus, the first expansion will occur after the addition of the 6th element.
The array turns out to be quite discharged, while the program is running from half to one third of the cells remain empty, which leads to increased memory consumption. In order to circumvent this restriction and, if possible, to store only the necessary data, a new
Instead of storing a flat array, for example:
d = {'timmy': 'red', 'barry': 'green', 'guido': 'blue'} # ->
entries = [['--', '--', '--'],
[-8522787127447073495, 'barry', 'green'],
['--', '--', '--'],
['--', '--', '--'],
['--', '--', '--'],
[-9092791511155847987, 'timmy', 'red'],
['--', '--', '--'],
[-6480567542315338377, 'guido', 'blue']]
Starting from version 3.6, the dictionaries are organized as follows:
indices = [None, 1, None, None, None, 0, None, 2]
entries = [[-9092791511155847987, 'timmy', 'red'],
[-8522787127447073495, 'barry', 'green'],
[-6480567542315338377, 'guido', 'blue']]
Those. only those records that are really needed are stored, they are moved from the hash table to a separate array, and only the indexes of the corresponding records are stored in the hash table. If initially the array took 192 bytes, then now only 80 (3 * 24-bytes for each record + 8 bytes per indices). 58% compression achieved. [2]
The element size in indices also changes dynamically, initially it is equal to one byte, that is, the entire array can be placed in one register, when the index starts to fit into 8 bits, then the elements expand to 16, then to 32 bits. There are special constants DKIX_EMPTY and DKIX_DUMMY, for the empty and deleted elements, respectively, the expansion of the indexes to 16 bytes occurs when the elements in the dictionary becomes more than 127.
New objects are added to the entries, that is, when expanding the dictionary, there is no need to move them, you just need to increase the size of indices and refill it with indices.
When iterating over the dictionary, the array of indices is not needed, the elements are sequentially returned from the entries, since elements are added to the end of the entries each time, the dictionary automatically preserves the order of entries. Thus, in addition to reducing the required memory for storing the dictionary, we obtained faster dynamic expansion and preservation of the order of keys. Reducing memory is good in and of itself, but at the same time it can increase speed, as it allows a greater number of entries to get into the processor’s cache.
CPython developers liked this implementation so much that dictionaries are now required to maintain the insertion order by specification. If earlier the order of dictionaries was determined, i.e. was strictly defined by the hash and was unchanged from launch to launch, then a bit of randomness was added to it so that the keys went differently each time, now the dictionary keys are required to maintain order. How much it was necessary, and what to do if there will be an even more efficient implementation of the dictionary, but not preserving the order of insertion, is unclear.
However, and so there were requests to implement a mechanism for preserving the order of attribute declaration in classes and in kwargs , this implementation makes it possible to close these problems without special mechanisms.
Here it looks inCPython code :
struct _dictkeysobject {
Py_ssize_t dk_refcnt;
/* Size of the hash table (dk_indices). It must be a power of 2. */
Py_ssize_t dk_size;
/* Function to lookup in the hash table (dk_indices):
- lookdict(): general-purpose, and may return DKIX_ERROR if (and
only if) a comparison raises an exception.
- lookdict_unicode(): specialized to Unicode string keys, comparison of
which can never raise an exception; that function can never return
DKIX_ERROR.
- lookdict_unicode_nodummy(): similar to lookdict_unicode() but further
specialized for Unicode string keys that cannot be the <dummy> value.
- lookdict_split(): Version of lookdict() for split tables. */
dict_lookup_func dk_lookup;
/* Number of usable entries in dk_entries. */
Py_ssize_t dk_usable;
/* Number of used entries in dk_entries. */
Py_ssize_t dk_nentries;
/* Actual hash table of dk_size entries. It holds indices in dk_entries,
or DKIX_EMPTY(-1) or DKIX_DUMMY(-2).
Indices must be: 0 <= indice < USABLE_FRACTION(dk_size).
The size in bytes of an indice depends on dk_size:
- 1 byte if dk_size <= 0xff (char*)
- 2 bytes if dk_size <= 0xffff (int16_t*)
- 4 bytes if dk_size <= 0xffffffff (int32_t*)
- 8 bytes otherwise (int64_t*)
Dynamically sized, SIZEOF_VOID_P is minimum. */char dk_indices[]; /* char is required to avoid strict aliasing. *//* "PyDictKeyEntry dk_entries[dk_usable];" array follows:
see the DK_ENTRIES() macro */
};
But the iteration is more complicated than one could initially think of, there are additional mechanisms for checking that the dictionary was not changed during the iteration, one of them is the version of the dictionary as a 64-bit number that each dictionary stores.
Finally, consider the mechanism for resolving collisions. The fact is that in python, hash values are easily predictable:
>>>[hash(i) for i in range(4)]
[0, 1, 2, 3]
And since during the creation of the dictionary from these hashes, the remainder of the division is taken, then in essence it determines in which bucket the record is written, only the last few bits of the key (if it is integer). You can imagine a situation where we have a lot of objects “want” to get into neighboring buckets, in this case, when searching, we will have to look through a lot of objects that are not in their proper places. To reduce the number of collisions and increase the number of bits that determine which batch the recording goes to, the following mechanism has been implemented:
// вместо простого
i = i + 1 % n
// был реализован следующий:
#define PERTURB_SHIFT 5
perturb >>= PERTURB_SHIFT;
j = (5*j) + 1 + perturb;
// использовать значение j % n в качестве следующего индексаperturb is an integer variable initialized by the hash. It should be noted that in the case of a large number of collisions it is reset to zero and the following index is calculated by the formula:
j = (5 * j + 1) % n
When an item is retrieved from the dictionary, the same search is performed: the slot index is calculated in which the item should be located; if the slot is empty, then the exception “value not found” is thrown. If there is a value in this slot, it is necessary to check that its key corresponds to the desired one, this may well not be executed if a collision occurs. However, almost any object can be the key, including one for which the comparison operation takes considerable time. In order to avoid a lengthy comparison operation, several tricks have been applied in Python:
# псевдокод алгоритма (на самом деле там, разумеется C)defeq(key, entity):if id(key) == id(entity): returnTrueif hash(key) != hash(entity): returnFalsereturn key == entity
Pointers are compared first, if the key pointer of the object being searched for is equal to the pointer of the object being searched, that is, pointing to the same memory area, then the comparison immediately returns true. But that's not all. As it is known, equal objects should have equal hashes, which means that objects with different hashes are not equal. After checking the pointers, hashes are checked, if they are not equal, false will be returned. And only if the hashes are equal, an honest comparison will be called.
What is the probability of such an outcome? Approximately 2 ^ -64, of course, because of the easy predictability of the hash value, you can easily find an example, but in reality, this check doesn’t happen often, how much? Raymond Hettinger put together an interpreter by modifying the last comparison operation with a simple return true. Those. the interpreter considered objects equal if their hashes are equal. After that, he set automated tests on such an interpreter for many popular projects that were completed successfully. It may seem strange to consider objects with equal hashes equal, not to additionally check their contents, and to rely solely on the hash, but you do it regularly when using git or torrent protocols. They consider files (file blocks) equal, if their hashes are equal, which may well lead to errors, but their creators (and all of us) hope
Now you should have a definitive structure of the dictionary, which looks like this:
typedefstruct {
PyObject_HEAD
/* Number of items in the dictionary */
Py_ssize_t ma_used;
/* Dictionary version: globally unique, value change each time
the dictionary is modified */uint64_t ma_version_tag;
PyDictKeysObject *ma_keys;
/* If ma_values is NULL, the table is "combined": keys and values
are stored in ma_keys.
If ma_values is not NULL, the table is splitted:
keys are stored in ma_keys and values are stored in ma_values */
PyObject **ma_values;
} PyDictObject;
Future changes
In the previous chapter, we considered what has already been implemented and can be used by everyone in their work, but the improvements are not limited to these: plans for version 3.8 are support for reversed dictionaries . Indeed, instead of iterating from the beginning of the array of elements and increasing the indices, nothing prevents starting from the end and decreasing the indices.
Additional materials
For a deeper immersion in the subject, it is recommended to read the following materials:
- Record of the report at the beginning of the article
- Proposal for a new implementation of dictionaries
- CPython dictionary source code
