Multi-armed bandit in the task of finding objects in a video stream

On Habré the subject of application of so-called "bandits" for data mining has already been repeatedly touched upon. In contrast to the already familiar training of machines on precedents, which is often used in recognition problems, a multi-armed bandit is used to build, in a sense, “recommendation” systems. On Habré the idea of ​​a multi-armed bandit and its applicability to the task of recommending Internet content has already been very detailed and accessible. In our next post, we wanted to tell you about the symbiosis of learning by precedent and learning with reinforcement in the problems of recognizing a video stream.

Consider the problem of detecting a geometrically rigid object in a video stream. In the distant 2001 first year, Paul Viola and Michael Jones proposed a detection algorithm (hereinafter we will call it the Viola and Jones method [1]), with which you can search for such objects in separate images in a split second. Although the algorithm was originally developed to solve the problem of searching for faces, today it is successfully used in various areas of machine vision where real-time detection is needed.

But what to do when it is required to search for several objects of different types in the video stream? In such cases, usually several different Viola and Jones detectors are trained and applied independently on the frames of the video stream, thereby slowing down the search procedure proportionally to the number of objects the number of times. Fortunately, in practice, quite often a situation arises when, despite a large number of acceptable objects, at each moment in time there is no more than one desired object on the frame. As an example, let’s take a real task from our practice, acquired during the painstaking creation of Smart IDReader . Using a web camera, a bank employee registers bank cards issued to customers, and it is required to determine the type of card and recognize the number by the logo applied. Despite the fact that at present there are more than ten different types of payment systems (and therefore more than 10 different logos), at each time the operator shows only one card.

The multi-armed bandit problem

The initial form of the n-hand bandit problem is formulated as follows. Let it be necessary to repeatedly choose one of n different alternatives (options). Each choice entails a certain reward, depending on the chosen action. The average reward for choosing an action is called the value of the action. The purpose of the sequence of actions is to maximize the expected total reward for a given period of time. Often each such attempt is called a game.

Although the exact values ​​of the value of the actions are not known, their estimates can be obtained with each new game. Then at every moment of time there is at least one action for which such an estimate will be the greatest (such actions are called greedy). Application refers to the choice of a greedy action in the next game. Learning is understood as the choice of one of the non-greedy actions in this game with the aim of more accurately assessing the value of the non-greedy action.

Denote by V _t (a) the estimated value of the value of action a in the t-th game. If, at time t of the beginning of the t-th game, action a was chosen k _a time, which led to the sequential receipt of a reward r ₁ , r ₂, ..., r _ka , then the value of the action for all k _a > 0 will be estimated by the formula:


Despite the fact that it is easiest in each game to choose an action that has the maximum expected value, this approach does not lead to success due to the lack of a research procedure. There are many ways to get rid of this problem. Some of them are very simple and quickly come to mind every mathematician. Some of them have already been outlined here on Habré. In any case, we believe that it would be more correct not to compress a mathematically beautiful theory into the scale and formats of Habr, but to provide a respected reader with a link to the available literature [2].

The task of choosing a recognition detector

So, back to our task of finding objects in a video stream. Let there be a video fragment containing T frames. Each frame of a video sequence can contain no more than one object that needs to be detected. A total of N different types of objects, and each type has its own cascade of Viola and Jones. Objects in a video sequence appear and disappear in a natural way, there is no instant appearance or disappearance of objects (for example, in the task of registering bank cards using a web camera described in the introduction, naturalness consists in a smooth sequential appearance and disappearance of a card in a frame). It is necessary to construct an algorithm for choosing a detector (we denote it by the letter a) for each frame of the video fragment, which provides the most accurate detection of objects.

In order to be able to compare different detector selection algorithms, it is necessary to determine the quality functional Q (a) . The better our algorithm “selects” the recognition detector for the next frame, the higher the value of the functional should be. Then, omitting the mathematics (you can always find it in our full version of the article [3]), we will calculate the functional as the number of correctly recognized frames of the video sequence.

Detector greedy algorithm

We proceed directly to the description of the algorithm, which, recall, operates with a machine learning tool with reinforcement.

If in the multi-armed bandit problem the reward arises naturally, then in the object search problem the concept of “reward” requires a separate definition. It is intuitively clear that the reward for choosing an action (recognition cascade) must be positive if it was possible to find the object correctly, and zero otherwise. However, at the time of the game there is no reliable information about the objects available on the frames, since otherwise the task of finding objects in the image does not make sense. Then, assuming that the target object detectors have good accuracy and completeness, we will encourage the selection of the appropriate detector only for the objects found in the image (that is, the reward in the next game is 1 when the object is on the frame and 0 otherwise).

Now consider a way to calculate the value of an action. The formula presented in the description of a multi-armed bandit is only suitable for stationary tasks (when the system does not change with time). In non-stationary tasks, later rewards have higher priority than earlier ones. The most common way to do this is to use an exponential average. Then the value of the action a when receiving the next reward r _{k + 1} is determined by the following recursive formula:


where α is the step size (the larger the value of α, the greater the weight in the value of the action has a new reward). From a physical point of view, the parameter α controls how quickly the current action becomes greedy.

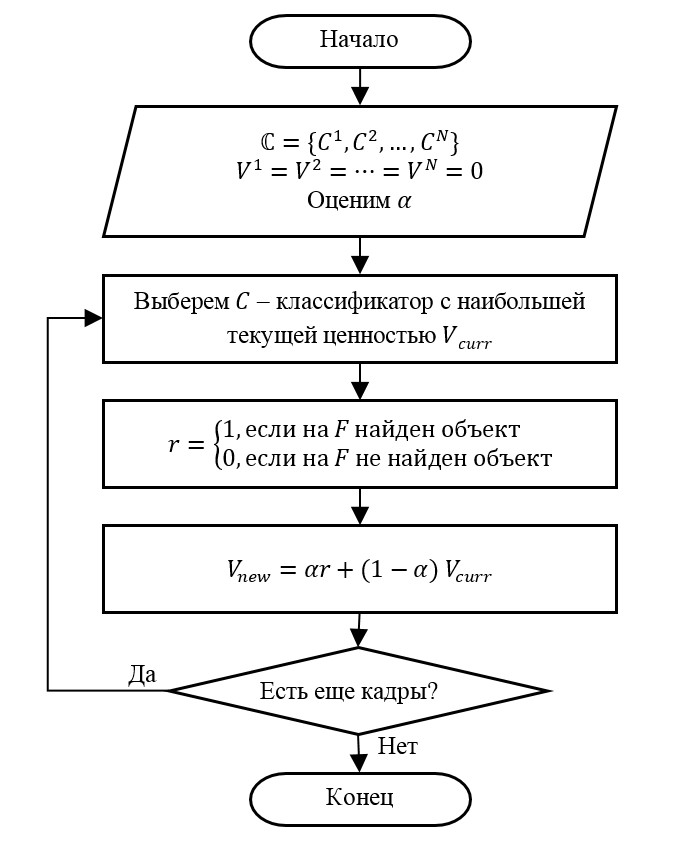
Based on the foregoing, the adaptive detector selection algorithm can be represented as the following sequence of steps.

Step 1 (Initialization). Suppose there are N detectors. We set the initial value of the value for the detector V ₁ = V ₂ = ⋯ = V _N = 0. We choose the value of the parameter α.

Step 2. Select detector C with the maximum current value of the value V _curr . If there are several such detectors, we will choose one of them at random.

Step 3. Apply at the next frame F selected detector C . We determine the gain of detector r in accordance with the introduced rule (that is, r = 1 if there is an object on F ).

Step 4. Update the value of the value V _new for the detector C according to the recursive formula presented above.

Step 5. Go to step 2, if there are still frames for searching for objects. Otherwise, we finish processing.

Experimental results

As we said at the very beginning, we used this algorithm to solve the problem of determining the type of bank card in a video stream. The operator presents a bank card to the web-camera, and the recognition system should determine the type of card by the existing logo.


To assess the quality of the proposed algorithm, we prepared a test video fragment containing 29 representations of bank cards of the following five types: VISA, MasterCard, American Express, Discover and UnionPay. The total number of frames of the video fragment was 1116. The frame composition of the test video fragment is presented in the table. We ourselves pre-trained the logo detectors of payment systems using the Viola and Jones method (of course, on completely different images).

Object type	Number of cards	Total number of frames
VISA	16	302
Mastercard	8	139
American express	2	37
Unionpay	1	17
Discovery	2	34
Frames without a card	-	587
TOTAL	29th	1116

The effectiveness of the proposed detector selection algorithm (AED) was evaluated in comparison with a sequential algorithm (trained logo detectors are applied to frames in turn). Such a sequential algorithm is quite meaningful and implements the idea of ​​accelerating detection by thinning. The table shows the value of the quality functional Q , as well as the ratio of the quality functional to the total number of processed frames Q _r for individual interval points.

Method	300	600	900	1116
Alternate	191 (0.64)	379 (0.63)	547 (0.61)	676 (0.61)
AVD	216 (0.72)	446 (0.74)	682 (0.76)	852 (0.76)

A graphical representation of the tabular data presented is shown in the following figure.

Despite the fact that the described detector selection algorithm provides better detection quality compared to the alternate method, the ideal quality is still not achieved. This is partly due to their own quality parameters of the used cascades of Viola and Jones (determined by accuracy and completeness). To confirm this, we conducted an experiment on the simultaneous use of all logo detectors for each frame (of course, not paying attention to time in this case). As a result of this experiment, the maximum possible value of the quality functional Q ^* = 1030 ( Q _r ^* = 0.92) was obtained , which essentially indicates the need for training new, more accurate detectors :-)

Conclusion

In the tasks of searching for objects in a video stream, the processing speed of a single frame is important. There are problems for which even the application of fast algorithms, such as the Viola and Jones method, does not provide the necessary speed. In such cases, sometimes the combination of various machine learning methods (such as use case training and reinforcement learning) allows you to elegantly solve the problem without resorting to over-optimization of algorithms and unscheduled upgrade of iron.

List of references

1. Viola P., Jones M. Robust Real-time Object Detection // International Journal of Computer Vision. 2002.
   
2. Sutton R.S., Barto E.G. Reinforced training. M .: BINOM. Laboratory of Knowledge, 2012.399 p.
   
3. Usilin S.A. Using the pursuit method to improve the performance of the multiclass detection algorithm for objects in a video stream by Viola-Jones cascades // Transactions of the Institute for System Analysis of the Russian Academy of Sciences (ISA RAS). 2017. No. 1 (67). C. 75–82.