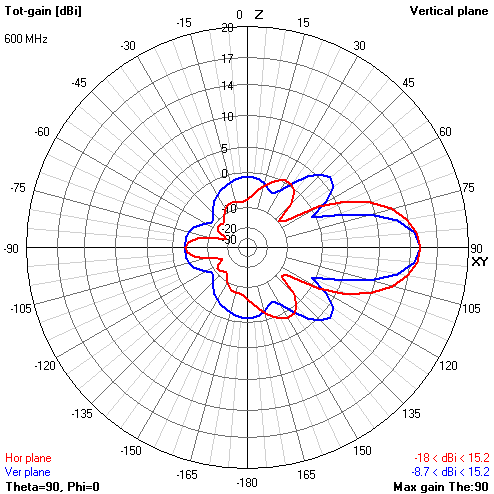
BowTie Cone Antenna Theory
Foreword
The issue of cone antennas (butterfly, BowTie) is very poorly covered in the literature, although this is the most popular type of TV antenna in the world, along with Uda-Yagi.
Therefore, in the article we describe the principles of their work and design: the wave properties of a single butterfly vibrator, the influence of reflectors and directors on the radiation pattern and antenna gain, the principles of connecting butterfly vibrators to common-mode arrays.
In addition, we present to the reader 7 practical designs of television antennas based on a butterfly vibrator that are well optimized with CAD from the simplest (including reflector-free) to a very high-performance antenna with an average gain of 16.3 dBi for long-distance reception.
At the base of all antennas there is always an active element (vibrator, radiator), to which voltage is applied during transmission operation, or voltage is removed during reception operation.
In most types of antennas, the vibrator is a half-wave dipole and its varieties (split dipole, loop, double loop, quarter-wave pin, a set of dipoles with log-periodic geometry, etc.).
The design of spurious elements and the matching of the antenna proceed from the properties of the vibrator. The properties of a half-wave dipole are well known and widely described. The radiation resistance is 73Ω at the center frequency, the radiation pattern is almost circular, with a small gain of 2.15 dBi perpendicular to the axis.
The axis of the dipole passes through the E-plane, i.e. the polarization of the radiation coincides with the axis of the dipole.
The radiation resistance decreases rapidly with decreasing frequency and increases with increasing frequency.
A dipole centered at 600 MHz with SWR = 1 per 73Ω line will have SWR = 2 already at frequencies of 560 and 650 MHz, i.e. maintains an acceptable SWR in the range of -7% ... + 8%.
The dipole is ideal for narrow-band applications, and you can make it broadband only in compromise ways - add spurious elements (reflectors, directors), choosing their geometry so as to equalize the wave resistance in different parts of the range. With this selection of geometry, the gain of a multi-element antenna will be significantly lower than with the same number of spurious elements optimized for a narrow range. The antenna gain is very uneven over the range, and the SWR goes beyond the limits of decency at the edges of the range.
Part I. Cone Vibrator (BowTie radiator)
There are other designs of vibrators, the so-called PNA - frequency-independent. Their radiation resistance is much less dependent on the frequency; they can operate in a relatively wide frequency range with high efficiency and acceptable SWR.
One of these designs is a biconical antenna:
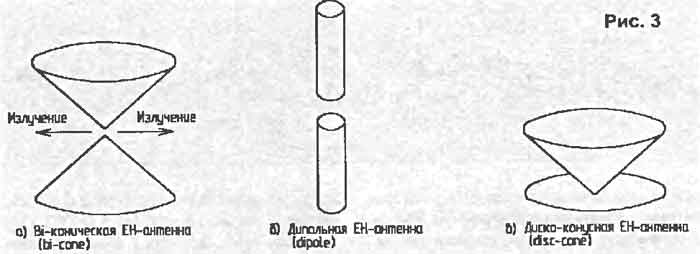
Its properties are preserved if, instead of volumetric cones, their projections are applied - flat triangles in the form of a bow tie (BowTie).
If the triangles are infinite - the antenna will work at all frequencies:
If you create triangles of finite size - they will be able to work in some large frequency range.

Moreover, the triangle does not have to be solid.

Its properties are preserved even when only two beams are left from the plane, although in the presence of jumpers, the triangle emits a little better.
3D view, BowTie solid, BowTie whiskers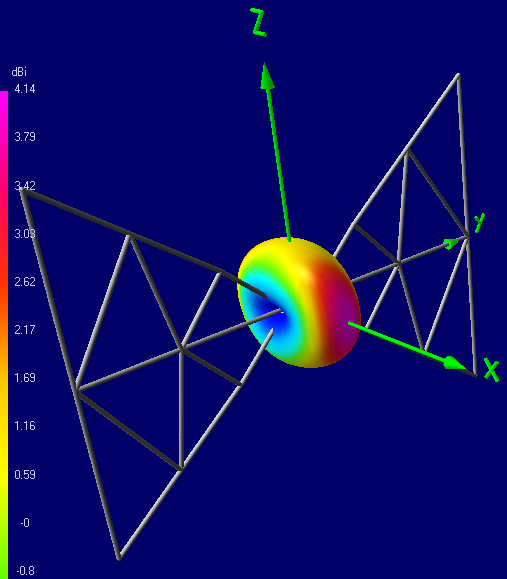



Next, we will consider only the option of two whiskers (Eng. - Whiskers) - the simplest and most common.
The central frequency for BowTie is such a wavelength when each of the 4 whiskers has a length of ~ 0.47λ (with a technological gap in the center of 1 "= 2.5 cm).
This means that the BowTie vibrator is approximately 2 times larger than a half-wave dipole. The total width of the dipole - ~ 0.5λ, and the full width of BowTie is ~ 1λ.
Such dimensions make it unacceptably large at frequencies below 200 MHz, therefore it is not used on TV channels 1-5 and is not used in FM radio reception.
For frequencies 200 ... 800 MHz it the dimensions are quite acceptable, which in combination with broadband ensured mass, and in the segment of ten 10+ dBi dominance.
Complex wave impedance, Z Ω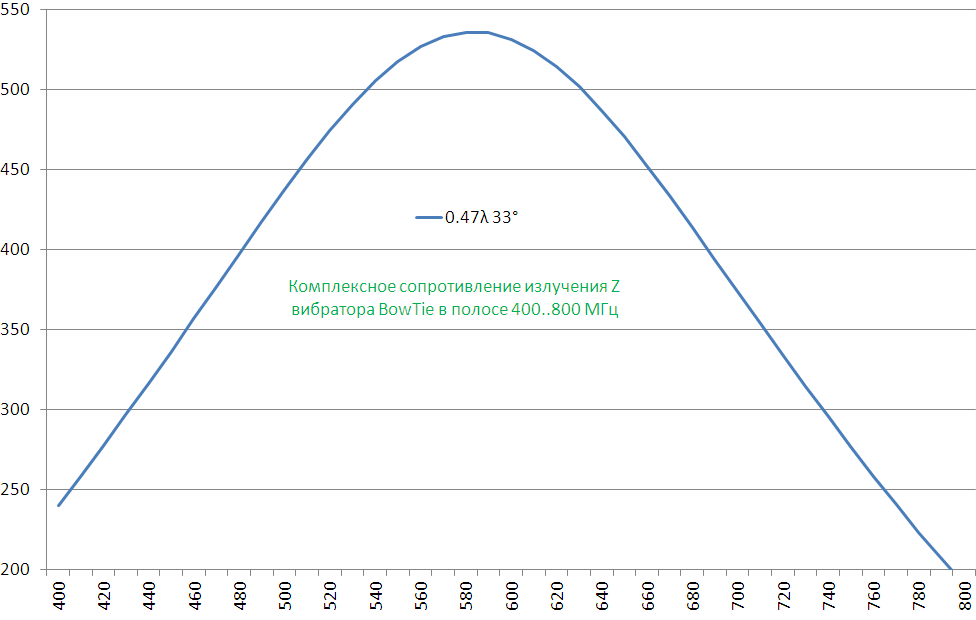

The complex radiation resistance at the central frequency (all examples will be for 600 MHz) is about 545Ω (for the diameter of the conductors 2.8 mm) and gradually drops to 200Ω at frequencies of 350 and 800 MHz.
Matching 545Ω to a 75Ω coaxial line is very non-standard (although it can be implemented if necessary), but for working in a wide band of frequencies it is both unnecessary and even undesirable. An acceptable SWR for television would be if you use power from 300 to 600Ω. The minimum SWR averaged in the range 470 ... 790 MHz is obtained if ~ 400Ω is supplied.
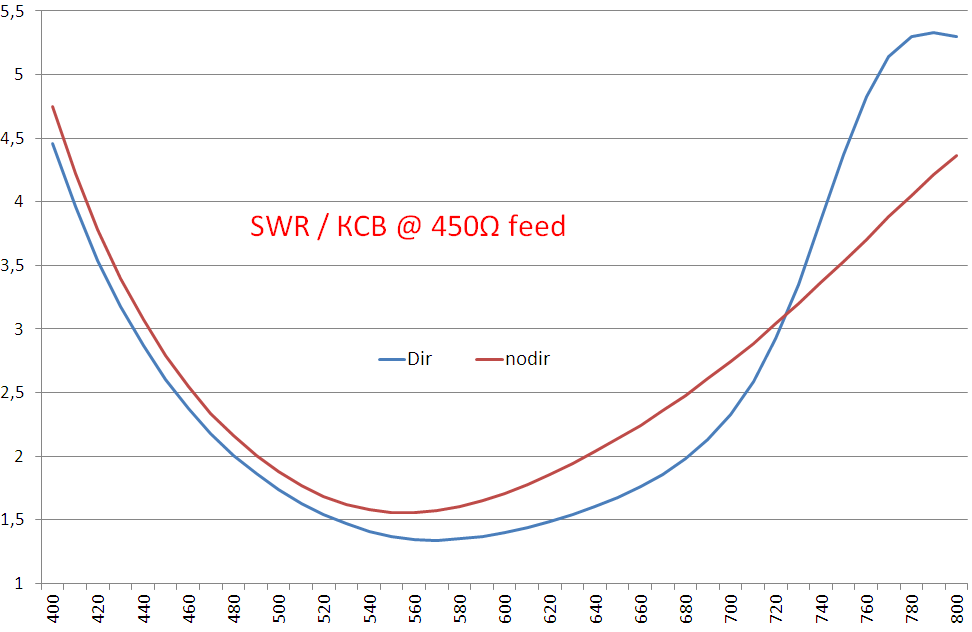
Here is the SWR (eng. - SWR) in the frequency band 400. 800 MHz with 400Ω power supply, and a comparison with the SWR of the half-wave dipole on the 73Ω line.
SWR / SWR BowTie

The graph shows options with a mustache opening angle of 20 to 60 degrees. The angle is not much affected, the optimal angle is about 33 degrees. If the classical dipole allows you to keep SWR <2 in the band 560 ... 650 MHz, then the BowTie vibrator has an SWR <2 in the band 470 ... 690 MHz, i.e. covers the entire UHF TV range (in the future, channels 49 and above will be sold for LTE-700 after the SECAM broadcast is stopped), and in the frequency band up to 790 MHz it has an SWR <3, which is also acceptable.
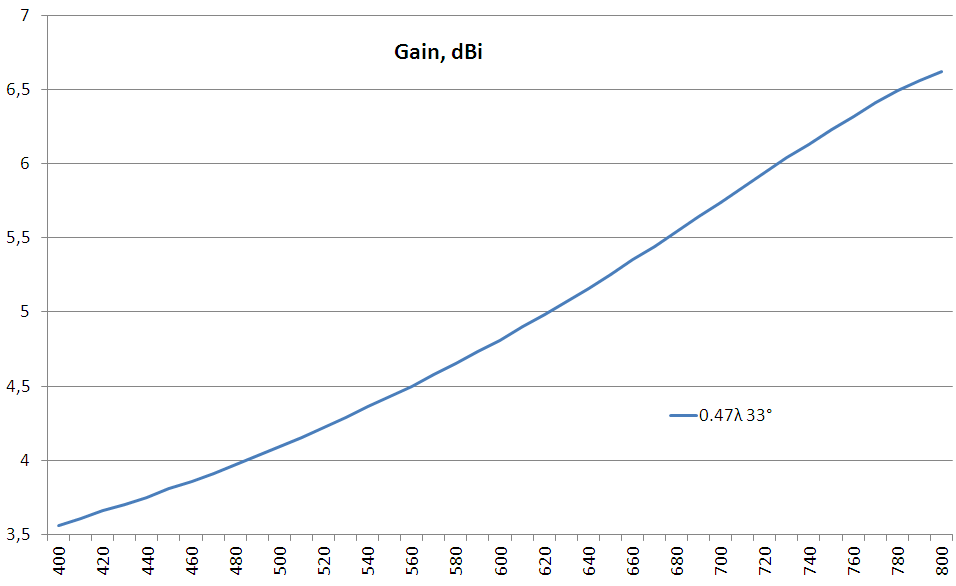
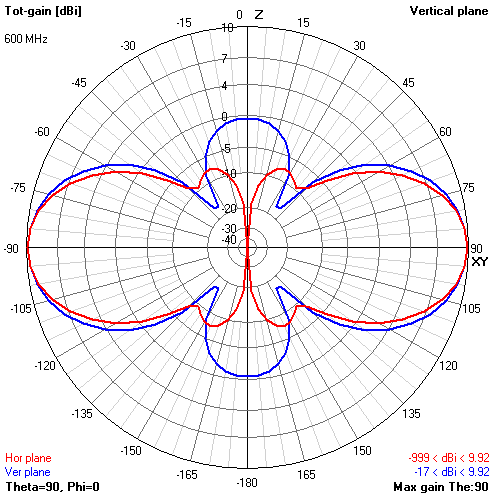
The radiation pattern of BowTie is slightly different from the dipole. Up / Down BowTie emits 3-4 dB fainter than forward / backward. On the side, it suppresses radiation much more than a classical dipole. Due to this, the forward / backward gain at the central frequency is about 4.8 dBi (versus the 2.15 dBi dipole), and in the frequency band 400 ... 800 MHz it gradually increases from 3.6 dBi to 6.7 dBi.
Gain pattern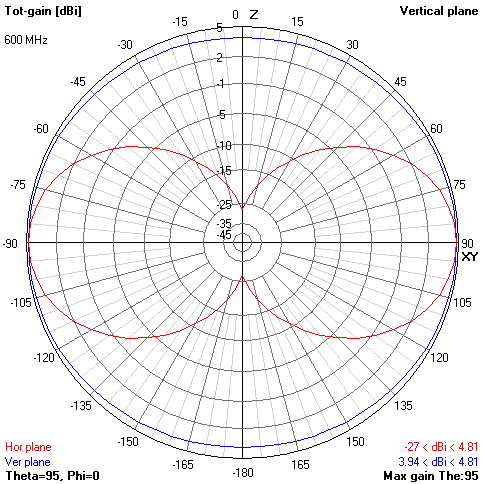


To match a 75Ω cable with a single BowTie, the optimal 6: 1 balun (Bal-Un, Balanced-Unbalanced transformer), which can be made from a 4: 1 balun or by performing on a 2-hole ring:
Balun 6: 1
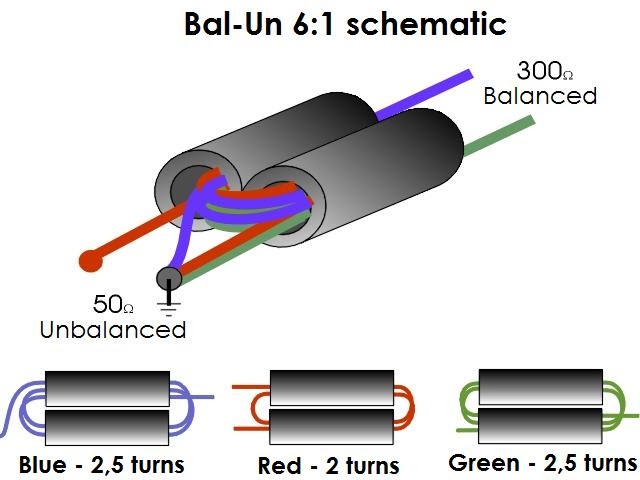


A standard 300Ω 4: 1 balun will also work, but an SWR will be> 2.
Part Ia Cone Vibrator - All-Wave?
The cone antenna is partly of the PNA (frequency independent antenna) and UWB (Ultra-Wide Band) type of antenna.
The cone vibrator has the maximum radiation resistance with a length of 0.47λ whiskers (about 545Ω), with a deviation of the length in either direction - the resistance drops to a minimum of 84Ω (at 0.31λ).
Further shortening of the wave again leads to an increase in resistance to 545Ω at a whisker length multiple of 0.47λ (600, 1200, 1800, 2400 MHz), and to a cyclic drop to 84Ω at a whisker length multiple of 0.47λ, but with a fixed shift of 0.24λ (900, 1500, 2100, 2700 MHz).
0.47λ@600 Mhz, Impedance in 300 .. 4000 Mhz band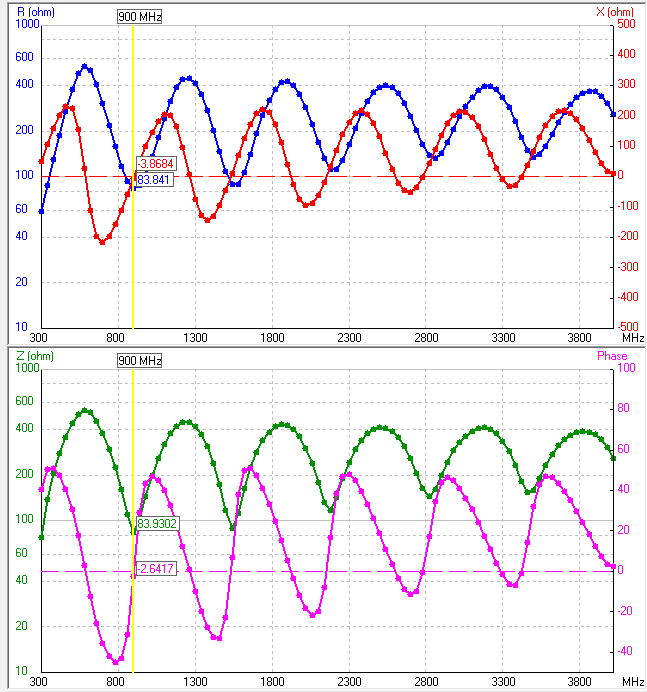

Thus, if we have the ability to match the impedance in the range of 84-545Ω, the antenna can be used in a very wide frequency range, unlike a dipole in which the resistance will increase infinitely or fall at low frequencies to zero.
The practical benefit of this property of cone antennas can only be obtained with an active matching device installed directly next to the antenna, which will convert 84-545Ω to 50 or 75Ω resistance of the transmission lines of the radio and / or transmitter.
With passive matching through a fixed transformer, it is practically impossible to benefit from such broadband properties. An acceptable SWR is maintained in a relatively narrow frequency range, although it is wider than that of a conventional dipole. If according to SWR = 2, the matching range is + -8% for a dipole, then for a conical vibrator + -18%.
What is the resonant frequency for the butterfly vibrator? To answer this question, we return to the definitions first.
Here is a model of any abstract antenna: The

total (complex) radiation resistance is equal to the sum of the real part (blue) and imaginary part (red).
The imaginary part consists of two reactive components: inductive (with a + sign) and capacitive (with a - sign).
When the inductive and capacitive reactances are equal, the imaginary part is zero. The antenna impedance is equal to the actual radiation resistance. This frequency is called the resonant frequency of the antenna. For a half-wave dipole, the resonance length of the dipole is 0.5λ (taking into account the end capacitance in thick conductors - about 0.47λ, the exact value depends on the L / D ratio), the real resistance at the resonant frequency is 73Ω.
For a butterfly vibrator, there are two resonances when the inductive component is zero: these are the points of both the maximum resistance and the minimum. Those. for a vibrator at 600 MHz, the frequencies 600, 1200, 1800 and 900, 1500, 2100, etc. will be resonant. With a resonance length of each whisker that is a multiple of 0.47λ (with an aperture angle of 33 degrees and a conductor diameter of 2.8 mm), the vibrator resistance is the maximum possible (in the region of 600Ω), and with a multiple length of 0.47λ * K + 0.24λ (quarter-wave shift) is minimal possible (around 85Ω).
The exact value of the real resistance R is very sensitive to the diameter of the conductors from which the mustache is made. With a very thin conductor D = 0.1 mm, the resistance R at the resonant frequency reaches 1444Ω, and with a mustache with a diameter of 10 mm it reaches only 345Ω. The resonant frequency is also shifted.
Here is a table of the dependences Rmax (at the resonant frequency), Rmin (at frequencies with a shift of 1/4 from the first resonance) and the length of the whiskers corresponding to these frequencies, depending on the diameter of the conductor.

For a conventional dipole, the diameter of the conductor has almost no effect on the resonance resistance, and a thick dipole reduces the reactive component - it makes the impedance curve more gentle, and the dipole itself is wider.
For a butterfly vibrator, the diameter of the conductor has a very strong effect on both the resonant and reactive, and therefore impedance.
Compare the curves of the total (complex) resistance Z for a vibrator with a mustache of 4x223 mm, diameter 1, 3 and 6 mm.
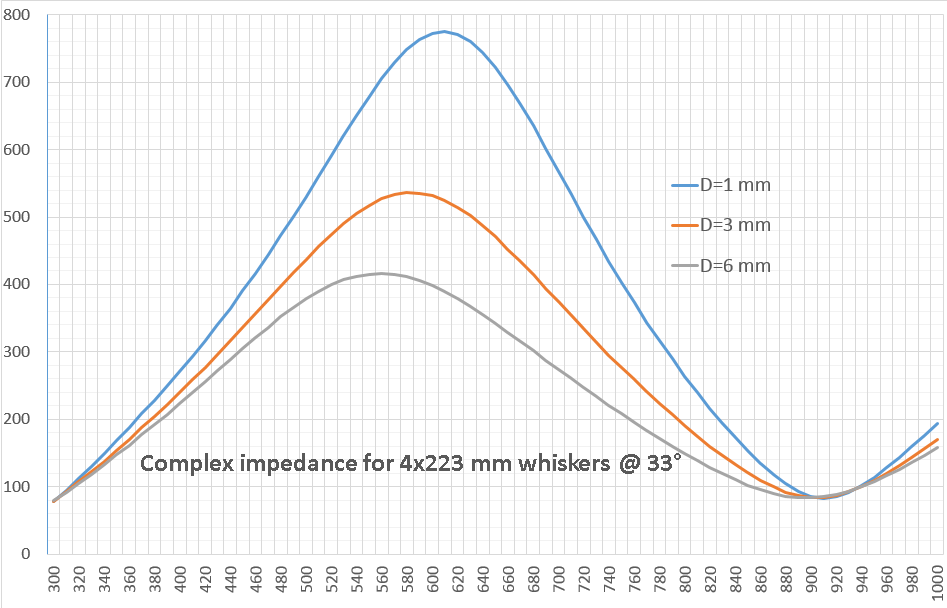
As you can see, the diameter significantly affects Rmax, and almost does not affect Rmin. In addition, increasing the diameter of the mustache reduces the resonant frequency (i.e., the mustache can be made shorter).
A thicker vibrator has less slope steepness and less resistance drop in the frequency range. This makes it easy to calculate matching for a wide range of frequencies.
Part Ib Cone Vibrator - Beam in the frequency band
As we know, an ordinary dipole has the same DD throughout the frequency band and does not depend on the distance from the resonant frequency. Is this for a butterfly vibrator?
DN in the 1st and near the 2nd resonant frequencies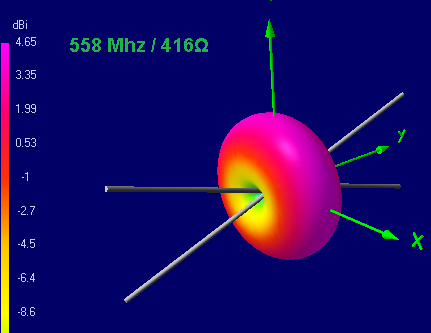


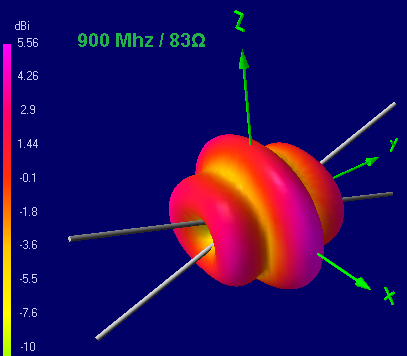
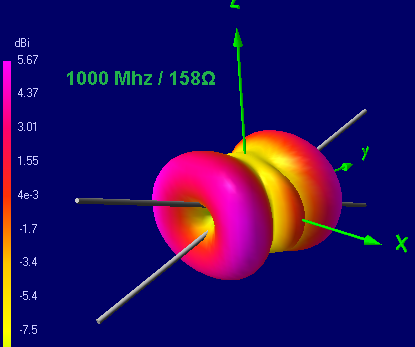
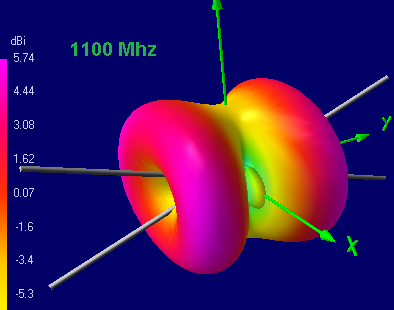
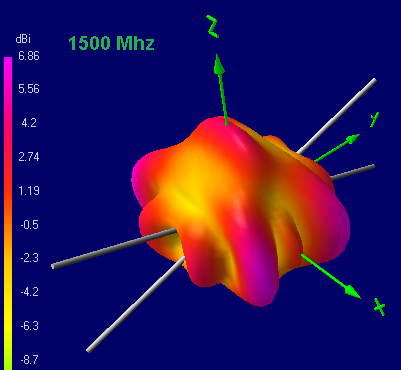







As you can see, with increasing frequency, the diagram narrows first, and starting from about 0.62λ, the side lobes begin to grow, the intensity of which at a frequency near the second resonance reaches the intensity of the main lobe, and with a further increase in frequency, the main lobe almost disappears. With the passage of each subsequent resonant frequency, the petals bifurcate and the radiation petals appear upward.
Conclusion: although formally the butterfly vibrator is all-wave, the shape of the radiation pattern begins to bifurcate after more than 1 wavelength is laid in the total length of the vibrator (both whiskers). Although the vibrator will emit, but the direction of this radiation is unsuitable for practical applications.
The practical range from above is limited by a radiation pattern with a length of 0.6λ.
From below it is limited by a drop in radiation resistance and an increase in SWR. With a mustache length shorter than 0.19λ, R drops below 25Ω, and the SWR rises to 4+ even when powered by 50 / 75Ω.
Suitable for practical use (when solving the issue of impedance matching) is the wavelength range from 0.2-0.6λ, i.e. +28% ..- 57% of the resonant frequency 0.47λ
Part II / Parasites
Spurious elements are conductors that lie in the E-plane, i.e. parallel to the vibrator and lie in the polarization of the radiation of the vibrator and are electrically isolated from the vibrator.
Metal connection is allowed only for points with zero potential and is only structural in nature.
Parasites significantly affect the dipole, and the effect depends on whether the parasite is longer or shorter than the vibrator. If the parasite is shorter, then it has capacitive reactivity and increases radiation towards itself, and if the parasite is longer, it has inductive reactivity and “repels” the radiation from itself. Short parasites are called directors, and long parasites are called reflectors. The more parasites and the closer they are to the dipole, the lower its radiation resistance.
Already 1 reflector greatly reduces radiation back and forth and down and adds forward. Radiation forward increases from 2.15 dBi +4.7 dB = 6.9 dBi.
If the reflector has a vibrator length, then it reduces radiation only up / down, and forward / backward radiation is equivalent.
When the length of the reflector decreases below the length of the vibrator, it turns into a director, the radiation backward exceeds the radiation forward. The gain of 1V1D can reach up to 6.2 dBi (slightly less than 1V1R).
The directors differ from the reflector in that the further addition of the number of directors leads to a further narrowing of the NAM and, accordingly, an increase in gain. The second reflector behind the first has almost no effect on the radiation of the antenna.
With a cone antenna, parasites behave differently. The parasite begins to exhibit any properties with a length of about 0.2λ. Its optimum distance is 0.15λ from the vibrator.
From 0.3 to 0.47λ, the parasite works as a director, with a gain peak at 0.448λ = 8.91 dBi. At 0.47λ, the parasite is neutral (suppresses only the top / bottom), and from 0.48λ and higher (to infinity) it behaves like a reflector, with a gain peak of 0.49λ = 8.52 dBi (+3.71 dB against the bare cone)
0.0λ - 4.81 dBi (without parasite)
0.1λ - 4.83 dBi
0.2λ - 4.94 dBi
0.3λ - 5.32 dBi (works as a director)
0.4λ - 6.89 dBi (works as a director)
0.449λ - 8.92 dBi (works as a director)
0.47λ - 7.57 dBi ( directivity front / back the same)
0.49λ - 8.52 dBi (works as a reflector)
0.5λ - 8.45 dBi (works as a reflector)
0.6λ - 7.18 dBi (and further works as a reflector)
0.7λ - 6.77 dBi
0.8λ - 6.63 dBi
0.9λ - 6.57 dBi
1.0λ - 6.55 dBi
1.2λ - 6.55 dBi
1.3λ - 6.60 dBi
1.4λ - 7.04 dBi
1.5λ - 7.7 dBi
1.6λ - 7.14 dBi
2.0λ - 6.87 dBi
0.49λ Reflector, pattern 3D / ARRL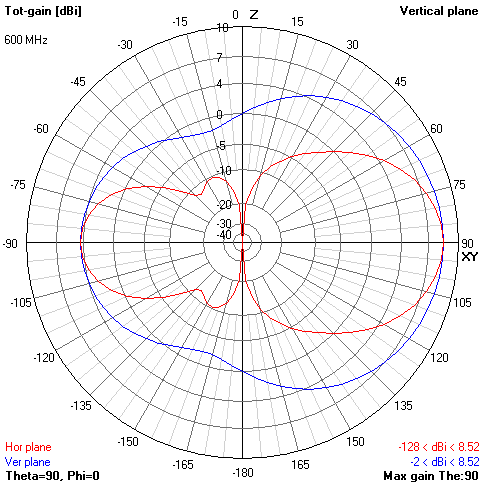



The radiation resistance grows strongly (slightly decreased at the dipole). So the 0.49λ reflector raises the resistance from 545 to 1150Ω. In addition, in a wide band, the properties of the parasite change sharply with the passage of the point 0.47λ. The parasite turns from a reflector into a director and in the right direction the signal is weakened (but the radiation of the rear hemisphere is growing). Therefore, such a design does not make sense for any practical purposes.
In order for the reflector to behave like a reflector in a wide frequency band, it is necessary to take at least 1.0λ at the center frequency. But the characteristics of such an antenna are very mediocre - the front-back KZD is very weak (at some frequencies zero), the SWR exceeds 2.6 at the edges of the range.
Conclusion: parasites in order to create the directivity of the antenna (gain and gain) are very impractical and therefore are not used in practice. Parasites can be carefully used to correct the frequency response in the upper part of the range and to create a blockage of frequencies along the upper edge. So, for example, if for a broadband antenna (like Polish ASP-8) for the band 50 ... 800 MHz we add a director who will have a length of <0.45λ at a frequency of 800 MHz, then at higher frequencies where his effective length is> 0.3λ he will begin to influence:
- it
will increase the radiation resistance (and as we already know, it decreases when you deviate from the center frequency) - it will increase the gain due to the forward direction
- when the length begins to approach 0.47λ, the resistance will increase sharply (and the SWR) and the director will turn into a reflector and reduce the gain forward. The director will work as a notch filter, with a cutoff frequency of F = 300 / L / 0.47 = 141 / L of its length.
At lower frequencies, the length of such a director will be <0.3λ and there will be almost no effect on the operation of the antenna.
Part III / Reflector Screens
The screen reflector is a flat reflector. It can be made both from a solid conductor (sheet of metal, foil) and from a grid of horizontal conductors (if the position of the vibrator mustache is horizontal). Vertical conductors do not affect the properties of the screen. They can only be used for structural reasons to give structural strength.
Like a single parasite, the properties of the screen depend on its width. If the screen has a width of less than 0.47λ, it works as a director: the radiation grows in the direction of such a screen. If the screen has a width of more than 0.47λ, it works like a reflector.
The distance to the reflector can be any from 0.1λ to 0.5λ. With a reflector with a width of 1λ and a height of 0.5λ (± 0.25λ from the radiation axis) with a grid spacing of 0.025λ, the radiation resistance and gain of a single BowTie will be:
0.10λ - 1700Ω - 9.83 dBi
0.15λ - 871Ω - 9.63 dBi
0.20λ - 603Ω - 9.35 dBi
0.25λ - 496Ω - 8.94 dBi
0.30λ - 442Ω - 8.35 dBi
0.35λ - 414Ω - 7.48 dBi
0.40λ - 404Ω - 6.15 dBi
0.45 λ - 412Ω - 4.04 dBi
0.50λ - 443Ω - 0.67 dBi The
reflector offset from 0.15λ to 0.35λ is practically useful. As the screen approaches <0.15λ, the resistance grows very quickly to impractical values. With the removal of> 0.35λ, the directivity decreases rapidly and at 0.42λ the same as that of the bare vibrator.
For operation at the center frequency, the optimal distance is 0.2λ - the resistance is very convenient 600Ω, and the directivity reaches 9.35 dBi. For operation in a wide frequency band, it is possible to select the optimal position in the range 0.15 ... 0.25λ, improving the matching / gain in those parts of the range where a dip is observed.
Consider the influence of the reflector width at Offset = 0.2λ:
0.50λ - 890Ω - 08.95 dBi - 05.86 F / B
0.75λ - 657Ω - 09.11 dBi - 10.57 F / B
1.00λ - 603Ω - 09.35 dBi - 12.37 F / B
1.25λ - 574Ω - 09.90 dBi - 14.46 F / B
1.50λ - 583Ω - 10.18 dBi - 19.33 F / B
1.75λ - 586Ω - 10.04 dBi - 19.77 F / B
2.00λ - 585Ω - 09.96 dBi - 19.48 F / B
With a width of less than 0.47λ the screen behaves like a director and concentrates the radiation in its direction.
With a length of> 0.47λ, the screen behaves like a reflector-reflector; at 0.59λ, the Front / Back ratio reaches 8 dB.
At 1λ, the antenna already has decent parameters - a convenient resistance of 600Ω, gain> 9 dBi and short-circuit resistance> 12 dBi.
With a further increase in the screen width, the gain almost does not increase, but the KZD rises to 18..20 dB.
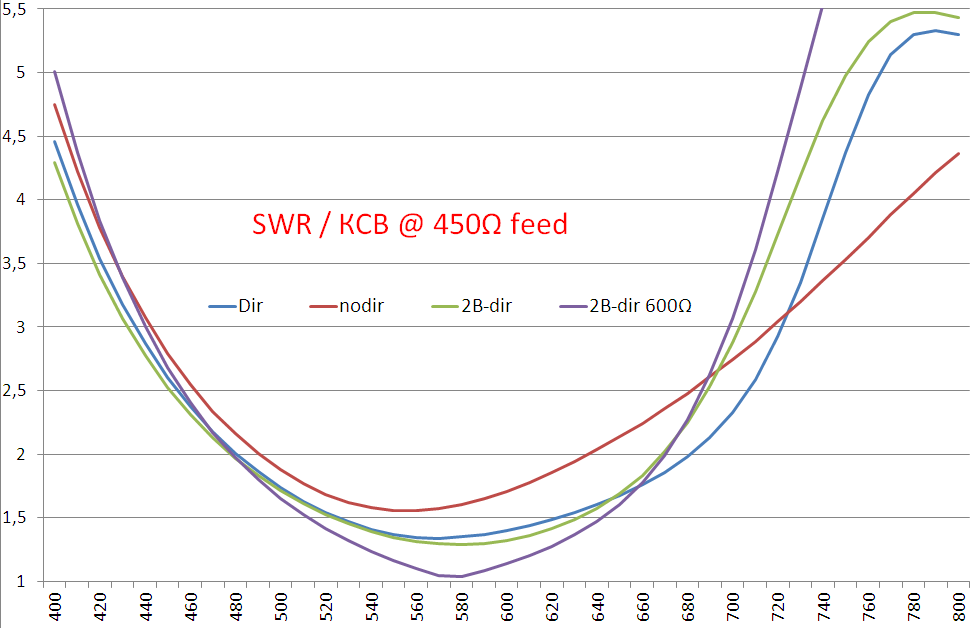
Peak gain and KZD at 1.5λ, further increase no longer gives any increase. In the frequency band 470 ... 690 MHz, the SWR increases too much at the edges of the range with an offset of 0.20λ. If you need to work on any of the channels 21..49, then you need to increase the offset to 0.25λ, then the antenna will have such parameters for a load of 600Ω:
1-bay BowTie + screen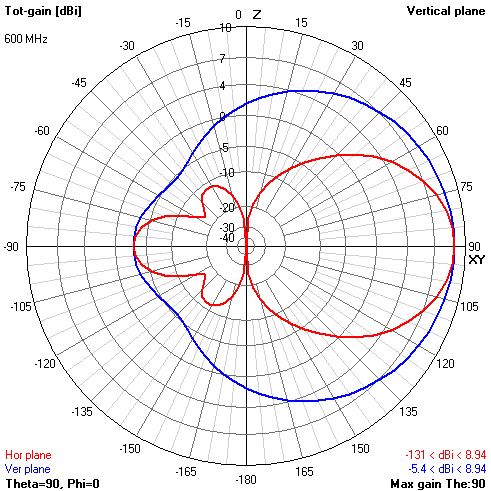
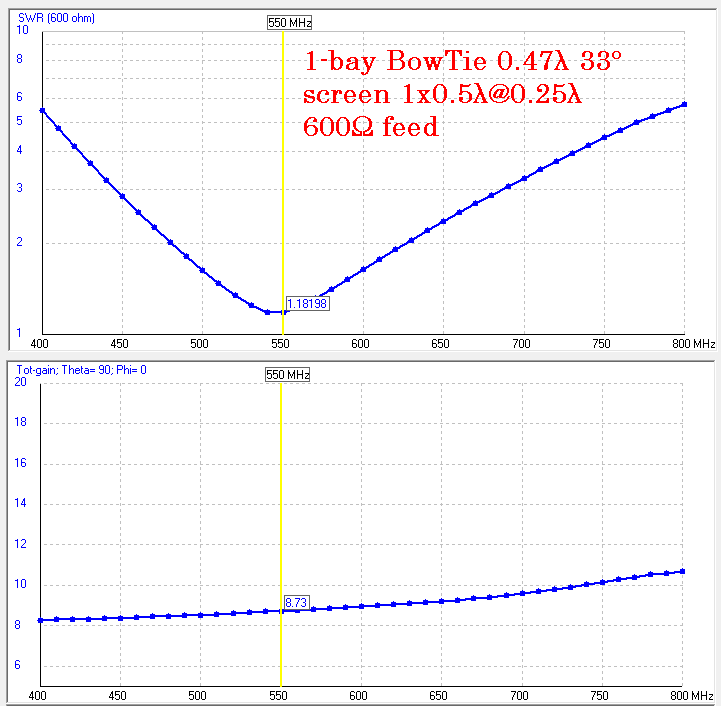
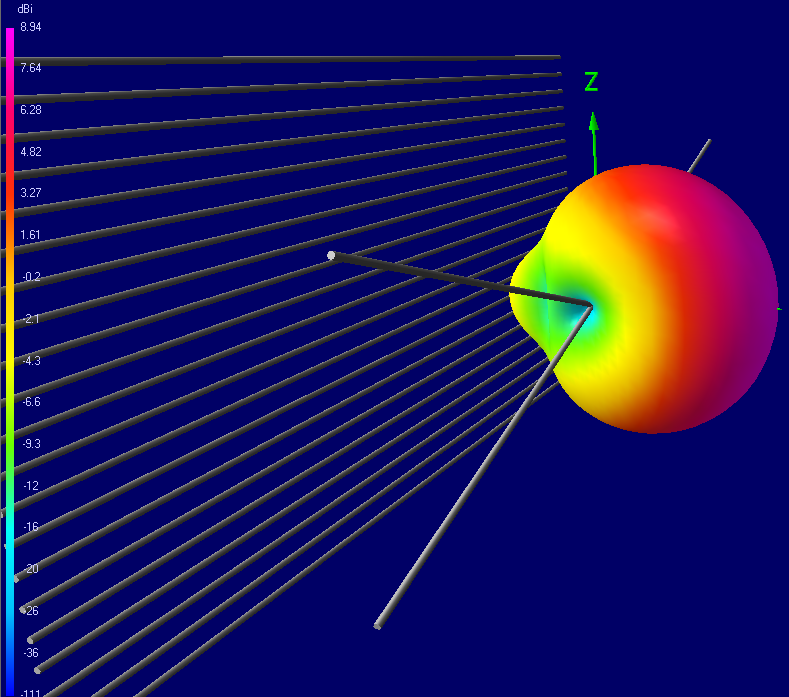



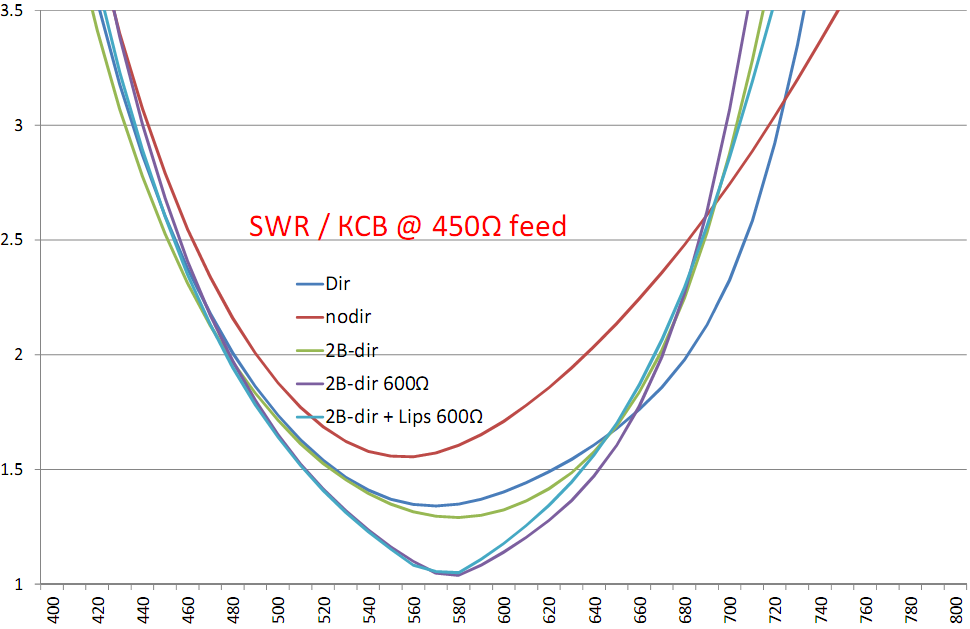
The antenna can work with 4: 1, 6: 1 and 8: 1 baluns. In this case, the SWR will be different in a wide frequency band:
Feed 300Ω vs 450Ω vs 600Ω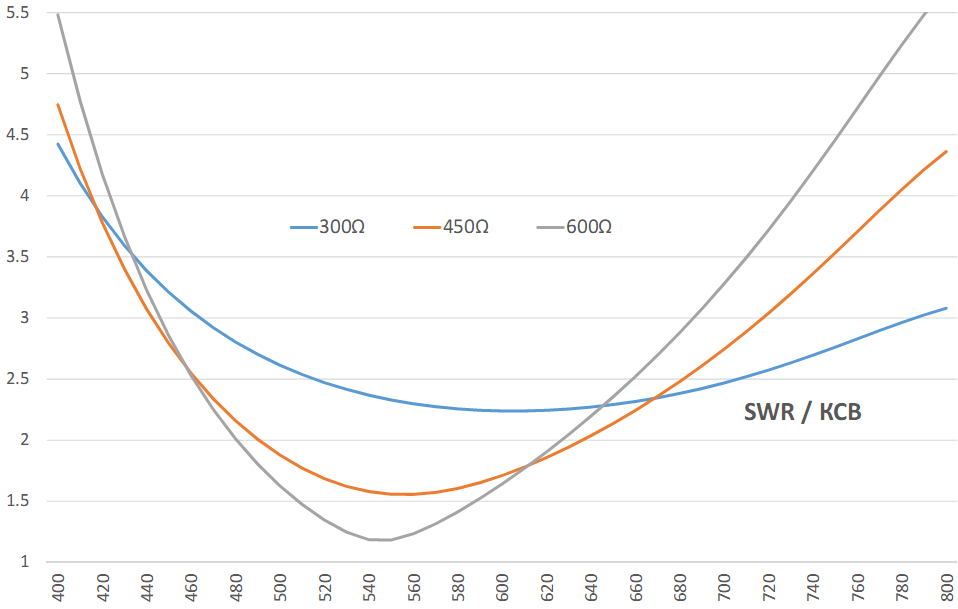

Consider whether a parasite director can be added to such an antenna. As the analysis in the previous part showed, the length of the director should not approach 0.47λ in the entire antenna band.
Suppose we need to design an antenna for the range 470 ... 700 MHz. Take a director with a length of 0.41λ at a frequency of 700 MHz, at the center frequency of the previous antenna (600 MHz) its length will be 0.35λ. The step-by-step optimizer showed that the optimal distance to the vibrator is 0.20λ.
Screen + Director, Gain, SWR, 3D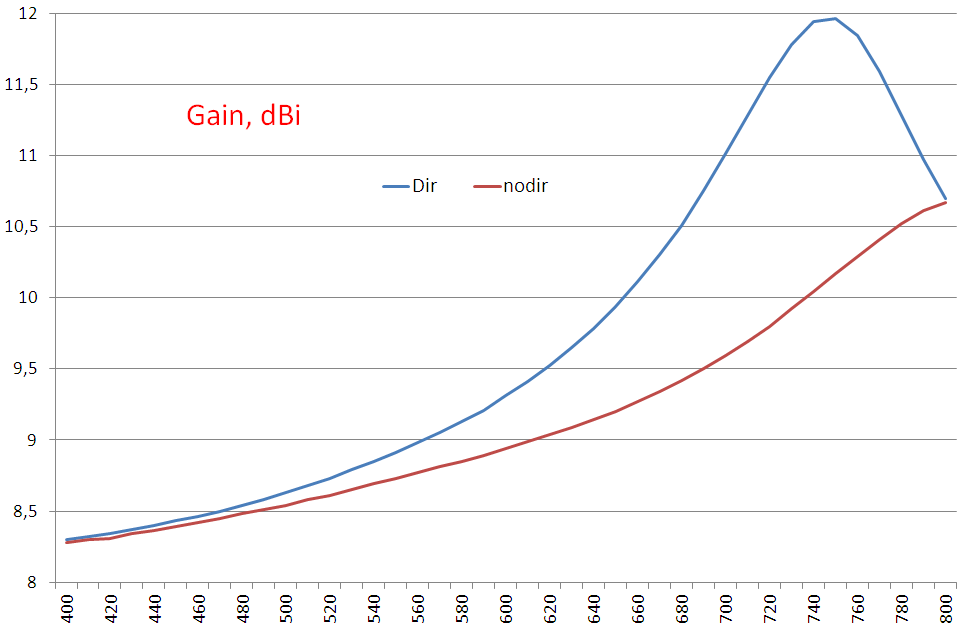






The second director 0.34λ at 0.16λ from the first can give another ~ 0.5 dB gain in the range 550 ... 690 MHz, at the cost of a decrease in SWR by 0.1.
The two-story first director (optimal height is about 0.13λ) gives more growth than the second director.
Screen + 2-Bay Director, Gain, SWR, 3D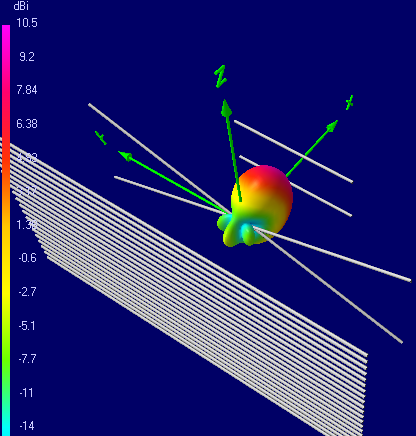



Part IV / Side Reflector
When the width of the main screen canvas reaches 1-1.2λ, a further increase in the screen width no longer gives a significant increase. Further increase in screen width at an angle, i.e. the creation of bent sides, often more profitable than a straight line width. The edges that are optimal for 1λ of the screen are ~ 0.2-0.25λ at an angle of 30 degrees to the canvas.
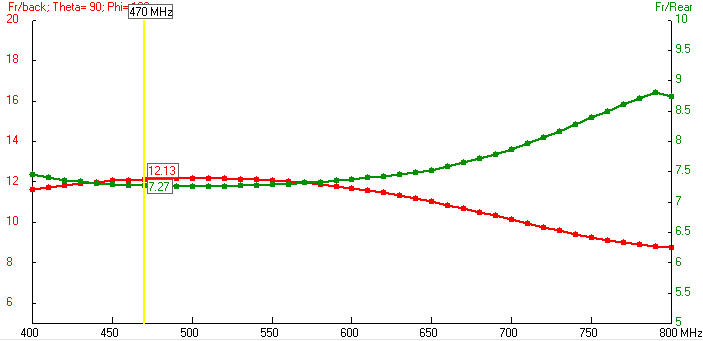
The radiation pattern changes slightly in the horizontal plane - a slight increase (up to 1 dB) of radiation forward, a very significant suppression of radiation backwards, but not by redistributing it forward, but in the rear hemisphere. The ratio of the front and rear hemispheres even deteriorates slightly, but because radiation strictly backward prevailed in the rear hemisphere - to reduce it even by redistribution in the same hemisphere is very beneficial in terms of improving the protective effect of the antenna.
Lips: 3D, pattern, Gain, SWR, F / B & F / R ratio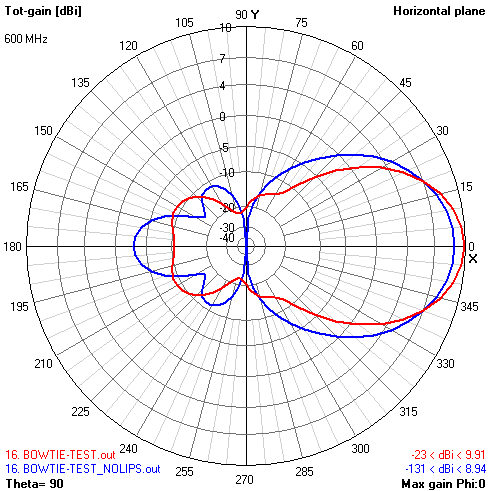

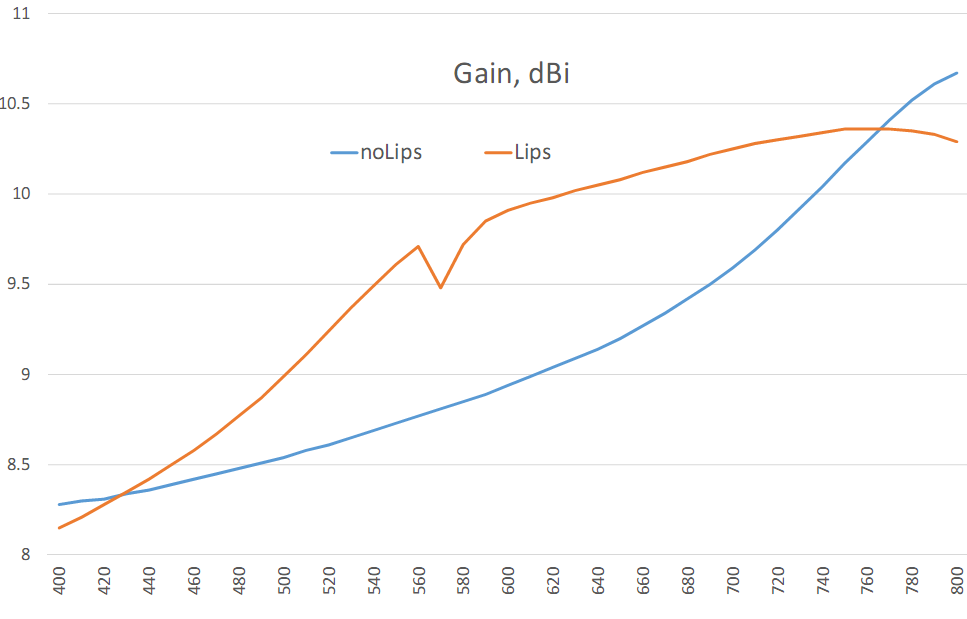
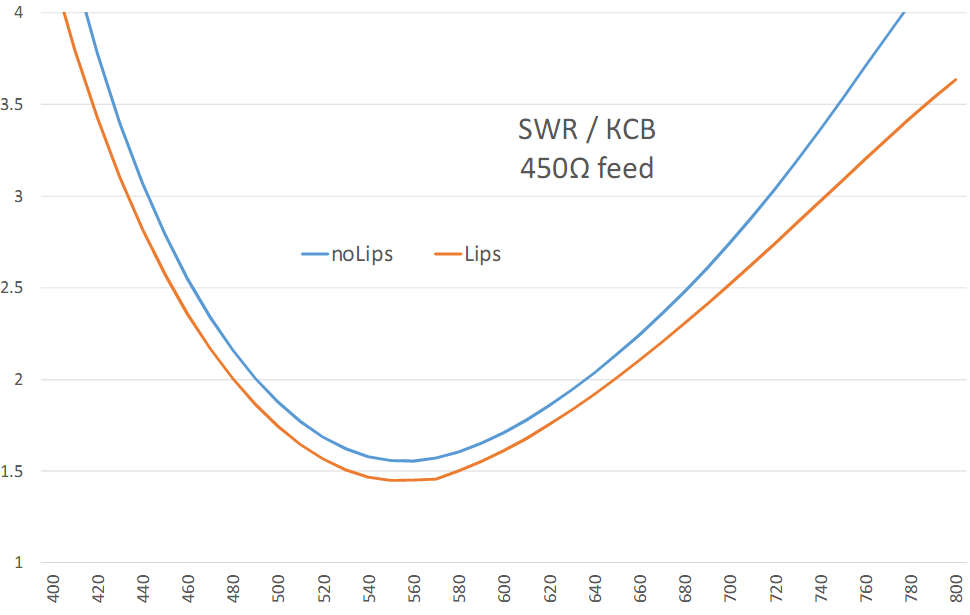
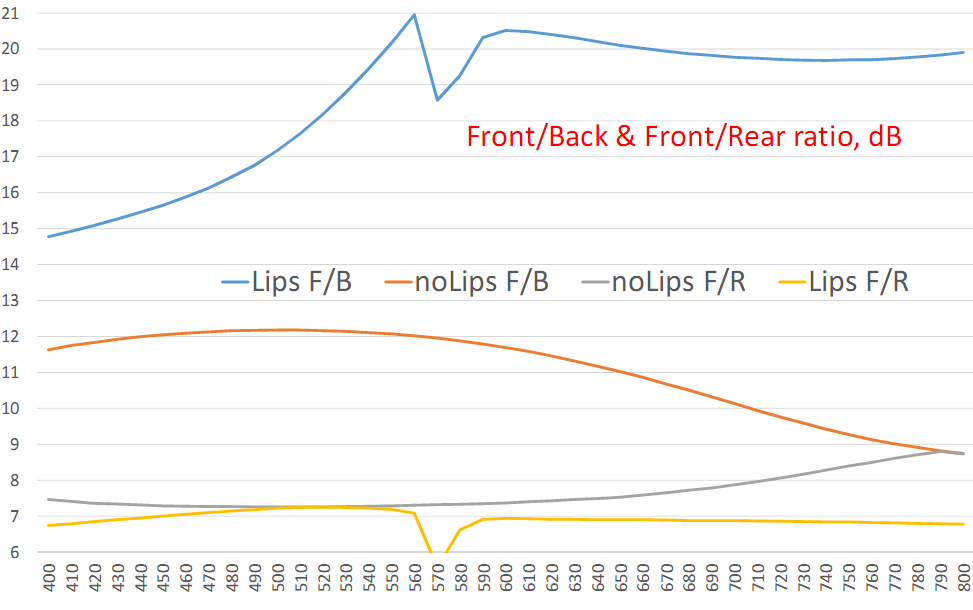





The combination of a screen with side panels and a 2-story director is almost a ceiling that can be pulled out of a single BowTie vibrator. Here is his set of parameters:
Screen 1λ + Lips 0.25λ @ 30 ° + 0.35λ @ H = 0.2λ Director
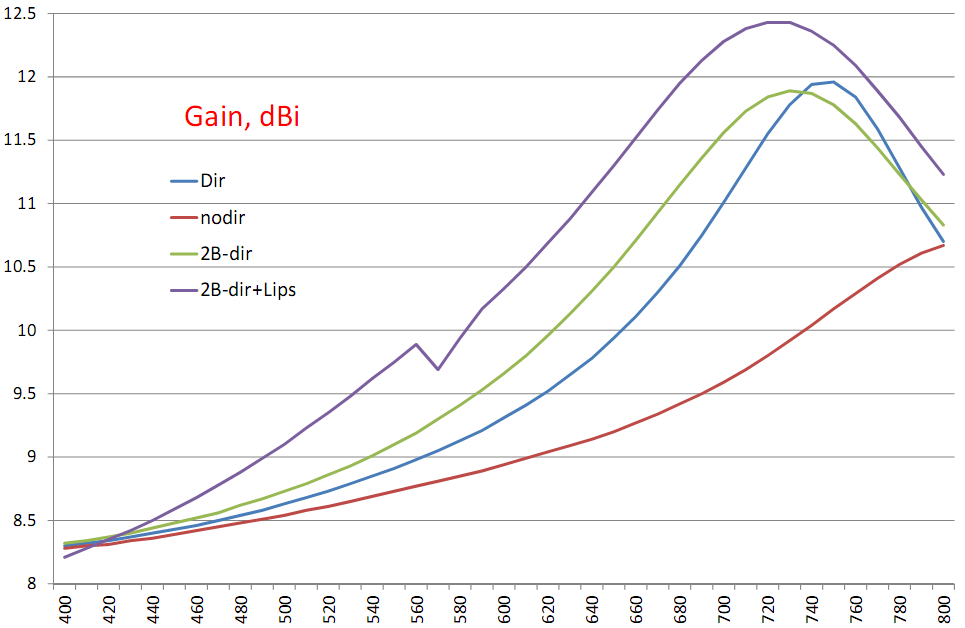





This is how the electric field strength changes in the plane of such an antenna and how far-field radiation is formed from near-field oscillations

Part V / Single Screen Common Mode Gratings
As you can see, the capabilities of a single vibrator are exhausted by a reflector screen. If you want to create an antenna with a narrower radiation pattern and increased gain - it remains only to use several antennas, combining them in phase in one lattice of a larger aperture. For any type of antenna, doubling the number of antennas in the common-mode array can give up to 3 dB gain gain due to narrowing the radiation pattern. The radiation pattern narrows in the plane where we add new antennas. With an increase in the number of storeys of the lattice, the diagram narrows in the vertical plane (becomes pressed to the horizon), while adding new floors to the right or left, in the horizontal plane (beam narrowing in azimuth).
The main obstacle to creating in-phase gratings is technological difficulties. The complexity of the calculation and design increases dramatically, because you must first coordinate each antenna with the transmission line, then add the signals from each pair of lines to a tee, the summing signal again reconcile with the wave impedance of the feeder.
The collection and transmission of a signal from each antenna (each vibrator of the antenna array) can be performed:
* asymmetric (coaxial) line
* symmetric (two-wire) line
Each type of line has its advantages and disadvantages.
Coaxial line:
+ can pass near metal elements and through holes in them
- it is produced on a very limited set of fixed resistances (50 and 75Ω, there are exotic ones at 100 and 150Ω, but it is almost impossible to get them)
- it requires a Bal-Un (Balanced-Unbalanced) balun device to connect to a symmetric vibrator
- additional changes are necessary to the signal phase lines or elements
- the material is only copper, to connect with the structural elements of the vibrator additional elements are needed (for example, soldered terminals)
Two-wire line:
+ can be made for any resistance by selecting the distance or diameter of the wire nicks
+ can be connected directly to symmetrical vibrators
+ can have a structural bearing capacity
+ it is easy to change the signal to antiphase by connecting to the opposite conductor
+ they can be made of any materials, including the vibrator material and even be its constructive continuation, which simplifies the connections
- it is necessary to ensure parallelism, either due to intrinsic rigidity or with the help of dielectric spacers
- can not be placed near metal elements do not cross the magnetic field. metal conductors are especially harmful if they are not equidistant from both lines. During the measurement, the currents flowing in different wires of the line are out of phase and do not cancel each other, which leads to radiation of the feeder.

Structurally, cone antennas coexist very elegantly with two-wire lines with a vertical (multi-storey) layout of the common-mode array.

Using two short (usually shorter than the wavelength) segments of the same length, two signals of equal strength and phase are added together, and a signal is obtained that is 2 times (+3 dB) more powerful than the signal in a single vibrator.
For perfect operation, the wave impedance of the summing line should be the same as that of the vibrator (at this frequency). The output impedance of such a grating will be equal to half the impedance of each vibrator and line.
In a wide frequency range, the vibrator's own impedance varies over a wide range from 85 to 545Ω. The impedance of symmetrical lines does not depend on the frequency, but only on the diameter of the conductors and the distance between them. Therefore, in a wide frequency band, such a line will always be inconsistent. Short mismatched lines (with a length commensurate with the wavelength or less) act as a resistance transformer. This property of such lines is often used for its intended purpose if it is necessary to convert the wave impedance of the lines.
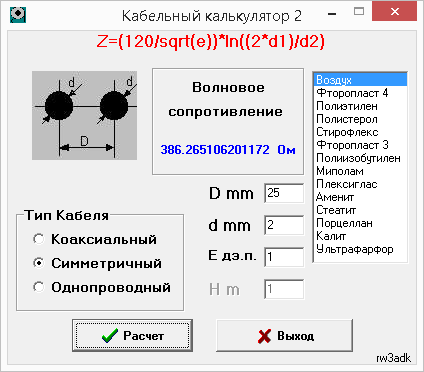
The calculation of the wave impedance of the line is carried out according to the formula or using a ready-made utility .
So, two conductors with a diameter of 2 mm at a distance of 25 mm with an air gap have a resistance of 386Ω
For example, take a short line 0.3λ (looking ahead, we’ll say that it will be half of the optimal floor spacing, i.e. it will be the length of the line from one of the floors to the addition tee on the feeder) and see how it transforms the vibrator’s own radiation resistance in the range frequencies.
One line is 25/2 mm (386Ω), the second is 25/1 mm (469Ω) and the third is twice as long as 25/2 mm (386Ω) for comparison:
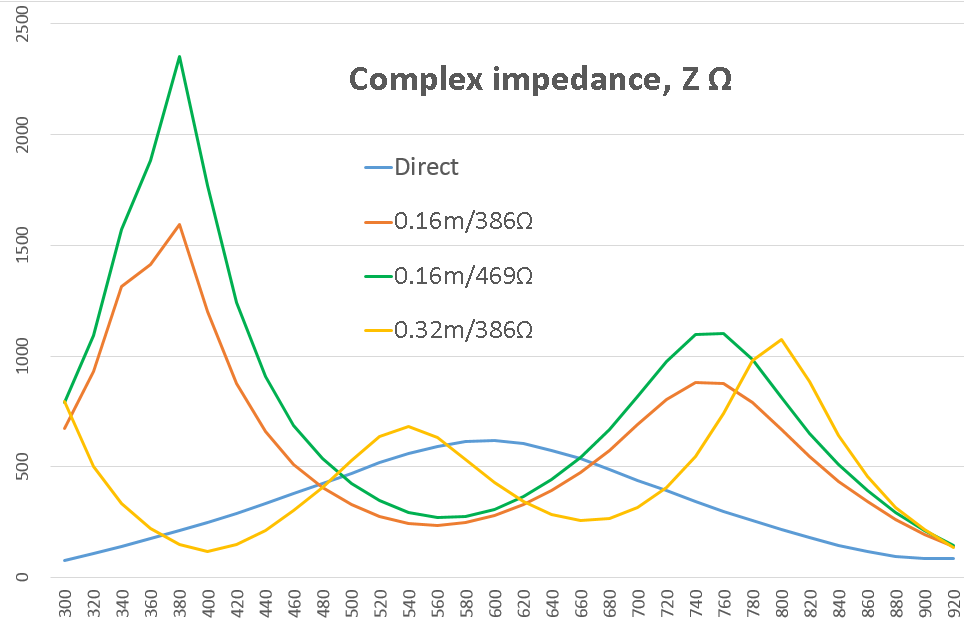
Blue (Direct) indicates the own complex resistance of the BowTie cone vibrator with a direct feeder connection.
As you can see, the collecting line has a very strong effect on the resulting impedance. Moreover, the transformation coefficient is less dependent on the resistance of the transformer, but more on its length (correlated with the wavelength). Because for different frequencies, the same transformer section represents a very different length.
To calculate this resistance, there is a formula
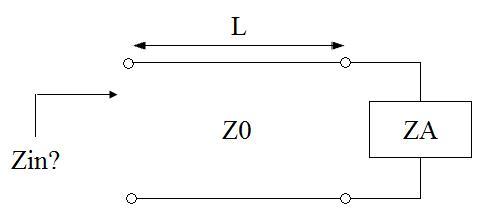

When ZA = Z0, then Zin = Z0. A source matched line does not change the resulting impedance.
In other cases, Z0 is multiplied by a coefficient that depends on f * L (i.e., on the wavelength) and depends on ZA and ZO
The length of the collecting lines in the common-mode array can theoretically be any (if only equal so that the signals arrive in-phase and add up), but from technological motives it is rational to carry them out in the shortest way, connecting the floors in a straight line. With this approach, the line length will be set based on the optimal distance between floors, and coordination will only have to be improved by varying the line resistance: changing the diameter of the conductors or the distance between them.
When building 3 or more floors, it is technologically very impractical to carry out independent lines from each next floor to the adder. Fortunately, you can add the signal from the neighboring floors directly to the neighbor's terminals. Because Since the floors are located approximately at a length of 1 / 2λ between themselves, then when passing along a collecting line with a length of 1 / 2λ, the phase of the signal changes by 180 degrees to the opposite. In order for such signals to be summarized, rather than mutually destroyed, it is necessary to connect the conductors in antiphase. All floors are connected to each other only in antiphase, with overlapping lines. The exception is the grid feed point (feeder, balun), as It is located at an equal distance from the floors (not necessarily in the shortest way), then the signal on it will be in-phase when connected not directly with the overlap, but.
The shape of the directivity pattern (MD) of the in-phase antenna array is determined by the antenna array constituting the array and the configuration of the array itself (number of rows, number of floors and the distance between them).
With two omnidirectional antennas placed side by side at 1/2 λ (between the axes of the antennas), the horizontal beam looks like a figure eight, and there is no reception from the lateral directions perpendicular to the main one. If you increase the distance between the antennas, the width of the main lobe of the radiation pattern decreases, but side lobes appear with maxima in directions perpendicular to the main one.
At a distance of 0.6λ, the level of the side lobes is 0.31 of the level of the main lobe, and the width of the beam at half power decreases by 1.2 times relative to the array with a distance between antennas of 2/2.
At a distance of 0.75λ, the level of the side lobes increases to 0.71 of the main level, and the width of the beam decreases by 1.5 times. At a distance of 1λ, the level of the side lobes reaches the level of the main lobe, but the width of the radiation pattern decreases by 2 times compared to the distance between the antennas in half-wavelength.
This example shows that it is more advisable to choose the distance between the antennas equal to the wavelength. This provides the greatest narrowing of the main lobe of the radiation pattern. There is no need to be afraid of the presence of side lobes, since when using directional antennas as part of the array, they do not receive signals from directions perpendicular to the main one.
These are general guidelines for any type of antenna. So antennas are usually mounted when they are added through a coaxial cable. The pieces of flexible cable of arbitrary (if only the same) length are stacked arbitrarily. Changing the distance between the antennas does not violate the coordination and summing, so you can choose any distance from 0.5 to 1λ.
Consider the specific grating pattern of 2 BowTie vibrators with a reflector, depending on the spacing between floors.
2-Bay radiation pattern for 0.4 - 1λ vertical stack

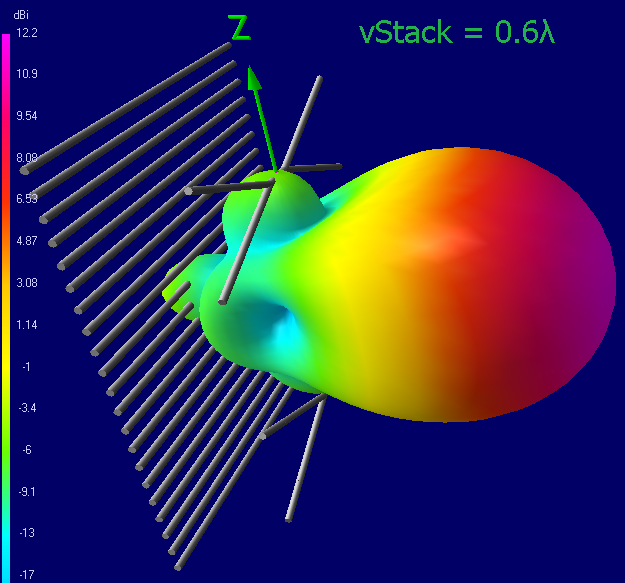
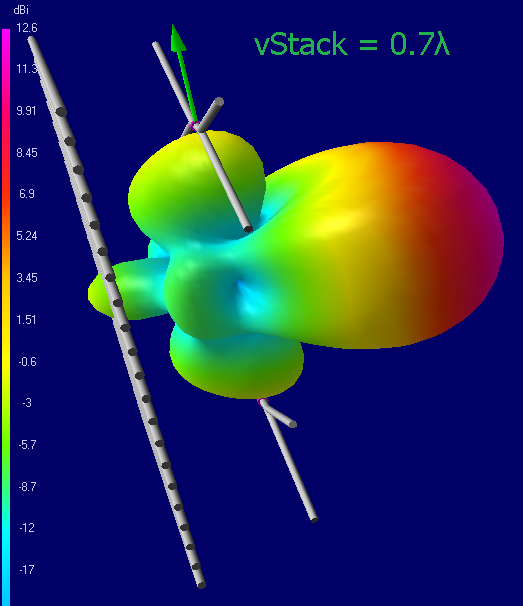
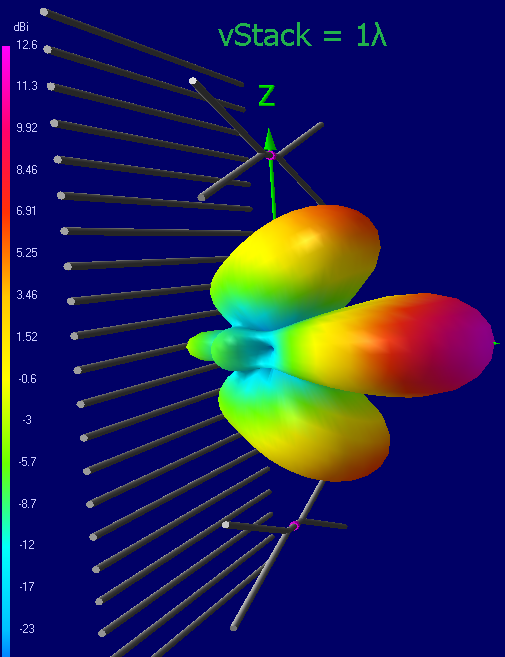





As you can see, with an increase in separation, the gain increases from 11 dBi@0.4λ to 12.6@0.6λ.
With a separation of more than 0.6λ, the gain of the main lobe does not increase, but it becomes narrower in the vertical, and due to this, two parasitic lobes grow up and way down. Although formally the gain of the antennas 0.6-1λ is the same, a narrower lobe requires more careful orientation of the antenna to the subscriber (usually to the horizon)
For a 2-storey array of cone antennas, you can choose any distance from 0.4 to 1λ. But with an increase in separation in excess of 0.6λ, the screen size and the length of the bearing beam also increase, i.e. material consumption increases, weight and strength deteriorates, without an increase in parameters.
In addition, as we have already seen, an increase in the length of an inconsistent collecting line significantly affects its transformation coefficient. Therefore, for practical reasons, 2-story gratings are designed with a minimum spacing of 0.5-0.6λ.
For 3 or more floors, it is irrational to collect signals using individual lines (they should be between the vibrator and the reflector, away from metal objects) from each floor to the tee, and it is structurally much easier to sum the adjacent floors directly to the vibrator. If the distance is not a multiple of 0.5λ, then the signal delay in the line will not be a multiple of 180 degrees and the signals will not add up in phase. Therefore, for a direct connection along the shortest path, a spacing of only 0.5 or 1λ is suitable. At 0.5λ, the lines should overlap (for phase rotation by 180 degrees), at 1λ directly (without phase rotation). For practical reasons described for a 2-story grating, the spacing 1λ is not applicable.
Part VI / Coordination using a resistance transformer
Three types of structures are used to convert the antenna resistance to the feeder resistance:
1) Broadband transformers with a fixed conversion coefficient. They are usually performed on ferrite cores or printed on microstrip (patch) lines. The transformation coefficient is determined by the configuration of the windings and the ratio of the number of turns in them.
2) A wide variety of shunt circuits with L and C elements.
3) Transformers using wavelength segments
The disadvantage of broadband transformers is the cost of their manufacture and the difficulty of obtaining multiple (arbitrary) transformation ratios. Low cost can only be obtained by mass production, which means a limited range. De facto affordable can only be called 4: 1 baluns. The need to produce a balun at a different factor (6: 1, 8: 1) puts an end to both serial production and home-made products.
The disadvantage of shunt circuits is the complexity of manufacturing (as with non-standard baluns), narrow bandwidth and the need to fine-tune the sample for devices.
The segments of the wave lines do not greatly complicate the design of the vibrator (may be its constructive continuation), simplify the technological installation of the box with the balun (or the combined Balun + LNA board) due to the removal of the box beyond the gap of the vibrator. They can be designed and manufactured to convert almost any resistance into any selection of the length of the segment and its own resistance.
Let us consider in more detail the fundamental formula for the transformation of resistances given in the previous section. A
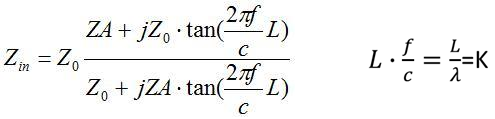
number of observations follow from this formula:
- With a line length of 0 or a multiple of 1 / 2λ, the resulting resistance is equal to the resistance of the source, the line does not change the impedance, because the tangent of angles of 180 is zero
- При длине линии со сдвигом 1/4λ от кратных 1/2λ — результирующее сопротивление изменяется максимально, потому что тангенс углов 90 и 270 стремится к бесконечности
- Линия с сопротивлением равным сопротивлению источника (согласованная) не вносит изменения в результирующий имепаданс при любой длине линии
- Линия фиксированной геометрической длины будет вести себя по разному в широкой полосе частот при изменении длины волны. Если с изменением частоты длина линии в лямбдах приближается к 0 или кратна 1/2λ, то вклад линии снижается, если длина приближается к 1/4λ — вклад линии резко растет. Это свойство потенциально можно использовать для выравнивания собственного импеданса вибратора
Let's create an Excel to work with this formula: goo.gl/w8z9U2 (Google Docs)
Let's say our BowTie vibrator has a resistance of Z = 750 + j0 at the frequency of the first resonance.
To convert 750 Ohms to 300 (for connecting to a 4: 1 balloon), you can use a symmetric waveguide with a length of only 0.1λ (5 cm for a frequency of 600 MHz) with a resistance of 231 Ohms.
Using the coax_calc calculator above, you can choose a combination of the diameter of the wires and the distance between them to get 231 ohms.
Part VII / Case Studies
The scope of cone antennas is very limited. At frequencies below 300 MHz, such antennas are unacceptably large compared to a half-wave dipole, which has a magnitude of 0.5λ versus 1λ.
At frequencies above 800 MHz, there are almost no radio technologies where highly directional antennas are needed. CDMA, GSM, GPS, LTE, WiFi need either omnidirectional antennas at the subscriber, or sector antennas with a clearly predictable sector shape on the operator's side.
A small demand for highly directional antennas exists among fixed-line cellular subscribers. Using BowTie radiators, it is theoretically possible to manufacture LTE-700, CDMA2000 / LTE 800 Mhz, GSM / UMTS / LTE-900 antennas and CDMA2000 / LTE 450 Mhz antennas. The industry did not produce such antennas, but in Part VIIIwe will try to design such an antenna, at the same time checking how efficient and competitive such a design is.
At frequencies above 2 GHz, cone antennas can only be printed (microstrip), there are no advantages in parameters or the simplicity of design and manufacture compared to patch antennas at such frequencies.
In the range between 300 and 800 MHz, only broadcasting works: PAL / SECAM / NTSC (analog) or DVB-T / T2 / T2 HD (digital).
It was the market for TV broadcast subscriber antennas that brought cone antennas unprecedented popularity.
In the 1960s, such antennas acquired most of the market in geographically large countries: Canada and the United States. Large areas, mainly flat, caused a lower density of construction of TV towers compared to Europe. At large radii of coverage, high gain antennas of 10 ... 16 dB were required. To achieve such amplification from single antennas, the wave channel is very problematic, and using in-phase arrays of 2-4 antennas, the wave channel is difficult and expensive, compared to the simplicity of a multi-storey cone antenna with a reflector.
The widest distribution of such antennas in Eastern Europe was facilitated by the appearance of a large number of low-power TV channels in the UHF range (1-5 kW compared to 20-25 kW for three central television channels), for the reception of which antennas with a gain of 10+ dB, as well as broadband are needed with capturing (albeit with low gain) sections of the MV range, which made it unnecessary to contain an additional antenna of the MV range, additional cables, amplifiers, adders, etc.
We present to the reader 7 antenna designs that have been carefully optimized (using Python scripts using the NEC-engine for modeling) to maximize the average gain in the range 470-700 MHz (21-50 channels DMV) and minimize the average SWR (SWR). For 2017, such antennas are relevant only for DVB-T / T2 reception.
Without reflector:
1) 2-Bay: 50x55 cm, mustache 8x279 mm
2) 3-Bay: 60x50 cm, mustache 12x241 mm
3) 3-Bay (1 small): 80x65 cm, mustache 4x276, 4x302 and 4x190 mm
With reflector / screen:
4) 1-Bay: 25x72 cm (50 + 2x12.5 cm sides), mustache 4x222 mm (from the example in the article)
5) 2-Bay: 86x57 cm, mustache 4x254 mm
6) 4-Bay: 102x86 cm
7 ) 6-Bay: 152x84 cm
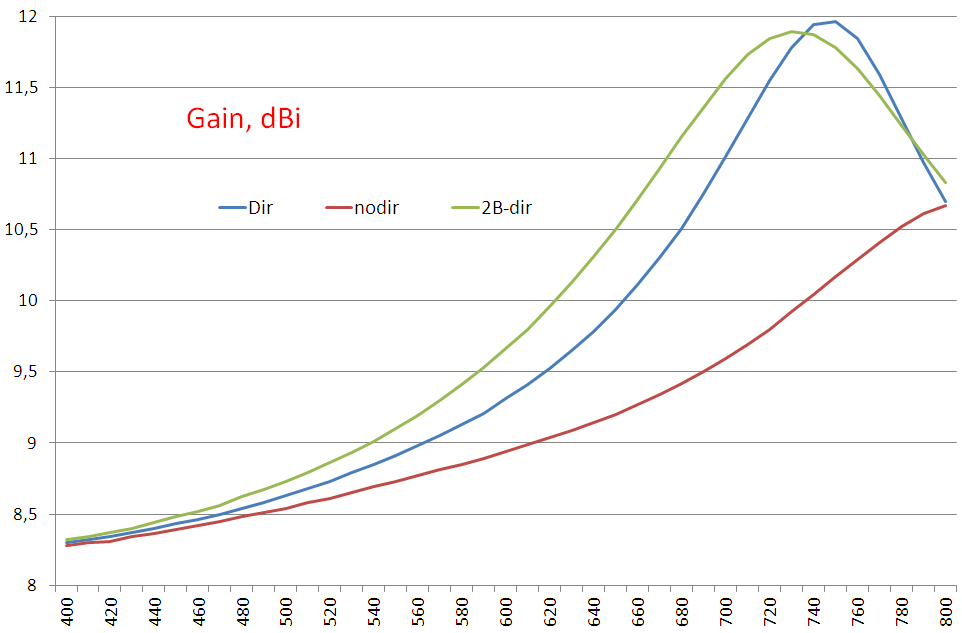
Gain, SWR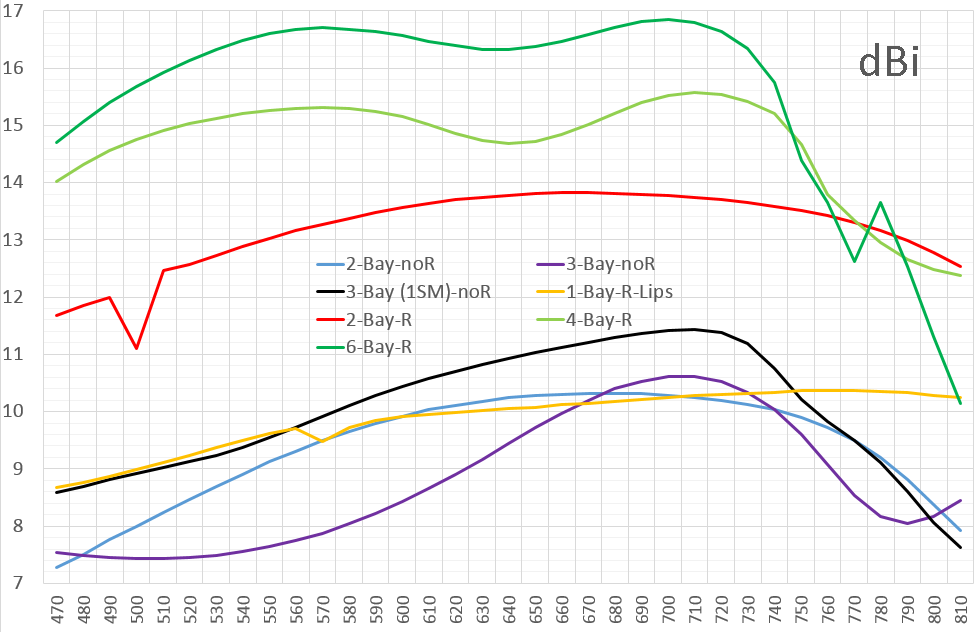



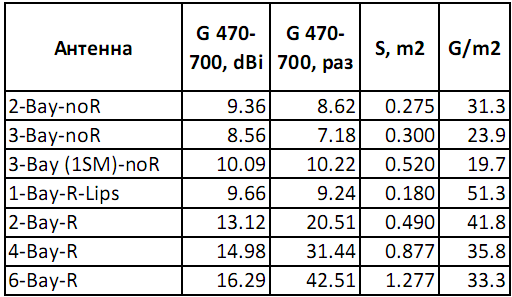
The antenna gain averaged over the band 470-700 MHz is 7 to 42 times or 8.5 to 16.3 dBi.
The third column shows the area of the frontal projection in m2, and in the last - the specific gain, at times per 1 m2 of the frontal area.
For comparison, the wave channel antenna (Uda-Yagi), specially optimized for the same range, has an average gain of 10 dBi (from 8.1 to 12.1) in the 1R-5D configuration (1 reflector, 5 directors, loop vibrator, 624x293x45 mm) and 12.7 dBi in 2R-15D configuration (2 reflectors, 15 directors, loop vibrator, L = 1621 mm)
Conclusions:when designing antennas with an average gain of up to 10 dBi, traditional dipole antennas the wave channel is simpler, more compact, lighter, easier to manufacture (both artisanal and industrial) and more durable. If amplification> 10 dBi is required, then adding directors to the Uda-Yagi adds very little directivity (1R5D = 10 dBi, 2R10D = 11.5 dBi, 2R15D = 12.7 dBi), while even a 2-story cone antenna with reflector gives an average gain of 13.1 dBi .
When an average gain of 15-16 dBi is required, there is no alternative to 4 and 6-story cone antennas. In the segment of antennas with a gain of 10-13 dB, a 2-story cone antenna is more compact and simpler than long wave channels with 10 or more directors).
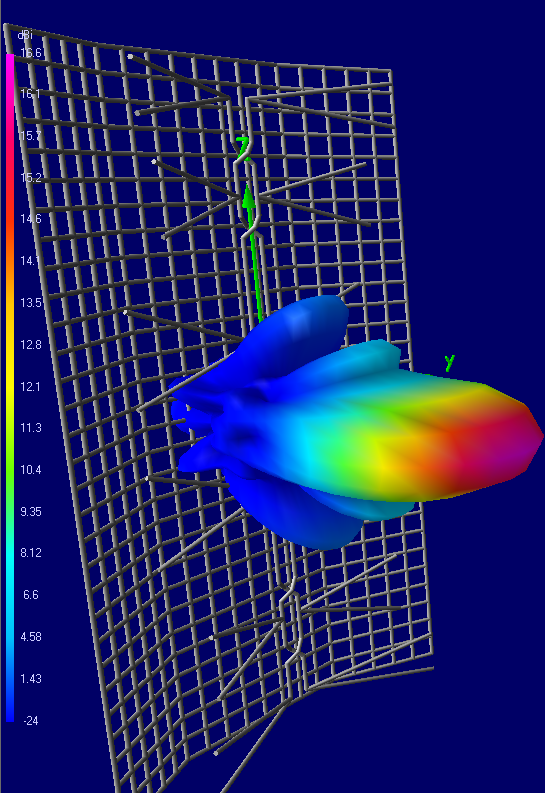
Here is a general view and the DN of the seven antennas, in the order numbered above:
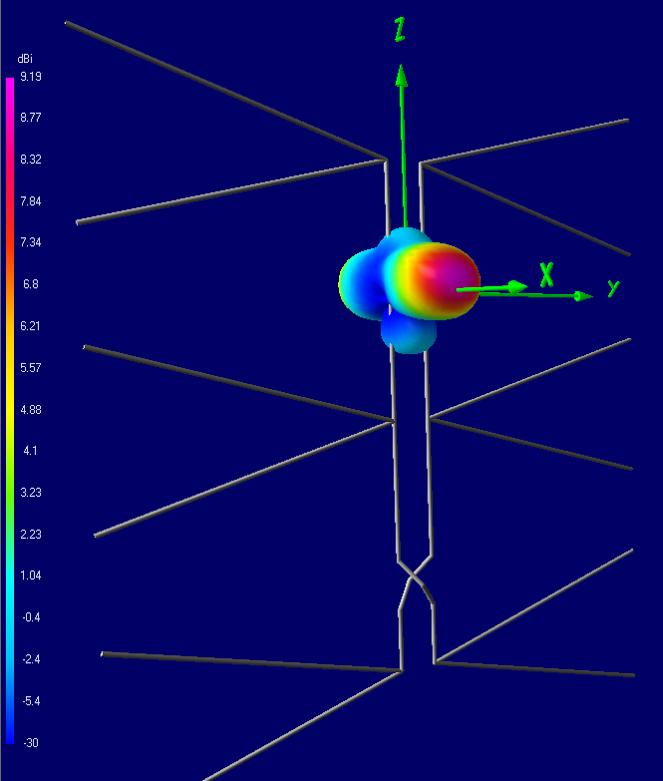
3D View, Pattern @ 600 MHz
1) 2-Bay: 50x55 cm, mustache 8x279 mm
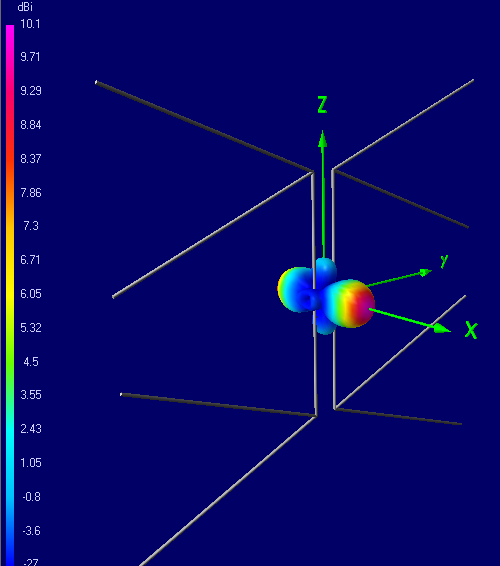
2) 3-Bay: 60x50 cm, mustache 12x241 mm
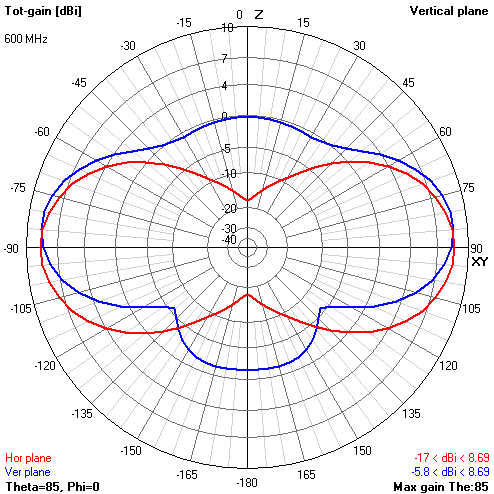
3) 3-Bay (1 small): 80x65 cm, mustache 4x276, 4x302 and 4x190 mm
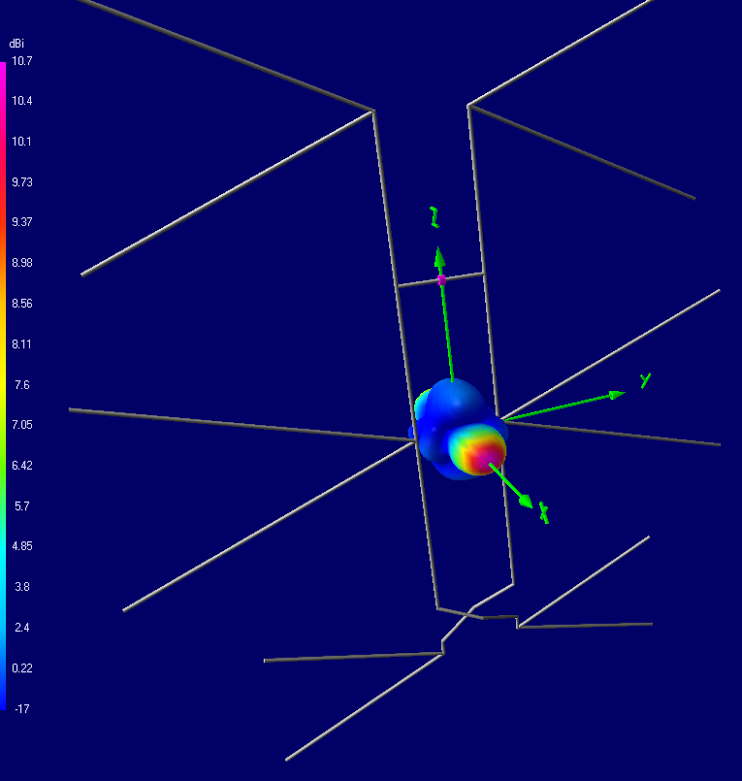

4) 1-Bay: 25x72 cm (50 + 2x12.5 cm sides), mustache 4x222 mm (from the example in the article)


5) 2-Bay: 86x57 cm, mustache 4x254 mm
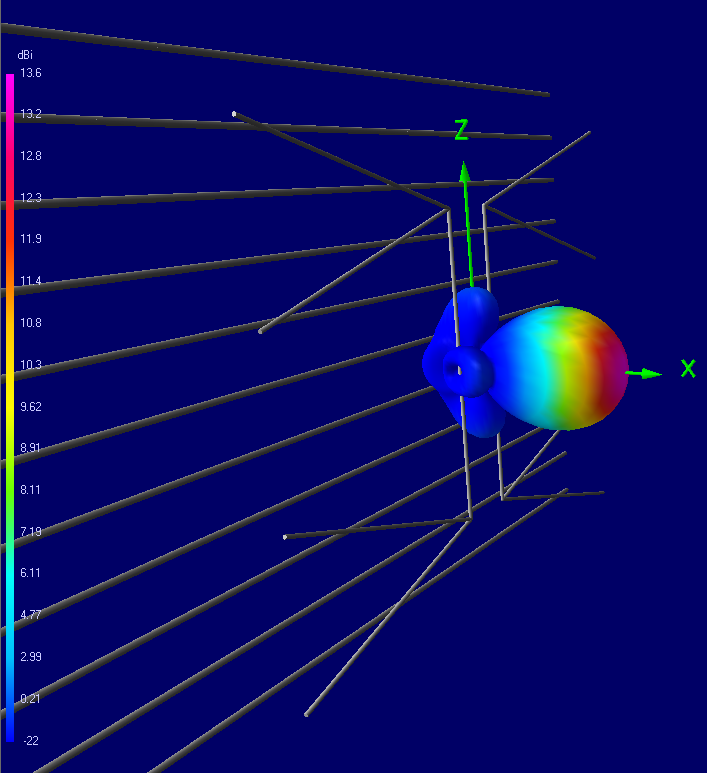

6) 4-Bay: 102x86 cm
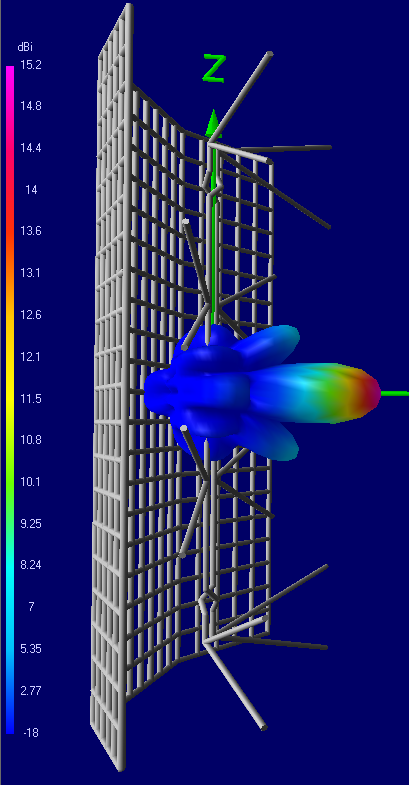
7) 6-Bay: 152x84 cm



2) 3-Bay: 60x50 cm, mustache 12x241 mm


3) 3-Bay (1 small): 80x65 cm, mustache 4x276, 4x302 and 4x190 mm


4) 1-Bay: 25x72 cm (50 + 2x12.5 cm sides), mustache 4x222 mm (from the example in the article)


5) 2-Bay: 86x57 cm, mustache 4x254 mm


6) 4-Bay: 102x86 cm


7) 6-Bay: 152x84 cm


All 7 models in * .NEC format can be downloaded here and see detailed sizes (including creating executive drawings) using the free 4NEC2 program .
Disclaimer : The 6 presented UHF-TV antennas were developed by DigitalHome Canada forum members led by holl_ands and mclapp users .
Part VIII / Industrial Design Analysis of the Antenna
4-storey antennas such as ASP-8 have gained widespread popularity in the CIS.
These antennas have many modifications that differ slightly from each other (in the details).
Older antennas had longer upper floor whiskers (and were labeled as 47-860 MHz antennas).
The new antennas (which are sold in 2017) have a slightly shorter upper floor than the old ones, probably for better performance in the UHF, where DVB-T / DVB-T2 is currently operating.
For analysis, the dimensions were taken from such a sample at a cost of $ 3.6 (at a price - like a 3-element room Yagi Wave-1)
The antenna has the following elements:
1) A reflector screen 75x50 cm, 36 cm the width of the central part, side panels 2x8 cm are bent 4.5 cm forward.
The screen consists of 2x6 horizontal conductors with a diameter of 2.1 mm, each of the two groups has a height of 33 cm, and between them (in the central part of the antenna) there is a gap of 9 cm.
Offset of the screen from the vibrators is 85 mm
2) The gap between the mustache of the vibrators on all 4 floors 34 mm (at the center of the waveguide lines)
3) The upper vibrator 4x254 mm mustache with a diameter of 5 mm, with an opening angle of 45 degrees
4) The three lower floors - vibrators 4x140 mm mustache with a diameter of 4 mm, with an opening angle of 50 degrees
5) A collecting two-wire line of steel conductors with a diameter of 2.1 mm, the distance between the conductors is 34 mm at the points of entry to the mount of the vibrator. At the entrance to the power box 30 mm from the bottom and up to 72 mm from the top.
6) The distance between the floors (1st - upper): 1-2 = 183 mm, 2-3 = 192 mm, 3-4 = 178 mm
7) The length of the connecting lines: 200 mm between 1-2 and 3-4. 84 + 132 = 223 mm between floors 2-3. The power box terminals are 84 mm from the top and 132 mm from the bottom floor.
8) On each floor there is a traverse with 5 short directors.
9) The antenna ridge - an aluminum hollow profile 12x6 mm at a distance of 28 mm behind the waveguides
We must say right away that traverses with 5 directors have no influence whatsoever on the antenna at frequencies up to 900 MHz. At frequencies above 800 MHz, they add only +0.1 dB to the directivity.
Their function - exclusively decorative - is to destroy the antenna with additional mechanical loads and to attract birds to destroy the antenna.
Imagine the main components of the geometry of the antenna at wavelengths, in different parts of the claimed range of operation

The dimensions of all the elements of this antenna are extremely strange: the length of the whiskers, the spacing between the floors, the width of the reflector, the deliberate displacement (dephasing) of the power supply point.
Consider the properties of individual vibrators (taking into account the effect of the screen).
Bay-1 : The top long vibrator has a resonant frequency of 490 MHz and a resistance of 850Ω. The second resonance at 780 MHz and a resistance of 31Ω. At frequencies below 300-320 MHz, the radiation resistance R is negligible, we can assume that 320 MHz is the lower working frequency. The gain of this floor alone reaches 10 dBi, but the radiation pattern is slightly (1 dB) shifted down 30 degrees, like a Bay-2 hanging belly
: The second top vibrator has a resonant frequency of 780 MHz and a resistance of 515Ω. The second resonance lies above 1000 MHz. At frequencies below 460 MHz, the radiation resistance R is negligible, we can assume that 460 MHz is the lower operating frequency. The gain of this floor alone reaches 11 dBi, but the radiation pattern is STRONGLY shifted downward by 35 degrees. The gain forward is only 6 dBi, and down 35 degrees to 11.1 dBi
Bay-3 : The third vibrator from above has a resonant frequency of 790 MHz and a resistance of 620Ω. The second resonance lies above 1000 MHz. At frequencies below 440 MHz, the radiation resistance R is scanty, we can assume that 440 MHz is the lower working frequency. The gain of this floor alone reaches 10.6 dBi, the shape of the beam is not distorted, but Bay-4 looks forward
: The bottom vibrator has a resonant frequency of 810 MHz and a resistance of 570Ω. The second resonance lies above 1000 MHz. At frequencies below 440 MHz, the radiation resistance R is scanty, we can assume that 440 MHz is the lower working frequency. The gain of this floor alone reaches 9.6 dBi, the shape of the beam is distorted upward by 20 degrees (2-3 dB stronger than forward). The second directional bubble is directed down 30 degrees.
The manufacturer made a very strange choice of the length of 3 whiskers on 3 floors - with a resonance near 800 MHz, and not in the middle of the UHF range (in the range of 600 ... 700 MHz).
Also a very strange choice of floor spacing and collective line lengths. The length of the waveguides that overlap is centered at 750 MHz. At a frequency of 470 MHz, the phase delay in such a line is 112 instead of 180 degrees.
ASP-8, 3D, Gain, SWR, Pattern















As you can see, the antenna parameters are very unstable in a wide band of the claimed frequency range. In some sections, SWR matching <2 (acceptable), in some SWR = 2 ... 3.2 (acceptable when loaded on the LNA, otherwise attenuation increases sharply in the drop cable), and SWR = 3.6 on channel 21 (470 MHz)
Diagram directivity is also unstable and has local anomalies. This instance has an anomaly of 565 MHz (+ 30 / -40 MHz) - the beam falls apart up and down, the radiation is forward only 5 dBi.
Previously, these antennas were positioned as MV + UHF antennas of 47-860 MHz.
In fact, this statement is a gross lie. At frequencies below 220 MHz, the antenna gain is negative.
As we learned from theory, when the length of the parasite is less than 0.47λ, it turns from a reflector into a director, because DN is shifted towards this “reflector”, i.e. in the opposite direction from the TV tower. In the direction of the TV tower, the signal is attenuated 10-16 times in comparison with a half-wave dipole.
ASP-8 @ HiVHF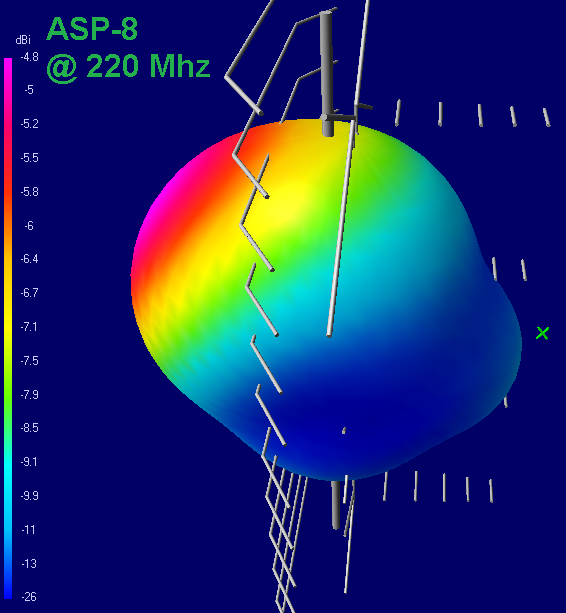

In addition to this freak antenna, we also analyze the ChannelMaster 4251 antenna from 2 floors, which is popular in North America.
Its dimensions are much smaller: 38x35 cm (against 75x50 cm)
CM4251, Gain, SWR, 3D




The gain increases smoothly from 8 to 10 dBi, the shape of the beam is perfectly flat, and the SWR is moderate. There are no resonant anomalies between 400 and 900 MHz.
CM4251 with a frontal projection 2.8 times smaller than that of ASP-8, works in much the same way, but without abnormal parts of the frequency response and without surges.
Both antennas are significantly inferior to the 2-story antenna from an article optimized using CAD.
The optimal dimensions for 2 floors - 86x57 cm (86 - width), this screen is slightly larger than the "Polish dryer", but turned to the side.
Attempts to fit 4 floors on such an area are very unsuccessful and are only marketing in nature.
The American version, although it does not have outstanding amplification, is small in size.
Part XIX / Calculation of a highly directional transmit-receive antenna
A conical radiator with a reflector allows theoretically producing antennas with amplification of the order of 10 dBi for 1 floor, 12-13 dBi for 2 floors, 14-16 dBi for 4 floors, 16-18 dBi for 6 floors.
When working with horizontal polarization, the common-mode array will have a vertical layout. At 2 floors, the directivity pattern will be the same both vertically and horizontally: attenuation of 3 dB at angles of ± 25 in any direction from the main beam.
At 4 and 6 floors, the azimuth selectivity does not change, and the beam becomes very narrow vertically, so at 16 dBi the attenuation of 3 dB is already at ± 8 degrees vertically.
A distinctive feature of transceiving antennas from purely receiving (television) antennas are:
- feeder resistance 50Ω
- increased requirements for low SWR
Purely receiving antennas are more tolerant to mismatch (high SWR) because cable losses (including additional losses from high SWR) can be leveled by installing LNA directly into the antenna on the vibrator terminals.
The loss of signal power at the entrance to the LNA is usually estimated by the equivalent increase in the noise factor (SNR degradation) from the mismatch.
From the formula,
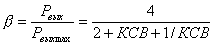
we obtain the formula
Nf (effective) = Nf (nominal) + 10 * log ((2 + SWR + 1 / SWR) / 4)
SWR = 2 and SWR = 3 is equivalent to a decrease in the noise factor LNA by 0.5 and 1.25 dB, respectively.
SWR transmitters are considered acceptable for SWRs <2, and good SWR <1.5.
Using the theoretical knowledge from the previous chapters, we will try to calculate a 2-storey common-mode array with good SWR for a load of 50Ω.
As an example, we choose the range 821-894 MHz (858 ± 37 MHz), in which the CDMA2000 / EV-DO standard works.
We will calculate the antenna for operation at frequencies close to resonant, because with a large imaginary part of the complex resistance, the SWR will be far from 1 even if the feeder is matched with the complex resistance.
The actual radiation resistance ® of the cone vibrator, as we already know, is of the order of 400-1000Ω and depends on three main factors:
- diameter of the vibrator conductor (strong inverse relationship, the thicker the conductor the lower R)
- distance to the reflector (strong direct relationship, than further from the screen, the higher R is)
- the presence of a number of other lattice vibrators (weak dependence)
This order of magnitude of R is very far from 50Ω, so the use of a resistance transformer is inevitable.
Even if R = 50Ω, it is still necessary to use Bal-Un 1: 1, because The BowTie vibrator is balanced, and the coaxial power cable is asymmetrical.
The easiest way to use a combined BalUn transformer.
When using a 4: 1 transformer, it is necessary to calculate the antenna with an output of 200Ω, when using a transformer 6: 1 - by 300Ω.
When adding a signal from 2 floors to a tee, the output resistance of the grating is 2 times less than the resistance of the floors. Those. a single vibrator must be calculated at 400Ω or 600Ω.
Collector lines should have the same resistance as a single vibrator, i.e. 400Ω or 600Ω, otherwise they will work as transformers with unpredictable effect.
Using the coax_calc program, we will try to simulate a symmetrical waveguide at 400Ω and 600Ω.
To get 600Ω, even with a thin conductor d = 1 mm, a separation of 74-75 mm is needed. This is a fairly large spacing (relative to the total width of the vibrator of the order of 25-30 cm), and a rather thin (non-rigid) conductor. For such a large spacing, the protective zone also increases, where there should be no metal objects.
To get 400Ω, the dimensions of the line are quite convenient: 35 mm spacing, with a wire d = 2.5 mm (5 mm2 wire common in electrics)
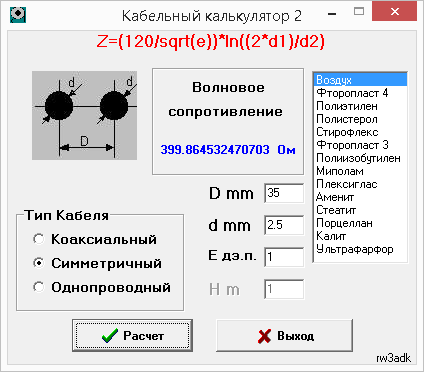
The 400Ω option is also more convenient, because 4: 1 baluns are widely distributed at a penny cost, and a 6: 1 balun will have to be specially made.
We begin the calculation with a screen with a width of 1λ at the center frequency (349 mm for 858 MHz)
To reduce the resistance R to 400Ω, you need to take the thickest conductor for the vibrator as possible, or remove the vibrator from the screen. For technological convenience, we select the diameter of the mustache conductor 6 mm (the upper mustache in the “Polish dryer” has such a diameter). With a length of whiskers of the order of 13-15 cm, they will have sufficient rigidity. Thicker tubes of the order of 10 mm will be both more expensive and less convenient to bend and mount.
We create a geometric model of the antenna, which includes:
- 1x1λ screen (of 21 horizontal conductors, with a diameter of 2 mm, as in a construction galvanized wire mesh, in 0.05λ increments)
- a gap between the vibrator mustache 35 mm
- a mustache vibrator with a diameter of 6 mm, and its mirror copy at a distance of 0.6λ (± 0.3 λ from the center of the screen)
- the opening angle of the whiskers is 33 degrees.
In several iterations, we select the offset from the screen to get R = 400Ω at the center frequency (858 MHz), and we select the length of the mustache after each iteration to get X = 0Ω (make the imaginary part of the resistance 0, i.e. to tune the antenna to resonance)
after 2-3 iterations obtain lengths whiskers 0.4442λ (138.5 mm), the displacement of the reflector to 0.2455λ (86 mm)
We check the impedance (R, Z), SWR in a wide frequency range (so far without waveguides, with virtual power supply of the vibrators with two sources of 400Ω each).
3D, Pattern, SWR

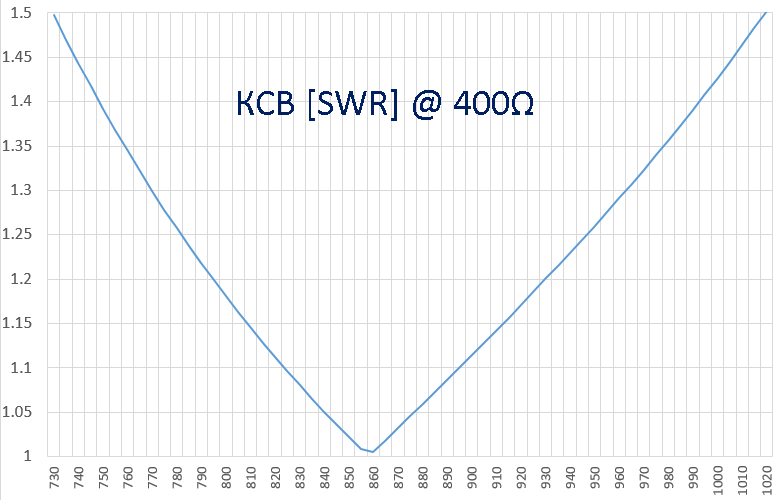



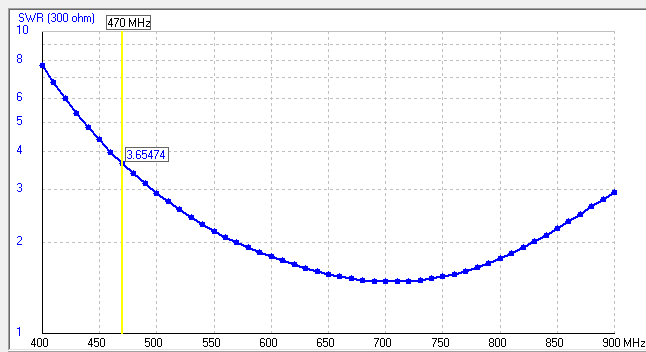
As you can see, the coordination in a wide range of frequencies turned out to be excellent: SWR <1.5 in the range 730 ... 1020 MHz, full width 290 MHz or ± 18%
In the required frequency range 821-894 MHz, SWR ≤1.11
The radiation pattern is flat, gain from 11.8 up to 12.4 dBi
For comparison, the BiQuad antenna (Kharchenko) with the same 1x1λ reflector (without sides) has a gain of 10.6-10.8 dBi and an SWR of up to 1.52 from the bottom and 1.86 from the top of the range.




