Using NES game research tools as an example of parsing the compression format of the Felix The Cat game
In this article, I’ll show you how to use the Felix The Cat for NES game research tools described in a previous article . My initial goal was, as usual, to parse the format of the game levels and add it to my universal CadEditor level editor , however, during the study of the game it turned out that the level description was compressed (this is rare for NES games!), So I also sorted out the data compression format , and wrote a compressor that allows you to compress edited levels in the same way as the game developers did.
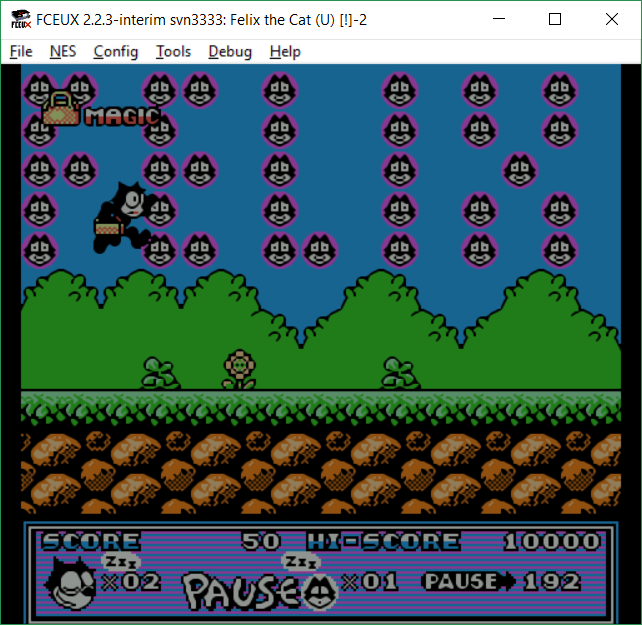
First of all, we check which blocks are used in the game. To do this, you can use the NesBlockFinder automatic block search utility . All that needs to be done is to feed her a dump of video memory of a loaded level (there will be no detailed instructions on how to do this, I will not stop in more detail to get to the main topic - compression analysis). NesBlockFinder produces the following results:

As you can see, the program detected 2x2 blocks in the ROM file, described by separate 4 arrays of 128 bytes each , and assumed the start address of the first array 0x17D2D .
Now you can change the bytes that make up one of the entire blocks in the emulator to make sure that the blocks on the screen change:

It is clearly seen that the green block inside the bushes has changed.
The next step is to designate the beginning and end of the block description arrays. To do this, you can simply change the bytes in front of the detected block, and also take into account the fact that in most games the first block consists of zeros only (there is no special reason for this, but this is found in almost all games). So the address of the beginning of the block description arrays is detected - 0x17D2A (and, accordingly, the addresses 0x17DAA, 0x17E2A, 0x17EAA for arrays of the following quarters of blocks). The end of the array is also easy to compute - the size of each part is known (128 bytes), so the end of the last array will be located at 0x17F2A .
The graphics on NES are designed so that in addition to describing the number of tile blocks, developers need to store block attributes (palette color indices), so you should always carefully study the data in front of the block array and immediately after it - most often the block attributes will be described there. This is also true for our Felix The Cat , behind the block description array there is an array of 128 bytes, in which for each block its palette attributes (in the upper two bits) and physical properties (in the lower six bits) are indicated. This is demonstrated in the screenshot:

The attribute area is highlighted on it and the high-order bits are changed in order to change the color of the test block.
Using the received addresses, you can take a dump of the video memory bank and palette (in detail, how to do this in the article, section “Step 6. Finding the address of the video memory bank and the level palette”) to build all the blocks used on the level.
To draw all the blocks, I used the Python language and Jupyter laptops, as well as C # modules for building NES graphics from the CadEditor editor (for gluing Python and C # I took the clr module , which allows loading .NET assemblies from Python and calling code from them).
The basic code for building blocks looks simple:
We get this result:

→ Commented laptop
Now that we have the blocks, we need to find out how the level is assembled from them. To do this, use the NesAutoСorrupter script . On working with the old version of the script, I wrote an entire article on the hub , since then I have significantly improved it (now it works ten times faster and requires only two game saves, without the need for manual calculations), but detailed documentation on the new version has not yet prepared, so I will limit myself to a brief description of working with him.
You must run the autocorrupter4.lua script in the FCEUX emulator, prepare 2 save files (immediately before loading the level and immediately after loading) and just press the “E” key to start work. The script receives all the necessary data from these files and changes each byte that was used between the two saves one by one, and then checks if the image on the screen has changed. The script saves the changed versions to files whose name contains the address of the changed byte.
Consider the result of the script for Felix The Cat . Pictures of changing bytes with addresses 0x1B940, 0x1B942, 0x1B944 , etc., in steps of 2, I put together for clarity in a gif picture:
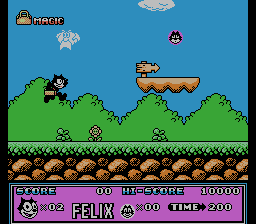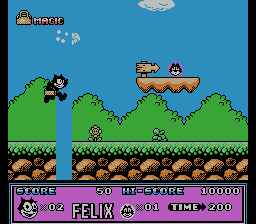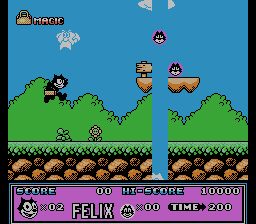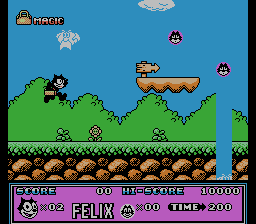
It follows from it that the level is described by vertical lines, and a step of 2 bytes indicates that these addresses are not just indexes, but addresses (pointers) on the line.
The address 0x1A904 is also of interest , the change of which leads to the change of exactly one block in the second line, therefore, this is the description area of the array of the lines themselves:

Now, poking at bytes in the vicinity of these addresses and analyzing the result, we come to such interesting conclusions about the level structure:
For example, consider the decompression of the first line.
Description of the compressed line:

Thus, we can already write the decompression of all lines:
And display them in the CadEditor level editor :

We got the opportunity to unzip the level and edit it, but to insert it back into the game you also need a reverse algorithm that will compress the data, and it will do it no worse than the compressor from the developers, otherwise they will not fit in the designated place. You can, of course, modify the pointers to the data so that they are placed in a separate bank and do not use compression at all, but this is not always possible, and the competition for the quality of compression with the game developers is too interesting a task to pass by - if for decryption of the decompressor, you can use a ready-made dictionary obtained in an unknown way, then for the compressor you need to learn how to compose a compression dictionary yourself.
The first idea of compiling a dictionary that came to my mind is simplywrite a list of all found RLE chains and sort it by replacement value . The replacement value is quite simple to calculate: it is necessary to calculate how many bytes will be saved on one replacement (chain length minus 1 byte) and multiply by the number of possible replacements.
Such an algorithm gave a result of 3879 bytes versus 3740 bytes in the original (loss by ~ 2%). It seemed to me not enough, and I began to reflect on how the developers did better.
After each replacement of the most profitable chain, the second idea was to immediately insert a word from the dictionary in its place . The result is 4695a byte, much worse than what it was. I realized that it is impossible to replace the chain until the dictionary is completely filled - perhaps in the future there will be a replacement that is more advantageous in the specific case (but less valuable from the point of view of the entire archive).
Thus, it is necessary to cross both algorithms - keep the complete dictionary in memory, but with a real replacement, update the value of all other replacements and sort it again by the updated value (if we replace, for example, a chain of 16 zeros with a word in the dictionary, then all shorter chains of zeros will now be found 1 times smaller).
However, such an implementation seemed to me too complicated and instead I just made the algorithm iterative - at each step a complete possible dictionary is compiled, and then the data is compressed by it with notes, which word is real how many timeswas used. After that, the dictionary is sorted by real rather than estimated value, and a forbidden dictionary is composed of words that have never been used (or their use has brought the least value). Then the cycle repeats, but so that the words from the forbidden dictionary no longer fall into the potential dictionary. The improvement operation can be repeated until the forbidden dictionary is no longer replenished. Then it remains only to take the maximum allowable number of values (128 words) from the real dictionary - this will be the best dictionary for compression. Thus, finally, it turned out to “catch up” with the developers, and get the same 3740compressed data, like them. With the other levels, the situation repeated - the results of the pinched data completely coincided with the original ones, although my dictionary was somewhat different.
The final function of building the dictionary (somewhat confusing because I experimented with different parameters and the dynamic value of the replacement). A dictionary of "forbidden" values is passed to the forbiddenArr parameter .
It's a little disappointing that after various experiments and improvements to the algorithm, I came across the optimal method that the developers used, but at least my compressor worked no worse than theirs. For all levels except the second, the results of clamping were the same, but with the second an interesting point was discovered - the decompressor broke on it. It turned out that the authors of the game for the level inside the pyramid (2-2 and 2-3) used an additional type of compression to compress the mosaic on the walls of the pyramids, which consists in using “ baselines ”.
The last 4 values of the blocks 0xFC-0xFF are used to encode specific commands.
In this case, a two-byte command (baseline_number, number of blocks from the baseline ). At the level, 4 baselines are used (their numbers are encoded from 0xFC to 0xFF ). The first few blocks are taken from this line, and then the lower part is drawn in the usual way.
An example of such line beginnings in the screenshot:

Repeating baselines are marked with frames on it. This compression method works at other levels, however, the baselines (common tops of the lines) are not described for them, so the developers did not use it, but it would save a few more bytes that are not practical, but symbolic in a mental competition with game developers .
Final Commented Notebookwith decompression and compression tests for all levels, which can be used to directly compress data and insert it into a ROM file.
Thus, the use of compression using the RLE dictionary, as well as the preservation of indexes of repeating lines, allow you to compress level descriptions in size of 18 kilobytes (256 x 3 x 24 blocks) to 4-5 kilobytes.

Block search
First of all, we check which blocks are used in the game. To do this, you can use the NesBlockFinder automatic block search utility . All that needs to be done is to feed her a dump of video memory of a loaded level (there will be no detailed instructions on how to do this, I will not stop in more detail to get to the main topic - compression analysis). NesBlockFinder produces the following results:

As you can see, the program detected 2x2 blocks in the ROM file, described by separate 4 arrays of 128 bytes each , and assumed the start address of the first array 0x17D2D .
Now you can change the bytes that make up one of the entire blocks in the emulator to make sure that the blocks on the screen change:

It is clearly seen that the green block inside the bushes has changed.
The next step is to designate the beginning and end of the block description arrays. To do this, you can simply change the bytes in front of the detected block, and also take into account the fact that in most games the first block consists of zeros only (there is no special reason for this, but this is found in almost all games). So the address of the beginning of the block description arrays is detected - 0x17D2A (and, accordingly, the addresses 0x17DAA, 0x17E2A, 0x17EAA for arrays of the following quarters of blocks). The end of the array is also easy to compute - the size of each part is known (128 bytes), so the end of the last array will be located at 0x17F2A .
The graphics on NES are designed so that in addition to describing the number of tile blocks, developers need to store block attributes (palette color indices), so you should always carefully study the data in front of the block array and immediately after it - most often the block attributes will be described there. This is also true for our Felix The Cat , behind the block description array there is an array of 128 bytes, in which for each block its palette attributes (in the upper two bits) and physical properties (in the lower six bits) are indicated. This is demonstrated in the screenshot:

The attribute area is highlighted on it and the high-order bits are changed in order to change the color of the test block.
Using the received addresses, you can take a dump of the video memory bank and palette (in detail, how to do this in the article, section “Step 6. Finding the address of the video memory bank and the level palette”) to build all the blocks used on the level.
Render blocks
To draw all the blocks, I used the Python language and Jupyter laptops, as well as C # modules for building NES graphics from the CadEditor editor (for gluing Python and C # I took the clr module , which allows loading .NET assemblies from Python and calling code from them).
The basic code for building blocks looks simple:
# CadEditor function for loading the config of blocks from the file
Globals.loadData (romName, dumpName, configName)
# We create an instance of the plug-in for rendering NES graphics
video = Video ()
#clr does not understand overloaded functions, therefore we explicitly set the prototype of the function we want to call
# Bitmap [] makeObjects (byte videoPageId, byte tilesId, byte palId, float scale, MapViewType drawType, int constantSubpal = -1);
makeObjects = video.makeObjects.Overloads [System.Byte, System.Byte, System.Byte, System.Single, MapViewType, System.Int32]
bb = makeObjects (0x90, 0, 0, 2.0, MapViewType.Tiles, -1)
# A bit of magic for converting Python arrays to C # array
blocks = System.Array [System.Drawing.Image] (bb)
fn = picPath + "blocks0.png"
# Gluing blocks into a rectangular image
UtilsGDI.GlueImages (blocks, 16, 8) .Save (fn)
# IPython function to display a saved picture in a laptop
display (Image (filename = fn))
We get this result:

→ Commented laptop
Level Description Format
Now that we have the blocks, we need to find out how the level is assembled from them. To do this, use the NesAutoСorrupter script . On working with the old version of the script, I wrote an entire article on the hub , since then I have significantly improved it (now it works ten times faster and requires only two game saves, without the need for manual calculations), but detailed documentation on the new version has not yet prepared, so I will limit myself to a brief description of working with him.
You must run the autocorrupter4.lua script in the FCEUX emulator, prepare 2 save files (immediately before loading the level and immediately after loading) and just press the “E” key to start work. The script receives all the necessary data from these files and changes each byte that was used between the two saves one by one, and then checks if the image on the screen has changed. The script saves the changed versions to files whose name contains the address of the changed byte.
Consider the result of the script for Felix The Cat . Pictures of changing bytes with addresses 0x1B940, 0x1B942, 0x1B944 , etc., in steps of 2, I put together for clarity in a gif picture:

It follows from it that the level is described by vertical lines, and a step of 2 bytes indicates that these addresses are not just indexes, but addresses (pointers) on the line.
The address 0x1A904 is also of interest , the change of which leads to the change of exactly one block in the second line, therefore, this is the description area of the array of the lines themselves:

Now, poking at bytes in the vicinity of these addresses and analyzing the result, we come to such interesting conclusions about the level structure:
- At 0x1B940 there is a large array of pointers on the line from which all three starting levels are built (1-1, 1-2, 1-3). Using pointers rather than indexes allows you to describe more than 256 lines (namely 256x3 = 768 lines ). To switch from a Pointer (a pointer in the address space of the CPU NES) to an absolute address in ROM, you need to add to the Pointer the address of the beginning of the bank in which it lies ( 0x10010 for the first level, other banks use other banks).
- Pointer to the first column = 0xA8ED , in translation to the absolute address - 0x1A8FD , from this address and further on there is a description of the lines, the height of each line is 24 bytes (this is a constant for all levels of the game).
- We examine the description of one of the lines and notice that if the block number in it is from 0x00 to 0x80 , then the block with the corresponding number is inserted directly into the final line; if the number is greater than 0x80, then a whole strip of different numbers of any blocks is inserted. An interesting conclusion follows from this - the game uses RLE compression to describe chains of identical blocks in a row, and these chains are collected in a dictionary, and encoded by indices in this dictionary!
- RLE dictionary address for the first level: 0x1B799 . Bytes are written to this address (the number of repeating blocks, the number of the repeat block ).
For example, consider the decompression of the first line.
Description of the compressed line:
[81 30 82 07 4C 83]And the dictionary:
[(24, 0x0) (17, 0x0) (2, 0x3) (2, 0x78)]First byte 81 - encodes the first value from the dictionary "take block 0 times 17 ", then block 30 follows , then byte 82 , which means taking the second value from the dictionary - "take block 3 2 times ", then blocks 07 and 4C follow , and finally, the value of 83 - the third word in the dictionary, "to take a 2 -fold unit 78 ". The output is the line:
[00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 30 03 03 07 4C 78 78]Here is a visual explanation of this unclenched line:

Thus, we can already write the decompression of all lines:
def decompressLine (d, addr, LINE_HEIGHT = 24):
ans = []
while len (ans) <LINE_HEIGHT:
v = d [addr]
# regular tile
if v <0x80:
ans.append (v)
# value from the RLE dictionary
else:
cv = v & 0x7F
repeatCount, repeatTile = compressedArr [cv]
ans.extend ([repeatTile] * repeatCount)
addr + = 1
return ans
And display them in the CadEditor level editor :

Compressor
We got the opportunity to unzip the level and edit it, but to insert it back into the game you also need a reverse algorithm that will compress the data, and it will do it no worse than the compressor from the developers, otherwise they will not fit in the designated place. You can, of course, modify the pointers to the data so that they are placed in a separate bank and do not use compression at all, but this is not always possible, and the competition for the quality of compression with the game developers is too interesting a task to pass by - if for decryption of the decompressor, you can use a ready-made dictionary obtained in an unknown way, then for the compressor you need to learn how to compose a compression dictionary yourself.
The first idea of compiling a dictionary that came to my mind is simplywrite a list of all found RLE chains and sort it by replacement value . The replacement value is quite simple to calculate: it is necessary to calculate how many bytes will be saved on one replacement (chain length minus 1 byte) and multiply by the number of possible replacements.
Such an algorithm gave a result of 3879 bytes versus 3740 bytes in the original (loss by ~ 2%). It seemed to me not enough, and I began to reflect on how the developers did better.
After each replacement of the most profitable chain, the second idea was to immediately insert a word from the dictionary in its place . The result is 4695a byte, much worse than what it was. I realized that it is impossible to replace the chain until the dictionary is completely filled - perhaps in the future there will be a replacement that is more advantageous in the specific case (but less valuable from the point of view of the entire archive).
Thus, it is necessary to cross both algorithms - keep the complete dictionary in memory, but with a real replacement, update the value of all other replacements and sort it again by the updated value (if we replace, for example, a chain of 16 zeros with a word in the dictionary, then all shorter chains of zeros will now be found 1 times smaller).
However, such an implementation seemed to me too complicated and instead I just made the algorithm iterative - at each step a complete possible dictionary is compiled, and then the data is compressed by it with notes, which word is real how many timeswas used. After that, the dictionary is sorted by real rather than estimated value, and a forbidden dictionary is composed of words that have never been used (or their use has brought the least value). Then the cycle repeats, but so that the words from the forbidden dictionary no longer fall into the potential dictionary. The improvement operation can be repeated until the forbidden dictionary is no longer replenished. Then it remains only to take the maximum allowable number of values (128 words) from the real dictionary - this will be the best dictionary for compression. Thus, finally, it turned out to “catch up” with the developers, and get the same 3740compressed data, like them. With the other levels, the situation repeated - the results of the pinched data completely coincided with the original ones, although my dictionary was somewhat different.
The final function of building the dictionary (somewhat confusing because I experimented with different parameters and the dynamic value of the replacement). A dictionary of "forbidden" values is passed to the forbiddenArr parameter .
def rebuildCompress (screen, forbiddenArr, maxCompressSize = 256, LINE_LEN = 24):
fullAns = [(0,0)] * maxCompressSize
lines = list (chunks (screen, LINE_LEN))
x = 0
while x <maxCompressSize:
ans = {}
for line in lines:
repeats = [list (g) for _, g in groupby (line)]
repeats = [(g [0], len (g)) for g in repeats]
for (tileNo, tileCount) in repeats:
#for tc in xrange (tileCount, tileCount + 1):
for tc in xrange (2, tileCount + 1):
compressPair = tileNo, tc
if compressPair in ans:
ans [compressPair] + = 1
else:
ans [compressPair] = 1
# calculation of replacement value - chain length * frequency of occurrence
def calcPoints (v):
(t, c), cnt = v
return - (c-1) * cnt
ans = sorted (ans.iteritems (), key = calcPoints)
#filter and reverse values
newAns = []
for a in ans:
if (a [0] [0]) <0x80:
newAns.append ((a [0] [1], a [0 ] [0]))
newAns = filter (lambda v: v not in forbiddenArr, newAns)
if len (newAns) == 0:
break
#HINT !!! if first results are similar in points, then we can use it's all
ansValue = newAns [0] [1]
#newAns = filter (lambda x: x [1] == ansValue, newAns) #comment this for best results!
#newAns = sorted (newAns, key = lambda x: -x [0])
#print newAns
similar, maxSimilar = 0, 256
while len (newAns)> 0 and x <maxCompressSize and similar <maxSimilar:
curAns = newAns [0]
lines, findAtLeastOneReplace = compressorReplace (lines, curAns, x)
fullAns [x] = curAns
x + = 1
similar + = 1
newAns = newAns [1:]
return fullAns
Second type of compression
It's a little disappointing that after various experiments and improvements to the algorithm, I came across the optimal method that the developers used, but at least my compressor worked no worse than theirs. For all levels except the second, the results of clamping were the same, but with the second an interesting point was discovered - the decompressor broke on it. It turned out that the authors of the game for the level inside the pyramid (2-2 and 2-3) used an additional type of compression to compress the mosaic on the walls of the pyramids, which consists in using “ baselines ”.
The last 4 values of the blocks 0xFC-0xFF are used to encode specific commands.
In this case, a two-byte command (baseline_number, number of blocks from the baseline ). At the level, 4 baselines are used (their numbers are encoded from 0xFC to 0xFF ). The first few blocks are taken from this line, and then the lower part is drawn in the usual way.
An example of such line beginnings in the screenshot:

Repeating baselines are marked with frames on it. This compression method works at other levels, however, the baselines (common tops of the lines) are not described for them, so the developers did not use it, but it would save a few more bytes that are not practical, but symbolic in a mental competition with game developers .
Final Commented Notebookwith decompression and compression tests for all levels, which can be used to directly compress data and insert it into a ROM file.
Thus, the use of compression using the RLE dictionary, as well as the preservation of indexes of repeating lines, allow you to compress level descriptions in size of 18 kilobytes (256 x 3 x 24 blocks) to 4-5 kilobytes.
