Roadmap of mathematical disciplines for machine learning, part 1
- Tutorial
Instead of the preface
Suppose, sitting in the evening in a warm armchair, you suddenly had a crazy thought: “Hmm, why don't I find out instead of random selection of hyperparameters of the model, and why does it all work?”
This is a slippery slope - you think that a couple of evenings with a leisurely reading of the “Deep Learning” chapter or 5-minute youtube videos from various MOOCs are enough; in fact, to create an understanding, rather than an illusion, it takes a decent amount of time (well, no less than six months for the most fanatical); but the saddest thing is that the profit from this event is not obvious - fortunately (or unfortunately), the world is not arranged according to the laws of mathematics, and whether you are a doctor of physics and physics three times - some models will still work better only if you throw They have more preprocessed data or build a huge ensemble.
I consider it my duty to warn you that this is a curved path, and it is possible that investments in mathematics will not pay off as soon as desired. But mathematics is interesting in itself, regardless of applications. Moreover, if you are interested in, and what happens in this black box with hyper parameters, then this means that you probably are not indifferent to mathematics.
One more thing about my recommendations: I do not like math literature, which is teeming with indices, pearls like “a_ijk with three underscores and a cap conjugate”. I think ideas are more important than rigorous conclusions. At the same time, ideas should not slide down to “handshaking”; everything should be rather strict. I do not like books like Bourbaki and Knut. In my opinion, these books are intended for anything, but not for reading or for studying the subject. They are good as references and as encyclopedias.
Finally, here are some of Bertrand Russell:
Euclid despised the practical utility that Plato introduced. It is said that one student, after hearing the evidence, asked what he would gain by studying geometry; then Euclid called a slave and said: "Give the young man a penny, because he must certainly benefit from what he studies."I now turn to the main part.
Prerequisites
- I assume that you are more or less oriented to school mathematics.
- I assume that you don’t speak English very well with “you,” since a lot of practical literature and courses are written and told in this language. Mathematical English is not as scary as English in general; it is a rather limited vocabulary with standardly constructed sentences, without a jumble of times, without a riot of colors, etc.
- I assume that you have a rope with which you can tie yourself to a chair.
Difficulty levels
It is no secret that a lot of literature has been written in every mathematical discipline, and sometimes even a simple choice of the right book becomes a problem. I will highlight several levels of complexity in the literature, that you knew where to go and where to go (for now) it is not necessary (or what can be addressed for more complete information).
- Bring it on - the main workhorse; these are books that are called “must have”.
- Hurt me plenty - a higher level, allows you to look at level 1 from a bird's eye view, organizes knowledge, combines various areas of knowledge.
- Nightmare - for the strong in spirit, the level of mekhmat, for lovers of mathematics and ivory towers.
Road map
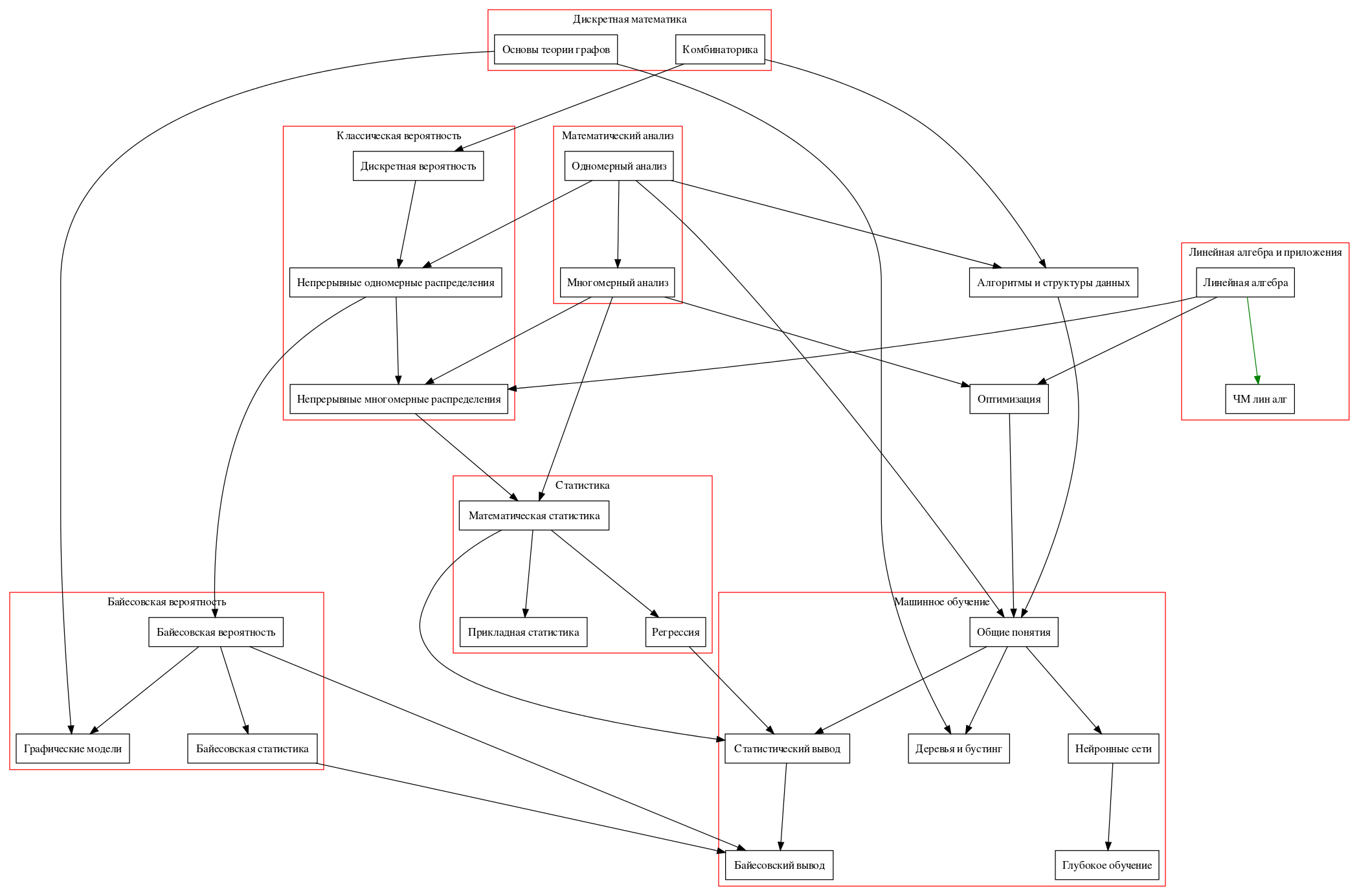
I will go on to specific courses.
Analysis, he's a calculus
In Russian universities, it is taught quite interestingly: most of them, a few years after the end of the course, only some integrals vaguely remember, and it seems something else. And this is despite the fact that analysis is a discipline directly one of the fundamental in mathematics in general. There are usually no bridges from theory to practice, and this course, like a flying island, hovers somewhere in the head, completely divorced from real life. It is necessary to overcome this by solving problems, and not only from the field of mathematics, but also preferably something from “real life”.
What you need to know from the analysis?
The main things we need are the concept of limit, continuity, derivative, functions of several variables, gradient, integral, integral with variable upper limit, multidimensional integral *.
Literature
Bring it on : everything is more or less standard - Piskunov / Fichtenholz .
Hurt me plenty : Zorich, volume 1 . I love this book very, very much; This is not a textbook, but a novel in formulas, something like Eugene Onegin. Unfortunately, it is more complicated than standard courses on analysis due to the fact that many things in it are given more generally, and you need to get used to it; but at the expense of this community many different things are tied together (see the same limits on the base).
Nightmare : Zorich tom1 + tom2, Rudin "Fundamentals of mathematical analysis", Lviv "Lectures on mathematical analysis", Ramanan "Global Calculus".
In general, the summary here is this: the literature on the analysis is even full in Russian; textbooks more often to purely mathematical. As a supplement to textbooks of level 2-3, I can advise several courses:
I did not look at the courses from the lecture hall of MIPT on analysis, but for the sake of completeness I will also give:
Practice
To practice and apply the gained knowledge is not that “optional”, but strictly MANDATORY, otherwise the whole theory will hang on you as a dead weight, and you will quickly go to the bottom, even without realizing it.
I propose to consider the following options: Demidovich, problem sets from MIT courses (https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/index.htm)
Linear algebra
Sustainable bread for Data Science and in general for science in general. Unfortunately, people have learned to solve only linear equations and their systems well; for equations of degree 2 and above, there are all very nontrivial theories (commutative algebra, algebraic geometry, and others like them). Therefore, in data analysis, linear models are mainly used (or generalized linear models, such as logistic regressions, perceptrons, etc.).
There are many books on linear algebra in Russian. The problem is that they are written either for mathematicians, or there are depressingly many indexes in them (and there is no forest behind the trees). Often the emphasis in university courses is on Jordan form; other standard forms are often not mentioned; there is Gauss and stupid Kramer, but rarely what happens about LU, about SVD.
What you need to know from linear algebra?
The concept of vector and vector space; the concept of a linear operator; communication of operators and matrices; matrix expansions (LU, SVD at least); eigenvectors and eigenvalues; orthogonal, unitary operators; symmetric and Hermitian operators; quadratic forms, leading to the main axes.
Literature
Bring it on : OCW-MIT course of Gilbert Strang on linear algebra + his book .
ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/index.htm
The most good thing about this course is the absence of "complex" and rather senseless theorems of linear algebra, of all dual spaces, a large number of problems in the book, a practice-oriented approach (not “what it is,” but “how to calculate it”). More sensible courses on linear algebra, I have not yet met.
Hurt me plenty : Axler "Linear algebra done right"; Gelfand "Lectures on linear algebra "; MIPT course lectoriy.mipt.ru/course/LinearAlgebra ; Kostrikin "Introduction to Algebra, Part 2", Tyrtyshnikov "Matrix Analysis and Linear Algebra".
The problem of books and courses from this level of complexity is that they are theoretical-oriented. There are linear functionals and dual spaces, but there is no projection matrix on the subspace and no practical ways to calculate the eigenvalues. Most likely, courses from this level will have to be supplemented by strong practice; for example, numerical methods of linear algebra.
About the last book separately. In my opinion, this is one of the most successful Russian-language books on linear algebra in the sense that it is not very divorced from practice; while it contains all sorts of "advanced" topics. To some extent, it can replace Strang’s lectures completely, but it should be supplemented with simple tasks to “tamper with the hand”. There are some problems in this book, but they are rather severe.
Nightmare :Kostrikin-Manin, Linear Algebra and Geometry, Shafarevich-Remizov, Linear Algebra and Geometry.
In general, there is a lot of good literature in Russian, especially at the last level, but it suffers from excessive complexity.
Practice
As in the first case, the practice is obligatory. Pass SVD - study image compression. Pass through matrix multiplications — study the fast Fourier transform, the Strassen algorithm; solve many problems (for example, from Kostrikin’s or Proskuryakov ’s problem book ); write your LU decomposition, Gauss. For the most stubborn, I can offer wonderful books on numerical methods of linear algebra, such as Trefethen, Bau "NUMERICAL LINEAR ALGEBRA"; Horn, Johnson Matrix Analysis . These books will be useful, firstly, for the "stuffing" of the hand; secondly, it will immediately become clear that many theoretical methods are broken into pieces about the prose of life (machine accuracy, method instability, work with sparse matrices).
Discrete Math
Another whale of modern CS. Here we will mainly be interested in combinatorics and fundamentals of graph theory.
What you need to know from combinatorics and graph theory?
Binomial coefficients, their asiptotics; graphs; trees; search depth and width; recursive relations and their solutions;
Literature
Bring it on : Anderson, J. Discrete Mathematics and Combinatorics; Haggarty, Schlipf J., Whitesides S. “Discrete Mathematics for Programmers”, Ore O. “Graphs and Their Applications” .
The first two books are excellent Talmuds in discrete mathematics, covering almost all the questions that need to be known.
Hurt me plenty : Graham, Knut, Patashnik "Concrete Mathematics", Harari "Graph Theory", Ore "Graph Theory".
Nightmare : Sachkov “Introduction to combinatorial methods of discrete mathematics”, Omelchenko “Graph theory”.
Practice
As a rule, a large number of tasks are included in combinatorics textbooks; they need to be resolved. In fact, all combinatorics is the art of solving various problems, rather than some kind of unified theory.
