Clustering text documents by semantic attributes (part two: description of models)
Word2Vec Models
As mentioned in the first part of the publication , models are obtained from classes - representing the result of the word2vec text as associative-semantic classes by smoothing out distributions.
The idea of smoothing is as follows.
- We get a frequency vocabulary of training material, where each word is assigned its frequency of occurrence according to documents (i.e., in how many documents is this token encountered).
- Based on this frequency distribution, for each word of the class its standard deviation is considered (or variance, in this case, does not have a fundamental difference).
- For each class, we consider the average of all deviations of its components.
- From each class we remove “outliers” - words with a large standard deviation:
Where SDw is the standard deviation of each word, avr (SDcl) is the class average root mean square, and k is the smoothing coefficient.
Obviously, the result will depend on the coefficient k. His choice is an empirical task, it depends on the language, the size of the training sample, its homogeneity, etc. But still we will try to identify some common things.
Building and testing models
For the models, material collected from the daily Internet stream, collected from the lists of the most frequency keywords, was used. The English text contained about 170 million word forms, Russian - a little less than a billion. The range of the number of classes was from 250 to 5000 classes in increments of 250. The remaining parameters were used by default.
Testing was conducted on Russian-language and English-language material.
The testing methodology in a nutshell is as follows: reference test cases were taken for classification and run through clustering models with various parameters: by changing the number of classes and the smoothing coefficient, you can demonstrate the dynamics of the result, and, consequently, the quality of the model.
The English five corps are taken from open source :
- 20NG-TEST-ALL-TERMS - 20 topics (10555K)
- MINI20-TEST - 20 topics (816K)
- R52-TEST-ALL-TERMS - 52 threads (1487K)
- R8-TEST-ALL-TERMS - 8 topics (1167K)
- WEBKB-TEST-STEMMED - 4 threads (1271K)
Russian cases had to be used from closed development, since it was not possible to find open sources:
- Ru1 - Short Message Corps - 13 topics (76K)
- Ru2 - News Building - 10 topics (577K)
During testing, the simplest comparison method was used, without the use of any complex metrics. The choice in favor of such a simple classification (Dumb classifier) was made in view of the fact that the purpose of the study was not to improve the classification result, but to compare the results with different input parameters. That is, it was not the result itself that was interesting, but its dynamics.
At the same time, tests were carried out on some clustering models using the TFiDF logarithmic measure to check how fundamentally these results on these models can differ from the results on models trained on lexical unigrams. Such tests showed that the results on models with associative-semantic classes are almost not inferior to models on unigrams: there was a slight deterioration in quality from 1 to 10%, depending on the test case. This indicates the competitiveness of the obtained clustering models, given that they were not initially “tailored” to the topics.
The dependence of the quality of the model on the number of classes
Tests with different numbers of semantic classes were conducted with all cases: from 250 to 5000 with a step of 250 classes.
Figures 1 and 2 show the dependence of the classification accuracy on the number of model classes for the Russian and English languages.

Fig. 1. Dependence of classification accuracy on the number of word2vec semantic classes for Russian-language corps. On the abscissa axis, the number of classes; on the ordinate axis, precision values.

Fig. 2. Dependence of classification accuracy on the number of word2vec semantic classes for English-language cases. The abscissa axis represents the number of classes, and the ordinate axis represents the classification accuracy.
The graphs show that fluctuations in accuracy are periodic in nature, the period of which may vary depending on the material being tested. To determine the trends, we construct graphs of average values.

Fig. 3. The average value is the dependence of the classification accuracy on the number of word2vec semantic classes for Russian-language cases. On the abscissa axis, the number of classes; on the ordinate axis, precision values. Added a polynomial (6th degree) trend line.

Fig. 4. The average value is the dependence of the classification accuracy on the number of word2vec semantic classes for English-language cases. On the abscissa axis, the number of classes; on the ordinate axis, precision values. Added a polynomial (6th degree) trend line.
From Figures 3 and 4 it is already evident that the quality of the result on average grows with an increase in the number of classes in the range from 4 to 5 thousand. Which, generally speaking, is not surprising: a more subtle partition of space leads to its concretization. But further splitting can lead to the fact that semantic classes begin to stratify into homogeneous pieces. And this already leads to a drop in accuracy, for classes cease to be “hooked”: different semantic classes will correspond to the same meaning. This is observed in the approximation of 5 thousand classes for both Russian and English.
The peaks present in both figures in the region of 500 classes are curious: despite the fact that there are few semantic classes (therefore, the classes are mixed), nevertheless, macro-semantic unification is observed: classes generally gravitate to one topic or another.
From the results obtained, it can be concluded that, nevertheless, a more optimal partition can be somewhere between 4 and 5 thousand classes.
The dependence of the quality of the model on the smoothing coefficient.
Figure 5 shows changes in the classification accuracy for the R8 case at different smoothing factors (for 1500 classes). The frequency of changes for any number of classes within the same building is the same. Similar graphs are observed for all cases.
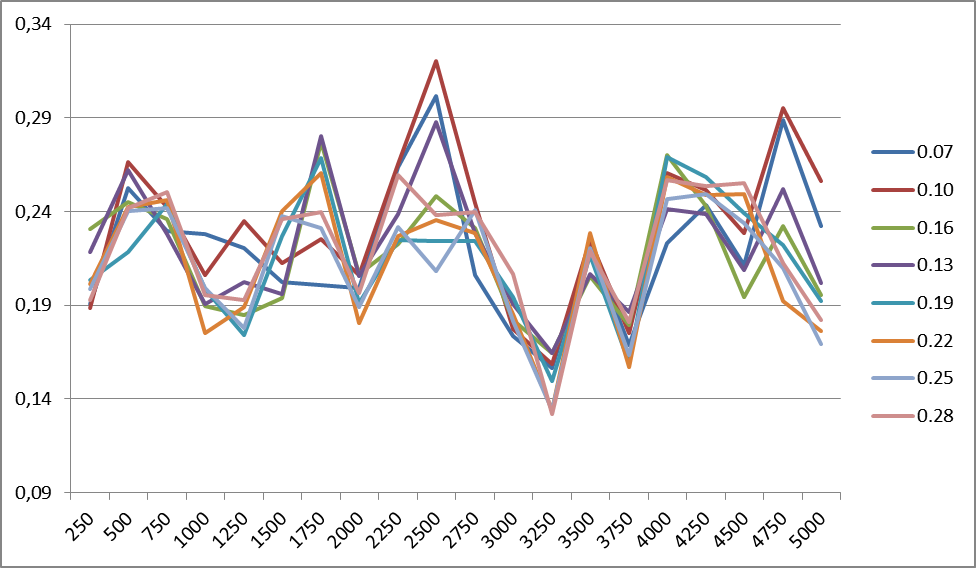
Fig. 5. Changes in classification accuracy for the R8 case for different values of the smoothing coefficient. On the right are the values of the smoothing coefficient.
To identify the main trends, we will construct graphs of the average values of the accuracy of the smoothing coefficient for all cases for English and Russian languages.
 | 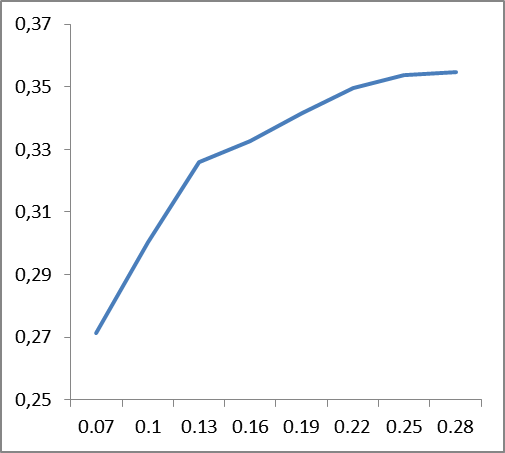 |
Figure 6. Dependence of changes in classification accuracy (vertical) on the values of smoothing coefficients (horizontal), averaged data for buildings: left - for English, right - for Russian.
From the graphs presented in Fig. 6 it follows that the smoothing coefficient is language-dependent: if for the English language stability occurs somewhere around 0.22, then for Russian it is about 0.12. Apparently, this should be somehow connected with the complexity of the language, its perplexity.
It is difficult to say what explains the peak of accuracy at the beginning (0.07) for the English language. Its presence is caused by the behavior of the R8 case, and, possibly, due to the lexical content of the case itself.
In fact, if we compare the data of the models themselves with different smoothing coefficients, then it can be seen that at the above thresholds, some of the high-frequency words (prepositions, conjunctions, articles) are filtered. Therefore, it makes no sense to enter stop lists: this vocabulary is either filtered, or form a separate associative-semantic class with a fairly low weight.
The dependence of the variability of the smoothing coefficient on the number of classes has very little effect on the change in accuracy. However, it was not possible to identify any tendency of such an effect for different materials.
conclusions
Of course, this is not the only, and perhaps not the best method of obtaining models, because it is empirical and depends on many factors. In addition, smoothing can be done in much trickier ways. Nevertheless, this method allows you to quickly and efficiently build models and get good clustering results on large volumes of information.
We give an example of the use of clustering on Russian-language material.
Example
Clustering social media message flow with Sberbank search query. The number of messages is 10 thousand. This is approximately 10 MB of text or 5-6 hours of message flow on the topic of Sberbank.
As a result, 285 clusters were obtained, from where the main events concerning Sberbank are immediately visible.
Here, for example, the first ten clusters (headers of the first messages):
- Sberbank clients complain about malfunctions in the online service - 327 messages of this kind
- Jews want to privatize Sberbank in the next 3 years - 77 posts
- Sberbank answers, such as: <name> hello, unfortunately, at the moment there really are interruptions in work ... - 74 messages
- In 2017, Sberbank will conduct a test of quantum information transfer hi-tech - 73 messages
- in the year of its 175th anniversary Sberbank gives free entry to art museums - 71 messages
- learn about the benefits of a youth Sberbank visa debit card and how to buy a sweatshirt for n ruble - 57 messages
- Ministry of Economic Development proposes to include Sberbank in privatization plan - 58 posts
- Sberbank reported a malfunction in its systems - 60 messages
- Vladimir Putin took part in the conference forward to the future role and place of Russia - 61 messages (Sberbank also took part);
- Gref denied information on the privatization of Sberbank - 64 reports
Most likely, the 1st and 8th clusters can be combined into macro clusters based on additional information, for example, the use of geo-tags, message sources, predicative relationships between objects, etc. But this is another task, which we will talk about next time. .
You can get acquainted with examples and demo implementation of the algorithm here .
