AI in the game Hase und Igel: minimax for three

After the real boom of board games of the late 00s, several boxes of games remained in the family. One of them is the game “Hare and the Hedgehog” in the original German version. A multi-player game in which the element of chance is minimized, and sober calculation and the player’s ability to “look in” several steps ahead conquer.
My frequent defeats in the game led me to the idea of writing a computer “intellect” to select the best move. Intellect, ideally, able to compete with the grandmaster Hare and Hedgehog (and that tea, not chess, the game will be simpler). Further in the article there is a description of the development process, AI logic and a link to the sources.
Game rules Hare and Yozh
On the playing field in 65 cells, there are several player chips, from 2 to 6 participants (my drawing, non-canonical, looks, of course, so-so):
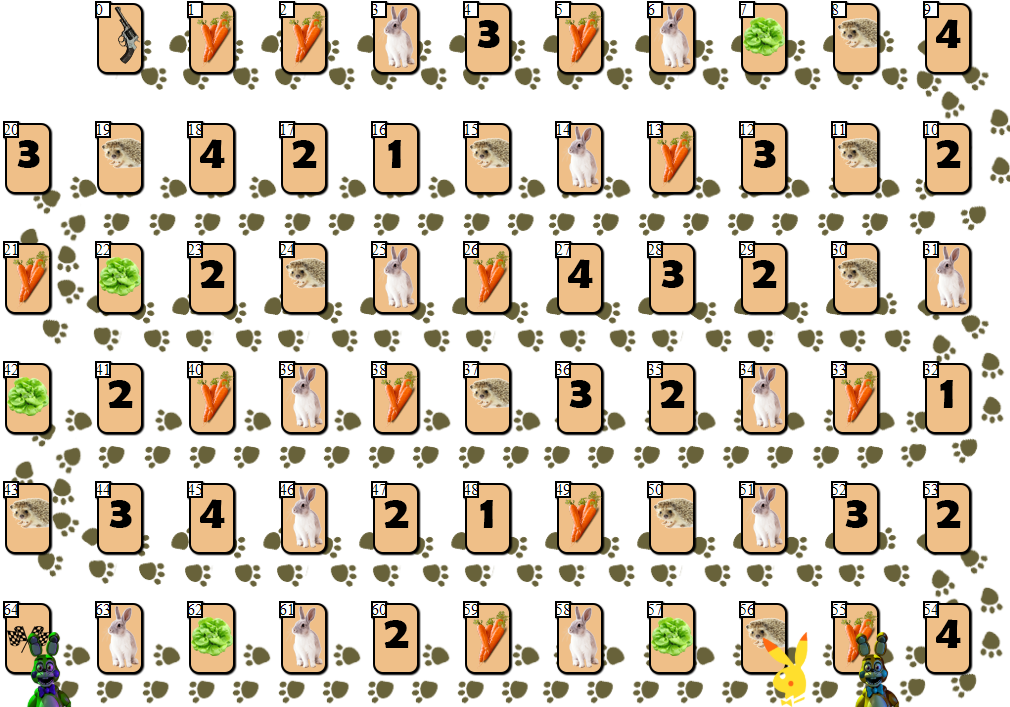
Apart from the cells with indices 0 (start) and 64 (finish), each cell can accommodate only one player. The goal of each player is to move forward to the finish cell, ahead of rivals.
The “fuel” for moving forward is a carrot - a game “ currency ”. At the start, each player receives 68 carrots, which he gives (and sometimes receives) as he moves.
In addition to carrots, the player receives 3 cards of lettuce at the start. Salad is a special “artifact” that a player must get rid of before the finish. Getting rid of the salad (and this can only be done on a special cage of lettuce, like this:

), the player, in particular, receives additional carrots. Before that, skipping your turn. The more players ahead of the salad leaving the card, the more carrots that player will receive: 10 x (position of the player on the field relative to other players). That is, the second player on the field will receive 20 carrots, leaving the lettuce cage.
Cells with numbers 1-4 can bring several dozen carrots if the player’s position coincides with the number on the cage (1-4, cage number 1 is also suitable for the 4th and 6th positions on the field), by analogy with the lettuce cage.
The player can skip the move, remaining on the cage with the image of carrots and get or give for this action 10 carrots. Why should a player give “fuel”? The fact is that a player can only finish having 10 carrots after his final move (20 if you finish second, 30 if you finish third, etc.).
Finally, the player can get 10 x N carrots by making N steps on the nearest free hedgehog (if the nearest hedgehog is busy, such a move is impossible).
The cost of moving forward is calculated not proportionally to the number of moves, according to the formula (rounded up):
Where N - number of steps forward.
So for a step forward one cell, the player gives 1 carrot, 3 carrots for 2 cells, 6 carrots for 3 cells, 10 for 4, ..., 210 carrots for moving 20 cells forward.
The last cage - the hare cage - introduces an element of randomness into the game. When a player gets into a cage with a hare, he pulls a special card from the pile, after which some action is taken. Depending on the card and the game situation, the player may lose some carrots, get extra carrots, or skip one turn. It should be noted that among the cards with “effects” there are several more negative scenarios for the player, which encourages the game to be cautious and calculated.
No AI implementation
In the very first implementation, which will then become the basis for the development of a game “intellect,” I have limited myself to the option in which every move is made by a player — a person.
I decided to implement the game as a client - a static one-page website, all of the “logic” of which is implemented on JS and the server is a WEB API application. The server is written in .NET Core 2.1 and produces at the output one artifact of the assembly - a dll file that can run under Windows / Linux / Mac OS.
The “logic” of the client part is minimized (just like the UX, since the GUI is purely utilitarian). For example, the web client does not perform the check itself - is the rules requested by the player allowed by the rules? This check is performed on the server. The server tells the client what moves the player can make from the current playing position.
The server is a classicMoore's machine gun . In the server logic, there are no such concepts as “connected client”, “game session”, etc.
All that the server does is process the received (HTTP POST) command. The “command” pattern is implemented on the server . The client can request the execution of one of the following commands:
- start a new game, i.e. “Arrange” chips of a specified number of players on a “clean” board
- make the move specified in the team
For the second team, the client sends the current game position to the server (an object of the Disposition class), that is, a description of the following form:
- position, the number of carrots and lettuce for each hare, plus an additional boolean field indicating that the hare is missing its turn
- index hare making a move.
The server does not need to send additional information - for example, information about the playing field. Just as for writing a chess etude it is not necessary to paint the arrangement of black and white cells on the board - this information is taken as a constant.
In the response, the server indicates whether the command was successful. Technically, a client may, for example, request an invalid move. Or try to create a new game for a single player, which obviously does not make sense.
If the team is successful, the response will contain a new playing position , as well as a list of moves that the next player in the queue (current for the new position) can make.
In addition to this, the server response contains some service fields. For example, the text of a hare card “pulled out” by a player during a step on the corresponding cell.
Player's move
The player's turn is encoded by an integer:
- 0 if the player is forced to remain in the current cell,
1, 2, ... N for 1, ... N steps forward, - -1, -2, ... -M to move 1 ... M cells back to the nearest free hedgehog,
- 1001, 1002 - special codes for the player who decides to stay on the carrot cage and get (1001) or give (1002) 10 carrots for it.
Software implementation
The server receives the JSON of the requested command, parses it into one of the corresponding request classes, and performs the requested action.
If the client (player) requested to make a move with the CMD code from the position passed to the team (POS), the server performs the following actions:
- checks if such a move is possible
- creates a new position from the current one, applying corresponding modifications to it,
gets a lot of possible moves for the new position. Let me remind you that the index of the player making the move is already included in the object describing the position , - returns to the client a response with a new position, possible moves or the success flag equal to false, and a description of the error.
The logic of checking the admissibility of the requested move (CMD) and building a new position turned out to be connected a little more closely than we would like. The search method for permissible moves echoes this logic. All this functionality implements the class TurnChecker.
At the input of the validation / execution method of a turn, TurnChecker obtains an object of a game position class (Disposition). The Disposition object contains an array of player data (Haze [] hazes), the index of the player making the move + some service information that is filled in during the operation of the TurnChecker object.
The game field describes the FieldMap class, which is implemented as a singleton . The class contains an array of cells + some service information used to simplify / speed up subsequent calculations.
Performance considerations
In the implementation of the TurnChecker class, I tried, as far as possible, to avoid cycles. The fact is that the methods for obtaining the set of permissible moves / execution of the course will subsequently be called thousands (tens of thousands) of times during the search procedure for a quasi-optimal move.
So, for example, I calculate how many cells a player can go forward, having N carrots, according to the formula:
Checking if cell i is not occupied by one of the players, I do not run through the list of players (since this action will probably have to be performed many times), but I turn to a dictionary like [cell_ index, busy_cell flag] filled in advance.
When checking whether the specified hedgehog cell is the closest (behind) with respect to the current cell occupied by the player, I also compare the requested position with the value from the dictionary of the form [cell_ index, close_ index_below] with static information.
So, for example, I calculate how many cells a player can go forward, having N carrots, according to the formula:
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2;
Checking if cell i is not occupied by one of the players, I do not run through the list of players (since this action will probably have to be performed many times), but I turn to a dictionary like [cell_ index, busy_cell flag] filled in advance.
When checking whether the specified hedgehog cell is the closest (behind) with respect to the current cell occupied by the player, I also compare the requested position with the value from the dictionary of the form [cell_ index, close_ index_below] with static information.
Implementation with AI
One command is added to the list of commands processed by the server: execute a quasi-optimal, selected by the program, move. This command is a small modification of the “player's move” command, from which the move field ( CMD ) itself is removed .
The first solution that comes to mind is to use heuristics to select the “best possible” move. By analogy with chess, we can evaluate each of the game positions obtained with our move, putting some assessment of this position.
Heuristic position evaluation
For example, in chess, it is quite simple to make an assessment (without getting into the wilds of debuts): at a minimum, you can calculate the total “cost” of pieces, taking a knight / bishop cost for 3 pawns, a rook cost 5 pawns, a queen - 9, a king - int .MaxValue pawns. Estimation is easy to improve, for example, by adding to it (with a correction factor — a multiplier / exponent or a function):
- the number of possible moves from the current position,
- the ratio of threats to enemy figures / threats from the enemy.
A special assessment is given to the position of the mat: int.MaxValue , if the mat has set the computer, int.MinValue if the mat has been set by the person.
If you order the chess processor to choose the next move, guided only by such an assessment, the processor will probably choose not the worst moves. In particular:
- do not miss the opportunity to take a bigger figure or checkmate,
- most likely not pounding the figures in the corners,
- it will not expose the figure once again (considering the number of threats in the assessment).
Of course, such moves of the computer will not leave him a chance of success with the opponent making his moves more or less meaningfully. The computer will ignore any of the forks. In addition, it does not hesitate to even probably exchange a queen for a pawn.
Nevertheless, the heuristic evaluation algorithm of the current game position in chess (without claiming the laurels of the champion program) is quite transparent. That can not be said about the game Hare and Hedgehog.
In general, in the game Hare and Hedgehog, a rather blurry maxim works: “ it’s better to go far away with more carrots and less lettuce". However, not everything is so straightforward. For example, if a player has 1 salad card in his hand in the middle of a game, this option can be quite good. But the player standing at the finish with a salad card, obviously, will be in a losing situation. In addition to the evaluation algorithm, I would also like to be able to “peep” a step further, just as in a heuristic evaluation of a chess position, you can count threats to the pieces. For example, it is worth considering the bonus of carrots received by a player leaving a salad / cell position (1 ... 4), taking into account the number of players ahead.
I brought the final grade as a function:
E = Ks * S + Kc * C + Kp * P,
where S, C, P are scores calculated using lettuce cards (S) and carrots © on the hands of the player, P is the score, given to the player for the distance traveled.
Ks, Kc, Kp - the corresponding correction factors (they will be discussed later).
The easiest way I determined the estimate for the distance traveled :
P = i * 3, where i is the index of the cell where the player is located.
Grade C (carrots) is made more difficult.
To get a specific C value, I choose one of 3 functions
- [0], if the player has passed less than half of the playing field,
- [2] if the player has enough (m. B., Even with an excess) carrots to finish,
- [1] in other cases.
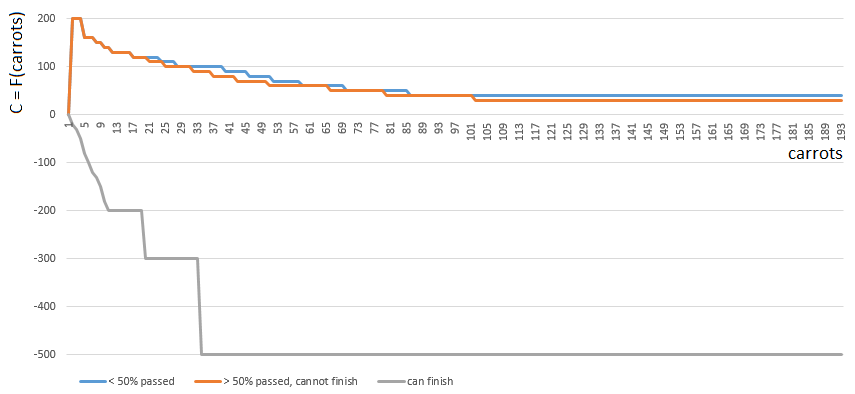
Functions 0 and 1 are similar: the “value” of each carrot in the hands of the player gradually decreases with increasing number of carrots in the hands. The game rarely encourages "Plyushkin." In case 1 (half of the field is passed), the value of the carrot decreases a little faster.
Function 2 (the player can finish), on the contrary, imposes a large penalty (a negative coefficient value) on each carrot in the player's hands - the more carrots, the greater the penalty factor. Since with an excess of carrot finish is prohibited by the rules of the game.
Before calculating the number of carrots in the player's hands is adjusted taking into account the carrots for the course from the cage of lettuce / cage with number 1 ... 4. The
“ salad ” grade S is displayed in a similar way. Depending on the amount of salad on the player’s hands (0 ... 3), the function is selected.
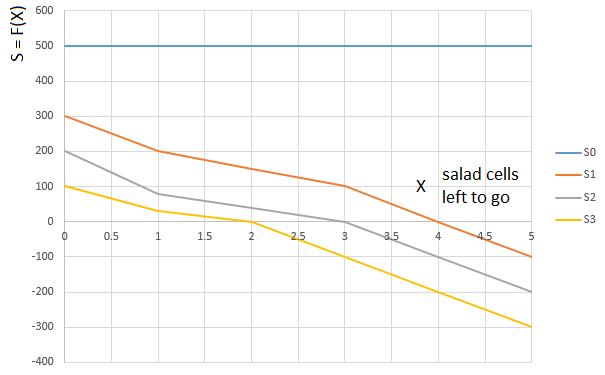
Curve
curve
The final score (E = Ks * S + Kc * C + Kp * P), therefore, takes into account:
- the additional amount of carrots that a player will receive immediately before his own turn,
- the path traveled by the player
- the number of carrots and lettuce on the hands, non-linearly affecting the assessment.
And this is how a computer plays, choosing the next move according to the maximum heuristic evaluation:
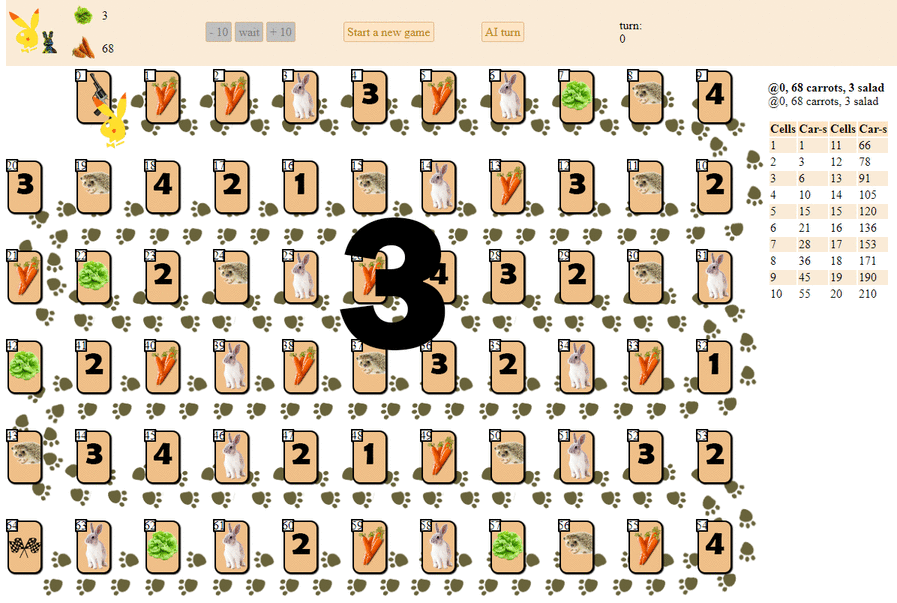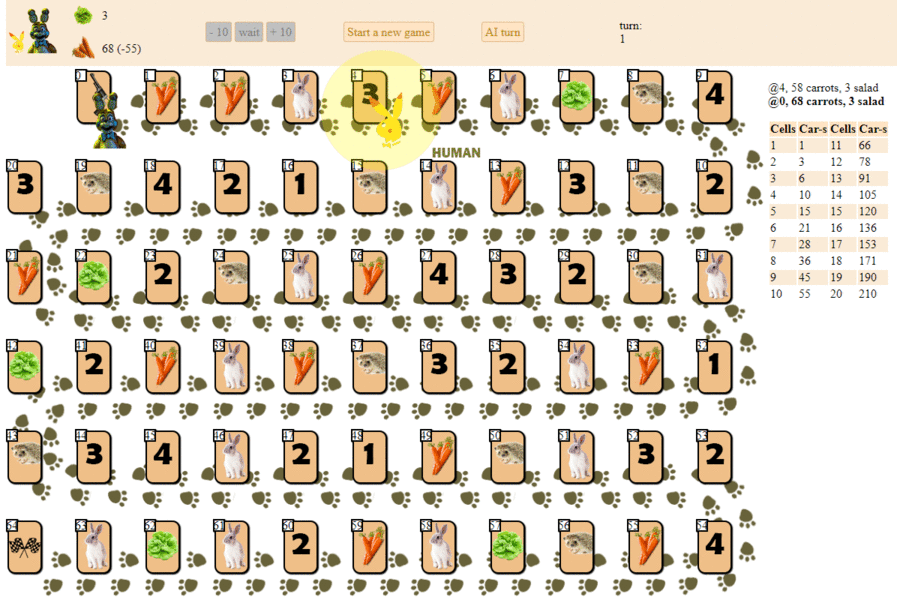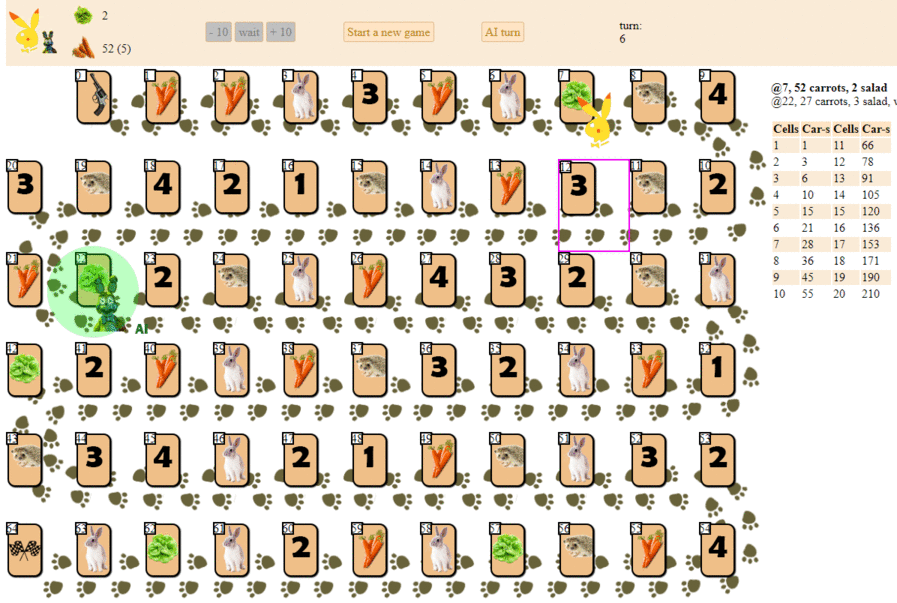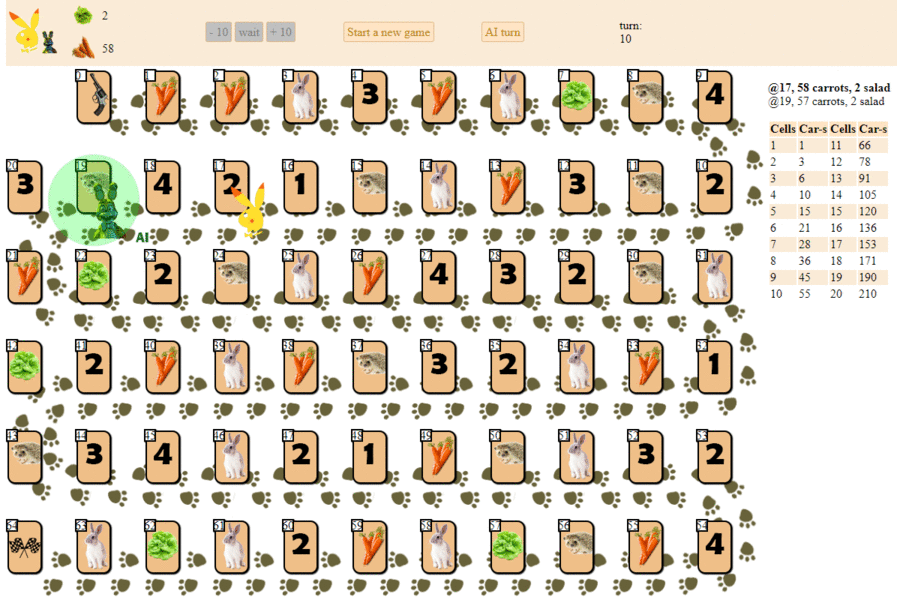
In principle, the debut is not so bad. However, one should not expect a good game from such an AI: by the middle of the game, the green “robot” starts to make repeated moves, and by the end it performs several iterations of moves forward - backward to the hedgehog, until finally it finishes. Finishes, partly due to chance, behind the player - a man for a dozen moves.
Implementation notes
The calculation of the assessment is managed by a special class - EstimationCalculator. Position evaluation functions for carrot-lettuce cards are loaded into arrays in the static constructor of the calculator class. At the input, the position estimation method receives the position object itself and the player's index, from the “point of view” of which the position is estimated by the algorithm. That is, the same game position may receive several different ratings, depending on which player is considered to be virtual points.
Decision tree and Minimax algorithm
We use the decision algorithm in the antagonistic game “Minimax”. Very well, in my opinion, the algorithm is described in this post (translation) .
Teach the program to “look in” a few moves ahead. Suppose that from the current position (and the algorithm doesn’t matter about the prehistory — as we remember, the program functions as a Moore machine gun ), numbered 1, the program can take two turns. We will get two possible positions, 2 and 3. Next comes the turn of the player - the person (in the general case - the enemy). From the 2nd position, the opponent has 3 moves, from the third - only two moves. Next, the turn to make a move again falls to the program, which, in total, can make 10 moves out of 5 possible positions:
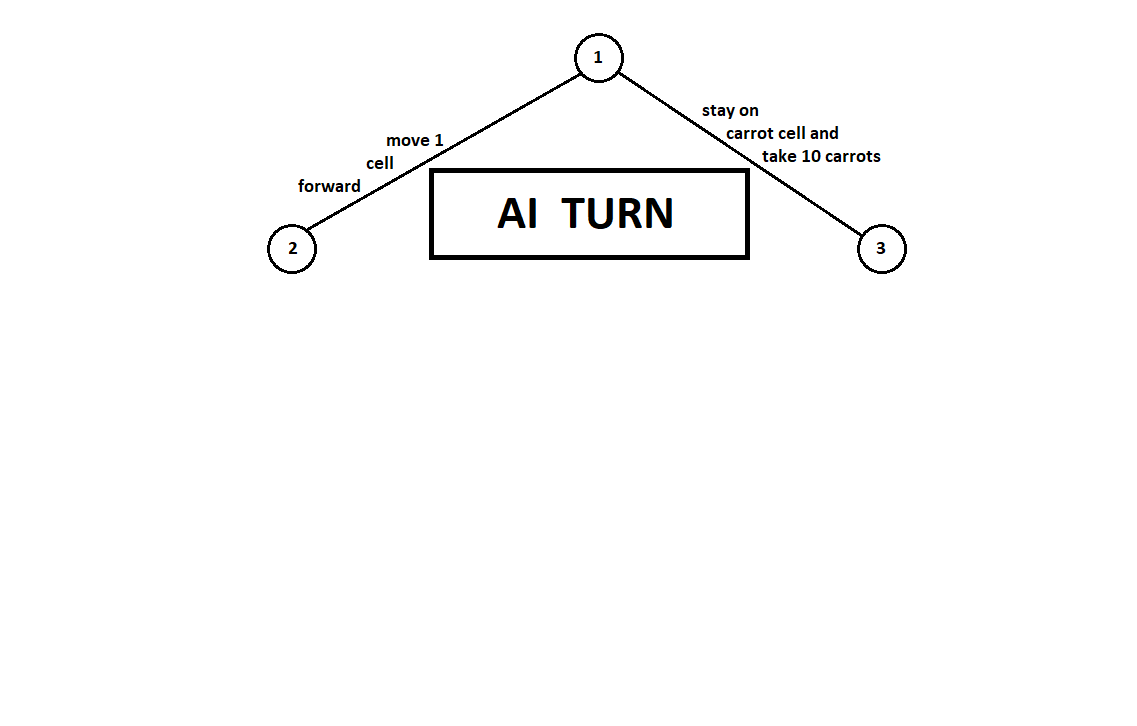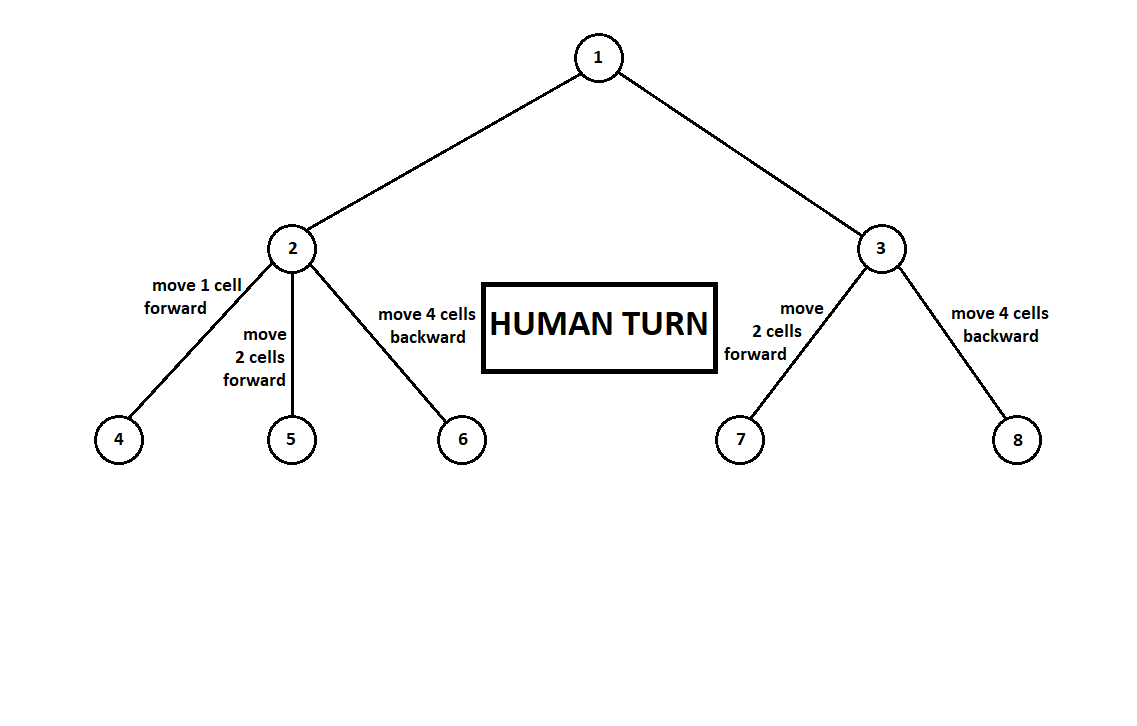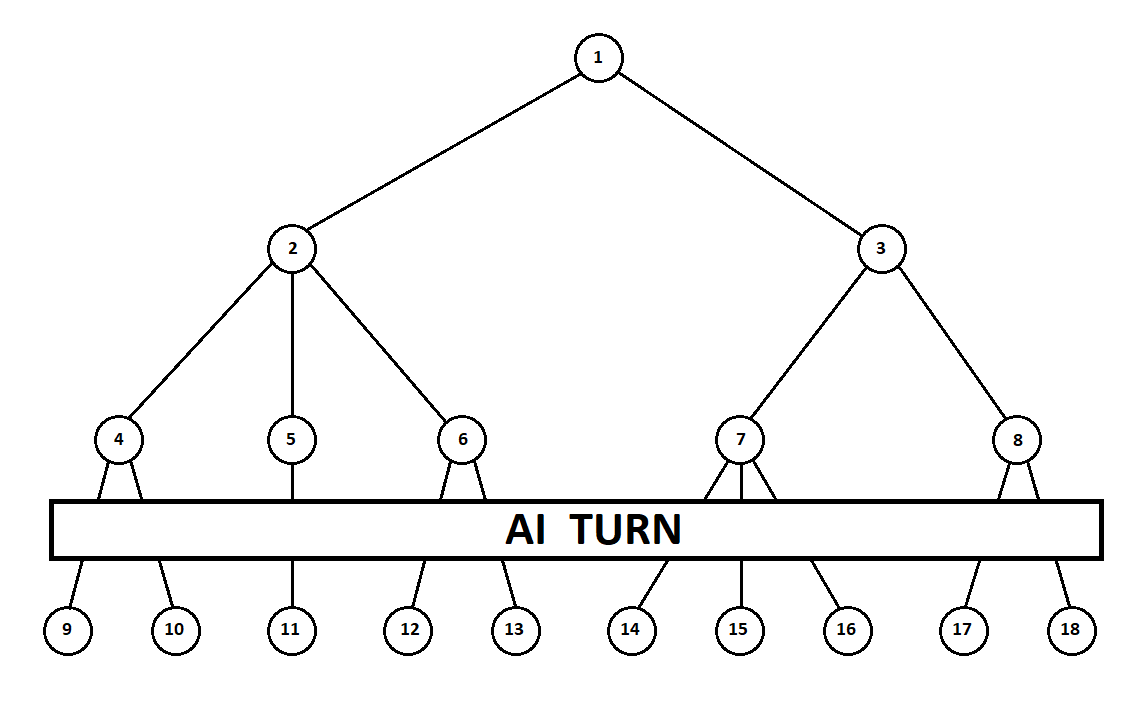
Suppose that after the second move of the computer the game ends and each of the positions obtained is evaluated from the point of view of the first and second players. And the evaluation algorithm we have already implemented. Let us evaluate each of the final positions (leaves of a tree 9 ... 18) in the form of a vector
where
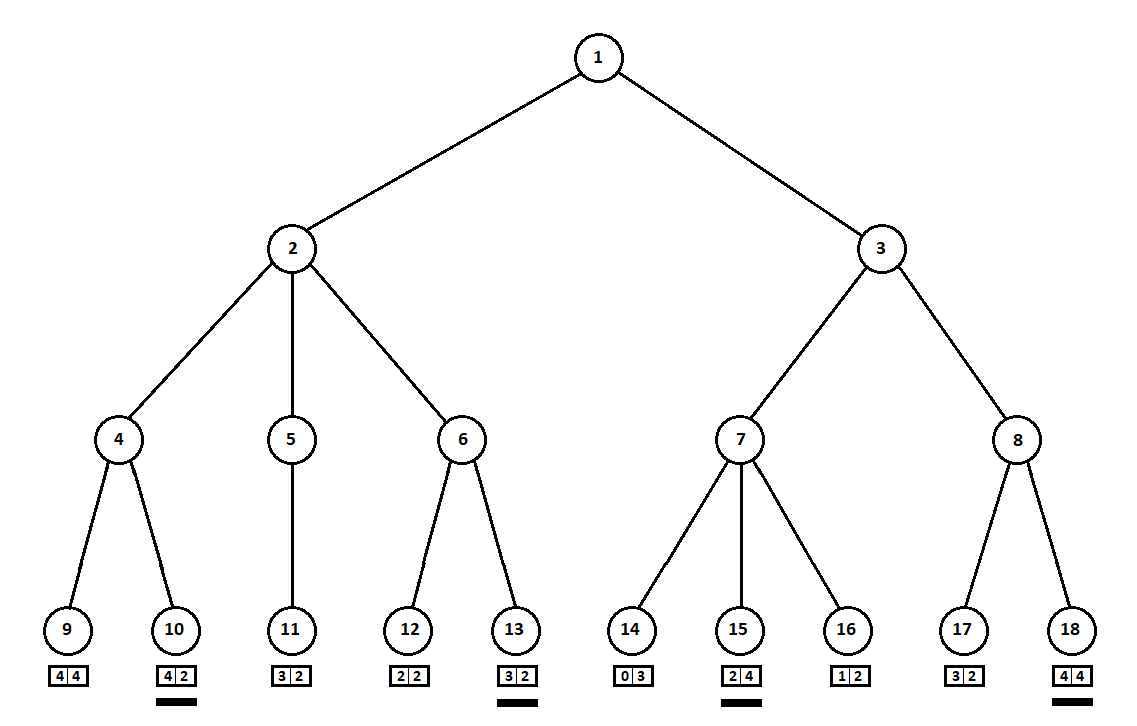
Since the last move is made by a computer, he will obviously choose options in each of the subtrees ([9, 10], [11], [12, 13], [14, 15, 16], [17, 18]) the one that gives him the best estimate. The question immediately arises: on what basis to choose the “best” position?
For example, there are two moves, after which we have positions with estimates [5; 5] and [2; one]. Evaluates the first player. Two alternatives are obvious:
- the choice of the position with the maximum absolute value of the i-th score for the i-th player. In other words, the noble racer Leslie, eager for victory, without looking at the competition. In this case, the position with the estimate will be selected [5; five].
- choosing a position with a maximum rating relative to that of competitors is a cunning professor Faith, who does not miss the opportunity to cause a dirty trick to the enemy. For example, deliberately lagging behind the player who plans to start from the second position. A position with an estimate of [2; one].
In my software implementation, I made an evaluation selection algorithm (a function that maps the evaluation vector to a scalar value for the i-th player) as a configurable parameter. Further tests showed, to some surprise to me, the superiority of the first strategy — the choice of position by the maximum absolute value.
Features of software implementation
If the first choice of choosing the best grade is specified in the AI settings (of the TurnMaker class), the code of the corresponding method takes the form:
The second method - maximum relative to the positions of competitors - is implemented a little more complicated:
intContractEstimateByAbsMax(int[] estimationVector, int playerIndex)
{
return estimationVector[playerIndex];
}
The second method - maximum relative to the positions of competitors - is implemented a little more complicated:
intContractEstimateByRelativeNumber(int[]eVector, int player)
{
int? min = null;
var pVal = eVector[player];
for (var i = 0; i < eVector.Length; i++)
{
if (i == player) continue;
var val = pVal - eVector[i];
if (!min.HasValue || min.Value > val)
min = val;
}
return min.Value;
}
The selected estimates (underlined in the figure) are moved up one level. Now, the opponent will have to choose a position, knowing which subsequent position the algorithm will choose:
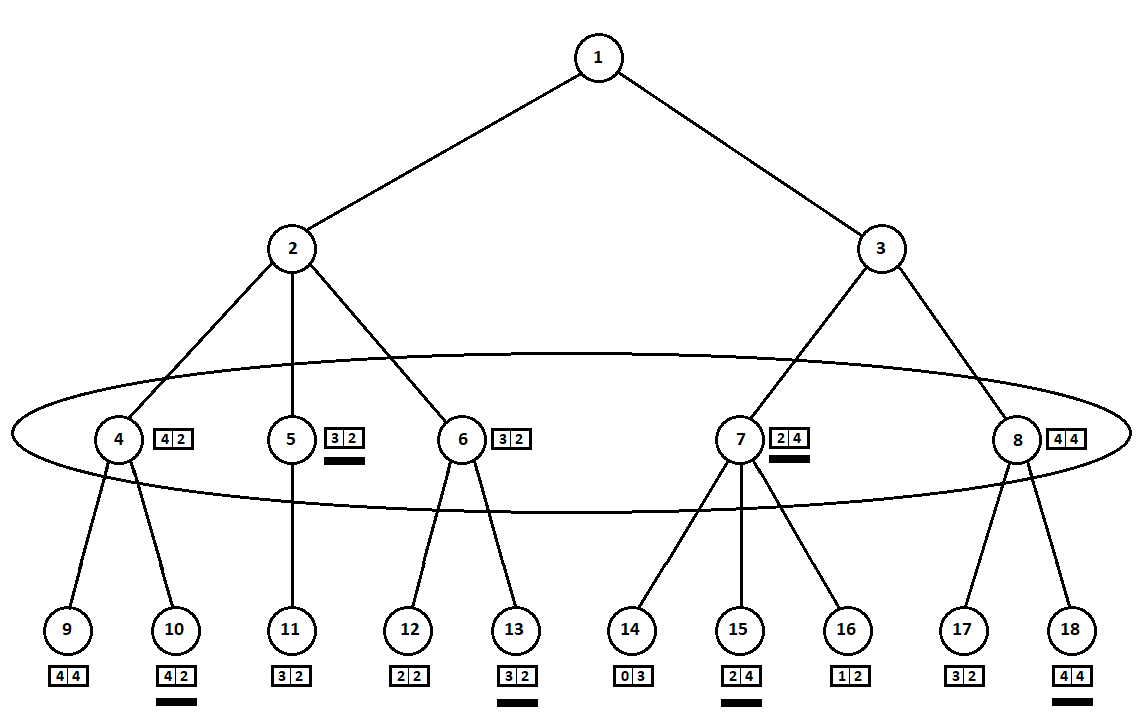
The adversary will obviously choose the position with the best estimate for himself (the one where the second coordinate of the vector takes the greatest value). These ratings are again underlined in the graph.
Finally, we return to the very first move. He chooses a computer, and he gives preference to the move with the greatest first coordinate of the vector:
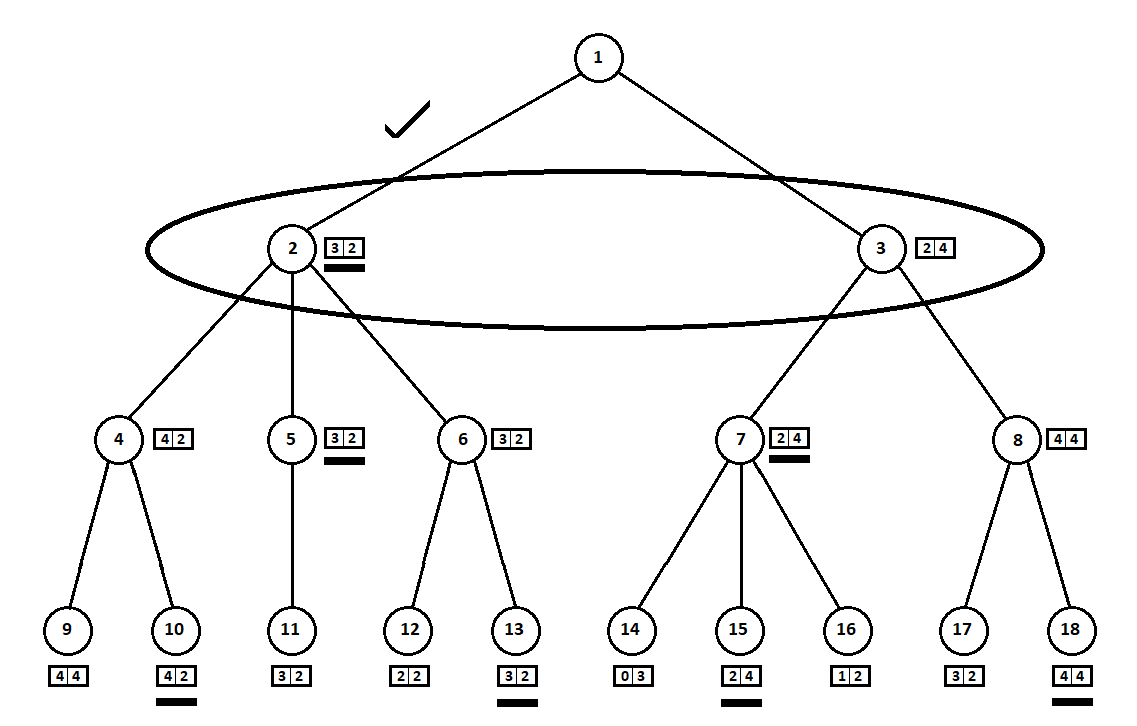
Thus, the problem is solved - a quasi-optimal move is found. Suppose a heuristic estimate in the tree leaf positions is 100% indicating a future winner. Then our algorithm will definitely choose the best possible move.
However, the heuristic estimate is 100% accurate only when the final position of the game is evaluated - one (or several) players finished, the winner was determined. Therefore, having the opportunity to look at N moves ahead - as much as it takes to win rivals equal in strength, you can choose the optimal move.
But a typical game for 2 players lasts on average about 30 - 40 moves (for three players - about 60 moves, etc.). From each position a player can usually make about 8 moves. Therefore, a full tree of possible positions for 30 moves will consist of approximately
In practice, building and “parsing” a tree from ~ 100,000 positions on my PC takes about 300 milliseconds. What gives us a limit on the depth of the tree in 7 - 8 levels (moves), if we want to wait for the computer to respond only less than a second.
Features of software implementation
Для построения дерева позиций и отыскания лучшего хода, очевидно, потребуется рекурсивный метод. На входе метода — текущая позиция (в которой, как мы помним, уже указан игрок, совершающий ход) и текущий уровень дерева (номер хода). Как только мы опускаемся на максимальный допустимый настройками алгоритма уровень, функция возвращает вектор эвристической оценки позиции с “точки зрения” каждого из игроков.
Важное дополнение: спуск ниже по дереву необходимо прекратить также в том случае, когда текущий игрок финишировал. Иначе (если выбран алгоритм отбора лучшей позиции относительно позиций других игроков) программа может довольно долго “топтаться” у финиша, “глумясь” над соперником. К тому же, так мы немного уменьшим размеры дерева в эндшпиле.
Если мы еще не находимся на предельном уровне рекурсии, то выбираем возможные ходы, создаем новую позицию для каждого хода и передаем ее в рекурсивный вызов текущего метода.
Важное дополнение: спуск ниже по дереву необходимо прекратить также в том случае, когда текущий игрок финишировал. Иначе (если выбран алгоритм отбора лучшей позиции относительно позиций других игроков) программа может довольно долго “топтаться” у финиша, “глумясь” над соперником. К тому же, так мы немного уменьшим размеры дерева в эндшпиле.
Если мы еще не находимся на предельном уровне рекурсии, то выбираем возможные ходы, создаем новую позицию для каждого хода и передаем ее в рекурсивный вызов текущего метода.
Why “Minimax”?
В оригинальной трактовке игроков всегда двое. Программа рассчитывает оценку исключительно с позиции первого игрока. Соответственно, при выборе “лучшей” позиции, игрок с индексом 0 ищет позицию с максимумом оценки, игрок с индексом 1 — с минимумом.
В нашем случае оценка должна быть вектором, чтобы каждый из N игроков мог оценить ее со своей “точки зрения”, по мере того как оценка поднимается вверх по дереву.
В нашем случае оценка должна быть вектором, чтобы каждый из N игроков мог оценить ее со своей “точки зрения”, по мере того как оценка поднимается вверх по дереву.
Tuning AI
My practice of playing against the computer has shown that the algorithm is not so bad, but still so far inferior to man. I decided to improve AI in two ways:
- optimize the construction / passage of the decision tree,
- improve heuristics.
Optimization algorithm Minimax
In the example above, we could refuse to consider position 8 and “save” 2 - 3 tree tops: We go
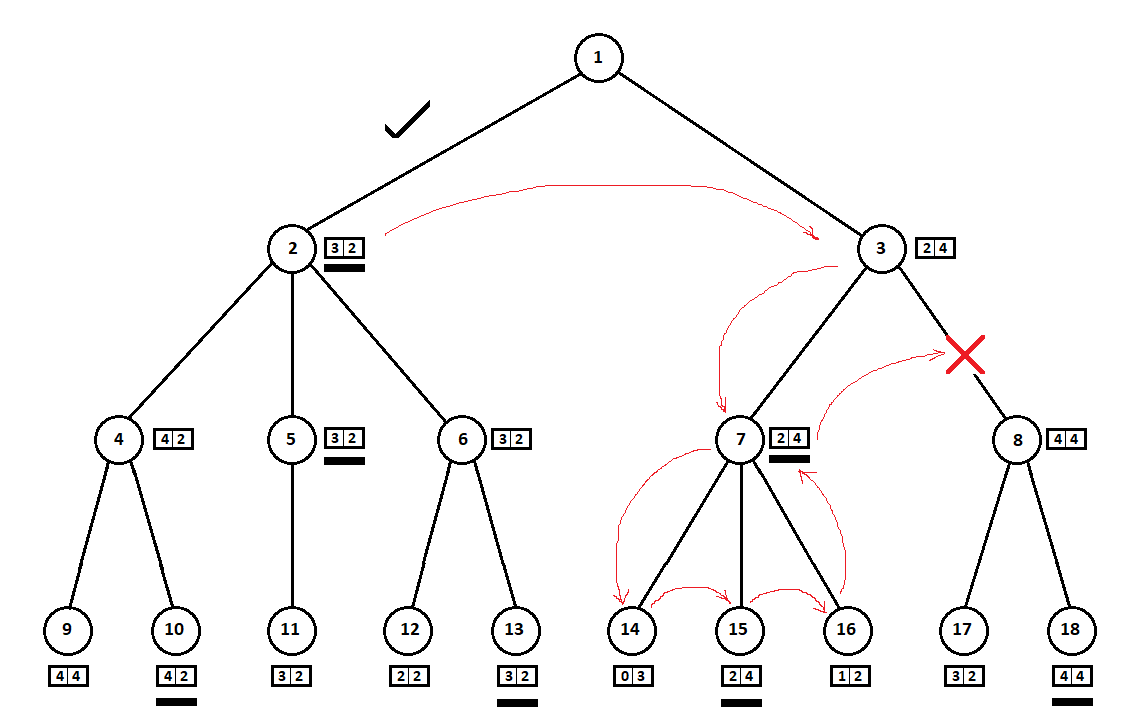
around the tree from top to bottom, from left to right. Bypassing the subtree starting at position 2, we derived the best estimate for move 1 -> 2: [3, 2]. By going around the subtree rooted at position 7, we determined the current (best for move 3 -> 7) grade: [2, 4]. From the point of view of the computer (first player), the rating [2, 4] is worse than the rating [3, 2]. And since the opponent of the computer chooses the move from position 3, whatever the estimate for position 8, the final assessment for position 3 will be a priori worse than the estimate obtained for the third position. Accordingly, the subtree rooted at position 8 can be not built or evaluated.
The optimized version of the Minimax algorithm, which allows to cut off extra subtrees, is calledalpha-beta clipping algorithm . To implement this algorithm, minor modifications to the source code will be required.
Features of software implementation
в метод CalcEstimate класса TurnMaker дополнительно передаются два целочисленных параметра — alpha, равный изначально int.MinValue и beta, равный int.MaxValue. Далее, после получения оценки текущего рассматриваемого хода, выполняется псевдокод вида:
e = вектор_оценок[0] // оценка текущей позиции для первого игрокаесли (ход первого игрока)
если (e > alpha)
alpha = e
иначеесли (e < beta)
beta = e
если (beta <= alpha)
завершить перебор возможных ходов
An important feature of the software implementation
метод альфа-бета отсечения по-определению приводит к тому же решению, что и “чистый” алгоритм Минимакс. Чтобы проверить, не изменилась ли логика принятия решения (а точнее, результаты — ходы), я написал юнит-тест, в котором робот совершал по 8 ходов для каждого из 2-х соперников (16 ходов всего) и сохранял полученную серию ходов — с отключенной опцией отсечения.
Затем, в том же тесте, процедура повторялась при включенной опции отсечения. После чего последовательности ходов сравнивались. Расхождение в ходах говорит об ошибке реализации алгоритма альфа-бета отсечения (тест провален).
Затем, в том же тесте, процедура повторялась при включенной опции отсечения. После чего последовательности ходов сравнивались. Расхождение в ходах говорит об ошибке реализации алгоритма альфа-бета отсечения (тест провален).
Small optimization of alpha-beta clipping algorithm
With the cut-off option enabled in the AI settings, the number of vertices in the position tree decreased by an average of 3 times. This result can be slightly improved.
In the above example:

so successfully “coincided” that, before the subtree with the top in position 3, we looked at the subtree with the top in position 2. If the order were different, we could start with the “worst” subtree and not conclude that meaning in the consideration of the next position.
As a rule, clipping on a tree is more “economical”, the vertices of which are on the same level (i.e., all possible moves from the i-position) are already sorted by the current position estimate (without looking inwards). In other words, we assume that from a better (from the point of view of heuristics) progress, there is a greater likelihood of obtaining a better final grade. Thus, we are, with some probability, sorting the tree so that the “best” subtree will be considered before the “worst”, which will allow cutting off more options.
Evaluating the current position is a costly procedure. If before it was enough for us to evaluate only the terminal positions (leaves), now the estimate is made for all tree tops. However, as the tests showed, the total number of assessments made was still somewhat less than in the variant without the initial sorting of possible moves.
Features of software implementation
Алгоритм альфа-бета отсечения возвращает тот же ход, что и исходный алгоритм Минимакс. Это проверяет написанный нами юнит-тест, сравнивающий две последовательности ходов (для алгоритма с отсечением и без). Альфа-бета отсечение с сортировкой, в общем случае, может указать на другой ход в качестве квазиоптимального.
Чтобы протестировать корректную работу модифицированного алгоритма, нужен новый тест. Несмотря на модификацию, алгоритм с сортировкой должен выдавать ровно тот же итоговый вектор оценки ([3, 2] в примере на рисунке), что и алгоритм без сортировки, что и исходный алгоритм Минимакс.
В тесте я создал серию пробных позиций и выбрал из каждой по “лучшему” ходу, включая и отключая опцию сортировки. После чего сравнил полученные двумя способами вектора оценки.
Чтобы протестировать корректную работу модифицированного алгоритма, нужен новый тест. Несмотря на модификацию, алгоритм с сортировкой должен выдавать ровно тот же итоговый вектор оценки ([3, 2] в примере на рисунке), что и алгоритм без сортировки, что и исходный алгоритм Минимакс.
В тесте я создал серию пробных позиций и выбрал из каждой по “лучшему” ходу, включая и отключая опцию сортировки. После чего сравнил полученные двумя способами вектора оценки.
Additionally, since the positions for each of the possible moves in the current vertex of the tree are sorted by heuristic evaluation, the idea suggests itself to immediately discard some of the worst options. For example, a chess player may consider a move in which he substitutes his own rook under the blow of a pawn. However, “unwinding” the situation deeper by 3, 4 ... moves forward, he immediately marks the options when, for example, the enemy submits his queen for an elephant.
In the AI settings, I set the “cutoff worst case” vector. For example, a vector of the form [0, 0, 8, 8, 4] means that:
- Looking at one [0] and two [0] steps forward, the program will consider all possible moves, because 0 means no clipping,
- looking at three [8] and four [8] steps forward, the program will consider up to 8 “best” moves, leading from the next position, inclusive,
- Looking at five or more steps forward [4], the program will appreciate no more than 4 “best” moves.
With enabled sorting for the alpha-beta cut-off algorithm and a similar vector in the cut-off settings, the program began to spend about 300 milliseconds on the choice of a quasi-optimal move, “going deeper” 8 steps ahead.
Optimization of heuristics
Despite the decent number of vertices being picked in the tree and the “deep” looking ahead in search of a quasi-optimal move, AI had several weak points. I have defined one of them as a “ hare trap ”.
Hare trap
Клетка зайца вносит в игру элемент случайности. Как правило (в 8 — 10 случаях из 15), случайность оказывается неприятной для игрока. Поэтому я определил следующие “эффекты” для клетки зайца при оценке и построении дерева позиций (не непосредственно в игре!):
Однако идея со штрафом на практике не сработала. Приведу пример:
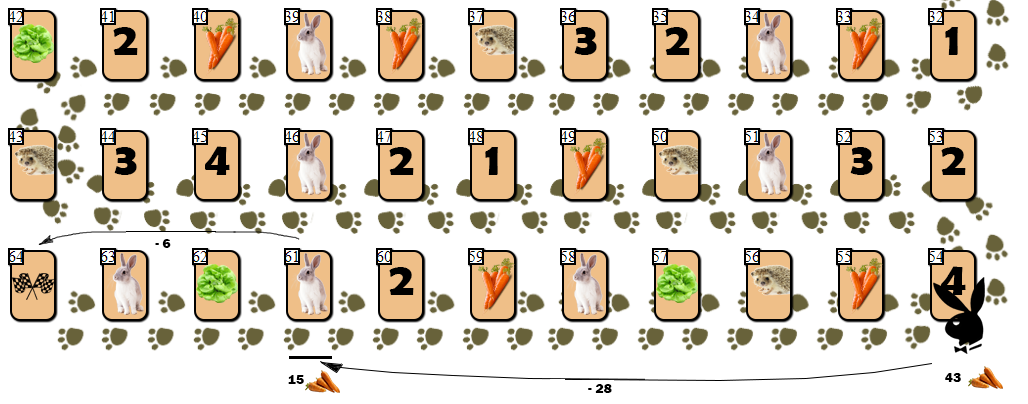
У игрока на клетке 54 недостаточно морковки (43), чтобы финишировать за один ход — ход на 10 клеток вперед потребовал бы 55 морковок. Но AI, невзирая на штрафы, делает ход на клетку зайца (61), затрачивая 28 моркови. С расчетом в дальнейшем совершить победный ход, потратив еще 6 морковок и сведя общее количество моркови на руках к 9 (допустимо финишировать с запасом не более 10 морковок).
Однако в игре, где конкретную карту зайца определяет случай (генератор БПСЧ), заяц с немалой вероятностью получит на руки дополнительную морковь, избавляясь от которой будет вынужден совершить еще 4 — 6 ходов. Как так получилось, что, невзирая на большой штраф в оценке позиции с клеткой зайца, AI совершил такой неоправданно рискованный ход?
The fact is that the penalty is determined for one move , for one position. AI looks at several moves ahead. The penalty after the first move to the hare's cage does not participate in the final assessment, since it is followed by the move giving the highest possible rating. As a result, I solved the problem of the “hare trap” as follows:
the player’s move to one of the final hare cells equals the number of carrots in the player’s hands to 65 - this is one of the “effects” of the hare's cell, probably the worst possible in this situation. After such a step, the finishing move cannot be done, as there is an excess of carrots on the hands and a series of moves back, on a hedgehog, with a subsequent move (moves) forward to complete the game is required.
- ход на клетку зайца стабильно уменьшает количество морковок игрока на 7,
- при оценке позиции игрок, стоящий на клетке зайца, получает штраф. Штраф резко вырастает, если игрок, стоящий на клетке зайца, имеет возможность финишировать на следующем ходу.
Однако идея со штрафом на практике не сработала. Приведу пример:

У игрока на клетке 54 недостаточно морковки (43), чтобы финишировать за один ход — ход на 10 клеток вперед потребовал бы 55 морковок. Но AI, невзирая на штрафы, делает ход на клетку зайца (61), затрачивая 28 моркови. С расчетом в дальнейшем совершить победный ход, потратив еще 6 морковок и сведя общее количество моркови на руках к 9 (допустимо финишировать с запасом не более 10 морковок).
Однако в игре, где конкретную карту зайца определяет случай (генератор БПСЧ), заяц с немалой вероятностью получит на руки дополнительную морковь, избавляясь от которой будет вынужден совершить еще 4 — 6 ходов. Как так получилось, что, невзирая на большой штраф в оценке позиции с клеткой зайца, AI совершил такой неоправданно рискованный ход?
The fact is that the penalty is determined for one move , for one position. AI looks at several moves ahead. The penalty after the first move to the hare's cage does not participate in the final assessment, since it is followed by the move giving the highest possible rating. As a result, I solved the problem of the “hare trap” as follows:
the player’s move to one of the final hare cells equals the number of carrots in the player’s hands to 65 - this is one of the “effects” of the hare's cell, probably the worst possible in this situation. After such a step, the finishing move cannot be done, as there is an excess of carrots on the hands and a series of moves back, on a hedgehog, with a subsequent move (moves) forward to complete the game is required.
Correction factors
Earlier, in citing the heuristic estimation of the current position
E = Ks * S + Kc * C + Kp * P,
I mentioned, but did not describe the correction factors.
The fact is that both the formula itself and the sets of functions
How to evaluate the “adequacy” of the assessment? Evaluation is a dimensionless quantity, and it can only be compared with another estimate. I was able to come up with the only one way to refine the correction factors: I
put in the program a number of “sketches” stored in a CSV file with the data
45;26;2;f;29;19;0;f;2
...
This line literally means the following:
- the first player is on the 45th square, he has 26 cards of carrots and 2 cards of lettuce on his hands, the player does not miss the turn (f = false). The right turn is always the first player.
- The second player on the 29th cage with 19 cards of carrots and without lettuce cards does not miss the move.
- the number two means that, by “solving” the etude, I assumed that the second player is in a winning situation.
Having laid 20 etudes into the program, I “loaded” them in the game web-client, and then analyzed each etude. Analyzing the etude, I alternately made moves for each of the players, until I decided on the “winner”. After finishing the assessment, I sent it to a special team on the server.
Estimating 20 etudes (of course, it would be worthwhile to sort them out more), I evaluated each etude by the program. When evaluating in turn, the values of each of the correction factors were selected, from 0.5 to 2 with a step of 0.1 - total
In the end, I chose those triples for which the percentage of “hits” was maximum (16 out of 20). About 250 of 4096 vectors came out, from which I selected the “best”, again, “by eye”, and set it in the AI settings.
Results
As a result, I received a work program, which, as a rule, beats me in a one-on-one version against the computer. Serious statistics of wins and losses for the current version of the program has not yet accumulated. Perhaps the subsequent easy tuning AI will make my victories impossible. Or almost impossible, since the hare cell factor still remains.
For example, in the evaluation logic (absolute maximum or maximum relative to other players), I would definitely try an intermediate option. As a minimum, if the absolute value of the i-th player is equal, it is reasonable to choose the move leading to a position with a higher relative value of the score (a hybrid of the noble Leslie and the cunning Feith).
The program is quite workable for the version with 3 players. However, there are suspicions that the “quality” of AI moves for a game with 3 players is lower than for a game with two players. However, in the course of the last test, I lost the computer — perhaps through carelessness, casually evaluating the amount of carrots on my hands and coming to the finish line with an excess of “fuel”.
So far, the further development of AI hinders the absence of a person - a “tester,” that is, a living opponent of a computer “genius.” I myself have played enough in the Hare and the Hedgehog to nausea and have to stop at the current stage.
→ Link to source repository
