learnopengl. Lesson 1.7 - Transformations
- Transfer
- Tutorial
 Now we know how to create objects, color them and apply textures to them, but they are still quite boring because they are static objects. We can try to make them move by changing the coordinates of the vertices for each frame, but this is rather dreary and requires processor calculations. There is a much more convenient way to perform transformations on an object - this is the use of matrices. But this does not mean that we will now talk about kung fu and the artificial digital world.
Now we know how to create objects, color them and apply textures to them, but they are still quite boring because they are static objects. We can try to make them move by changing the coordinates of the vertices for each frame, but this is rather dreary and requires processor calculations. There is a much more convenient way to perform transformations on an object - this is the use of matrices. But this does not mean that we will now talk about kung fu and the artificial digital world.
Part 1. Getting Started
- Opengl
- Window creation
- Hello window
- Hello triangle
- Shaders
- Textures
- Transformations
- Coordinate systems
- Camera
Part 2. Basic lighting
Part 3. Download 3D models
Part 4. Advanced OpenGL Features
- Depth test
- Stencil test
- Color mixing
- Clipping faces
- Frame buffer
- Cubic cards
- Advanced data handling
- Advanced GLSL
- Geometric shader
- Instancing
- Smoothing
Part 5. Advanced Lighting
Matrices are very powerful mathematical constructions that at first scare, but if you get used to them, they will immediately become extremely useful. When discussing matrices, you also need to go a little deeper into mathematics. Also, for more mathematically inclined readers, I will leave links to additional resources on this topic.
Be that as it may, in order to fully understand the transformations, we must first of all deal with the vectors. The main task of this chapter is to give you the basic mathematical knowledge that we will need later.
Vectors
In its simplest definition, vectors are nothing more than directions. A vector can have direction and magnitude (also sometimes called modulus or length). You can imagine vectors as directions on the treasure map: “Take 10 steps to the left, now 3 steps to the north and now 5 steps to the right”. In this example, “left” is the direction, and “10 steps” is the length of the vector. The directions on this treasure map are made up of 3 vectors. Vectors can have any dimension, but most often two-component and four-component vectors are used. If the vector is two-component, then it describes the direction on the plane (or on a 2D chart), if the vector is three-component, then it describes the direction in the three-dimensional world.
Below you can see 3 vectors, each of which is represented in the form of (x, y) as arrows on a 2D chart. Since it is more intuitive to represent vectors in 2D (than in 3D), you can think of 2D vectors as 3D vectors, but with a z-coordinate of zero. As long as the vector describes the direction, the position of the vector does not change its value. On the graph you can see that the vectors v and w are the same, although they differ from the position:
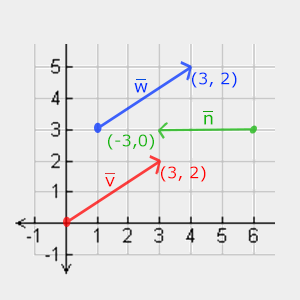
When mathematicians describe vectors, they prefer to use lowercase characters with a small dash on top. Example:
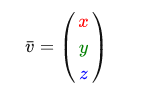
Since vectors often describe the direction, it is sometimes difficult to represent them in the form of a position. Usually we visualize the vector as follows: we set the center to (0, 0, 0) , and then indicate the direction described by the point. Thus, a positional vector is obtained (we can also take another point as the center, and then say “This vector points to a point in space from this point”). The position vector (3, 5) will point to the point (3, 5) on the graph with the base (0, 0) . Using vectors, we can describe both directions and positions in two-dimensional and three-dimensional spaces.
We can also perform some mathematical operations on vectors.
Scalar vector operations
A scalar is a single number (or a one-component vector if you want to continue working with vectors). During addition / subtraction / multiplication or division of a vector by a scalar, we simply add / subtract / multiply or divide each element of the vector by this scalar. Example:
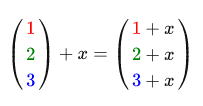
Where instead of addition there can be subtraction, multiplication or division.
Reverse vector
The inverse (negation) of a vector is the receipt of a vector whose direction is opposite to the original. The inverse vector for a vector pointing to the northeast will be a vector pointing to the southwest. To invert a vector, we simply multiply the vector by -1. Example:

Addition and Subtraction
The addition of two vectors is done componentwise . Example:
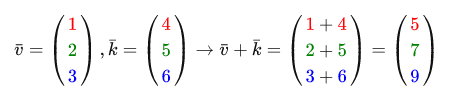
Visually, the sum of the vectors v = (4,2) and k = (1,2) looks like this:
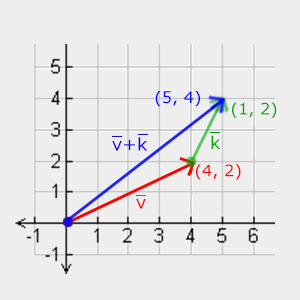
As with ordinary addition and subtraction, subtracting vectors is also addition, but with the inverse second vector:
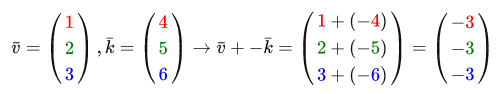
Subtracting vectors from each other generate a vector, which is the difference in the positions of the operands:
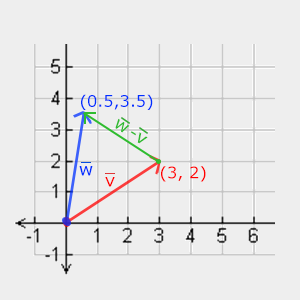
Length
To obtain the length (module) of the vector, we use the Pythagorean theorem , which you may remember from school. A vector forms a triangle if its components are represented as sides of a triangle:

Since the length of the sides (x, y) is known, and we want to know the length of the hypotenuse, we do this as follows:

Where || v || Is the length of the vector v . Such a formula can be easily extended in 3D by adding z ^ 2 . Length calculation example:
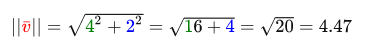
Calculated value: 4.47
There is also a special kind of vectors called unit vectors . A feature of such vectors is that their length is always 1. We can transform any vector into a unit by dividing this vector by its length:
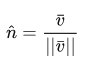
Such a vector is called normalized . Single vectors are indicated with a small roof over the letter. It is also easier to work with them, since we only have to care about the direction of such a vector.
Multiplication of vector by vector
Multiplication of two vectors is rather strange. Normal multiplication is not applicable, because it does not have visual meaning, but we have 2 specific approaches from which you can choose during the multiplication: the first is a scalar product that is depicted as a point, and the second is a vector product that is depicted as a cross.
Scalar product
The scalar product of two vectors is equivalent to the scalar product of the lengths of these vectors multiplied by the cosine of the angle between them. If this sentence has confused you, then look at the formula:
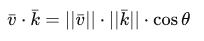
Where the angle between the vectors is described as theta . Why might this be interesting? Well, imagine if the vectors v and k are unit vectors. Accordingly, the formula is reduced to:

Now the scalar product determines only the angle between two vectors. You may remember that the cos function becomes 0, with an angle of 90 degrees and 1 with an angle of 0. This makes it easy to check whether the vectors are orthogonal or parallel to each other (orthogonality means that the vectors are rectangular). If you want to know more about sin or cosine , then I recommend the Khan Academy video about basic trigonometry.
You can also calculate the angle between two non-unit vectors, but for this you will have to divide the result by the lengths of these vectors in order to stay only with cos .
So how do you count a scalar product? The scalar product is the multiplication of the components of the vectors and the subsequent addition of the results. Example:

To calculate the angle between the vectors, we need to invert the cosine function (cos ^ -1) in this case - it is 143.1 degrees. Thus, we effectively calculated the angle between these two vectors. Scalar work is very useful when working with light.
Vector artwork
A vector product is possible only in three-dimensional space and takes two non-parallel vectors as input, and returns a vector that is orthogonal to the input. If the input vectors are orthogonal to each other, then the vector product will create 3 orthogonal vectors. Next, you'll find out why this might be helpful. The following image shows how it looks in three-dimensional space:
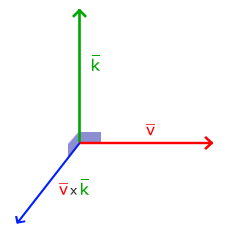
Unlike other operations, a vector product is not very intuitive without going deep into linear algebra, so it’s better to just remember the formula. Below is the vector product between two orthogonal vectors A and B.
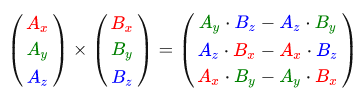
As you can see, this formula does not make much sense. In any case, after all these steps, you will receive a vector that will be orthogonal to the input.
Matrices
Now, after we have discussed almost everything about vectors, it's time to delve into the matrices. A matrix is usually quadrangular from a set of numbers, characters and / or expressions. Here is an example of a 2x3 matrix:
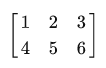
The matrix elements are accessed using (i, j) , where i is a row and j is a column. This is why the matrix above is called 2x3 (3 columns and 2 rows). Such a system is the reverse of that used in 2D graphs (x, y) . To get the value 4 from the matrix above, we must specify the index (2, 1) (second row, first column).
Matrices, in fact, are nothing more than quadrangular arrays of mathematical expressions. They also have a very nice set of mathematical properties and, like vectors, they have several operations - addition, subtraction and multiplication.
Addition and Subtraction
Addition of a matrix with a scalar is performed as follows:
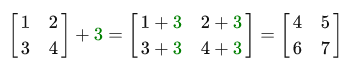
The scalar is simply added to all elements of the matrix. The same thing happens when subtracting:
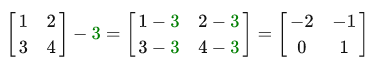
Addition and subtraction between two matrices is performed element-by-element. Thus, addition and subtraction operations can only be applied to matrices of the same size. Example:
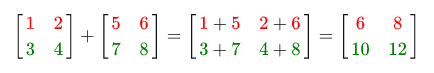
The same thing, only with subtraction:
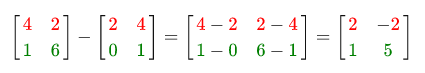
Scalar matrix multiplication
As well as addition and subtraction, the matrix is multiplied by a scalar by multiplying each matrix element by a scalar. Example:

Matrix multiplication
Matrix multiplication is not very difficult, but not so simple either. Multiplication has several limitations:
- You can only multiply matrices, where the number of columns of the first matches the number of rows of the second matrix.
- Matrix multiplication is not commutative. A * B! = B * A.
Here is an example of multiplying two 2x2 matrices:

Now, maybe you’re trying to understand what’s going on here? Matrix multiplication is a combination of normal multiplication and addition using the rows of the left matrix with the columns of the right matrix. The following image should bring a little clarity:

At the beginning we take the top row of the left matrix and the left column of the right matrix. The row and column selected by us determines which element of the resulting matrix we are going to calculate. If we took the first row of the left matrix, then we are going to work with the top row of the resulting matrix, then we select the column in the right matrix, it determines which column of the resulting matrix we are working with. To calculate the bottom-right element, we must select the bottom row of the left matrix and the right column of the right matrix.
To calculate the resulting value, we multiply the elements of the row and column using ordinary multiplication. The multiplication results are then added up and we get the result. This is where the first limitation comes from.
The result is a matrix of size (n, m) , where n is the number of rows in the left matrix, and m is the number of columns in the right matrix.
If you have a problem - then do not worry. Just keep calculating with your hands and come back to this lesson when difficulties arise. Soon matrix multiplication will be on the automaton.
Let's close the question of matrix multiplication with one big example. Colors are used to represent the algorithm. For training, try to calculate the result yourself, and then compare with the result in the example.

As you can see, matrix multiplication is a rather dreary process with a lot of places where you can make a mistake. And these problems only grow with increasing size. If you are still craving more mathematical properties of matrices, I highly recommend the Khan Academy video .
Multiplication of a matrix by a vector
We have already used vectors in past lessons. We used them to represent positions, colors, and texture coordinates. Now let's go a little deeper into the rabbit hole and tell you that the vector is really just an Nx1 matrix, where N is the number of vector components. If you think about it a little, it makes sense. Vectors, just like matrices, are an array of numbers, but with only 1 column. And how can this information help us? Well, if we have a matrix MxN, we can multiply it by Nx1 vector, since the number of columns in the matrix is equal to the number of rows of the vector.
But why should we even be able to multiply the matrix by a vector? Quite a lot of different 3D / 2D transformations can be performed by multiplying the matrix by a vector to obtain a modified vector. If you are still not sure that you fully understand the text above, here are a few examples:
Unit matrix
OpenGL typically works with 4x4 transformation matrices for the reason that most vectors have 4 components. The simplest transformation matrix that can be discussed is the identity matrix . The identity matrix is an NxN matrix filled with zeros, but with 1 diagonally. As you can see, this matrix does not change the vector at all:
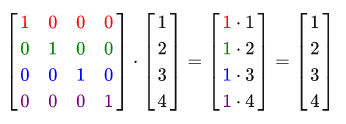
The vector looks untouched. This becomes apparent from the rules of multiplication: the first resulting element is each element of the first row of the matrix, multiplied by each element of the vector. Since each element of the string is 0, except for the first one, we get 1 * 1 + 0 * 2 + 0 * 3 + 0 * 4 = 1. The same applies to the remaining 3 elements of the vector.
You may ask, why at all might a transformation matrix be needed that does not transform anything? The identity matrix is often the starting point for generating other transformation matrices, and if we delve into linear algebra, it is also a very convenient matrix for proving theorems and solving linear equations.
Scaling matrix
When we scale the vector, we increase the length of the arrow by the amount of scaling, preserving the direction. While we work in 2 or 3 dimensions, we can determine the scaling by a vector of 2 or 3 quantities, each of which scales one of the axes (x, y or z) .
Let's try to scale the vector v = (3,2) . We will scale the vector along the x axis by 0.5 , which will make it 2 times narrower; and scale the vector along the y axis by 2 , which will increase the height by 2 times. Let's see what it will look like if we scale the vector by (0.5, 2). We write the result in the form s .
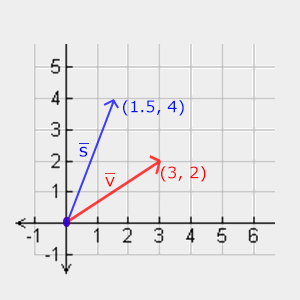
Remember that OpenGL often works in 3D space, so for 2D you can leave the Z coordinate equal to 1. The scaling operation that we just performed is heterogeneous , because the scaling value for each axis varies. If the scaling value were the same, then such a transformation is called homogeneous .
Let's build a transformation matrix that will scale for us. We have already seen on the unit matrix that the diagonal element will be multiplied by the corresponding element of the vector. What if we replace the units in the identity matrix with triples? In this case, we multiply all the elements of the vector by this value. Accordingly, if we represent the scaling values as (S1, S2, S3), then we can determine the scaling matrix for any vector (x, y, z) :

Note that the 4th element of the vector is 1. This component is denoted by w and will then be used for other tasks.
Shift matrix
A shift is the process of adding one vector to another to obtain a new vector with a different position, that is, a shift of the vector based on the shift vector. We have already discussed the addition of vectors, so for you this will not be something new.
As well as with the scaling matrix in the 4x4 matrix there are several positions for performing the required operations, for shifting - these are the top 3 elements of the fourth column. If we represent the shear vector as (Tx, Ty, Tz), then we can define the shear matrix as follows:
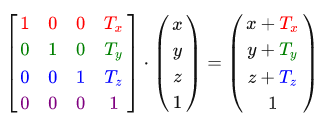
This works because all vector values are multiplied by the w components of the vector and added to the initial values. This would not be possible using 3x3 matrices.
Homogeneous coordinates
The component of the vector w is also called the homogeneous coordinate . To obtain a 3D vector from a homogeneous coordinate, we divide the x , y, and z coordinates by w . Usually they do not notice this, since w most of the time is 1.0. Using homogeneous coordinates has several advantages: they allow us to perform shifts on 3D vectors (without the w component this would not be possible) and in the next chapter we use the value w to create 3D visualizations.
Also, when the homogeneous coordinate is 0, then the vector is considered the direction vector, since a vector with component w equal to 0 cannot be shifted.
With the shift matrix, we can move objects in all 3 directions (x, y, z) , which makes this matrix extremely useful for our tasks.
Rotation matrix
The last couple of transformations were quite easy to understand and represent in 2D or 3D space, but the rotations are a bit more tricky. If you want to know how exactly these matrices are formed, then I recommend the Khan Academy video about linear algebra .
To begin, let's define what rotation of a vector is all about. Rotation in 2D and 3D is determined by the angle . The angle can be expressed in angles or in radians, in which the full revolution is 360 degrees or 2Pi, respectively. I prefer to work with degrees, as they are more logical for me.
Most rotational functions require an angle in radians, but the benefit of converting from one system to another is quite simple:
Degrees = radians * (180.0f / PI)
Radians = degrees * (PI / 180.0f)
Where PI is approximately 3.14159265359
Half circle rotation - requires 360/2 = 180 degrees rotation from us. Rotating 1/5 to the right requires us to rotate 360/5 = 72 degrees to the right. Here's an example of a regular 2D vector, where v is rotated 72 degrees to the right of k .
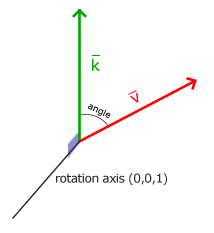
Rotation in 3D is described by the angle and axis of rotation . The angle determines how much the vector will be rotated about this axis. When rotating 2D vectors in the 3D world, for example, we will set the rotation axis - Z.
Using trigonometry, we can transform vectors into rotated angles. This is usually done with a cunning combination of sin and cos functions. A discussion of how transformation matrices are generated is beyond the scope of our lesson.
A rotation matrix is defined for each axis in 3D space, where the angle is shown as theta.
The rotation matrix around the X axis:
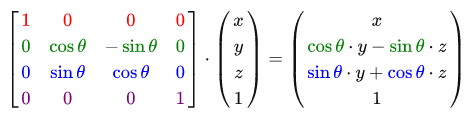
The rotation matrix around the Y axis:
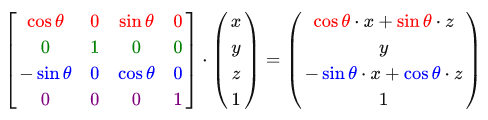
The rotation matrix around the Z axis:
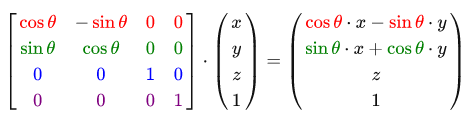
Using rotation matrices, we can rotate our vectors along one of three axes. You can also combine them, for example, at the beginning, turn along the X axis, and then along the Y axis. True, this approach will quickly lead to a problem called the Gimbal Lock problem. We will not go into details, but it is better to use rotation on a specific axis, for example (0.662, 0.2, 0.722) (note that this is a unit vector), instead of combining rotations on specific axes. The matrix for such transformations exists and it looks like this, where (Rx, Ry, Rz) is the axis of rotation:

Mathematical discussions about generating such a matrix are beyond the scope of this lesson. Just keep in mind that even such a matrix does not solve the problem of a hinged lock completely (it is simply more difficult to obtain). In order to completely solve this problem, we will have to work with rotations using quaternions, which are not only safer, but also much friendlier in terms of calculations. Be that as it may, the discussion of quaternions is reserved for a later lesson.
Matrix Combination
In order to achieve the maximum utility of using matrices for transformations, we must combine the transformation matrices into one matrix. Let's see if we can generate a transformation matrix that will include several transformations. For example, we have a vector (x, y, z) and we want to scale it 2 times and shift it by (1, 2, 3) . To do this, we need the scaling and displacement matrices. As a result, we get something like:
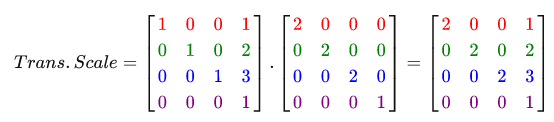
Note that during matrix multiplication, we first shift and then scale. Matrix multiplication is not commutative, which means that the order of multiplication is important. During matrix multiplication, the right matrix is multiplied by a vector, so you need to read the multiplications from right to left. It is recommended at the beginning to scale, then rotate and at the end to shift, during the union of the matrices, otherwise they can negate each other. For example, if at the beginning you perform a shift, and then scaling, then the shift matrix will also scale!
As a result, the transformation matrix is applied as follows:
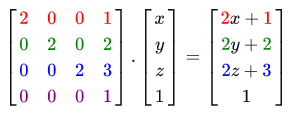
Well, the vector is scaled 2 times and is shifted by (1, 2, 3) .
On practice
After we have discussed the whole theory, it is time to put it into practice. OpenGL does not have built-in support for matrix or vector transformations, so we will have to use our own mathematical classes and functions. In these lessons, we abstract from subtle mathematical details and simply use ready-made mathematical libraries. Fortunately, there is already an easy-to-use and sharpened under OpenGL math library called GLM.
GLM
GLM is an abbreviation of Open GL M athematics. This library is the header, which means that we just need to connect the required header files. No need to bother with either linking or compilation. GLM can be downloaded from the official site . Copy the root directory with the header files into your includes folder and you can start.
Most GLM functionality can be found in 3 header files:
#include
#include
#include Let's see if we can apply our knowledge in the transformations to shift the vector (1, 0, 0) by (1, 1, 0) (note that we designated from glm :: vec4 with a homogeneous coordinate equal to 1.0):
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;In the beginning, we created a vector called vec using the GLM built-in vector class. Then we define mat4 , which is a 4x4 unit matrix. Then we create the transformation matrix by passing our identity matrix to the glm :: translate function , along with the shift vector.
Then we multiply our vector by the transformation matrix and print the result. If you still remember how the shift matrix works, then you understand that the resulting vector must be (1 + 1, 0 + 1, 0 + 0) , which is (2, 1, 0) . The code above outputs 210 , which means the shift matrix has done its job.
Let's try to do something more interesting and try to scale, and then rotate the object from the last lesson. At the beginning, we will rotate the container 90 degrees counterclockwise. Then scale it by 0.5 in order to reduce it by 2 times. Let's build a transformation matrix for this.
glm::mat4 trans;
trans = glm::rotate(trans, 90.0f, glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5)); At the beginning, we reduce the container by 0.5, on each axis, and then rotate the container 90 degrees in the Z coordinate. Notice that the texture also rotated. Since we pass the matrix to each of the GLM functions, GLM automatically multiplies the matrices, resulting in a transformation matrix.
Some versions of GLM accept angles in radians rather than degrees. If you have such a version, then convert degrees to radians using glm :: radians (90.0f) .
The next big question is how to transfer the transformation matrix to the shader. We said earlier that GLSL is of type mat4 . So it remains for us to take mat4 as a uniform variable and multiply the position vector by this matrix.
#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 color;
layout (location = 2) in vec2 texCoord;
out vec3 ourColor;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(position, 1.0f);
ourColor = color;
TexCoord = vec2(texCoord.x, 1.0 - texCoord.y);
} GLSL also has mat2 and mat3 types , which provide the same operations as vectors. All operations mentioned in this article are available in matrix types.
We added uniform and multiplied the position vector by the transformation matrix before passing it to gl_Position . Our container should now become 2 times smaller and rotate 90 degrees. But do we still need to pass the transformation matrix into a shader?
GLuint transformLoc = glGetUniformLocation(ourShader.Program, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));At the beginning, we get the uniform position of the variable and then send the matrix data to it using the glUniform function with the Matrix4fv postfix . The first argument must be the position of the variable. The second argument tells OpenGL how many matrices we are going to send, in our case 1. The third argument says whether the matrix should be transposed. OpenGL developers often use an internal matrix format called column-major ordering, which is used by GLM by default, so we don’t need to transpose matrices, we can leave GL_FALSE . The last parameter is, in fact, the data, but GLM does not store the data exactly as OpenGL wants to see it, so we convert it using value_ptr .
We created a transformation matrix, declared uniform in the vertex shader, and sent the matrix in the shader with which we correct the vertex coordinates. The result should be something like this:
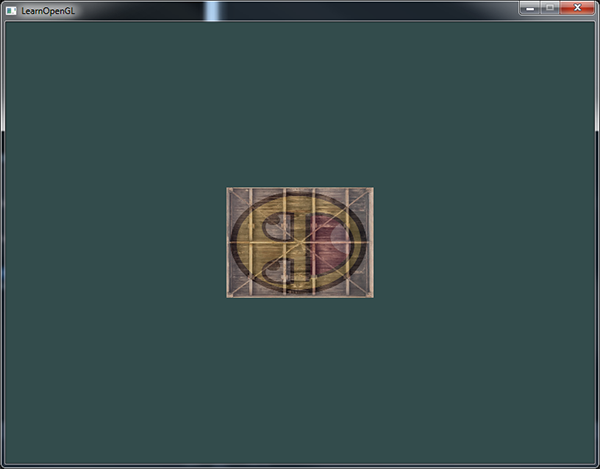
Excellent! Our container really turned left and became 2 times smaller, so the transformation was successful. Now, let's make our container rotate in real time, and also move it to the lower right corner. In order to do this, you will have to perform calculations at each iteration of the main loop. We use the GLFW function to get the time to change the angle with time:
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans,(GLfloat)glfwGetTime() * 50.0f, glm::vec3(0.0f, 0.0f, 1.0f));Keep in mind that before we could declare a transformation matrix anywhere, but now we create it at each iteration so that we can update the rotation for each frame. This means that we must recreate the transformation matrix at each iteration of the game cycle. Usually, when there are several objects on the scene, their transformation matrices are recreated with new values at each iteration of the rendering.
Now we rotate the object around the center (0, 0, 0) , and after that we shift the rotated version to the lower-right corner of the screen. Remember that the real sequence of applying transformations is read in the reverse order: even in the code, we shift at the beginning and then rotate, then the transformations are applied in the reverse order, at the beginning, turn, then shift. Understanding all these transformations and how they affect objects is rather difficult. Try to experiment with transformations and you will quickly get used to them.
If you did everything correctly, then you will get something like this:
That's all. A shifted container that rotates over time, and all this is done with a single transformation matrix! Now you can see why the matrices are so strong in the graphics world. We can define an unlimited number of transformations and combine them into one matrix for subsequent reuse. Using such transformations in the vertex shader allows us not to change the vertex data, which saves us processor time, since we do not need to send data to the buffer.
If you weren’t able to get the correct result or you’re stuck somewhere, then take a look at the source code along with the vertex and fragment shaders.
In the next lesson, we will discuss how to use matrices to define different coordinate spaces for our vertices. This will be a new step in the world of 3D graphics in real time!
Exercises
- Change the sequence of actions in the last transformation, see what happens, try to justify why the result is this. Decision
- Try drawing another container by calling glDrawElements , but just place this container elsewhere with a different transformation. Let it be in the upper right corner and instead of rotation - it will change its size (here you can use the sin function): Solution
