Recurrent formulas for calculating iterative summation errors of binary numbers of limited length
In this article, we continue to consider the problem of computer calculations of decimal numbers using binary arithmetic, which was discussed in the previous topic [1]. The article will focus on errors that are commonly referred to in the literature as rounding errors. And, in particular, errors that result from iterative summation of a large number of identical decimal numbers represented in binary form by a limited bit space. As a result of the studies, simple recurrence relations were obtained that allow one to precisely determine the error of computer iterative calculations of partial sums of any number of identical terms at any step of the iteration.
We will consider real positive binary numbers with a fixed number of L significant digits. By a fixed number of L significant digits, we mean L digits, which are counted from left to right, starting from the highest non-zero digit. Missing to L, the number of digits in the number on the right is padded with zeros. So, if the number of significant digits is fixed with the value L = 5, then the number 0.0011 will have the following significant digits: 11000. If we now write our number to a 5-bit computer as a floating-point number, then in the area of the machine mantissa it will be written: .11000 . This number will be presented in the computer in normalized form with an exponent equal to 2 ^ -2.
A floating-point number is written in a machine word as the product of a fractional mantissa by an exponent, the order of which indicates the position of the point in a number represented in natural form. If the number of digits of the mantissa of the number does not coincide with the number L of digits of the machine mantissa, the number is normalized by shifting the mantissa in one direction or another so that the leading nonzero digit of the number is located in the highest bit of the machine mantissa. In this case, the order of the exponent is adjusted for the number of shifts.
Consider the number in natural form. If the number of its significant digits exceeds a certain fixed number of L digits, then it must be converted so that the number of its significant digits becomes equal to L. This is achieved by discarding the extra low digits. When discarding the lower digits, the number can be rounded to L digits, or it simply truncates the extra low digits. So, in the case of truncation, the binary number 10.0011, presented in its natural form, for L = 5, will be written as 10.001. The same number written in exponential normalized form will look like 0.10001 * 2 ^ 2. Here we have two equivalent entries of the same number.
The reduction of a number represented in its natural form to a number with the number of significant digits L will be called optimization. We introduce this concept to distinguish it from the operation of normalizing numbers written in exponential form. From a mathematical point of view, these are two equivalent operations.
Next, we consider the case of truncating the least significant digits in a binary number without rounding. Numbers will be considered presented in their natural form.
Suppose we have a certain number 2 ^ p ≤ Z <2 ^ (p + 1), where p is a signed integer equal to the distance from the leading point to the leading nonzero digit in the number Z, written in natural form. If the leading nonzero digit is located to the left of the point, then p> 0. If the digit is located to the right of the point, then p <0. So, for the number Z = 0.000101 we will have p = -4 and for this case: 2 ^ (- 4) ≤Z <2 ^ (- 3).
Consider a sequence of real binary numbers X 0 , X 1 , ... X i ... lying in the intervals:
2 ^ p ≤ X 0 <2 ^ (1 + p) ≤ X 1 <2 ^ (2 + p); .. .; 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1) ...
For example, for p = -3 we will have 2 ^ p = 2 ^ -3 = 0.001. Our sequence then will look like 0.001 ≤ X 0 <0.01 ≤ X 1 <0.1, ..., 2 ^ (i -3) ≤ X i <2 ^ (i -2) ...
Take some real number 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1), having a limited number of L significant digits. Next, take the sum of k i elementary terms: Z + Z + ... = k i Z, where Z = X 0 , k i ≥ 0 is an integer. We choose k i such that 2 ^ (i + p) ≤ X i + k i Z <2 ^ (i + p +1). In this amount, the maximum number k ielementary terms Z, in which the value of the sum does not exceed the right border of the interval, can be found by the formula k i = ⌊ (2 ^ (i + p + 1) -X i ) / Z⌋, where the brackets ⌊ ⌋ mean rounding to the nearest integer in smaller side.
If now we add one more elementary term Z to X i + k i Z, we obtain X i + 1 = X i + k i Z + Z = X i + Z (k i +1) ≥ 2 ^ (i + p +1 ) The value of the newly received amount will exceed or will be equal to the right boundary value of the interval. Therefore, the number of digits in the number X i + 1 = X i + Z (k i+1) becomes L + 1. In order to fulfill the requirement that the number of significant digits be equal to L, the resulting number must be optimized, i.e. lead to a number in which there will be L significant digits. To do this, it is necessary to discard the lowest digit. The operation of discarding the least significant digit in the number X i will be written as X i ¬1 . For example, if in the number X = 10.0011 we discard one least significant digit, then it will be written as X ¬1 = 10.001 . In the general case, writing X ¬t will mean that t low-order bits are dropped out of X.
After a partial sum X i + 1 = X i + Z (k i+1) превысит значение 2^( i+p +1), которое мы будем называть правым граничным значением, старшая ненулевая цифра суммы окажется смещенной относительно фиксированной точки влево. Общее количество значащих цифр превысит число L на единицу и результат должен быть оптимизирован. Поскольку на i-м шаге итерации в результате оптимизации, в числе Xi младшая цифра отбрасывается, то число становится равным Xi¬1, тогда младшая цифра в слагаемом Z также может быть отброшена, т.к. на дальнейшие вычисления она влиять не будет.
Например. Пусть L=5. Найдем сумму двух чисел X =1.10111 и Z=0.10011. Т.к. количество цифр в X превышает величину L, оно должно быть оптимизировано. После оптимизации получим: X¬1= 1.1011. Add to this number Z = 0.1001 ** 1 **. We get X ¬1 + Z = 1.1011 + 0.1001 ** 1 ** = 10.0100 ** 1 **. Here, the number of digits after the decimal point in the term X ¬1 is less than the number of digits in the term Z. Therefore, the lowest digit in Z, marked in bold, on the one hand, always adds up to zero, and on the other, the result of adding the lower digits in this case is out of range L significant digits and therefore, when truncated, does not affect the total amount. It follows that the sum will not change if it is written as X ¬1 + Z ¬1 = 1.1011 + 0.1001 = 10.0100. Since the number of digits in this sum exceeded the value of L, the resulting number should also be optimized. Discarding the lowest digit, we get an optimized number 10.010 with L = 5 significant digits.
Thus, the values of the partial sums X i and X i + 1 differ by a maximum of k i elementary terms. The number of significant digits of the partial sums lying in the interval [X i , X i + 1 ) is L and therefore their values are calculated without rounding and, accordingly, do not introduce errors. Addition (k i + 1) of the term to a partial sum leads to the excess of the right boundary value or its equality. If the partial sum at some iteration step exceeds the right boundary value or is equal to it, then the number of significant digits in the sum becomes L + 1 and optimization is required. After each excess of the right boundary value, the number of significant digits of the elementary terms Z participating in the formation of new partial sums decreases by one and after the ith right boundary value the elementary term becomes equal to Z ¬i .
X i + 1 = (X i + (k i + 1 + 1 ) Z ¬i ) ¬1 , X 0 = Z, i = 0.1 ...
k i + 1 = ⌊ (2 ^ (p + i) - Xi ) / Z ¬i ⌋ , p is a signed integer.
The iteration step number N i + 1 , at which the partial sum X i + 1 exceeded the right boundary value, can be determined by the recurrence relation:
N i + 1 = (k i + 1 +1) + N i .
Now consider what error we get when iteratively summing up decimal real numbers represented in binary as a result of the truncation operation.
It is known that any decimal number X represented in binary form, after truncating the number of significant digits, can be written as X = B + g, where B is the representation of the decimal number X in binary form with a limited fixed number of significant digits, g is the absolute error representations of the number as a result of truncation. This error can be defined as g = XB, g ≥0. When summing i elementary terms, this error accumulates and becomes equal to ig.
However, this is not the only error that is formed during the recursive addition of identical elementary terms. As a result of rounding or truncation, when recursing the calculation of partial amounts, rounding errors are also generated.
The recurrence relations we derived allow us at any step of the iteration to obtain the exact values of the error in calculating the sum of elementary terms that have the same value.
Consider, for example, partial sums of elementary terms Z = 0.0011101, for which L = 5. For the number Z, we will have p = 0.001. Table 1 shows the results of adding 10 elementary terms for each iteration step.
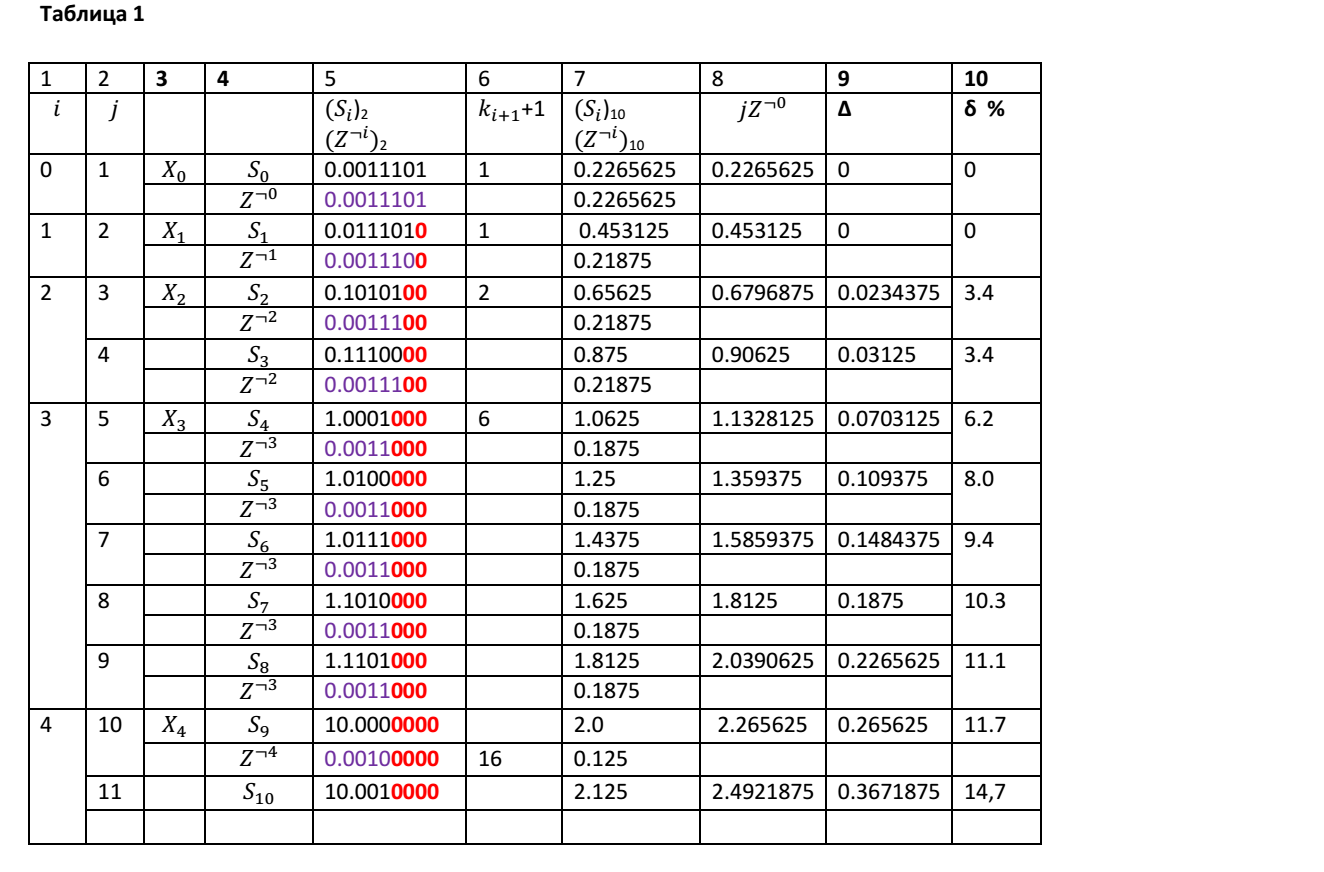
Column 1 of the table shows the numbers i of partial sums X i that have exceeded or become equal to the right boundary of the interval. The second column shows the iteration numbers j. Column 3 shows the notation of partial sums X i for a certain value of i. In column 4 of the table, the designations of the partial sums S j and elementary summands Z ¬i for each iteration step are given, respectively, under each other . Column 5 shows, under each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step. Red letters indicate digits of numbers that do not take part in the formation of partial sums. Column 6 shows the values of the coefficients ki + 1 + 1 , which are used in our recurrence formula to calculate X i + 1 . Column 7 shows, under each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step in decimal form. Column 8 shows the theoretical values of the sums of elementary terms Z provided that rounding errors are not taken into account. Column 9 presents the values of the absolute errors of the calculation at each iteration step, which are calculated by the formula Δ = (S j ) 10 - jZ ¬0 . Column 9 presents the values of the relative errors calculated by the formula: δ = Δ / jZ ¬0 .
As can be seen from the table, even provided that the elementary terms are represented accurately, without representation errors, during the iterative summation, such an error value is formed very quickly that calculations at a certain iteration step become meaningless. The reason for this error lies in the limitations of the machine word, as well as in the normalization procedure, or, in our case, the optimization of the representation of numbers.
Below we give Table 2, which presents the values of partial sums during iterative summation of the decimal number 0.1 in binary form with a fixed number of significant digits for 51 bit mantissa. The table shows the values of partial sums at points of excess of the right boundary values. The numbers in bold in the table are binary. Numbers not shown in bold are numbers that are represented in decimal code. This table shows the values of partial sums X i , the values of the coefficients k i + 1 + 1 to find the next partial sum X i + 1 in accordance with our recurrence relations.
Iteration step number N i + 1on which the next partial sum exceeded the right boundary value can be determined by the recurrence relation: N i + 1 = (k i + 1 +1) + N i .
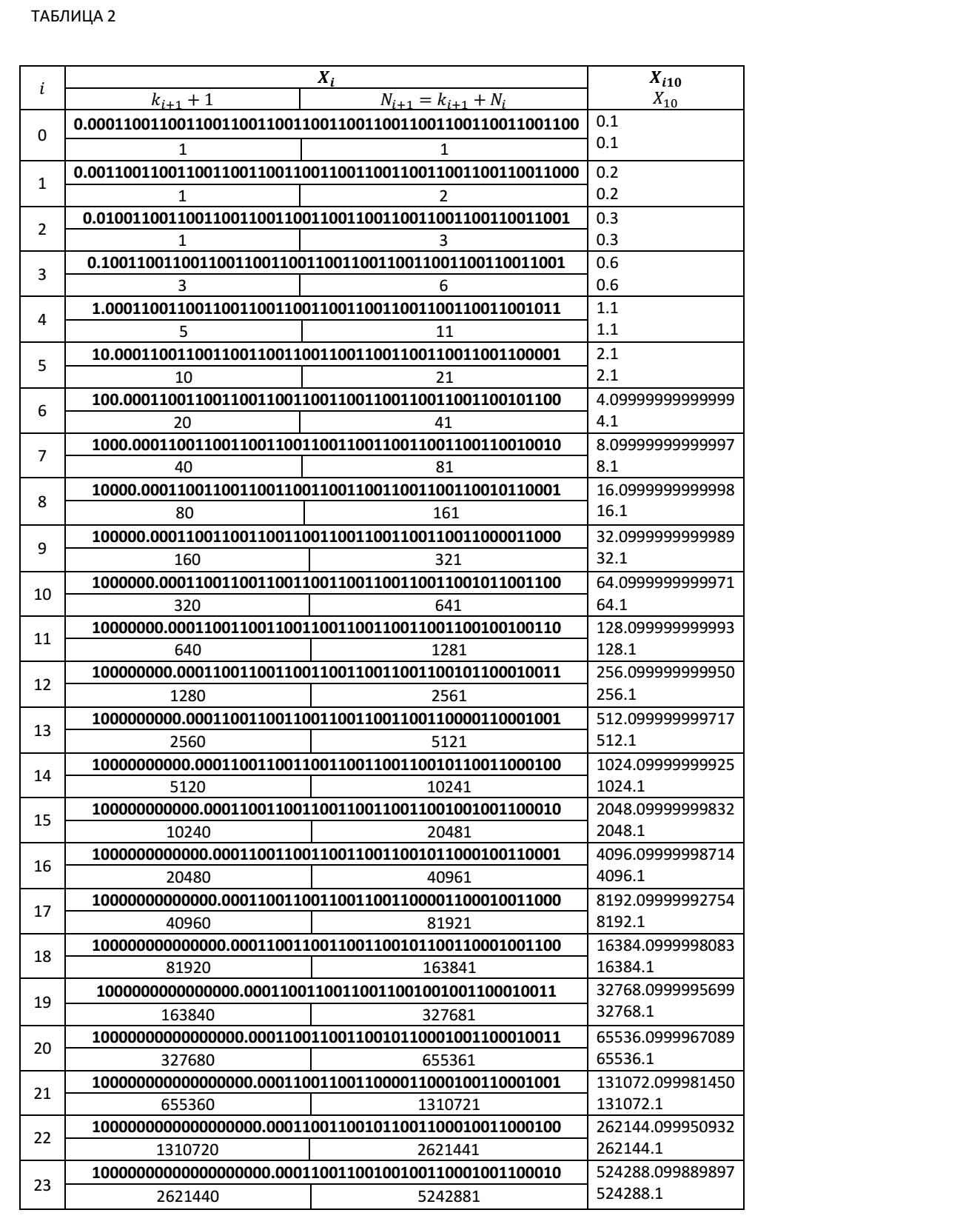
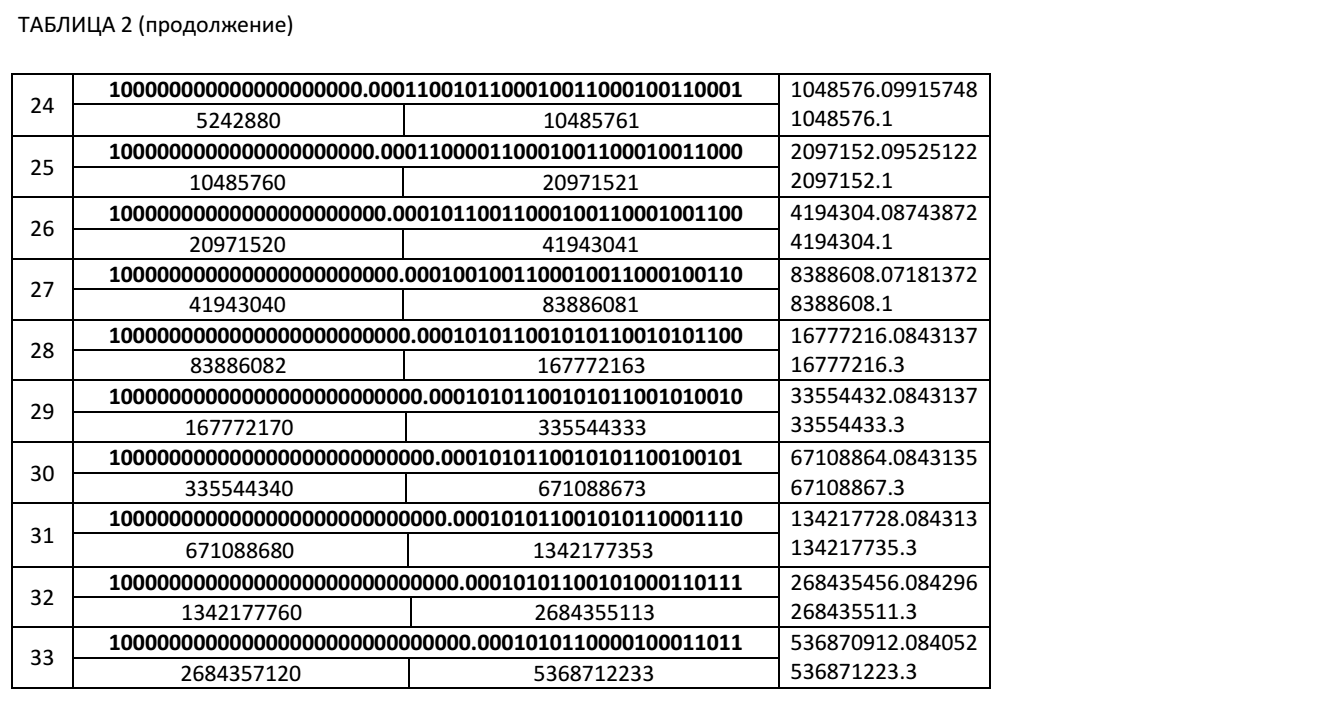
Как видно из Таблицы 2, при числе итераций 5368712233 уже в 6 знаке частичной суммы мы имеем неверную цифру. Абсолютная ошибка вычислений для этого случая составляет Δ= 536871223.3- 536870912.084052=311.215948. А относительная ошибка будет равна δ=311.215948/536871223.3≈0.0000006=0.00006%.
В то же время, если вычислить погрешность представления десятичного числа 0.1 в двоичном виде с 51 значащей цифрой, то мы будем иметь: 0.1=0.0001100110011001100110011001100110011001100110011001100≈ 0.09999999999999997779
Δ=0.1-0.09999999999999997779≈2.221*10^(-17),
δ=2.221*10^(-17)/0.1=2.221*10^(-16)=14*10^(-14)%.
At the iteration step equal to 5368712233, the total absolute error of the representation takes the value 5368712233 * 14 * 10 ^ (- 18) ≈ 0.000000075. The relative error of representation does not change at any step of the iteration.
As we see, the absolute error of the representation is negligible compared to the rounding error during iterative summation.
The recurrence formulas presented here made it possible to obtain accurate calculated rounding errors during the iterative summation of a large number of identical decimal terms represented in binary code.
The author thanks the user mayorovp for the inaccuracies found.
REFERENCES
1. habrahabr.ru/post/309812
We will consider real positive binary numbers with a fixed number of L significant digits. By a fixed number of L significant digits, we mean L digits, which are counted from left to right, starting from the highest non-zero digit. Missing to L, the number of digits in the number on the right is padded with zeros. So, if the number of significant digits is fixed with the value L = 5, then the number 0.0011 will have the following significant digits: 11000. If we now write our number to a 5-bit computer as a floating-point number, then in the area of the machine mantissa it will be written: .11000 . This number will be presented in the computer in normalized form with an exponent equal to 2 ^ -2.
A floating-point number is written in a machine word as the product of a fractional mantissa by an exponent, the order of which indicates the position of the point in a number represented in natural form. If the number of digits of the mantissa of the number does not coincide with the number L of digits of the machine mantissa, the number is normalized by shifting the mantissa in one direction or another so that the leading nonzero digit of the number is located in the highest bit of the machine mantissa. In this case, the order of the exponent is adjusted for the number of shifts.
Consider the number in natural form. If the number of its significant digits exceeds a certain fixed number of L digits, then it must be converted so that the number of its significant digits becomes equal to L. This is achieved by discarding the extra low digits. When discarding the lower digits, the number can be rounded to L digits, or it simply truncates the extra low digits. So, in the case of truncation, the binary number 10.0011, presented in its natural form, for L = 5, will be written as 10.001. The same number written in exponential normalized form will look like 0.10001 * 2 ^ 2. Here we have two equivalent entries of the same number.
The reduction of a number represented in its natural form to a number with the number of significant digits L will be called optimization. We introduce this concept to distinguish it from the operation of normalizing numbers written in exponential form. From a mathematical point of view, these are two equivalent operations.
Next, we consider the case of truncating the least significant digits in a binary number without rounding. Numbers will be considered presented in their natural form.
Suppose we have a certain number 2 ^ p ≤ Z <2 ^ (p + 1), where p is a signed integer equal to the distance from the leading point to the leading nonzero digit in the number Z, written in natural form. If the leading nonzero digit is located to the left of the point, then p> 0. If the digit is located to the right of the point, then p <0. So, for the number Z = 0.000101 we will have p = -4 and for this case: 2 ^ (- 4) ≤Z <2 ^ (- 3).
Consider a sequence of real binary numbers X 0 , X 1 , ... X i ... lying in the intervals:
2 ^ p ≤ X 0 <2 ^ (1 + p) ≤ X 1 <2 ^ (2 + p); .. .; 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1) ...
For example, for p = -3 we will have 2 ^ p = 2 ^ -3 = 0.001. Our sequence then will look like 0.001 ≤ X 0 <0.01 ≤ X 1 <0.1, ..., 2 ^ (i -3) ≤ X i <2 ^ (i -2) ...
Take some real number 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1), having a limited number of L significant digits. Next, take the sum of k i elementary terms: Z + Z + ... = k i Z, where Z = X 0 , k i ≥ 0 is an integer. We choose k i such that 2 ^ (i + p) ≤ X i + k i Z <2 ^ (i + p +1). In this amount, the maximum number k ielementary terms Z, in which the value of the sum does not exceed the right border of the interval, can be found by the formula k i = ⌊ (2 ^ (i + p + 1) -X i ) / Z⌋, where the brackets ⌊ ⌋ mean rounding to the nearest integer in smaller side.
If now we add one more elementary term Z to X i + k i Z, we obtain X i + 1 = X i + k i Z + Z = X i + Z (k i +1) ≥ 2 ^ (i + p +1 ) The value of the newly received amount will exceed or will be equal to the right boundary value of the interval. Therefore, the number of digits in the number X i + 1 = X i + Z (k i+1) becomes L + 1. In order to fulfill the requirement that the number of significant digits be equal to L, the resulting number must be optimized, i.e. lead to a number in which there will be L significant digits. To do this, it is necessary to discard the lowest digit. The operation of discarding the least significant digit in the number X i will be written as X i ¬1 . For example, if in the number X = 10.0011 we discard one least significant digit, then it will be written as X ¬1 = 10.001 . In the general case, writing X ¬t will mean that t low-order bits are dropped out of X.
After a partial sum X i + 1 = X i + Z (k i+1) превысит значение 2^( i+p +1), которое мы будем называть правым граничным значением, старшая ненулевая цифра суммы окажется смещенной относительно фиксированной точки влево. Общее количество значащих цифр превысит число L на единицу и результат должен быть оптимизирован. Поскольку на i-м шаге итерации в результате оптимизации, в числе Xi младшая цифра отбрасывается, то число становится равным Xi¬1, тогда младшая цифра в слагаемом Z также может быть отброшена, т.к. на дальнейшие вычисления она влиять не будет.
Например. Пусть L=5. Найдем сумму двух чисел X =1.10111 и Z=0.10011. Т.к. количество цифр в X превышает величину L, оно должно быть оптимизировано. После оптимизации получим: X¬1= 1.1011. Add to this number Z = 0.1001 ** 1 **. We get X ¬1 + Z = 1.1011 + 0.1001 ** 1 ** = 10.0100 ** 1 **. Here, the number of digits after the decimal point in the term X ¬1 is less than the number of digits in the term Z. Therefore, the lowest digit in Z, marked in bold, on the one hand, always adds up to zero, and on the other, the result of adding the lower digits in this case is out of range L significant digits and therefore, when truncated, does not affect the total amount. It follows that the sum will not change if it is written as X ¬1 + Z ¬1 = 1.1011 + 0.1001 = 10.0100. Since the number of digits in this sum exceeded the value of L, the resulting number should also be optimized. Discarding the lowest digit, we get an optimized number 10.010 with L = 5 significant digits.
Thus, the values of the partial sums X i and X i + 1 differ by a maximum of k i elementary terms. The number of significant digits of the partial sums lying in the interval [X i , X i + 1 ) is L and therefore their values are calculated without rounding and, accordingly, do not introduce errors. Addition (k i + 1) of the term to a partial sum leads to the excess of the right boundary value or its equality. If the partial sum at some iteration step exceeds the right boundary value or is equal to it, then the number of significant digits in the sum becomes L + 1 and optimization is required. After each excess of the right boundary value, the number of significant digits of the elementary terms Z participating in the formation of new partial sums decreases by one and after the ith right boundary value the elementary term becomes equal to Z ¬i .
X i + 1 = (X i + (k i + 1 + 1 ) Z ¬i ) ¬1 , X 0 = Z, i = 0.1 ...
k i + 1 = ⌊ (2 ^ (p + i) - Xi ) / Z ¬i ⌋ , p is a signed integer.
The iteration step number N i + 1 , at which the partial sum X i + 1 exceeded the right boundary value, can be determined by the recurrence relation:
N i + 1 = (k i + 1 +1) + N i .
Now consider what error we get when iteratively summing up decimal real numbers represented in binary as a result of the truncation operation.
It is known that any decimal number X represented in binary form, after truncating the number of significant digits, can be written as X = B + g, where B is the representation of the decimal number X in binary form with a limited fixed number of significant digits, g is the absolute error representations of the number as a result of truncation. This error can be defined as g = XB, g ≥0. When summing i elementary terms, this error accumulates and becomes equal to ig.
However, this is not the only error that is formed during the recursive addition of identical elementary terms. As a result of rounding or truncation, when recursing the calculation of partial amounts, rounding errors are also generated.
The recurrence relations we derived allow us at any step of the iteration to obtain the exact values of the error in calculating the sum of elementary terms that have the same value.
Consider, for example, partial sums of elementary terms Z = 0.0011101, for which L = 5. For the number Z, we will have p = 0.001. Table 1 shows the results of adding 10 elementary terms for each iteration step.

Column 1 of the table shows the numbers i of partial sums X i that have exceeded or become equal to the right boundary of the interval. The second column shows the iteration numbers j. Column 3 shows the notation of partial sums X i for a certain value of i. In column 4 of the table, the designations of the partial sums S j and elementary summands Z ¬i for each iteration step are given, respectively, under each other . Column 5 shows, under each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step. Red letters indicate digits of numbers that do not take part in the formation of partial sums. Column 6 shows the values of the coefficients ki + 1 + 1 , which are used in our recurrence formula to calculate X i + 1 . Column 7 shows, under each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step in decimal form. Column 8 shows the theoretical values of the sums of elementary terms Z provided that rounding errors are not taken into account. Column 9 presents the values of the absolute errors of the calculation at each iteration step, which are calculated by the formula Δ = (S j ) 10 - jZ ¬0 . Column 9 presents the values of the relative errors calculated by the formula: δ = Δ / jZ ¬0 .
As can be seen from the table, even provided that the elementary terms are represented accurately, without representation errors, during the iterative summation, such an error value is formed very quickly that calculations at a certain iteration step become meaningless. The reason for this error lies in the limitations of the machine word, as well as in the normalization procedure, or, in our case, the optimization of the representation of numbers.
Below we give Table 2, which presents the values of partial sums during iterative summation of the decimal number 0.1 in binary form with a fixed number of significant digits for 51 bit mantissa. The table shows the values of partial sums at points of excess of the right boundary values. The numbers in bold in the table are binary. Numbers not shown in bold are numbers that are represented in decimal code. This table shows the values of partial sums X i , the values of the coefficients k i + 1 + 1 to find the next partial sum X i + 1 in accordance with our recurrence relations.
Iteration step number N i + 1on which the next partial sum exceeded the right boundary value can be determined by the recurrence relation: N i + 1 = (k i + 1 +1) + N i .


Как видно из Таблицы 2, при числе итераций 5368712233 уже в 6 знаке частичной суммы мы имеем неверную цифру. Абсолютная ошибка вычислений для этого случая составляет Δ= 536871223.3- 536870912.084052=311.215948. А относительная ошибка будет равна δ=311.215948/536871223.3≈0.0000006=0.00006%.
В то же время, если вычислить погрешность представления десятичного числа 0.1 в двоичном виде с 51 значащей цифрой, то мы будем иметь: 0.1=0.0001100110011001100110011001100110011001100110011001100≈ 0.09999999999999997779
Δ=0.1-0.09999999999999997779≈2.221*10^(-17),
δ=2.221*10^(-17)/0.1=2.221*10^(-16)=14*10^(-14)%.
At the iteration step equal to 5368712233, the total absolute error of the representation takes the value 5368712233 * 14 * 10 ^ (- 18) ≈ 0.000000075. The relative error of representation does not change at any step of the iteration.
As we see, the absolute error of the representation is negligible compared to the rounding error during iterative summation.
The recurrence formulas presented here made it possible to obtain accurate calculated rounding errors during the iterative summation of a large number of identical decimal terms represented in binary code.
The author thanks the user mayorovp for the inaccuracies found.
REFERENCES
1. habrahabr.ru/post/309812
