Laziness is the engine of progress. Task generator. Part 2
- Tutorial
Sometimes I help to carry out mathematical analysis at the first courses and they need to select tasks on which you can fill your hand. Yes, you can take tasks from the book. But what if you do not find the necessary tasks in the books that are at hand?
How to make your own generator of simple tasks for finding limits / derivatives / integrals will be discussed after the kat.
Ps The experience of creating a similar program is described in the previous part.
As you can see from the picture, we will generate tasks in pdf using LaTex. There have already been many different articles about him , so I will omit the introductory part. We will implement and create tasks through Pascal (but I will describe and hide the general algorithm and hide all the code in spoilers).
First you need to define the concept of a polynomial (polynomial), since trigonometric functions are based precisely on the polynomial. As part of standard operations, you must enter:
Following the usual polynomial, you will need to introduce a polynomial with roots (so that you can search for roots or reduce fractions).
But there will be a peculiarity, since it is necessary to make the same properties not only for the same class, but also for the ordinary polynomial.
And then, following a similar example, we work with trigonometric functions (including the logarithm and e ^ x).
I will make a reservation in advance that I will not use any trigonometric formulas further. This will increase the complexity not only for solving, but also for mapping out tasks.
To simplify working with TeX, a separate class was created, so that later everything could be put into a separate module.
The class is responsible for:
I will make a reservation in advance that the derivative and integral problems are inverse, so only one scheme for two problems is needed.
At the beginning of the course of mathematical analysis, the limits (with x-> inf) most often pop up: inf / inf, 0/0, inf-inf, a / inf and a / b.
This means that the schemes of such tasks should check forlice understanding of the difference.
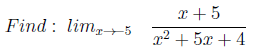
The task is constructed according to the type P1 (x) / P2 (x) * as x tends to the root P1 (x) (and is not the root of P2 (x)).
* P1 (x) and P2 (x) are polynomials with roots from 1 to 3 (sometimes 4th) degrees (random generation)
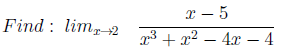
Simple enough. By analogy with the first example, here is zero in the denominator.
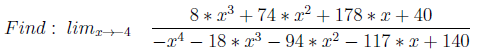
Two polynomials with roots are constructed so that both P (x) have one root. Then, as x tends to this root, the ratio 0/0 will be. Hence the need to differentiate P1 (x) and P2 (x) in order to find the correct answer.
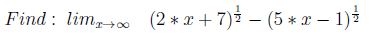
I decided to demonstrate an example by the principles of inf-inf using the example of roots (it was often found in books, but there are other examples).
Here, the basis is that P3 (x) * and P4 (x) * are of the same degree, and the solution is to multiply and divide by the conjugate.
* P3 (x), P4 (x) - polynomials under the root of the first degree

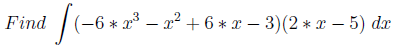
The examples are constructed as follows: the derivative of the function is taken (polynomial / trigonometric function) and you need to find its integral (in fact, the originally taken function).
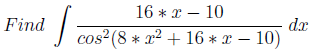
The task can be built in various ways. One of them takes the trigonometric function T (P (x)) (P (x) is a polynomial of the second or higher degree) and multiply T (P (x)) by the derivative P (x). One must be able to notice such a technique in order not to use the expansion of the integral.
There is a wide variety of typical techniques and examples, but for a minimal assessment of understanding the material, such a set helped me out a couple of times. Of course, this set can be expanded and expanded, but this is everyone’s business.
Link to the program: GitHub
In that project, there are other tasks that are not described in this article because of their ambiguous work (tested and updated).
How to make your own generator of simple tasks for finding limits / derivatives / integrals will be discussed after the kat.
Ps The experience of creating a similar program is described in the previous part.
As you can see from the picture, we will generate tasks in pdf using LaTex. There have already been many different articles about him , so I will omit the introductory part. We will implement and create tasks through Pascal (but I will describe and hide the general algorithm and hide all the code in spoilers).
Let's get started
First you need to define the concept of a polynomial (polynomial), since trigonometric functions are based precisely on the polynomial. As part of standard operations, you must enter:
- Polynomial addition
- Subtraction of polynomials
- Multiplication of polynomials
- Graduation
- Text Translation
- Derivative
- Integral
Polynomial class
type polynomial = record
st: integer; // polynomial degree
kof: array of real; // coefficients for x ^ i
function into (x: real): real;
class function operator + (a, b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] + b.kof [i];
end;
rez.st:=stn;
result: = rez;
end;
class function operator- (a, b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (a, b: polynomial): polynomial;
var i, j, stn: integer;
rez: polynomial;
begin
stn: = a.st + b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to a.st do
for j: = 0 to b.st do
begin
rez.kof [i + j]: = rez.kof [i + j] + a.kof [i] * b.kof [j];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (a: integer; b: polynomial): polynomial;
var i: integer;
begin
for i: = 0 to b.st do
b.kof [i]: = a * b.kof [i];
result: = b;
end;
class function operator in (a: polynomial; n: integer): polynomial;
var i: integer;
rez: polynomial;
begin
rez.st:=0;
setlength (rez.kof, 1);
rez.kof [0]: = 1;
for i: = 1 to n do
rez: = rez * a;
result: = rez;
end;
procedure nw (x: integer);
function pltostr: string; // into a string variable
procedure derivative; // derivative
procedure integral; // integral
end;
procedure polynomial.nw (x: integer);
var
i: integer;
begin
st: = x;
setlength (kof, st + 1);
for i: = 0 to st do
kof [i]: = random (-10,10);
while (kof [st] = 0) do
kof [st]: = random (-10,10);
end;
procedure polynomial.integral;
var
i: integer;
begin
setlength (kof, st + 2);
for i: = st downto 1 do
kof [i + 1]: = kof [i] / i;
kof [0]: = 0;
st: = st + 1;
setlength (kof, st + 1);
end;
procedure polynomial.derivative;
var
i: integer;
begin
for i: = 1 to st do
kof [i-1]: = kof [i] * i;
st: = st-1;
setlength (kof, st + 1);
end;
st: integer; // polynomial degree
kof: array of real; // coefficients for x ^ i
function into (x: real): real;
class function operator + (a, b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] + b.kof [i];
end;
rez.st:=stn;
result: = rez;
end;
class function operator- (a, b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (a, b: polynomial): polynomial;
var i, j, stn: integer;
rez: polynomial;
begin
stn: = a.st + b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to a.st do
for j: = 0 to b.st do
begin
rez.kof [i + j]: = rez.kof [i + j] + a.kof [i] * b.kof [j];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (a: integer; b: polynomial): polynomial;
var i: integer;
begin
for i: = 0 to b.st do
b.kof [i]: = a * b.kof [i];
result: = b;
end;
class function operator in (a: polynomial; n: integer): polynomial;
var i: integer;
rez: polynomial;
begin
rez.st:=0;
setlength (rez.kof, 1);
rez.kof [0]: = 1;
for i: = 1 to n do
rez: = rez * a;
result: = rez;
end;
procedure nw (x: integer);
function pltostr: string; // into a string variable
procedure derivative; // derivative
procedure integral; // integral
end;
procedure polynomial.nw (x: integer);
var
i: integer;
begin
st: = x;
setlength (kof, st + 1);
for i: = 0 to st do
kof [i]: = random (-10,10);
while (kof [st] = 0) do
kof [st]: = random (-10,10);
end;
procedure polynomial.integral;
var
i: integer;
begin
setlength (kof, st + 2);
for i: = st downto 1 do
kof [i + 1]: = kof [i] / i;
kof [0]: = 0;
st: = st + 1;
setlength (kof, st + 1);
end;
procedure polynomial.derivative;
var
i: integer;
begin
for i: = 1 to st do
kof [i-1]: = kof [i] * i;
st: = st-1;
setlength (kof, st + 1);
end;
Following the usual polynomial, you will need to introduce a polynomial with roots (so that you can search for roots or reduce fractions).
But there will be a peculiarity, since it is necessary to make the same properties not only for the same class, but also for the ordinary polynomial.
Polynomial with roots
type polynomialwithroot = record
st: integer; // degree of the polynomial
root: array of integer; // roots of the polynomial
kof: array of integer; // coefficients for x ^ i
class function operator + (a, b: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] + b.kof [i];
end;
rez.st:=stn;
result: = rez;
end;
class function operator + (a: polynomialwithroot; b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] + b.kof [i];
end;
rez.st:=stn;
result: = rez;
end;
class function operator + (b: polynomial; a: polynomialwithroot): polynomial;
// var i: integer;
// rez: polynomial;
begin
result: = a + b;
end;
class function operator- (a, b: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator- (a: polynomialwithroot; b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator- (b: polynomial; a: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (a, b: polynomialwithroot): polynomialwithroot;
var i, j, stn: integer;
rez: polynomialwithroot;
begin
stn: = a.st + b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to a.st do
for j: = 0 to b.st do
begin
rez.kof [i + j]: = rez.kof [i + j] + a.kof [i] * b.kof [j];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
setlength (rez.root, rez.st);
for i: = 0 to a.st-1 do
rez.root [i]: = a.root [i];
for i: = 0 to b.st-1 do
rez.root [a.st + i]: = b.root [i];
result: = rez;
end;
class function operator * (a: polynomialwithroot; b: polynomial): polynomial;
var i, j, stn: integer;
rez: polynomial;
begin
stn: = a.st + b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to a.st do
for j: = 0 to b.st do
begin
rez.kof [i + j]: = rez.kof [i + j] + a.kof [i] * b.kof [j];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (b: polynomial; a: polynomialwithroot): polynomial;
// var i, j, stn: integer;
// rez: polynomial;
begin
result: = a * b;
end;
class function operator in (a: polynomialwithroot; n: integer): polynomialwithroot;
var i: integer;
rez: polynomialwithroot;
begin
rez: = a;
for i: = 2 to n do
rez: = rez * a;
result: = rez;
end;
procedure nw;
procedure roots (x: integer);
function pltostr: string;
end;
procedure polynomialwithroot.roots (x: integer);
var i: integer;
begin
st: = x;
setlength (root, st);
for i: = 0 to st-1 do
begin
root [i]: = random (-5,5);
end;
nw;
end;
procedure polynomialwithroot.nw;
var
i, j, sum: integer;
tk: array of integer;
dop: integer;
begin
setlength (kof, st + 1);
setlength (tk, st + 1);
for i: = 0 to st-1 do
kof [i]: = 0;
for i: = 0 to st-1 do
begin
for j: = 0 to st do
tk [j]: = 0;
while (tk [st] = 0) do
begin
sum: = 0;
for j: = 0 to st-1 do
sum: = sum + tk [j];
if (sum = (i + 1)) then
begin
dop: = 1;
for j: = 0 to st-1 do
if (tk [j] = 1) then
dop: = dop * root [j];
for j: = 0 to i do
dop: = - dop;
kof [st-i-1]: = kof [st-i-1] + dop;
end;
tk [0]: = tk [0] +1;
for j: = 0 to st-1 do
begin
tk [j + 1]: = tk [j + 1] + (tk [j] div 2);
tk [j]: = tk [j] mod 2;
end;
end;
end;
kof [st]: = 1;
end;
st: integer; // degree of the polynomial
root: array of integer; // roots of the polynomial
kof: array of integer; // coefficients for x ^ i
class function operator + (a, b: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] + b.kof [i];
end;
rez.st:=stn;
result: = rez;
end;
class function operator + (a: polynomialwithroot; b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] + b.kof [i];
end;
rez.st:=stn;
result: = rez;
end;
class function operator + (b: polynomial; a: polynomialwithroot): polynomial;
// var i: integer;
// rez: polynomial;
begin
result: = a + b;
end;
class function operator- (a, b: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator- (a: polynomialwithroot; b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator- (b: polynomial; a: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st> b.st) then stn: = a.st
else stn: = b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to stn do
begin
if (i <= a.st) then
rez.kof [i]: = rez.kof [i] + a.kof [i];
if (i <= b.st) then
rez.kof [i]: = rez.kof [i] -b.kof [i];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (a, b: polynomialwithroot): polynomialwithroot;
var i, j, stn: integer;
rez: polynomialwithroot;
begin
stn: = a.st + b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to a.st do
for j: = 0 to b.st do
begin
rez.kof [i + j]: = rez.kof [i + j] + a.kof [i] * b.kof [j];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
setlength (rez.root, rez.st);
for i: = 0 to a.st-1 do
rez.root [i]: = a.root [i];
for i: = 0 to b.st-1 do
rez.root [a.st + i]: = b.root [i];
result: = rez;
end;
class function operator * (a: polynomialwithroot; b: polynomial): polynomial;
var i, j, stn: integer;
rez: polynomial;
begin
stn: = a.st + b.st;
setlength (rez.kof, stn + 1);
for i: = 0 to stn do
rez.kof [i]: = 0;
for i: = 0 to a.st do
for j: = 0 to b.st do
begin
rez.kof [i + j]: = rez.kof [i + j] + a.kof [i] * b.kof [j];
end;
while (rez.kof [stn] = 0) do
begin
setlength (rez.kof, stn);
stn: = stn-1;
end;
rez.st:=stn;
result: = rez;
end;
class function operator * (b: polynomial; a: polynomialwithroot): polynomial;
// var i, j, stn: integer;
// rez: polynomial;
begin
result: = a * b;
end;
class function operator in (a: polynomialwithroot; n: integer): polynomialwithroot;
var i: integer;
rez: polynomialwithroot;
begin
rez: = a;
for i: = 2 to n do
rez: = rez * a;
result: = rez;
end;
procedure nw;
procedure roots (x: integer);
function pltostr: string;
end;
procedure polynomialwithroot.roots (x: integer);
var i: integer;
begin
st: = x;
setlength (root, st);
for i: = 0 to st-1 do
begin
root [i]: = random (-5,5);
end;
nw;
end;
procedure polynomialwithroot.nw;
var
i, j, sum: integer;
tk: array of integer;
dop: integer;
begin
setlength (kof, st + 1);
setlength (tk, st + 1);
for i: = 0 to st-1 do
kof [i]: = 0;
for i: = 0 to st-1 do
begin
for j: = 0 to st do
tk [j]: = 0;
while (tk [st] = 0) do
begin
sum: = 0;
for j: = 0 to st-1 do
sum: = sum + tk [j];
if (sum = (i + 1)) then
begin
dop: = 1;
for j: = 0 to st-1 do
if (tk [j] = 1) then
dop: = dop * root [j];
for j: = 0 to i do
dop: = - dop;
kof [st-i-1]: = kof [st-i-1] + dop;
end;
tk [0]: = tk [0] +1;
for j: = 0 to st-1 do
begin
tk [j + 1]: = tk [j + 1] + (tk [j] div 2);
tk [j]: = tk [j] mod 2;
end;
end;
end;
kof [st]: = 1;
end;
And then, following a similar example, we work with trigonometric functions (including the logarithm and e ^ x).
Trigonometric functions
type sinx = record
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type cosx = record
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type tgx = record
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type ctgx = record
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type lnx = record
s: string;
x: polynomial;
procedure nw;
procedure derivative;
end;
type ex = record
s: string;
f, x: polynomial;
procedure nw;
procedure derivative;
end;
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type cosx = record
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type tgx = record
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type ctgx = record
x: polynomial;
s: string;
procedure nw;
procedure derivative; // derivative
end;
type lnx = record
s: string;
x: polynomial;
procedure nw;
procedure derivative;
end;
type ex = record
s: string;
f, x: polynomial;
procedure nw;
procedure derivative;
end;
I will make a reservation in advance that I will not use any trigonometric formulas further. This will increase the complexity not only for solving, but also for mapping out tasks.
A bit about TeX
To simplify working with TeX, a separate class was created, so that later everything could be put into a separate module.
The class is responsible for:
- Creating a new tex file (creation and intro block)
- Add text line by line (at the end of the line there will be a transition to a new line)
- Create a new tex file
- Closing a tex file (closing block and stopping the file)
- Creating pdf via Tex installed on the computer
- Opening pdf file
Module code
type tex = record
namefl: string;
procedure newtex (s: string);
procedure add (s: string);
procedure closetex;
procedure createpdf;
procedure openpdf;
end;
implementation
procedure tex.newtex (s: string);
var
t: text;
begin
namefl: = s;
assign (t, s + '. tex');
rewrite (t);
writeln (t, '\ documentclass [12pt] {article}');
writeln (t, '\ usepackage {amsmath}');
writeln (t, '% \ usepackage [rus] {babel}');
writeln (t, '% \ usepackage [cp1251] {inputenc}');
writeln (t, '\ begin {document}');
close (t);
end;
procedure tex.add (s: string);
var
t: text;
begin
assign (t, namefl + '. tex');
append (t);
writeln (t, '\ [');
writeln (t, s);
writeln (t, '\]');
close (t);
end;
procedure tex.closetex;
var
t: text;
begin
assign (t, namefl + '. tex');
append (t);
writeln (t, '\ end {document}');
close (t);
end;
procedure tex.createpdf;
var
p: System.Diagnostics.Process;
begin
p: = new System.Diagnostics.Process ();
p.StartInfo.FileName: = 'pdflatex';
p.StartInfo.Arguments: = namefl + '. tex';
p.Start ();
end;
procedure tex.openpdf;
p: System.Diagnostics.Process;
begin
p: = new System.Diagnostics.Process ();
p.StartInfo.FileName: = namefl + '. pdf';
p.Start ();
end;
namefl: string;
procedure newtex (s: string);
procedure add (s: string);
procedure closetex;
procedure createpdf;
procedure openpdf;
end;
implementation
procedure tex.newtex (s: string);
var
t: text;
begin
namefl: = s;
assign (t, s + '. tex');
rewrite (t);
writeln (t, '\ documentclass [12pt] {article}');
writeln (t, '\ usepackage {amsmath}');
writeln (t, '% \ usepackage [rus] {babel}');
writeln (t, '% \ usepackage [cp1251] {inputenc}');
writeln (t, '\ begin {document}');
close (t);
end;
procedure tex.add (s: string);
var
t: text;
begin
assign (t, namefl + '. tex');
append (t);
writeln (t, '\ [');
writeln (t, s);
writeln (t, '\]');
close (t);
end;
procedure tex.closetex;
var
t: text;
begin
assign (t, namefl + '. tex');
append (t);
writeln (t, '\ end {document}');
close (t);
end;
procedure tex.createpdf;
var
p: System.Diagnostics.Process;
begin
p: = new System.Diagnostics.Process ();
p.StartInfo.FileName: = 'pdflatex';
p.StartInfo.Arguments: = namefl + '. tex';
p.Start ();
end;
procedure tex.openpdf;
p: System.Diagnostics.Process;
begin
p: = new System.Diagnostics.Process ();
p.StartInfo.FileName: = namefl + '. pdf';
p.Start ();
end;
Task outline
I will make a reservation in advance that the derivative and integral problems are inverse, so only one scheme for two problems is needed.
Limits
At the beginning of the course of mathematical analysis, the limits (with x-> inf) most often pop up: inf / inf, 0/0, inf-inf, a / inf and a / b.
This means that the schemes of such tasks should check for
1. An example where the answer is zero
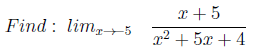
The task is constructed according to the type P1 (x) / P2 (x) * as x tends to the root P1 (x) (and is not the root of P2 (x)).
* P1 (x) and P2 (x) are polynomials with roots from 1 to 3 (sometimes 4th) degrees (random generation)
2. Zero in the denominator
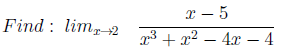
Simple enough. By analogy with the first example, here is zero in the denominator.
3. Zeros in the numerator and denominator
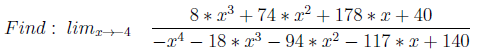
Two polynomials with roots are constructed so that both P (x) have one root. Then, as x tends to this root, the ratio 0/0 will be. Hence the need to differentiate P1 (x) and P2 (x) in order to find the correct answer.
4. Infinity minus infinity
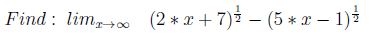
I decided to demonstrate an example by the principles of inf-inf using the example of roots (it was often found in books, but there are other examples).
Here, the basis is that P3 (x) * and P4 (x) * are of the same degree, and the solution is to multiply and divide by the conjugate.
* P3 (x), P4 (x) - polynomials under the root of the first degree
Derivatives and Integrals
“Take and Count”

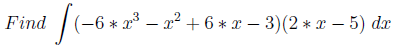
The examples are constructed as follows: the derivative of the function is taken (polynomial / trigonometric function) and you need to find its integral (in fact, the originally taken function).
Cunning method
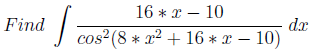
The task can be built in various ways. One of them takes the trigonometric function T (P (x)) (P (x) is a polynomial of the second or higher degree) and multiply T (P (x)) by the derivative P (x). One must be able to notice such a technique in order not to use the expansion of the integral.
Task generation code
unit taskMath;
interface
uses mathUnit;
type taskderivative=record
task:string;
answer:string;
end;
type tasklimits=record
task:string;
answer:string;
end;
function taskintegral1(var s:string):string;
function tasklimits1(var s:string):string;
function tasklimits2(var s:string):string;
function tasklimits3(var s:string):string;
function tasklimits4(var s:string):string;
function taskderivative1(var s:string):string;
function taskderivative2(var s:string):string;
procedure rand(var x:taskderivative);
procedure rand(var x:tasklimits);
implementation
function correct(s:string):string;
var i:integer;
begin
for i:=1 to length(s) do
case s[i] of
'{':s[i]:='(';
'}':s[i]:=')';
end;
result:=s;
end;
function tasklimits1(var s:string):string;
var
p1,p2:polynomialwithroot;
i:integer;
x:integer;
rez:string;
k1,k2,r1,r2:integer;
begin
randomize;
p1.roots(random(1,3));
p2.roots(random(1,3));
i:=random(p1.st)-1;
for i:=i downto 0 do
p2.root[random(p2.st)]:=p1.root[random(p1.st)];
i:=random(p1.st)+random(p2.st);
if(i>p1.st-1)then
begin
x:=p2.root[i-(p1.st-1)];
end
else
x:=p1.root[i];
p1.nw;
p2.nw;
rez:='Find:\;lim_{x\to\!'+inttostr(x)+'}\quad \frac{'+p1.pltostr+'}{'+p2.pltostr+'}';
k1:=0;
k2:=0;
r1:=1;
r2:=1;
s:='При\; сокращении\;(x-'+inttostr(x)+')\; получается\;';
for i:=0 to p1.st-1 do
if(p1.kof[i]=x)then
inc(k1)
else
r1:=r1*(x-p1.kof[i]);
for i:=0 to p2.st-1 do
if(p2.kof[i]=x)then
inc(k2)
else
r2:=r2*(x-p2.kof[i]);
if(k1>k2)then
s:='0';// s:=s+'нуль';
if(k2>k1)then
s:='inf';//s:=s+'нуль\; в\; знаменателе\; и\; получается\; бесконечность';
if(k1=k2)then
s:=inttostr(r1)+'/'+inttostr(r2);//s:=s+'число\;'+floattostr(r1/r2);
s:=correct(s);
result:=rez;
end;
function tasklimits2(var s:string):string;
var
f:polynomialwithroot;
g,x:polynomial;
st:integer;
rez,answ:string;
begin
f.roots(random(1,2));
g.nw(random(1,2));
x.nw(random(1,2));
st:=f.root[random(0,f.st-1)];
rez:='Find:\;lim_{x\to\!'+inttostr(st)+'}\quad \frac{'+(f*g).pltostr+'}{'+(f*x).pltostr+'}';
s:=floattostr(g.into(st))+'/'+floattostr(x.into(st));
s:=correct(s);
result:=rez;
end;
function tasklimits3(var s:string):string;
var
f,g:sqrnpolynomial;
x:polynomial;
rez,answ:string;
begin
f.nw(random(1,4),2);
g.nw(f.x.st,2);
x:=f.x-g.x;
rez:='Find:\;lim_{x\to\infty}\quad '+f.s+'-'+g.s;
if(x.st+1=f.x.st)then
s:=floattostr(x.kof[x.st])+'/'+floattostr(g.x.kof[g.x.st]+f.x.kof[g.x.st])
else
s:='0';
s:=correct(s);
result:=rez;
end;
function tasklimits4(var s:string):string;
var
f,g:polynomialwithroot;
kf1,kf2:polynomial;
a,i,j,num:integer;
rez,add:string;
begin
f.roots(random(1,2));
g.roots(random((f.st),3));
num:=random(1,f.st-1);
for i:=0 to num-1 do
g.root[i]:=f.root[i];
g.nw;
// writeln(num);
sleep(1000);
num:=0;
for i:=0 to f.st-1 do
for j:=0 to g.st-1 do
if(f.kof[i]=g.kof[j])then num+=1;
// writeln(num);
// sleep(1000);
kf1.nw(random(1,2));
kf2.nw(0);
a:=random(2,5);
add:='\frac{'+(kf1+kf2).pltostr+'}{'+kf1.pltostr+'}';
for i:=1 to length(s) do
if(add[i]='x')then add[i]:='n';
rez:='Find \; x,\; when: \;lim_{n\to\infty}\quad '+
add+'\frac{('+f.pltostr+')^{n^'+inttostr(a)+'}}{('+g.pltostr+')^{n^'+inttostr(a)+'}}=e^{'+floattostr(kf2.kof[0])+'}';
s:=inttostr(num);
result:=rez;
end;
function taskintegral1(var s:string):string;
var
tr1:sinx;
tr2:cosx;
tr3:tgx;
tr4:ctgx;
f,g:polynomial;
r:integer;
rez:string;
begin
rez:='Find\;\int ';
r:=random(1,5);
case r of
1:begin
tr1.x.nw(random(1,3));
tr1.nw;
s:=tr1.s;
tr1.derivative;
rez:=rez+tr1.s+'\;dx';
end;
2:begin
tr2.x.nw(random(1,3));
tr2.nw;
s:=tr2.s;
tr2.derivative;
rez:=rez+tr2.s+'\;dx';
end;
3:begin
tr3.x.nw(random(1,3));
tr3.nw;
s:=tr3.s;
tr3.derivative;
rez:=rez+tr3.s+'\;dx';
end;
4:begin
tr4.x.nw(random(1,3));
tr4.nw;
s:=tr4.s;
tr4.derivative;
rez:=rez+tr4.s+'\;dx';
end;
5:begin
r:=random(1,2);
f.nw(random(1,3));
rez:=rez+'('+f.pltostr+')';
while(r<>0)do
begin
g.nw(random(1,3));
f:=f*g;
rez:=rez+'('+g.pltostr+')';
r:=r-1;
end;
f.integral;
s:=correct(f.pltostr);
rez:=rez+'\;dx';
end;
end;
s:=correct(s);
result:=rez;
end;
function taskderivative1(var s:string):string;
var
sinx1,sinx2:sinx;
cosx1,cosx2:cosx;
tgx1,tgx2:tgx;
ctgx1,ctgx2:ctgx;
f,g:polynomial;
r:integer;
rez:string;
bg,answ:string;
begin
randomize;
sinx1.x.nw(random(1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw(random(1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw(random(1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw(random(1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random(1,4);
case r of
1:begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2:begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3:begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos('+tgx1.x.pltostr+')^2)';
end;
4:begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find\; \frac{d}{dx}\;('+rez;
rez:=rez+')';
r:=random(1,2);
f.nw(random(1,3));
while(r>0)do
begin
g.nw(random(1,3));
rez:=rez+'(';
rez:=rez+g.pltostr;
rez:=rez+')';
f:=f*g;
r:=r-1;
end;
rez:=rez+')';
answ:='('+answ+')*('+g.pltostr+')+(';
g.derivative;
answ:=answ+bg+')*('+g.pltostr+')';
s:=answ;
s:=correct(s);
result:=rez;
end;
function taskderivative2(var s:string):string;
var
sinx1,sinx2:sinx;
cosx1,cosx2:cosx;
tgx1,tgx2:tgx;
ctgx1,ctgx2:ctgx;
f,g,st:polynomial;
r:integer;
rez:string;
answ,bg:string;
begin
randomize;
sinx1.x.nw(random(1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw(random(1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw(random(1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw(random(1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random(1,4);
case r of
1:begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2:begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3:begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos('+tgx1.x.pltostr+')^2)';
end;
4:begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find\; \frac{d}{dx}\;('+rez;
rez:=rez+')^{';
f.nw(random(1,3));
rez:=rez+f.pltostr+'}';
st:=f;
st.derivative;
answ:='(('+bg+')^{'+f.pltostr+'})*(('+st.pltostr+')*ln('+bg+')+('+f.pltostr+')*('+answ+')/('+bg+')';
s:=answ;
s:=correct(s);
result:=rez;
end;
procedure rand(var x:taskderivative);
var
r:integer;
begin
randomize;
r:=random(1,2);
case r of
1:x.task:=taskderivative1(x.answer);
2:x.task:=taskderivative2(x.answer);
end;
end;
procedure rand(var x:tasklimits);
var
r:integer;
begin
randomize;
r:=random(1,4);
case r of
1:x.task:=tasklimits1(x.answer);
2:x.task:=tasklimits2(x.answer);
3:x.task:=tasklimits3(x.answer);
4:x.task:=tasklimits4(x.answer);
end;
end;
end.
interface
uses mathUnit;
type taskderivative=record
task:string;
answer:string;
end;
type tasklimits=record
task:string;
answer:string;
end;
function taskintegral1(var s:string):string;
function tasklimits1(var s:string):string;
function tasklimits2(var s:string):string;
function tasklimits3(var s:string):string;
function tasklimits4(var s:string):string;
function taskderivative1(var s:string):string;
function taskderivative2(var s:string):string;
procedure rand(var x:taskderivative);
procedure rand(var x:tasklimits);
implementation
function correct(s:string):string;
var i:integer;
begin
for i:=1 to length(s) do
case s[i] of
'{':s[i]:='(';
'}':s[i]:=')';
end;
result:=s;
end;
function tasklimits1(var s:string):string;
var
p1,p2:polynomialwithroot;
i:integer;
x:integer;
rez:string;
k1,k2,r1,r2:integer;
begin
randomize;
p1.roots(random(1,3));
p2.roots(random(1,3));
i:=random(p1.st)-1;
for i:=i downto 0 do
p2.root[random(p2.st)]:=p1.root[random(p1.st)];
i:=random(p1.st)+random(p2.st);
if(i>p1.st-1)then
begin
x:=p2.root[i-(p1.st-1)];
end
else
x:=p1.root[i];
p1.nw;
p2.nw;
rez:='Find:\;lim_{x\to\!'+inttostr(x)+'}\quad \frac{'+p1.pltostr+'}{'+p2.pltostr+'}';
k1:=0;
k2:=0;
r1:=1;
r2:=1;
s:='При\; сокращении\;(x-'+inttostr(x)+')\; получается\;';
for i:=0 to p1.st-1 do
if(p1.kof[i]=x)then
inc(k1)
else
r1:=r1*(x-p1.kof[i]);
for i:=0 to p2.st-1 do
if(p2.kof[i]=x)then
inc(k2)
else
r2:=r2*(x-p2.kof[i]);
if(k1>k2)then
s:='0';// s:=s+'нуль';
if(k2>k1)then
s:='inf';//s:=s+'нуль\; в\; знаменателе\; и\; получается\; бесконечность';
if(k1=k2)then
s:=inttostr(r1)+'/'+inttostr(r2);//s:=s+'число\;'+floattostr(r1/r2);
s:=correct(s);
result:=rez;
end;
function tasklimits2(var s:string):string;
var
f:polynomialwithroot;
g,x:polynomial;
st:integer;
rez,answ:string;
begin
f.roots(random(1,2));
g.nw(random(1,2));
x.nw(random(1,2));
st:=f.root[random(0,f.st-1)];
rez:='Find:\;lim_{x\to\!'+inttostr(st)+'}\quad \frac{'+(f*g).pltostr+'}{'+(f*x).pltostr+'}';
s:=floattostr(g.into(st))+'/'+floattostr(x.into(st));
s:=correct(s);
result:=rez;
end;
function tasklimits3(var s:string):string;
var
f,g:sqrnpolynomial;
x:polynomial;
rez,answ:string;
begin
f.nw(random(1,4),2);
g.nw(f.x.st,2);
x:=f.x-g.x;
rez:='Find:\;lim_{x\to\infty}\quad '+f.s+'-'+g.s;
if(x.st+1=f.x.st)then
s:=floattostr(x.kof[x.st])+'/'+floattostr(g.x.kof[g.x.st]+f.x.kof[g.x.st])
else
s:='0';
s:=correct(s);
result:=rez;
end;
function tasklimits4(var s:string):string;
var
f,g:polynomialwithroot;
kf1,kf2:polynomial;
a,i,j,num:integer;
rez,add:string;
begin
f.roots(random(1,2));
g.roots(random((f.st),3));
num:=random(1,f.st-1);
for i:=0 to num-1 do
g.root[i]:=f.root[i];
g.nw;
// writeln(num);
sleep(1000);
num:=0;
for i:=0 to f.st-1 do
for j:=0 to g.st-1 do
if(f.kof[i]=g.kof[j])then num+=1;
// writeln(num);
// sleep(1000);
kf1.nw(random(1,2));
kf2.nw(0);
a:=random(2,5);
add:='\frac{'+(kf1+kf2).pltostr+'}{'+kf1.pltostr+'}';
for i:=1 to length(s) do
if(add[i]='x')then add[i]:='n';
rez:='Find \; x,\; when: \;lim_{n\to\infty}\quad '+
add+'\frac{('+f.pltostr+')^{n^'+inttostr(a)+'}}{('+g.pltostr+')^{n^'+inttostr(a)+'}}=e^{'+floattostr(kf2.kof[0])+'}';
s:=inttostr(num);
result:=rez;
end;
function taskintegral1(var s:string):string;
var
tr1:sinx;
tr2:cosx;
tr3:tgx;
tr4:ctgx;
f,g:polynomial;
r:integer;
rez:string;
begin
rez:='Find\;\int ';
r:=random(1,5);
case r of
1:begin
tr1.x.nw(random(1,3));
tr1.nw;
s:=tr1.s;
tr1.derivative;
rez:=rez+tr1.s+'\;dx';
end;
2:begin
tr2.x.nw(random(1,3));
tr2.nw;
s:=tr2.s;
tr2.derivative;
rez:=rez+tr2.s+'\;dx';
end;
3:begin
tr3.x.nw(random(1,3));
tr3.nw;
s:=tr3.s;
tr3.derivative;
rez:=rez+tr3.s+'\;dx';
end;
4:begin
tr4.x.nw(random(1,3));
tr4.nw;
s:=tr4.s;
tr4.derivative;
rez:=rez+tr4.s+'\;dx';
end;
5:begin
r:=random(1,2);
f.nw(random(1,3));
rez:=rez+'('+f.pltostr+')';
while(r<>0)do
begin
g.nw(random(1,3));
f:=f*g;
rez:=rez+'('+g.pltostr+')';
r:=r-1;
end;
f.integral;
s:=correct(f.pltostr);
rez:=rez+'\;dx';
end;
end;
s:=correct(s);
result:=rez;
end;
function taskderivative1(var s:string):string;
var
sinx1,sinx2:sinx;
cosx1,cosx2:cosx;
tgx1,tgx2:tgx;
ctgx1,ctgx2:ctgx;
f,g:polynomial;
r:integer;
rez:string;
bg,answ:string;
begin
randomize;
sinx1.x.nw(random(1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw(random(1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw(random(1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw(random(1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random(1,4);
case r of
1:begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2:begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3:begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos('+tgx1.x.pltostr+')^2)';
end;
4:begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find\; \frac{d}{dx}\;('+rez;
rez:=rez+')';
r:=random(1,2);
f.nw(random(1,3));
while(r>0)do
begin
g.nw(random(1,3));
rez:=rez+'(';
rez:=rez+g.pltostr;
rez:=rez+')';
f:=f*g;
r:=r-1;
end;
rez:=rez+')';
answ:='('+answ+')*('+g.pltostr+')+(';
g.derivative;
answ:=answ+bg+')*('+g.pltostr+')';
s:=answ;
s:=correct(s);
result:=rez;
end;
function taskderivative2(var s:string):string;
var
sinx1,sinx2:sinx;
cosx1,cosx2:cosx;
tgx1,tgx2:tgx;
ctgx1,ctgx2:ctgx;
f,g,st:polynomial;
r:integer;
rez:string;
answ,bg:string;
begin
randomize;
sinx1.x.nw(random(1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw(random(1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw(random(1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw(random(1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random(1,4);
case r of
1:begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2:begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3:begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos('+tgx1.x.pltostr+')^2)';
end;
4:begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find\; \frac{d}{dx}\;('+rez;
rez:=rez+')^{';
f.nw(random(1,3));
rez:=rez+f.pltostr+'}';
st:=f;
st.derivative;
answ:='(('+bg+')^{'+f.pltostr+'})*(('+st.pltostr+')*ln('+bg+')+('+f.pltostr+')*('+answ+')/('+bg+')';
s:=answ;
s:=correct(s);
result:=rez;
end;
procedure rand(var x:taskderivative);
var
r:integer;
begin
randomize;
r:=random(1,2);
case r of
1:x.task:=taskderivative1(x.answer);
2:x.task:=taskderivative2(x.answer);
end;
end;
procedure rand(var x:tasklimits);
var
r:integer;
begin
randomize;
r:=random(1,4);
case r of
1:x.task:=tasklimits1(x.answer);
2:x.task:=tasklimits2(x.answer);
3:x.task:=tasklimits3(x.answer);
4:x.task:=tasklimits4(x.answer);
end;
end;
end.
Суммируя
There is a wide variety of typical techniques and examples, but for a minimal assessment of understanding the material, such a set helped me out a couple of times. Of course, this set can be expanded and expanded, but this is everyone’s business.
Link to the program: GitHub
In that project, there are other tasks that are not described in this article because of their ambiguous work (tested and updated).
