Building a Voronoi diagram using the divide and conquer method. Lloyd's relaxation
- Tutorial

Recently, on Habrahabr it published an article , entirely dedicated to the Voronoi diagram. In the article, the author describes in detail the Fortune algorithm used to construct the Voronoi Diagram in O (n * log (n)) . It is worth noting that the description of this algorithm has repeatedly appeared in RuNet, while nothing has been said about other algorithms (with the same asymptotics). This article corrects this misunderstanding , and is also an excellent addition to the previously published material.
Below I will talk about the divide and conquer algorithm of constructing the Voronoi diagram for O (n * log (n)), and also, based on my practical experience, about the really cool stuff in which this applies. In general, divide-and-conquer algorithms are a kind of programming classic (I think every programmer has heard about sorting by this method), they are very parallel and easy to read (unless, of course, you know the main idea of the algorithm).
Description of the 'divide and conquer' algorithm for constructing a Voronoi diagram
The initial set of points is sorted by one of the coordinates (put, x) and is divided into two approximately equal sets. Each of the resulting sets is again divided into two, and this happens until no more than two points remain in each of the sets. It is easy to see that there will be no more than such partitions log (n) . Further, for each set obtained, Voronoi diagrams are constructed, after which, in the reverse division order, these diagrams are combined into one. The resulting Voronoi diagram will be the final result.
For the described algorithm to have complexity of the order of O (n * log (n)) , it is necessary to carry out the process of combining two Voronoi diagrams behind O (N). I note that for a set of two points, the Voronoi diagram will be the middle perpendicular of the segment formed by these two points.
Suppose that all points are sorted by the X coordinate, and the initial set is divided into two, and for each a Voronoi diagram is constructed. Let us combine these sets and their diagrams as follows:
⦁ 1. For each of the subsets, we find a convex hull (note that the construction of a convex hull for each of the sets can be performed with the same 'divide and conquer' : that is, at each step of combining the diagrams Voronoi, we combine the convex hulls of these sets in O (N) ).
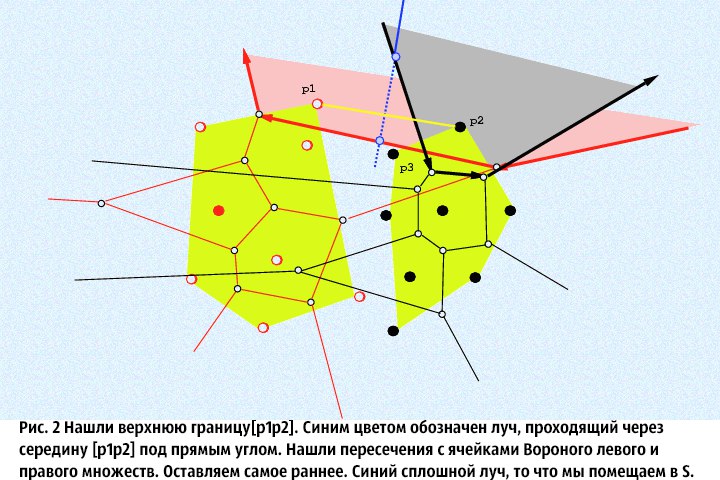
⦁ 2.Now that we have two convex hulls of the original sets, we find the 'upper and lower' boundaries of these sets: that is, we must find two such segments that combine the two given convex hulls into one (naturally, convex). Thus we will fulfill the conditions of step 1, and also get the initializing values for step 3. This step, as I wrote, can be performed in O (N) .
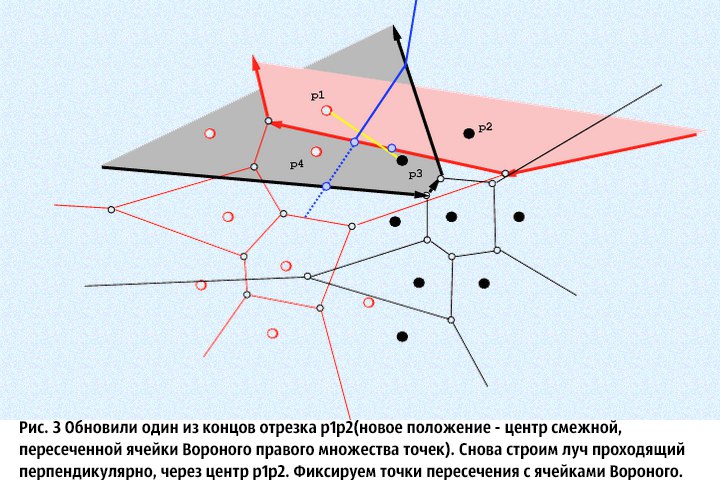
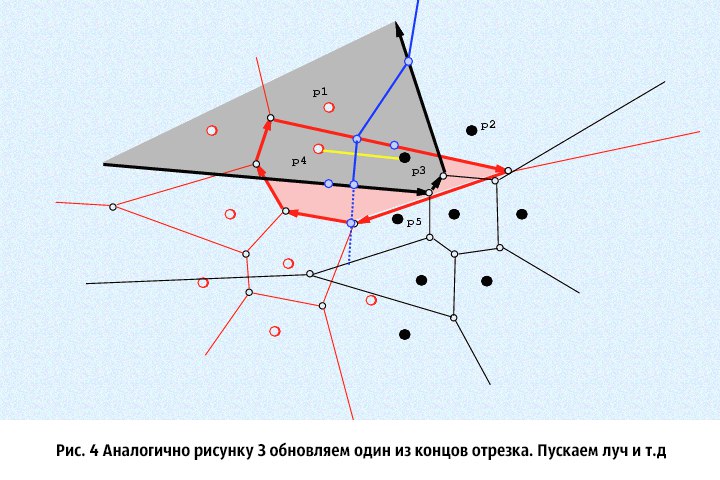
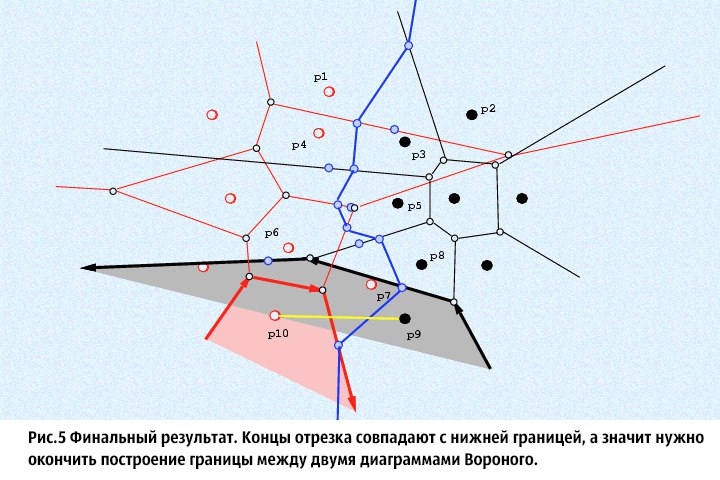
⦁ 3. From the obtained segments in step 2 , we choose any and denote it by L (the remaining one is denoted by Q), and through its middle we perpendicularly launch an endless ray. Imagine that this ray only enters the original set, and find its intersections with the cells of the Voronoi diagrams of the initial sets (it is believed that the ray extends forward, that is, it has a direction). We cross the beam only with those Voronoi cells whose centers are the ends of the segment perpendicular to which we let the beam. We need to find the intersection points of this ray with the corresponding Voronoi cells and choose among them the one that intersects before. We denote this point of M , and the cell which we crossed and let us remember the V . Next, we do the following: that end of the segment L, which is the center for the non-crossed Voronoi cell, we leave it alone, but the one that was the center of the cell we crossed is updated: we crossed one of the sides of the Voronoi cell, then the new end of the segment L will be the center of the Voronoi cell adjacent to this side crossed cell. In the special set S (the boundary of two Voronoi Diagrams is stored in it), it is necessary to add that part of the ray that extends to the intersection with the side of the cell. Repeat step 3 until then, until the value of the endpoints of L , will not be equal to the values of the endpoints of the Q . As a result, in the set Sit turns out to be a continuous broken ray. The proof of many facts presented here (for example, the continuity of a ray in the set S ) can be found in [1] .
⦁ 4. We got a set S, which is a continuous broken ray. This ray is the boundary connecting the Voronoi diagrams of two sets. To get the final result, you need to “wipe” the segments that are to the right of the received ray for the Voronoi diagram of the left set, and to wipe those to the left of the Voronoi diagram of the right set. To do this quickly is not a problem: when we cross a cell with a ray, it is obvious that first the ray will enter it, and then, at some certain moment, it will exit. We need to “catch” these events, and depending on which set of diagrams we are working with (left or right), remove the left or right chain of edges of the Voronoi cell that we crossed by the ray and add the necessary part from the set S there .
The algorithm described above is difficult to understand without a good illustration (the pictures were taken here ):

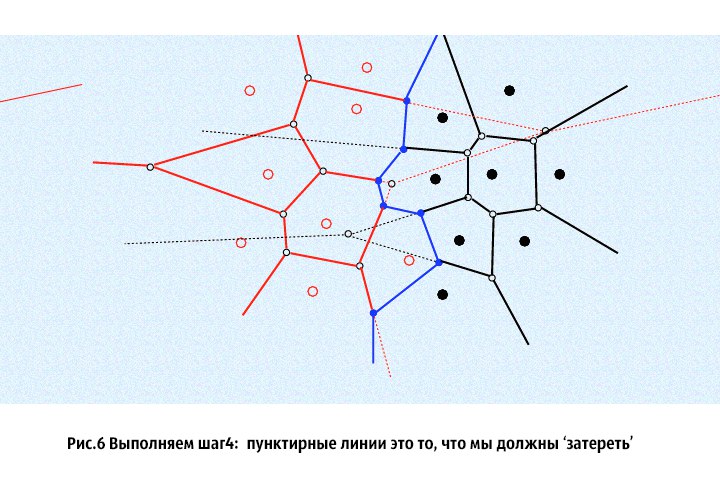
Well, I will end this subsection of the publication on the fact that if the points have the same X coordinate, then it is worth sorting them by the Y coordinate, so that they are divided evenly and consistently.
Voronoi Chart Application - Lloyd's Relaxation
Lloyd's relaxation is one of the amazing and 'sticky' algorithms in which the construction of Voronoi diagrams is actively used. I will describe the algorithm itself:
⦁ 1. We construct the Voronoi diagram for the initial set of points, form the Voronoi cells.
⦁ 2. We find the "Center of Mass" of each Voronoi cell (the sum of the coordinates of the vertices of the Voronoi cell divided by their number).
⦁ 3. We shift the center of each Voronoi cell to the position of the calculated “Center of Mass”.
⦁ 4. Repeat this procedure N times: until the shear distance becomes close to zero.
What do we get in the end? The result can be seen in these two short videos:
It looks beautiful, but a little useless !? Far from it! In my practical experience, Lloyd’s relaxation was used in 3D modeling: in the so-called “mesh remapping”. That is, a grid is given (usually after processing by a cheap Chinese scanner) and the task is to turn the resulting "hash" of triangles into something beautiful and vivid: into what more or less accurate calculations can be made (calculation of the "curvature of the grid", approximation of the points of the triangulation nets with infinitely smooth surfaces, etc.), trying not to deviate very much from the original “scanner” mesh (moreover, this accuracy is set by the user, and this kind of “reming” is called adaptive. There is also uniform “reming” ( uniform) - here, it is not the deviation that is set, but the desired edge length in the triangle). I started talking a little and forgot to explain what we mean by the word 'beautiful' mesh. We call the grid 'beautiful'if in its structure it consists mainly of equilateral triangles, and the valency of each vertex in such a grid is 6 (if the vertex is internal, that is 360. / 6. = 60 deg. - degree of angle of an equilateral triangle) or 4 (if the vertex lies on an open edge, that is, triangles with a given vertex 3). Well, one of the important steps in obtaining such a grid is to build a Voronoi diagram and use Lloyd's relaxation . Actually, we get something in this spirit (neatly, the pictures are big!):
Pictures of the result of the work of 'remeshing', coded by me
Before:

After:

And now before and after in one image:
By the way, you can see that the original was obtained using the Marching Cubes algorithm .

After:

And now before and after in one image:
By the way, you can see that the original was obtained using the Marching Cubes algorithm .
Well, smaller pictures, but from the Internet:
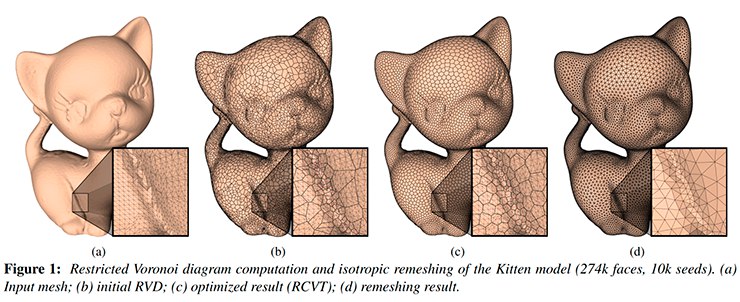
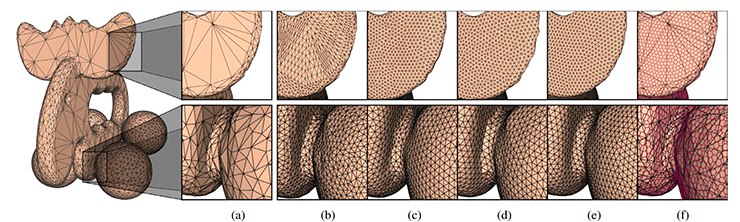
And ... (where would it be without it) - a statue of David:

Beauty, and more!
I would like to conclude that the use of Lloyd's algorithm is expensive. And to obtain a faster result, without much loss in quality, the so-called 'Energy Minimization' methods were developed. You can read in [2]
Useful links and literature
[0] Cool article on Habrahabr about Voronoi diagrams
[1] Original description of the algorithm, with all the proofs
[2] Comparison of the 'Minimize Energy' methods
[3] Small article on the 'Divide and conquer' algorithm for constructing the Voronoi diagram
