Mysterious math genius and writer are promoting the solution of the permutation problem
- Transfer
New evidence for the authorship of Australian science fiction writer Greg Egan and evidence from 2011, anonymously published in the network, have been recognized as significant breakthroughs in the study of the riddle that mathematicians have been studying for 25 years

On September 16, 2011, an anime fan posted a mathematical question 4chan on the forum about the cult TV series Haruni Suzumiya's Melancholy . The first season of the show, where there were time travels, was shown in a manner different from chronological, and during the subsequent show and release on DVD, the order of the episodes was changed again. On the Internet, fans argued about the order in which the series is best to watch, and the author of the question asked if the viewers wanted to watch the series in all possible ways, how many episodes would be on their shortest list? [ referring to a list in which you can find any sequence of episodes / approx. trans. ]
In less than an hour, one anonymous author gave the answer to the question - not a complete solution, but a lower bound for the required number of episodes. From his reasoning, applicable to any number of episodes, it followed that for Haruhi's first season, consisting of 14 episodes, viewers would have to watch at least 93,884,313,611 episodes in a row in order to study all possible permutations. “Examine the evidence for flaws that I might have missed,” the author wrote a reply.
The proof of seven years remained unnoticed in the mathematical community - it turned out that at that moment only one professional mathematician noticed him, and he did not study it carefully enough. But suddenly last month, Australian science fiction writer Greg Egan proved the existence of a newthe upper limit on the required number of episodes. Opening Egan re-raised interest in the problem and drew attention to the record concerning the lower boundary, from 2011. Both of these proofs are now regarded as significant breakthroughs in the study of the riddle that mathematicians have been researching for at least 25 years.
Mathematicians quickly checked the upper bound from Eagan, which, like the lower bound, applies to sequences of any length. Then Robin Houston, a mathematician at Kiln, a data visualization company, and Jay Panton of Marquette University, Milwaukee, independently confirmed the work of an anonymous author with 4chan. “A lot of effort went into verifying the correctness of this hypothesis,” said Panton, since the key ideas of the proof were not clearly expressed.
And now Houston and Panton, together with Vince Vater of the University of Florida, have written a formal work . In it, they indicated the first author as an “anonymous poster 4chan”.
“The strangeness of the situation is that this very elegant proof of a previously unknown fact appeared in such an unlikely place,” said Houston.
Cities permutations
If there are only three episodes in the series, there are six possible ways to watch them: 123, 132, 213, 231, 312, and 321. You can paste them together and make a list of 18 episodes that include each order. However, there is also a more efficient way of gluing: 123121321. Such a sequence containing all permutations of a set of n characters is called super-permutation.
In 1993, Daniel Ashlok and Janet Tilotson found that when studying the shortest super-permutations for different values of n, factorials quickly begin to appear - the same values, written as n !, that is, multiplying all numbers from 1 to n (for example, 4 ! = 4 * 3 * 2 * 1).
If there is only 1 episode in your series, then the length of the shortest super-permutation will be equal to 1! (also known as the good old unit). For a two-episode series, the shortest super-permutation (121) has a length of 2! + 1! .. For three episodes (example above) the length is equal to 3! + 2! + 1 !, and for four episodes (123412314231243121342132413214321) it will be 4! + 3! + 2! + 1! .. The factorial rule became generally accepted (although no one could prove that it was true for all n), and later mathematicians confirmed it for n = 5.
Then in 2014, Houston hit the mathematicians, showingthat for n = 6 the rule stops working. The rule predicts that looking at six episodes in all possible ways would require 873 episodes, but Houston found a way to do it in 872. And since there is an easy way to turn a short super-permutation for n characters into a short super-permutation for n + 1 characters, the Houston example meant that the rule factorials does not work for all n> 6.
Building Houston transforms the super-permutation problem into the famous traveling salesman problem, which is looking for the shortest path through several cities. Specifically, super-permutations are associated with the “asymmetric” task of the traveling salesman, in which each path between the two cities has its price (not necessarily the same in both directions), and the goal is to find the cheapest way through all the cities.
This transformation is easy to understand: imagine that each permutation is a city, and imagine the path from each permutation to each other permutation. In the super-permutation problem, we need the shortest sequence of digits in which all permutations are present, so our goal is to go through all permutations so as to add as few numbers as possible to the initial permutation. We declare that the cost of each path is simply equal to the number of digits we need to attach to the end of the first permutation in order to get the second one. In the example with n = 3, the path from 231 to 312 costs $ 1, since we only need to add 2 to the end of 231 to get 312, and the path from 231 to 132 cost $ 2, because we need to add 32. In such a formulation, the cheapest way is through all cities directly correspond to the shortest super-permutation.
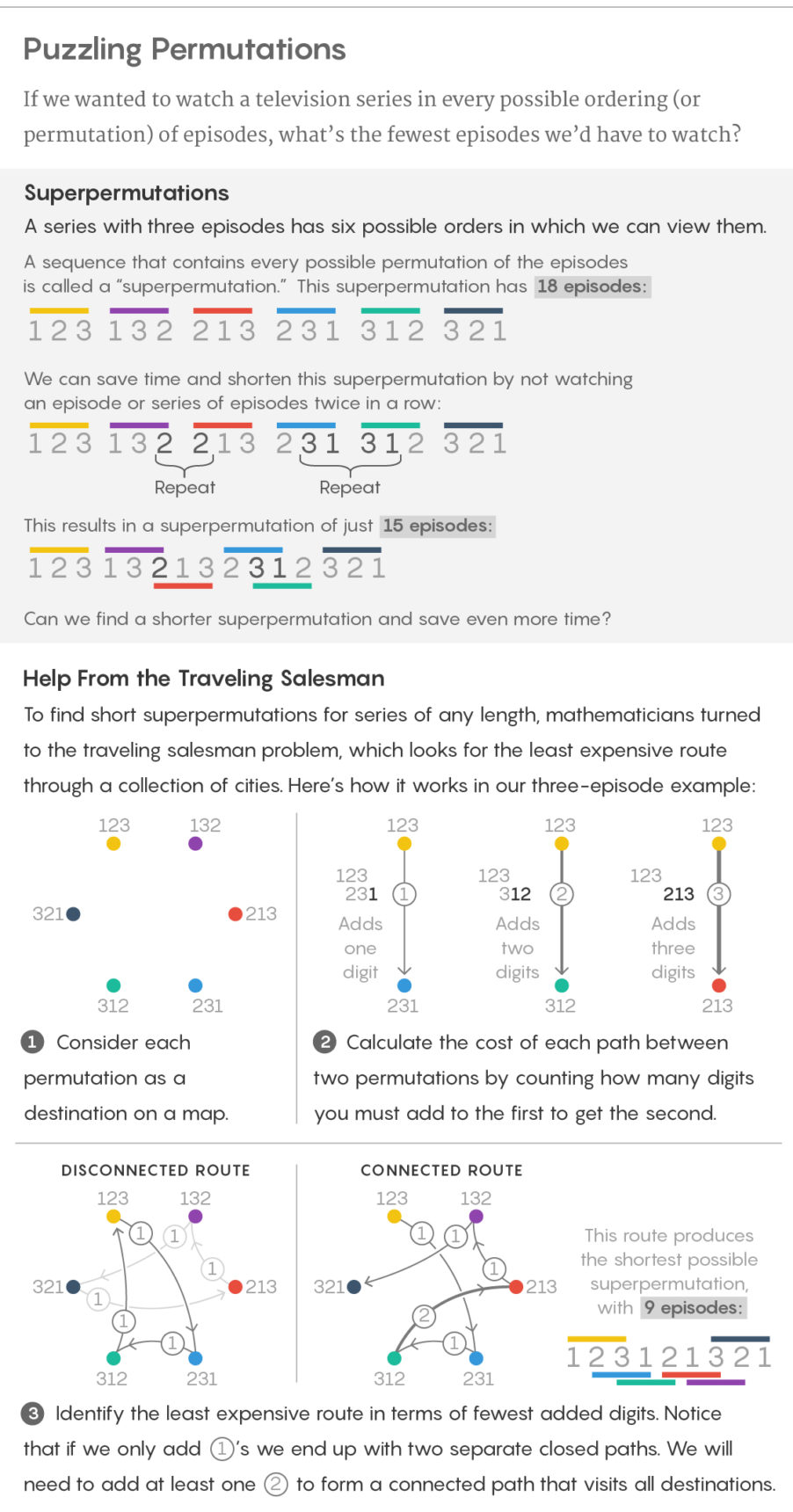
Such a transformation meant that Houston could direct all the capabilities of the algorithms for solving the traveling salesman problem to the super-permutation problem. This task is known for its belonging to the class NP-complex, which means the absence of the existence of an effective algorithm that can solve it in the general case. However, there are algorithms that can effectively solve some types of problems, and other algorithms can produce good approximate solutions. Houston used one of the latter to produce a super-permutation of a length of 872 digits.
Since he gave only an approximate solution, it may not even be the most ideal super-permutation. Mathematicians are now conducting a 3D computational search for the shortest 6-character super-permutation, Panton said. “We know that our search will end in a finite time, but we don’t know if it will take a week or a million years,” he said. “There is no progress indicator.”
Wrong order
By the time Houston came to work, an anonymous post on 4chan had been sitting in his corner of the Internet for almost three years. One mathematician, Nathaniel Johnston of Mount Ellison University, noticed a copy of this post on another site a few days after this entry appeared - not because he was an anime lover, but because he entered different queries on Google, associated with super-permutations.
Johnston read the evidence and it seemed reliable to him, but he did not waste his energy on thorough verification. At that time, mathematicians believed that the factorial formula for super-permutations was most likely correct, and when you think that you know the exact answer to the question, the lower bound on the estimate is of little interest to you. In other words, the episodes of the series about super-permutations went in the wrong order.
After that, Johnston mentioned a lower bound on a couple of websites , but “I don’t think someone paid special attention to this,” he said.
Then, on September 26, 2018, mathematician John Baez of the University of California at Riverside tweeted a post about the opening of Houston from 2014, as part of a series of tweets about obvious mathematical patterns that stop working.
Note Trans.: there was not such a big series of tweets, just three. The other two are also interesting in themselves, although they are not related to this article. One says that 6 is the most popular distance between two neighboring primes for all primes less than 17,427,000,000,000,000,000,000,000. And then this pattern suddenly stops working! The second demonstrates the following connection of integrals, trigonometric functions and the number π

But only for n <9.8 × 10 42 !
His tweet attracted the attention of Egan, who studied mathematics several decades ago, before his career as a recognized science fiction writer began (his first successful story, by happy coincidence, was called "City of Permutations"). “I have never ceased to be interested in mathematics,” wrote Egan by mail.
Egan wondered if it was possible to create a super-permutation even shorter than that of Houston. He plunged into the study of literature on how to create shortcuts in the networks of permutations, and after a few weeks he found what he needed. For a couple of days, he derived a new upper bound for the length of the shortest super-permutation of n characters: n! + (n - 1)! + (n - 2)! + (n - 3)! + n - 3. It is similar to the factorial formula, from which many members are excluded.
"It completely broke the previous upper limit," said Houston.
The lower bound of the author of the post on 4chan was seductively close to the new upper boundary: n! + (n - 1)! + (n - 2)! + n - 3. After the result was published, Egan Johnston reminded mathematicians of the proof of an anonymous author, and Houston with Panton soon proved its correctness. As in the work of Houston, the new lower and upper bounds approach super-permutations from the point of view of the traveling salesman problem: the lower boundary shows that the path through all cities must pass through some minimum number of paths worth more than $ 1, and the upper boundary creates a special path for each n, using only connections worth $ 1 and $ 2.
Now researchers are trying to bring the upper and lower bounds together, and to find a single formula that solves the problem of super-permutation. “Probably, in the end, people will still solve this riddle,” predicted Baez. “Now everything looks good.”
For Haruhi fans, Egan’s solution gives precise instructions on how to view all the possible options for the order of the first season, using a total of 93,924,230,411. You can start browsing today, or you can wait until the mathematicians can still cut that number. The lower bound from an anonymous author proves that this cuts will not save them more than 40 million episodes - however, this is enough to start preparing for the second season.
