How does the barcode work?
Hi, Habr!
Modern man faces bar codes every day without even thinking about it. When we buy products in the supermarket, their codes are read using a bar code. Also parcels, goods in warehouses, and so on and so forth. However, few people know how it really works.
How does the barcode work, and what is encoded in this picture?

Let's try to figure it out, at the same time we will write a decoder of such codes.
The use of bar codes has a long history. The first attempts at automation began in the 50s, a patent for a code reader was obtained in 1952. The engineer involved in sorting cars on the railroad wanted to simplify the process. The idea was obvious - to encode the number using strips and read them using photocells. In 1962, codes were officially used to identify wagons on American railways (the KarTrak system), in 1968, the searchlight was replaced by a laser beam, which increased the accuracy and reduced the size of the reader. In 1973, the “Universal Product Code” format appeared, and in 1974 the first product was sold (using Wrigley's chewing gum — this is the United States;) at the supermarket. In 1984, a third of the stores used streches, in Russia they began to be used from about the 90s.
Quite a lot of different codes are being used for different tasks now, for example, the “12345678” sequence can be represented in such ways (and this is not all):

Let's start a bit-wise analysis. Further, everything written below will refer to the “Code-128” type - simply because its format is fairly simple and straightforward. Those who want to experiment with other species can openonline generator and see for yourself.
At first glance, the barcode seems to be just a random sequence of lines, in fact, its structure is clearly fixed:

1 - The empty space necessary to clearly define the beginning of the code
2 - The start symbol. For Code-128, there are 3 options (called A, B, and C): 11010000100, 11010010000 or 11010011100, they correspond to different code tables (for more details, see Wikipedia ).
3 - Actually the code containing the data we need
4 - Checksum
5 - Stop symbol. For Code-128, this is 1100011101011.
6 (1) - Empty space.
Now how bits are coded. It's all very simple - if you take the width of the thinnest line for "1", then the line of double width will give the code "11", triple "111", and so on. The empty space will be “0” or “00” or “000” on the same principle. Those interested can compare the starting code in the picture to make sure that the rule is being fulfilled.
Now you can start programming.
In principle, this is the most difficult part, and of course, algorithmically it can be implemented in different ways. I'm not sure that the algorithm below is optimal, but for a learning example it is quite enough.
To begin, load the image, stretch it to the width, take a horizontal line from the middle of the image, convert it to b / w and load it into an array.
On the barcode, black corresponds to “1”, and in RGB, vice versa, 0, so the array needs to be inverted. At the same time we calculate the average value.
Run the program to make sure that the barcode is loaded correctly:
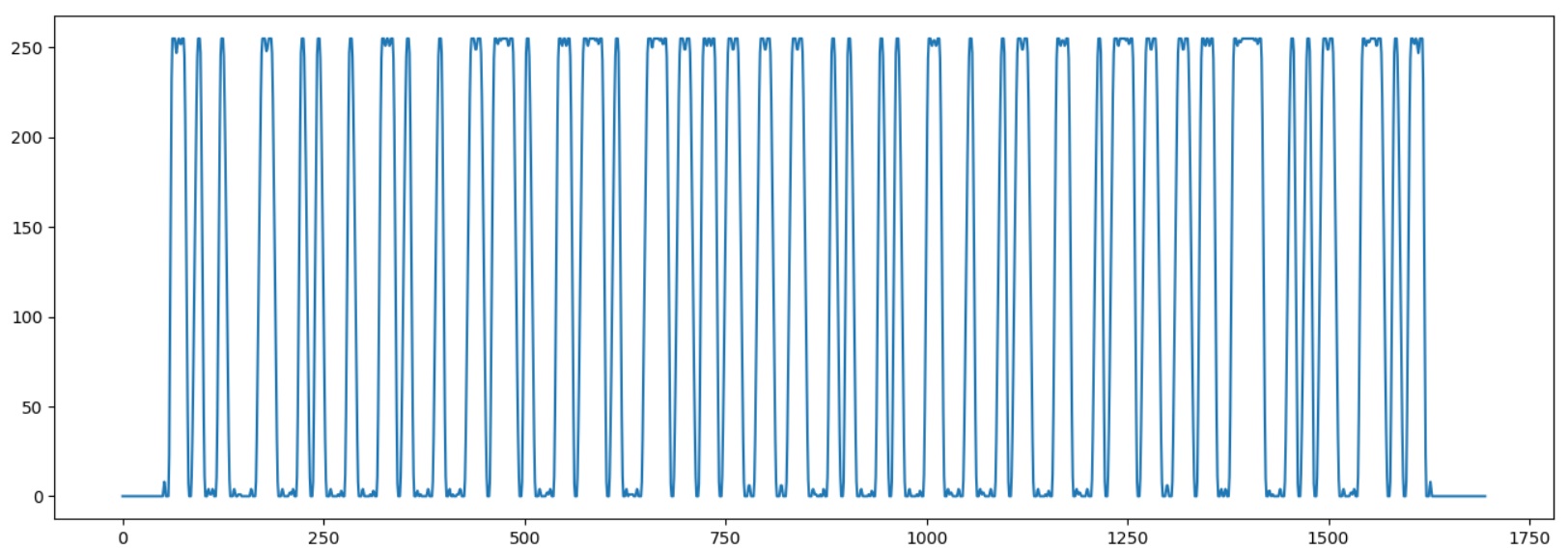
Now you need to determine the width of one “bit”. To do this, we will select the beginning of the starting sequence "1101", recording the moments of the transition of the graph through the middle line.
We write only the transitions through the middle, so the code "1101" will be written as "101", but this is enough for us to know its width in pixels.
Now the actual decoding. We find the next transition through the middle, and determine the number of bits that fall into the interval. Since the match is not absolute (the code may be slightly bent or stretched), we use rounding.
Not sure that this is the best option, perhaps there is a better way, anyone can write in the comments.
If everything was done correctly, then we get approximately the following output:
There are no difficulties in principle, no. The characters in Code-128 are encoded with an 11-bit code that has 3 variations (A, B and C) and can store either different character encodings or numbers from 00 to 99.
In our case, the beginning of the sequence is 11010010000, which corresponds to "Code B ". It was terribly broke to manually enter all the codes from Wikipedia, so the table was simply copied from the browser and its parsing was also made in Python (hint: you shouldn’t do this in production).
Now the simplest is left. We divide our bit sequence into 11-character blocks:
Finally, we form a string and display it on the screen:
The answer to what is encoded in the table will not be given, let it be homework for readers (the use of ready-made programs for smartphones will be considered cheating :).
The code also does not implement a CRC check, anyone can do it themselves.
Of course, the algorithm is imperfect, and was written in half an hour. For more professional purposes there are ready-made libraries, for example pyzbar . Code using such a library takes only 4 lines:
(you must first install the library by entering the "pip install pyzbar" command)
Addition : the user vinograd19 wrote about the CRC count in the comments : The
check digit history is interesting. It originated evolutionarily.
The check digit is needed in order to avoid incorrect decoding. If the barcode was 1234, and it was recognized as 7234, then a validation is needed, which will prevent the replacement of 1 by 7. Validation may be inaccurate so that at least 90% of non-valid numbers are determined in advance.
1st approach: Let's just take the amount. So that the remainder of the division by 10 was 0. Well, that is, the first 12 characters carry the information load, and the last digit is chosen so that the sum of the digits is divided by 10. We decode the sequence, if the sum is not divisible by ten, then it is decoded with a bug this one more time. For example, code 1234 is valid. 1 + 2 + 3 + 4 = 10. Code 1216 is also valid, but 1218 is not.
This avoids problems with automation. However, at the time of the creation of bar codes, there was a fallback in the form of stuffing the number on the keys. And there is a bad case: if you change the order of two digits, the checksum does not change, and this is bad. That is, if barcode 1234 was hammered in as 2134, the checksum will converge, but the number we got is wrong. It turns out that the wrong order of numbers - this is a common case, if you knock on the keys quickly.
2nd approach. Well, let's make the amount a little more complicated. So that numbers on even places are counted twice. Then, when changing the order, the amount just does not converge to the desired. For example, the code 2364 is valid (2 + 3 + 3 + 6 + 4 + 4 = 20), and the code 3264 is non-valid (3+ 2 + 2 + 6 + 4 + 4 = 19). But this turned out to be another bad example. Some keyboards have ten numbers arranged in two rows. the first row is 12345 and below it is the second second row 67890. If instead of pressing key “1” you press key “2” to the right, then the checksum will warn you about incorrect input. But if instead of pressing the "1" key below, press the "6" key - it may not warn you. After all, 6 = 1 + 5, and in the case when this figure is in an even place when calculating the checksum, we have 2 * 6 = 2 * 1 + 2 * 5. That is, the checksum has increased by exactly 10, so its last figure has not changed. For example, checksums Kodv 2134 and 2634 are the same. The same mistake will happen if instead of 2 we press 7, instead of 3 we press 8 and so on.
3rd approach. Ok, let's take something again, just the numbers that stand in even places will be taken into account ... three times. That is, code 1234565 is valid, because 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 + 5 = 50.
The described method became the standard for calculating the EAN13 checksum with minor edits: the number of digits became fixed and 13 where the 13th is the same check digit. Numbers on odd places are counted three times, on even places - once.
As you can see, even such a simple thing as a barcode has a lot of interesting in it. By the way, another life hack for those who read to here - the text under the barcode (if there is one) completely duplicates its content. This is done so that in case of unreadable code, the operator can enter it manually. So, it’s usually easy to find the contents of a barcode - just look at the text below it.
As suggested in the comments, the most popular in trade is the EAN-13 code, the bit encoding is the same there, and anyone can see the structure of symbols on their own .
If readers have not lost interest, one can separately consider QR codes.
Thanks for attention.
Modern man faces bar codes every day without even thinking about it. When we buy products in the supermarket, their codes are read using a bar code. Also parcels, goods in warehouses, and so on and so forth. However, few people know how it really works.
How does the barcode work, and what is encoded in this picture?

Let's try to figure it out, at the same time we will write a decoder of such codes.
Introduction
The use of bar codes has a long history. The first attempts at automation began in the 50s, a patent for a code reader was obtained in 1952. The engineer involved in sorting cars on the railroad wanted to simplify the process. The idea was obvious - to encode the number using strips and read them using photocells. In 1962, codes were officially used to identify wagons on American railways (the KarTrak system), in 1968, the searchlight was replaced by a laser beam, which increased the accuracy and reduced the size of the reader. In 1973, the “Universal Product Code” format appeared, and in 1974 the first product was sold (using Wrigley's chewing gum — this is the United States;) at the supermarket. In 1984, a third of the stores used streches, in Russia they began to be used from about the 90s.
Quite a lot of different codes are being used for different tasks now, for example, the “12345678” sequence can be represented in such ways (and this is not all):

Let's start a bit-wise analysis. Further, everything written below will refer to the “Code-128” type - simply because its format is fairly simple and straightforward. Those who want to experiment with other species can openonline generator and see for yourself.
At first glance, the barcode seems to be just a random sequence of lines, in fact, its structure is clearly fixed:

1 - The empty space necessary to clearly define the beginning of the code
2 - The start symbol. For Code-128, there are 3 options (called A, B, and C): 11010000100, 11010010000 or 11010011100, they correspond to different code tables (for more details, see Wikipedia ).
3 - Actually the code containing the data we need
4 - Checksum
5 - Stop symbol. For Code-128, this is 1100011101011.
6 (1) - Empty space.
Now how bits are coded. It's all very simple - if you take the width of the thinnest line for "1", then the line of double width will give the code "11", triple "111", and so on. The empty space will be “0” or “00” or “000” on the same principle. Those interested can compare the starting code in the picture to make sure that the rule is being fulfilled.
Now you can start programming.
Get the bit sequence
In principle, this is the most difficult part, and of course, algorithmically it can be implemented in different ways. I'm not sure that the algorithm below is optimal, but for a learning example it is quite enough.
To begin, load the image, stretch it to the width, take a horizontal line from the middle of the image, convert it to b / w and load it into an array.
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
image_path = "barcode.jpg"
img = Image.open(image_path)
width, height = img.size
basewidth = 4*width
img = img.resize((basewidth, height), Image.ANTIALIAS)
hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L')
hor_data = np.asarray(hor_line_bw, dtype="int32")[0]
On the barcode, black corresponds to “1”, and in RGB, vice versa, 0, so the array needs to be inverted. At the same time we calculate the average value.
hor_data = 255 - hor_data
avg = np.average(hor_data)
plt.plot(hor_data)
plt.show()
Run the program to make sure that the barcode is loaded correctly:

Now you need to determine the width of one “bit”. To do this, we will select the beginning of the starting sequence "1101", recording the moments of the transition of the graph through the middle line.
pos1, pos2 = -1, -1
bits = ""for p in range(basewidth - 2):
if hor_data[p] < avg and hor_data[p + 1] > avg:
bits += "1"if pos1 == -1:
pos1 = p
if bits == "101":
pos2 = p
breakif hor_data[p] > avg and hor_data[p + 1] < avg:
bits += "0"
bit_width = int((pos2 - pos1)/3)
We write only the transitions through the middle, so the code "1101" will be written as "101", but this is enough for us to know its width in pixels.
Now the actual decoding. We find the next transition through the middle, and determine the number of bits that fall into the interval. Since the match is not absolute (the code may be slightly bent or stretched), we use rounding.
bits = ""for p in range(basewidth - 2):
if hor_data[p] > avg and hor_data[p + 1] < avg:
interval = p - pos1
cnt = interval/bit_width
bits += "1"*int(round(cnt))
pos1 = p
if hor_data[p] < avg and hor_data[p + 1] > avg:
interval = p - pos1
cnt = interval/bit_width
bits += "0"*int(round(cnt))
pos1 = p
Not sure that this is the best option, perhaps there is a better way, anyone can write in the comments.
If everything was done correctly, then we get approximately the following output:
11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011Decoding
There are no difficulties in principle, no. The characters in Code-128 are encoded with an 11-bit code that has 3 variations (A, B and C) and can store either different character encodings or numbers from 00 to 99.
In our case, the beginning of the sequence is 11010010000, which corresponds to "Code B ". It was terribly broke to manually enter all the codes from Wikipedia, so the table was simply copied from the browser and its parsing was also made in Python (hint: you shouldn’t do this in production).
CODE128_CHART = """
0 _ _ 00 32 S 11011001100 212222
1 ! ! 01 33 ! 11001101100 222122
2 " " 02 34 " 11001100110 222221
3 # # 03 35 # 10010011000 121223
...
93 GS } 93 125 } 10100011110 111341
94 RS ~ 94 126 ~ 10001011110 131141
103 Start Start A 208 SCA 11010000100 211412
104 Start Start B 209 SCB 11010010000 211214
105 Start Start C 210 SCC 11010011100 211232
106 Stop Stop - - - 11000111010 233111""".split()
SYMBOLS = [value for value in CODE128_CHART[6::8]]
VALUESB = [value for value in CODE128_CHART[2::8]]
CODE128B = dict(zip(SYMBOLS, VALUESB))
Now the simplest is left. We divide our bit sequence into 11-character blocks:
sym_len = 11
symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)]
Finally, we form a string and display it on the screen:
str_out = ""for sym in symbols:
if CODE128A[sym] == 'Start':
continueif CODE128A[sym] == 'Stop':
break
str_out += CODE128A[sym]
print(" ", sym, CODE128A[sym])
print("Str:", str_out)
The answer to what is encoded in the table will not be given, let it be homework for readers (the use of ready-made programs for smartphones will be considered cheating :).
The code also does not implement a CRC check, anyone can do it themselves.
Of course, the algorithm is imperfect, and was written in half an hour. For more professional purposes there are ready-made libraries, for example pyzbar . Code using such a library takes only 4 lines:
from pyzbar.pyzbar import decode
img = Image.open(image_path)
decode = decode(img)
print(decode)
(you must first install the library by entering the "pip install pyzbar" command)
Addition : the user vinograd19 wrote about the CRC count in the comments : The
check digit history is interesting. It originated evolutionarily.
The check digit is needed in order to avoid incorrect decoding. If the barcode was 1234, and it was recognized as 7234, then a validation is needed, which will prevent the replacement of 1 by 7. Validation may be inaccurate so that at least 90% of non-valid numbers are determined in advance.
1st approach: Let's just take the amount. So that the remainder of the division by 10 was 0. Well, that is, the first 12 characters carry the information load, and the last digit is chosen so that the sum of the digits is divided by 10. We decode the sequence, if the sum is not divisible by ten, then it is decoded with a bug this one more time. For example, code 1234 is valid. 1 + 2 + 3 + 4 = 10. Code 1216 is also valid, but 1218 is not.
This avoids problems with automation. However, at the time of the creation of bar codes, there was a fallback in the form of stuffing the number on the keys. And there is a bad case: if you change the order of two digits, the checksum does not change, and this is bad. That is, if barcode 1234 was hammered in as 2134, the checksum will converge, but the number we got is wrong. It turns out that the wrong order of numbers - this is a common case, if you knock on the keys quickly.
2nd approach. Well, let's make the amount a little more complicated. So that numbers on even places are counted twice. Then, when changing the order, the amount just does not converge to the desired. For example, the code 2364 is valid (2 + 3 + 3 + 6 + 4 + 4 = 20), and the code 3264 is non-valid (3+ 2 + 2 + 6 + 4 + 4 = 19). But this turned out to be another bad example. Some keyboards have ten numbers arranged in two rows. the first row is 12345 and below it is the second second row 67890. If instead of pressing key “1” you press key “2” to the right, then the checksum will warn you about incorrect input. But if instead of pressing the "1" key below, press the "6" key - it may not warn you. After all, 6 = 1 + 5, and in the case when this figure is in an even place when calculating the checksum, we have 2 * 6 = 2 * 1 + 2 * 5. That is, the checksum has increased by exactly 10, so its last figure has not changed. For example, checksums Kodv 2134 and 2634 are the same. The same mistake will happen if instead of 2 we press 7, instead of 3 we press 8 and so on.
3rd approach. Ok, let's take something again, just the numbers that stand in even places will be taken into account ... three times. That is, code 1234565 is valid, because 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 + 5 = 50.
The described method became the standard for calculating the EAN13 checksum with minor edits: the number of digits became fixed and 13 where the 13th is the same check digit. Numbers on odd places are counted three times, on even places - once.
Conclusion
As you can see, even such a simple thing as a barcode has a lot of interesting in it. By the way, another life hack for those who read to here - the text under the barcode (if there is one) completely duplicates its content. This is done so that in case of unreadable code, the operator can enter it manually. So, it’s usually easy to find the contents of a barcode - just look at the text below it.
As suggested in the comments, the most popular in trade is the EAN-13 code, the bit encoding is the same there, and anyone can see the structure of symbols on their own .
If readers have not lost interest, one can separately consider QR codes.
Thanks for attention.
