Quantum Checkers - make checkers great again

We added rules based on quantum theory to checkers to make them less predictable and break standard game tactics. This is not just a game, it is an interactive representation of quantum theory with such effects as superposition and quantum entanglement.
Quantum drafts - the fruit of the
In our quantum checkers, each checker behaves like a quantum object, which in practice means the following:
- The player does not know if there really is a checker in the given cell of the field, he sees only the probability of her being in the indicated cell.
- Checkers of the same color do not differ from each other and you, in fact, do not operate with separate checkers.
The meaning and the basic rules of the game remain as in classic checkers - two players, 8x8, you need to eat all the opponent's checkers.
Want to try? Install the free Quantum Checkers from the App Store here .
Quantum rules

As I wrote above, what you see on the board is not really checkers, but their probability of being in a given cell. At the beginning of the game, the probability of finding each checker in its classic starting position is 1 or 100%. To make a move you need to choose the checker with which you want to go, however, unlike the classic checkers, you do not choose where to go. A checker with a cell of your choice goes to all possible cells according to the classic rules of the cell and the probability of finding it in them will change.
For example, if you play green (yes, in quantum checkers we decided to use colors more cheerfully) and go with a checker from E3 cell, then the state of the board will become like this.
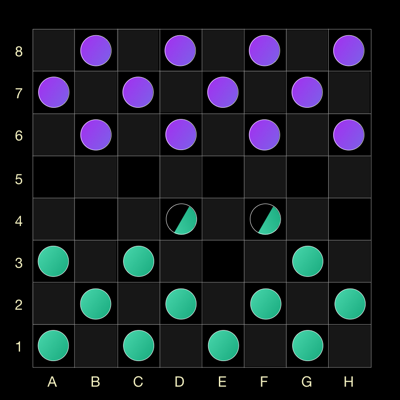
Half a checker means that the probability of being in a given cell is 50%. Why? Because the selected checker could go into any of these cells, which means the probability of its being in each of them is 50%. The result obtained clearly reflects the principle of uncertainty in quantum theory.
Сразу отмечу, что согласно принципу суперпозиции в одной клетке могут находится и шашки разных цветов! В этом случае заполненность шашки определенным цветом будет означать вероятность нахождения шашки этого цвета в данной клетке.Then your opponent walks with his purple sword, for example, with a sword from cell D6 and gets this symmetrical result.
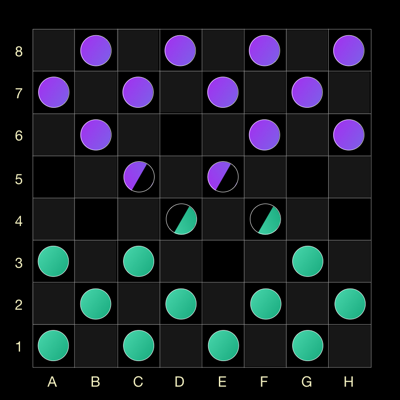
Need to take, you think. Yes, you need to take the opponent’s checker according to the classic rules. And here the magic begins. Let's try to go green checker from cell F4. At the moment when you tap on the cell, the game calculates whether there is a checker in this cell. If the probability is 1, then everything is simple - there is a checker, if it is zero, then it’s also simple - there are no checkers. If the truth is somewhere in the middle, then the game throws a die and thus determines the presence of checkers on the field.
So, we tap. There are two options for the development of events:
- There are no checkers in the selected cell. In this case, you will be asked to go another checker of your color. Yes, in quantum checkers, in a situation where there was actually no checker in the cell you selected (that is, it may be there, but you “measured” this cell, and it turned out that it is not there).
- There is a checker in the selected cell. In this case, it should eat the purple piece and the board will look like this:
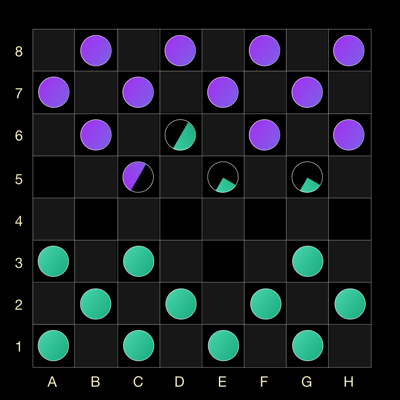
Why does the picture look that way? We had two scenarios:
- The purple checker was in E5 cell and the probability of this was 50%. Then again, with a 50% probability, the green checker will be in cell D6.
- The purple checkers were not in the E5 cell and the probability of this is also 50%. Then the green checker with a probability of 25% will be in the E5 cell and with a 25% probability in the G5 cell.
At the same time, 50% probability of finding the checkers in the C5 cell is preserved. On the board, under your name, the cumulative probability of finding all your checkers on the field is displayed. At the beginning it is equal to 12, since you have only 12 checkers. After the last move, the probability is likely to change, and according to the picture above, the cumulative probability for purple checkers will be 11.5. After all, purple drafts became half as small;)
End of the game
How to win with such uncertainty? In classic checkers, you win when all opponent's checkers are eaten or blocked.
In quantum checkers, both situations can occur with a certain probability and the game ends in one of two cases:
- The aggregate probability of finding the opponent’s checkers on the field has become less than 1.
- All remaining opponent checkers are blocked with a probability greater than 1.
In both cases, you win with some probability, not 100%. A 100% classic win is also possible.
Thus, the strategy of the game is to think in advance how likely your checker will be in a particular field and how it will affect the future game. In contrast to the classic drafts, the variants of the development of events become dramatically more, and it becomes very difficult to calculate the game in advance.
Do not forget to download the game in the App Store and, of course, we are very interested in your feedback!
