How to create a reliable game mechanics in Excel. Part 2

In this part we will solve the problem of optimal placement of weapons on the tank, the spatial location of teleports in the MMORPG and balance the battles of four classes of RPG characters.

Object location tasks

Spreadsheets for this part can be downloaded here: ( SuperTank ) ( teleports, part 1 ) ( teleports, part 2 )

SuperTank: problem solved!

In the first article of the series, we talked about an example of a task for a game called SuperTank. In the second part, we got acquainted with the basic concepts of solution modeling and I talked about solving a simple example using the Search for Solutions tool in Excel.

Now we can apply the knowledge obtained in the second part to the SuperTank task, and prove that with their help this problem can be solved easily and quickly. Refresh your memory: SuperTank is a game in which you can fight in a custom tank. Supertank looks like this:


Each supertank can have any number of guns of five different types:


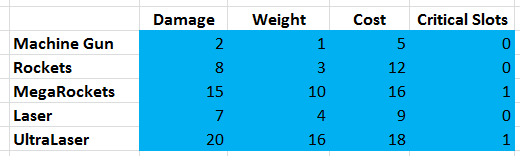
The supertank can fit 50 tons of weapons, and the player can spend 100 credits. Also, the supertank has 3 "critical slots" in which special guns such as the MegaRocket and UltraLaser are placed.

The spreadsheet for this example can be downloaded here .

The goal is to pick up weapons that maximize damage inflicted by supertank, without going beyond the limits of 50 tons, 100 credits and 3 critical slots. We also assume that this table contains all the necessary information, and that factors such as range, frequency, and shooting accuracy are irrelevant or have already been taken into account in the Damage parameter of the corresponding weapon.

To optimize this scheme, we first enter this data into a spreadsheet. Immediately below it, we will add another table, in which there will be a set of 5 "quantitative" cells to indicate the number of each of the 5 types of weapons.

For now we will enter the value 1 in these cells, just to test their work, but these will be our decision cells — we will ask the Solver tool to find the correct values ​​of these cells. You can understand that these are decision cells by the yellow color, because we continue to follow the formatting rules outlined in the second part. To the right of the “quantitative” cells, we will add calculation cells, which will multiply the values ​​of the number in the decision cells by the values ​​of Damage, Weight, Cost and Critical Slots from the table above. Thus, each row of this table will correctly reflect the damage, weight, price and critical slots required for all used guns in all categories of weapons.


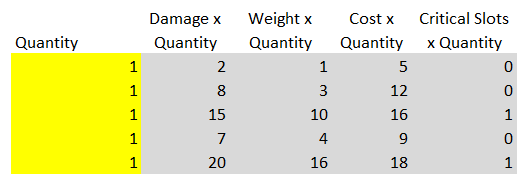
We will also create a section below that summarizes all the values ​​of quantity, weight, cost and critical slots from the table above, and compares with the maximum values ​​of weight, cost and critical slots specified in the problem conditions (50, 100 and 3, respectively).


In accordance with the formatting rules from the second part of the article, the blue cells at the top are the criteria from the conditions of the problem. Gray cells are calculation cells that represent the total values ​​of weight, cost, and critical slots based on the summation from the quantity table (that is, the total values ​​of the columns Weight x Quantity, Cost x Quantity, and Critical Slots x Quantity). Finally, the orange cell represents the total damage of our supertank, based on the total damage of the Damage x Quantity column in the table above.

Before we proceed to the solution, let's make our spreadsheet more user friendly. We will use Excel's ability to give each cell a name and give clear names to the seven cells in the last calculation table. This is optional, but in the long run this will make the spreadsheet look much clearer (for example, if instead of $ F $ 21, the cell is called MaxCriticalSlots). To do this, we simply select the cell and go to the name input field to the left of the formula field, and enter a new name.


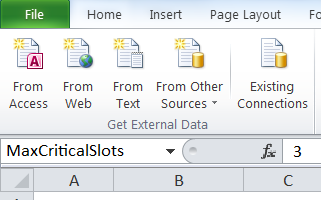
Now let's finally go to Excel Solver and find a solution (go to the right side of the Data tab and select Solver.) If you don’t see it, go to Excel Options , select the Add-Ins category (“Add-ins”), make sure that Excel Add-Ins is selected in the Manage drop-down list, click Go, and make sure that The Solver Add-in checkbox is checked.

In the Set Objective field (Optimize Target Function) we will select the orange target cell, and below we will click on the Max radio button. In the By field Changing Variable Cells (“Changing cells of variables") select decision cells (yellow cells in the Quantity column of the second table). Below, click on the Add button to add the following restrictions:

• The values ​​of the decision cells should be in the range from 0 to some reasonable maximum (we chose 50, even though this is probably a much larger limit value than necessary). It is also necessary to set the restriction "= integer" ("whole") for each cell of the solution, because we cannot have a fractional part of the weapon, and Excel Solver considers each variable as a real number by default, unless you specify the opposite.

• We also need to limit the values ​​of the total cost, total weight and total number of critical slots to the values ​​from the conditions of the problem. The image of the dialog box shows that they now have convenient names that we added to the lower table, making the dialog box easier to read.

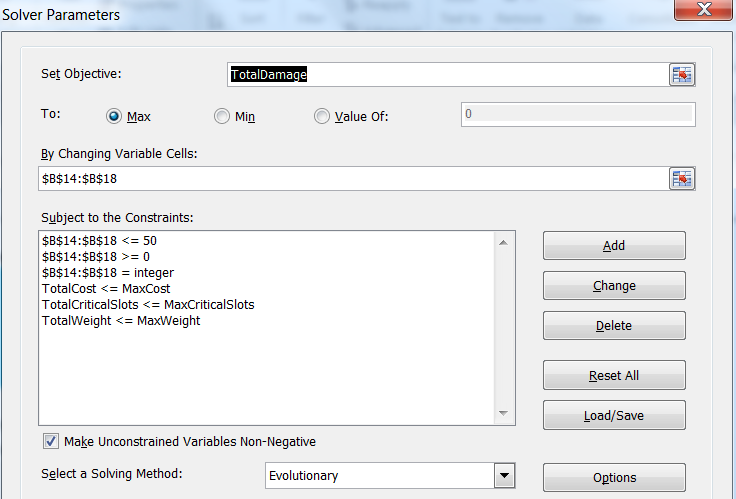
Now we will click on the Solve button (“Find solution”) and after a short wait, Solver will fill in the Quantity values, which will give us the following:

• 1 Machine Gun
• 3 rockets
• 2 MegaRockets
• 1 Laser
• 1 UltraLaser

All this gives us a total loss of 83 units and takes exactly 50 tons, 100 credits and 3 critical slots. You can see that the best solution does not change from the Solver runtime. If you reset these values ​​and re-optimize, or go to Options and change the seed, we still get the same values. We cannot be 100% sure that this solution is optimal, but given the fact that Solver did not manage to improve it after several optimization passes, then with high probability it is a real optimum, and not just a local maximum.

Problem solved!

Additional uses

The great thing here is that we not only solved the task much faster than we would have done manually, but also set it up in such a way that it would allow us to test which weapon in the SuperTank game would be most useful with different parameters (weight, cost, critical slots). This means that we can relatively easily change the effect of various changes on these parameters on the SuperTank game, and if we want to add a new alternative model of supertank, which will be easier, harder or have a different number of critical slots, then this can be done very simply.

By changing all these parameters, we can also get an understanding of the relative usefulness of each of these weapons, and quickly determine which of them is too useful, not enough, has a price that is inappropriate to its weight and damage, and so on.

Again, the point is that such a tool allows us to search the design space much faster than we could manually. It provides us with a convenient opportunity to evaluate the effect of such changes with any incremental design solution that we can come up with, whether it is changing the parameters of the weapon or the supertank itself, adding new weapons or models of supertanks, as well as adding new parameters (let's say the size limit in cubic meters).

To understand what I mean, go to the blue Max Cost cell and change its value from 100 to 99. Now start Solver again and you will get a completely different weapon placement pattern:

• 0 machine guns
• 2 rockets
• 3 MegaRockets
• 3 lasers
• 0 UltraLasers

Such a scheme gives a slightly smaller damage indicator (82 instead of 83), but it is radically different from the previous one.

If we assign the Max Cost value to 101 or 102, and perform the calculation again, then there is a probability that we will get a configuration similar to the first one or coinciding with it; Be that as it may, the damage will remain equal to 83 (the schemes may vary, because in such cases there are several optimal schemes). However, if you set the Max Cost value to 103, then you should get the following:

• 1 Machine Gun
• 4 rockets
• 2 MegaRockets
• 0 lasers
• 1 UltraLaser

That increases the total damage to 84.

This is interesting: such a weapon placement scheme is very different from the first two.


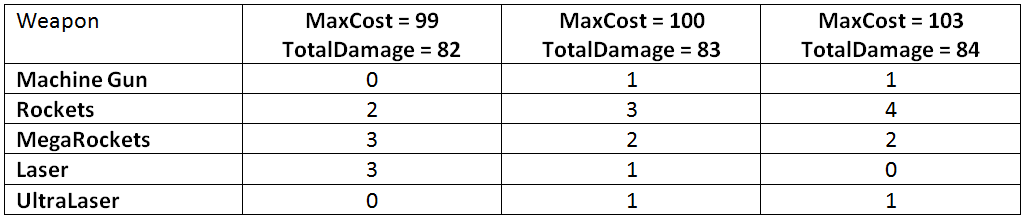
As you see, we get an unexpected result: the optimal choice of weapons in our scheme strongly depends on the parameters of the supertank and can change significantly even with small changes in these parameters. In addition, it gives us all sorts of useful information: all five types of weapons are useful in at least two of the three supertank settings, and the Rockets and MegaRockets are obviously useful in all three. It seems that this tells us that all five types of weapons are well balanced, that is, useful in relation to each other, and at the same time they remain unique.

And as you can also notice, similar modeling and solution optimization provide us with an excellent opportunity to quickly perform a search in a local neighborhood and re-optimization. For some types of tasks, it will allow us to detect the dominant strategies and exploits of players that are difficult or impossible to find in any other way.

Wormhole Teleports

Looking at the last two examples (example with tax rates in a strategic game and SuperTank), you might think that such techniques are applicable only in cases when users deal with numbers. But you will be absolutely wrong! As we will see, there are many examples of the fact that you can benefit from the optimization of design elements that not only do not look like numbers to users, but do not look like them at all!

You may also think that decision modeling is applicable only to decisions that players can make in games. This is also not true: in some cases they can be used for modeling in order to optimize your own solutions as a designer.

Say you're working on a space MMORPG. One day, your lead designer approaches you with visible anxiety on his face. "We are completing the redesign of the Omega sector," he says. “And we had a problem. We are planning to add a few “wormhole” teleports in this segment of the world, but we cannot agree on where to place them. ”

“How many teleports?” You ask.

“We don't know yet. Probably three, but they can be from two to four. We are not sure yet. ” Then he shows you a map that looks like this:


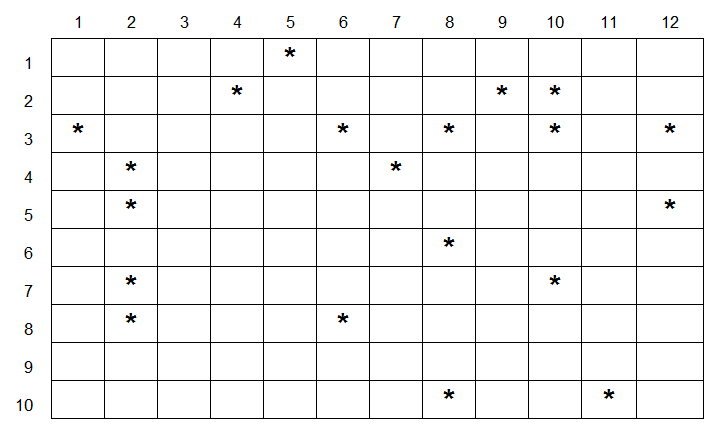
“What is this?” You ask.

“This is a map of the Omega sector. Or at least the star systems that a player can visit in this quadrant. We need to determine in which cells the wormholes should be. ”

“Well, okay, but according to what rules are they placed? Can a wormhole be placed in the same quadrant as the star system? ”

“ We want you to place the wormhole so as to minimize the distance from any star system to the nearest wormhole. And yes, you can put them in the same quadrant as the star system; these are just small teleports hanging in space, so they can be placed anywhere. And remember that we have not yet decided how many there should be, so give me solutions for 2, 3 and 4 "wormholes". ”

How to formulate this problem, and how to solve it?

Optimize teleports!

Let's start by preparing the solution cells. Denote four teleports as A, B, C and D. We know that each teleport is essentially nothing more than the coordinates (x, y) on the star map of the Omega sector. We also know that we will need some way to specify the number of active teleports, so we will add a cell that allows us to set the number of teleports. We use teleport D only when 4 “wormholes” are used, and C - only when we have 3 or more.


Below we will prepare a table for calculating the distance from each star system to the nearest teleport. This table looks like this:


The left blue shows the coordinates of each star system on the map. Each line is one star system. We just transferred them from the Omega sector map, which the leading designer gave us.

On the right, we calculate the distance to each of the four teleports. This is just the Pythagorean theorem. The distance is calculated as the square root of the horizontal and vertical distance between the star system and the teleport:

= SQRT (($ B14-Ax) ^ 2 + ($ C14-Ay) ^ 2)

(Do not worry - I promise that this is the most difficult mathematics we will meet in the series!)

We take the X and Y coordinates of each star system from the blue cells in the table above, and the X and Y coordinates of each teleport (the cells with the names Ax and Ay for teleport A in the above function SQRT ()) - from the yellow cells of the solutions above.

Finally, we take the minimum of these four values ​​in the Dist to Closest column, that is, we simply use the MIN () function to determine the minimum of the four values ​​on the left. Then we summarize the whole column below; sum is the target cell.

You may have noticed that in the screenshot above, all the cells are Dist to D. The reason is that we use the “Number of Teleporters?” Cell in the upper section of the decision model, which allows us to adjust the number of teleports to be counted. If the number of teleports is 2, then we use the value 99 in both Dist to C and Dist to D, and if it is 3, then the value 99 is used only in the Dist to D. column. Due to this, each star system will ignore all the extra teleports. when calculating the distance to the nearest teleport in the case of 2 or 3 teleports.

Now we will launch Solver:


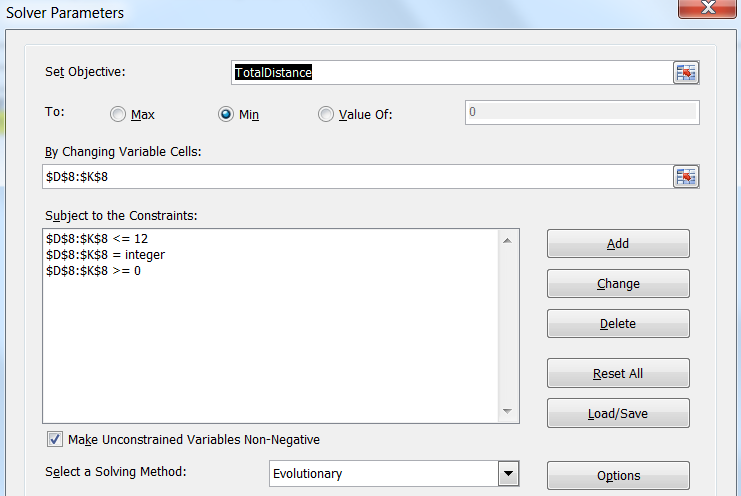
The target cell is the sum at the bottom of the Dist to Closest column. Notice that, unlike other examples, here we want to use the “To: Min” radio button, because we need the minimum distance between all star systems and teleports, and not the maximum.

Below, we will specify eight yellow cells of X and Y coordinates of wormholes A, B, C and D as the decision cells (“By Changing Variable Cells”). In the restrictions section, we limit each of the coordinates as an integer value in the range from 0 to 12. Notice that we use an integer constraint for these decision cells, because we mean that the lead designer just wants to know which cell each teleport will be in, but we can easily skip this constraint if the designer needed real coordinates.

If we set the values ​​of 2, 3, and 4 for “Number of Teleporters?” And sequentially run Solver at each value, we get the following configurations:


With this information, we can go to the lead designer and show him the optimal places for locating any number of teleports in the range from 2 to 4. This is how the optimal location of wormholes for 2, 3 and 4 teleports looks on the map (shown in green).


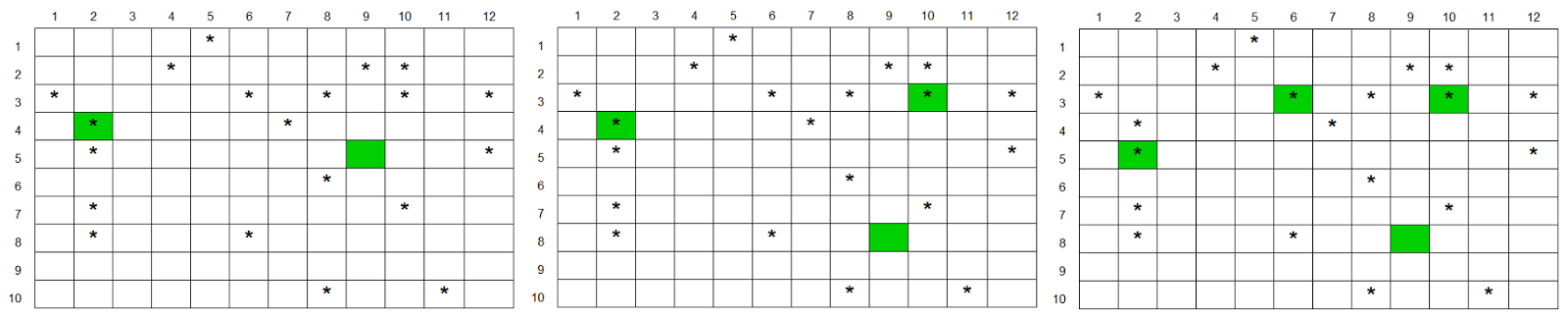
The spreadsheet for this example can be downloaded from here .

Did I talk about ninjas?

“Amazing,” says the lead designer, but you see suffering on his face. “Uh, but I forgot to tell you that some of these systems are populated by space ninjas. And we want systems with ninjas to be further from wormholes, so that players do not feel overly threatened. ”

“Wow. It completely changes things. ”

“Exactly. In addition, in some star systems there are not one, but two colonies, that is, it is twice as important for them to be close to teleports. Or it is twice as important to be further if it is a system with two space ninja colonies. Here is what the map looks like now: "


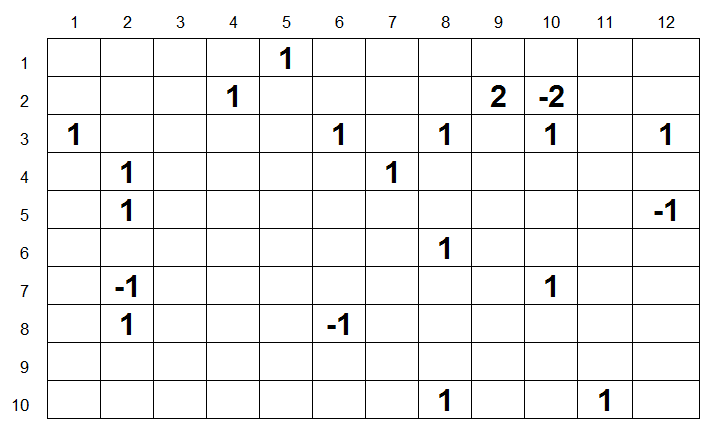
He continues: “Every negative number is a space ninja colony. The system with the number 2 contains two human colonies, and with the number -2 there are two ninja colonies. Can you tell

me where to place the teleporters in this case? ” “ Tell me, have you at least already decided how many teleports will be: 2, 3 or 4? ”, You ask caustically.

"I'm afraid not yet."

We decide taking into account the ninja

To solve this problem, we need to add a new column to the table, indicating the weights of the table. We will call it a multiplier. We will simply multiply this value by the value in the “Dist to Closest” column.

When we do this, Dist to Closest slightly changes its meaning. Now this is not the distance to the nearest star system, because for star systems of ninjas the value changes by a factor of -1. It looks more like generalized "points" (score), so let's call them that.


Thus, points now represent the cumulative value. By minimizing it, we make sure that Solver strives to be as close as possible to systems with human colonies and at the same time as far as possible from populated ninja systems.

Now we get the following results:


As you can see, this gives us the configuration of teleports, in each case very different from simpler versions without ninjas.


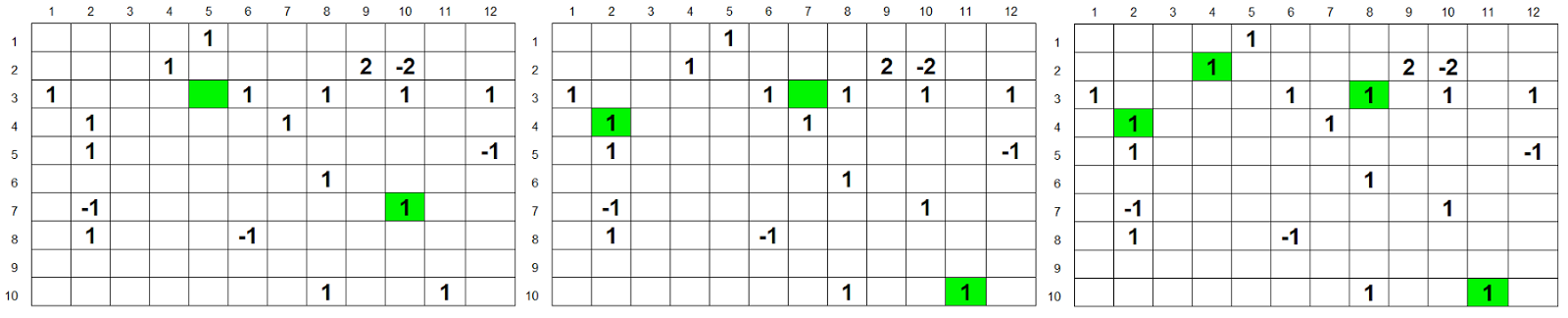
The spreadsheet for this enhanced version of the teleport example can be downloaded from here .

As you can see, our solution model was able to quickly solve this non-trivial task, and we can adapt it to changing requirements.

This task belongs to a class of tasks, called “object location problems”, which are very well studied in the field of operational management. But as you can see, they can potentially be used in game design as well as in level design, and the solution is simple (if not trivial) in Excel.

Balancing classes for battles Player-vs-Player

The spreadsheet for this part can be downloaded from here: link

Spreadsheets and Simulations

In the previous three parts of this series of articles, we became acquainted with the concept of modeling and optimization of solutions, as well as with the tool “Search for solutions” (Solver) of Excel. We showed how they can be used to calculate the optimal city tax rates in 4X strategies, to determine the optimal placement of teleports in the space game and to select the optimal weapon layout for the supertank task described in the first part.

A natural question arises: what about balancing the game? Is it possible to apply such techniques to all kinds of complex balancing tasks that are found in many different types of games, in particular, in strategies, RPG and MMORPG?

The answer to this question: yes, of course, but with many reservations. Spreadsheets in particular have many limitations, because in most non-trivial cases they do not accurately describe the game. Therefore, it will be difficult for us to perform reliable balancing using optimization techniques; the real problems of balancing the vast majority of games will be far beyond what we can model in a spreadsheet. Simulation of the game itself is usually too complicated, it has a lot of “moving parts” and is often performed in real time. When trying to perform a discrete simulation, we can face all sorts of problems.

Therefore, if we wanted to use similar techniques for balancing classes in MMORPGs such as WildStar or in strategic games likePlanetary Annihilation , then to ensure at least some accuracy and usefulness, we would have to integrate them into the game simulation itself.

In addition, the truth is that some aspects of balancing cannot be automated; as we explained in the first part of the article, the feel of the game is not automatically adjustable.

Therefore, the best we can hope for is a demonstration of a simple example that illustrates a general approach to tasks of this type: with a simple example in Excel, we will learn how to approach and optimize this type of balancing problem. We show that, at least for an example of simple combat, Solver can do a good balance of several RPG classes relative to each other. Then you can use this basic structure as the basis for solving such optimization problems with a more complex scheme and deeper integrated into the simulation of the game.

We hope that with us you will learn all the tricks and see what this simple example can give us.

Balancing not defined

There is no single, generally accepted definition of the word "balancing." It has many meanings, and the true one usually depends on the context of the game in question. In different conditions, balancing can be associated with setting up several classes of characters in order to equalize their capabilities in a role-playing game, with the number of opposing forces fighting against each other in a strategic game, or with adjusting the cost of different units or resources in accordance with their usefulness.

The best definition of "balancing" usually depends on the design goals of the game in question, but since these goals can be any, it is impossible a priori to determine what balancing actually means for games in general.

Some players tend to think that balancing in battle means equal damage. This is especially true for MMORPGs where players often complain that damage per second (DPS) of one class is too small or too large relative to others.

Of course, classes cannot be balanced only by DPS; It is acceptable for one class to have more DPS than the other, but this should be compensated for by other factors that limit the overall utility of the class, for example, reduced survival or less long-term DPS compared to short-term DPS.

Tiny MMO

Imagine that we are creating a new project, a very simplified multiplayer massively online role-playing game called “Tiny MMO”. As part of the design, we strive to balance the four classes for player versus player (PVP) battles so that all four classes are relatively equal in battle against each other, and so that there is no obvious "best" or "worst" class that You can fight against other classes.

Although “Tiny MMO” is a real-time game, the action of each player lasts exactly 3 seconds, so we can sample it, presenting it as a turn-based game in which each turn is a three-second gameplay.

Players in this game can choose one of four classes of characters:

• Warrior (Warrior) deals the most damage
• Mage casts spells at a distance and has the greatest attack range from all four classes.
• Healer (Healer) is automatically treated, restoring for each move a certain part of their health
• Barbarian (Barbarian) has the most health

This is all that we know about these four classes, and we need to set the initial parameters for health (HP), damage, healing and attack range for all four classes. We need to balance them so that each class is unique and its characteristics are significantly different from all other classes, but as a result, each class is as "balanced" as possible with respect to the three others.

In other words, we aim to optimize the following table:


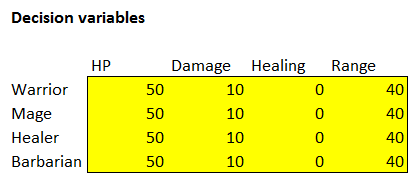
For now, we use temporary values ​​and assume that each class starts with 50 HP, deals 10 points of damage per turn, cures 0 HP per turn, and has an attack range of 40 meters. Each character moves at a speed of 10 meters per turn. Since the design states that all four classes of characters can move at the same speed, we will consider this value to be constant, and we will not enter the movement speed in the table of decision variables.

Obviously, this is a training example with a very simplified damage model. This is a continuous average damage value per second, which ignores the differences in impulse damage from long-term damage, as well as mana and other mechanics that modify the class's attacking abilities. We will only have one type of damage, which is rather unrealistic, because most classes have dozens of types of damage, and we will need to implement an AI system that selects an attack in each turn. In addition, in most games, the damage has an element of chance, but for the time being we will omit it and assume that the variability of the damage is not so great as to significantly influence the outcome of the battle between the two classes.

Of course, any balancing performed in Excel is unlikely to be perfect or in line with the final balance of the game; she will have to go through many iterations of playtests. But if we spend one or two hours on getting a good first option for our Excel game, at least we are much more likely to get closer to the quality parameters of the initial balance, which will bring us closer to the final balance we want to get.

Table wins

We need to balance the four classes with each other in a one-on-one battle. Since we only have 4 classes (Warrior, Mage, Healer and Barbarian), there are a total of 6 possible combinations of different classes:

• Warrior - Mage
• Warrior - Healer
• Warrior - Barbarian
• Mage - Healer
• Mage - Barbarian
• Healer - Barbarian

Such balancing can be quite complicated. Even in our rather simple case with four classes, we got six interclass relations, just as we can draw six lines between four points of a square.


Every time we want to make even a small change in one of the parameters of any of the classes, this change will also affect the balancing of PvP between this pair of classes and the other two classes. This power interconnectivity with an increase in the number of classes will only grow, and decisions about balancing PvP between any pair of classes made “in vacuum”, without taking into account all other interactions, can become very dangerous.

Ideally, we would like to create a certain table of victories.like the one shown below. If we can simulate a fight between each of these 6 pairs in a spreadsheet, then we will be able to generate some kind of “points” variable for each of the 6 pairs. The more points the better, so we can combine all these six points to generate a goal function.


Notice that in the table shown above, the cells along the diagonals are zero, because they denote pairs of the same class, which will be balanced by definition. In addition, the cells in the upper right corner are also zero, because they denote exactly the same pairs as in the cells in the lower left.

Now let's prepare a model for the battle between two different classes.

"Battle Simulator"

Place each pair of classes at a distance of 100 meters from each other. Each character has 3 seconds to attack, so we can present it as a step-by-step simulation, in which each “move” means 3 seconds. On each “move”, each character either attacks the other, if he is within the range of the attack, or continues to move in order to shorten the distance.

The simulation looks like this:


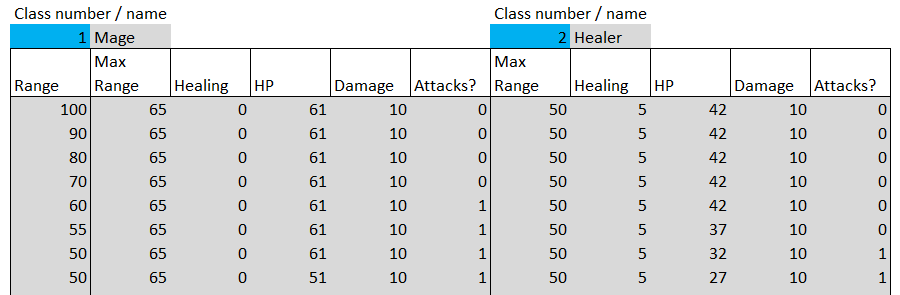
Above shows a pair of characters who joined the battle: in this case it is Mage (class 1) and Healer (class 2). The left column shows the current distance between two simulated characters.

For each character, the columns will be:

• Max Range : This is the maximum distance at which a character can attack. It is taken directly from the yellow decision variables in the decision variable table.
• Healing : This is the amount of character treatment per turn, obtained directly from the decision variable table.
• HP : This is a character's health in each turn. Initially, it is equal to the corresponding value of HP from the decision variable table, but it decreases with time when another character attacks. It also increases in each turn by the amount of treatment that a character can apply to himself in each turn.
• Damage : the amount of damage a character causes to an enemy when he is within range of attack. When a character dies, this value drops to 0.
• Attacks? : This column checks if the character is within range of attack. If so, it will mean that in the current course the character attacks; if not, the character moves closer to get to the other character.

Thus, both characters begin to move toward each other, and then attack, until one or both of them die. Each character moves every 3 seconds for 5 meters (5 meters per “turn”). When both characters move towards each other, the Range will change in each turn by 10 units, and by 5 units, if only one of them moves. The game itself is structured so that both characters can start moving at the same time, after which the move is allowed at the same time, so it is possible that both characters can die at the same time.

Next, we need to set up scoring for this table and generate a numerical value indicating how “good” the fight was; in other words, how close we are to achieving our design goals.

Obviously, we want both characters to be dead by the end of the battle, or at least as close to death as possible. If the battle is balanced, then both of the fighting classes should minimize the health of the enemy at the end of the battle.

However, this alone is not enough. If we organize the scoring in this way, the optimizer will simply maximize the damage values ​​so that both characters instantly kill each other! (If you're curious, try changing the spreadsheet attached to the article to see for yourself.) Obviously, we are not aiming for instant death: we need both characters to be dead or almost dead by the end of the battle, but at the same time we want the battle to last a reasonable amount of time.

In other words, we are not only striving to ensure a relatively equal balancing of all classes against each other; we also want to make the balance interesting , including the battles lasting the appropriate amount of time.

To generate such a balance estimate, we need to create several cells to the right of each table. Duration indicates the duration of the battle; it counts the number of rows in the table in which both characters are still alive. Total HP calculates the total hit points of the two surviving characters. Ideally, it should be 0, that is, by the time the battle ends, both characters die.


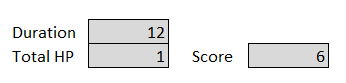
I. Finally, Score combines the duration and total amount of hit points in the form (Duration / (1 + Total HP)). Note that we added 1 to the divisor, because Total HP can be equal to 0, and in that case we would get a divide-by-zero error. Thus, we can guarantee that we reward the optimizer for finding the maximum battle duration and the minimum value of the sum of hit points.

(Note that since in each “simulation” of class versus class we have 17 lines. This means that we essentially made a design decision that the battle should last about 17 rounds. If we want the battle to be shorter or longer, you can change the number of rows, edit the formulas for estimating the score accordingly and perform the re-optimization.)

Finally, we take these six Score values ​​(one for each table) and use them in the above Victory Table to show the results of the battle between each of the pairs of classes.

You can simply summarize these six scores and use the result as the final Score value. However, if we do this, Solver will most likely not be able to find a good balance between the highest and lowest grades for individual battles, and also receive very high marks for some pairs of classes and low marks for others. We do not want this: we need all the grades to be high and we strive to raise them all. To fix this, we multiply the sum of the estimates by the smallest group evaluation (using the Excel MIN () function) to get Solver to focus on the estimates with the lowest value.

Add restrictions

We have not finished yet. If you optimize the decision model with the current parameters, then most likely the classes will be configured incorrectly - in fact, it is highly likely that the model will write the same values ​​of HP, Damage, Healing and Range into the table of decision variables.

And we, of course, want each class to have its own individuality. We need Warrior to do the most damage, Mage has the largest Range, Healer has the highest Healing value, and Barbarian has the most HP. We also want these differences not to be too small - we need these classes to be very different from each other.

To do this, we will create a small table of restrictions. This table ensures that each of the four classes will have a corresponding attribute, and then give a rating of 0 or 1, depending on whether the restriction condition is satisfied.


The Min difference table on the right indicates the minimum difference of each class attribute relative to all other classes. In other words, Warrior should have at least 4 HP more damage than all other classes, Mage should have an attack range of at least 10 more, and so on.

Now that we have added these special limitations, it is time to optimize!

Searching of decisions

Now we can run Excel's built-in Solver tool (“Search for Solutions”) to try to optimize the initial parameters. As the goal cell, we will select the Score cell, which combines the results of all six tournaments. We set the decision variables to include all 16 cells in the yellow Decision variables table that we created at the beginning.

We also set constraints (in the Subject to the Constraints field) as follows:

• All decision cells must be integers with a minimum value of 0.
• All cells in the HP column should have a maximum value of 200 and a minimum of 30.
• All cells in the Damage column have a maximum value of 20.
• All cells in the Healing column have a maximum value of 15.
• All cells in the Range column have a maximum value of 100.
• In addition, all four cells in a particular section of the Constraints must be set to 1 in order for their special conditions to be satisfied.

Finally, select the Evolutionary value for the Solving Method and launch Solver. Consider, since this is an evolutionary algorithm, there is a possibility of improving the solution found during the second or third Solver run, or after setting the parameters (the Options button) for evolutionary optimization.

As a result, we should have something like this:


... and how magically Solver gave us a good initial balance configuration.

As you can see, Warrior now deals the most damage, the Mage has the greatest range, the Healer heals the best, and the Barbarian has the most HP. In addition, you can go down to the results of individual “class versus class” tournaments and see how classes have manifested themselves in battle with each other; as you can see, most of them are balanced very evenly - by the end of the battle both classes die, or one of them barely survives. In addition, all tournaments last long enough, none of the classes can not "voshotny" the other.

Not bad for a few hours, right?

Conclusion

In this example, we created a simple balancing problem and demonstrated that in fact we can solve it using simulation and optimization. Although it is obvious that this is a simple example, it shows us the power of modeling and optimization techniques for solutions. In addition, it can be a source of inspiration that can be used in more complex balancing tools, which are closely integrated into the simulation of the game. We hope that you can use this example as a guide to the formulation of such tasks in practice.

In the next two parts of the series we will plunge into the field of assignment problems, which is associated with the choice of optimal assignments from two or more sets of entities. We will show how to solve these types of tasks and demonstrate how this approach was used to create the design of the towers in our strategic game for iOS / Android City Conquest .