Let's remove quaternions from all 3D engines.
- Transfer
Graphic programmers use quaternions to record three-dimensional turns . However, it is difficult to understand quaternions because they study them superficially . We just take on faith strange multiplication tables and other mysterious definitions, and use them as “black boxes”, turning vectors as we need. Why and ? Why do we take a vector and turn it into an “imaginary” vector to transform it, for example? But who cares if everything works, right?
There is a way of describing turns called a rotor , which belongs to a region and complex numbers (in 2D), and quaternions (in 3D), and even generalizes to any number of dimensions.
We can create rotors almost completely from scratch , instead of determining quaternions from nothing and trying to explain how they work in hindsight . It takes more time, but it seems to me that it is worth it, because they are much easier to understand!
In addition, to visualize and understand the three-dimensional rotors do not need to use the fourth spatial dimension.
It would be great if they began to force out the use and study of quaternions, replacing them with rotors. It is very easy to replace them, and the code will remain almost the same . Everything that can be done with quaternions, for example, interpolation and elimination of axis locking (Gimbal lock), can be done with rotors. But we begin to understand much more.
(In the original article, all the graphics are interactive, and the article is followed by a video. By clicking on the play buttons, you can launch the corresponding section of the video. You can also click the transition button below the video to go to the corresponding section of the article. You can maximize the window so that the video has more space , or set a constant size for it.)
1. Planes of turns
1.1. Turns are performed on two-dimensional planes.
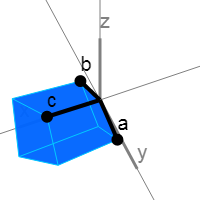
In three-dimensional space, we usually perceive turns as occurring around axes, as the wheel rotates on an axis, but instead it would be more correct to represent the plane on which the wheel lies. This plane is perpendicular to the axis.

This old woman spins the wheel in the plane. perpendicular to the axis .
This happens because if we divide the vector into two parts, one of which lies on the plane (), and the other is outside (), then the rotation rotates the inner part, while the outer one remains unchanged.

Rotate in the plane [ in the original article it’s an animation and the camera can be moved ]
In a two-dimensional space there is only one plane in which rotation is possible ( there is no outer part ). Therefore, it is strictly wrong to assume that turns occur around the third axis (perpendicular to the 2D plane), because we do not need to add another dimension to perform turns.
If you tell a two-dimensional “planter” (who lives inside a 2D plane and never gets out of two-dimensional space) about a perpendicular axis of rotation, then he would ask: “In what direction does this axis point? I can't imagine her! ”
Note
And in higher dimensions (4D and above) it is impossible to determine one vector of the normal to the 2D plane (for example, in 4D the 2D plane has two directions of normals, in 5D there are three directions of normals, and their )
1.2. The exact direction of turns
In addition, when we think about turning around an axis, the direction of turning is not defined, and therefore it should be determined by a rule (the so-called “right-hand rule”).
However, if we assume that turns occur inside planes, then the direction becomes clear: turn in the plane means a turn that moves a (unit) vector to (single) vector inside the plane that they together form. Rotate in the plane - this is a turn in the opposite direction: it moves the vector to vector .
Note
I remember that when I first learned about the three matrices of 3D turns along orthogonal planes, I first thought: what the hell is the matrix имеет противоположный знак? Так получается из-за правила правой руки, по которому мы должны определять поворот вокруг оси так, чтобы он выполнялся от к , а не от к , чтобы сохранять постоянное «праворукое» направление поворота. Когда мы начинаем говорить непосредственно о самой плоскости, это правило становится ненужным.
2. Bivektory
2.1. External product
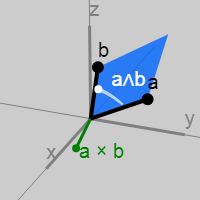
To calculate the rotation axis when turning one vector to another vector we take the vector product of two vectors to get a vector perpendicular to both of them. But why should we “leave” the plane if the turn is essentially a two-dimensional operation?
Instead, we take what is called an outer product (also known as a two-dimensional vector product) of two vectors, creating a new element called the “bivector” (or 2-vector)representing the plane that the two vectors together form. If the vector product creates a vector normal to the plane, then the external product creates the plane itself . Calculating the plane normal is irrelevant.
can be represented as a parallelogram constructed from vectors and in the plane that they together form.
At first, the idea of a bivector may seem strange, but soon we will see that they are almost as fundamental as the vectors themselves . If a vector can be compared with a straight line, then the bivector is similar to a plane ... The properties of the external product capture the important properties of the planes.
2.2. Basis for bivectors

Bivectors, like vectors, have components. But they are defined on the basis of planes , not straight lines , like vectors.
Three orthogonal basal planes are, and as we see from the figure.
But first, let's look at a simpler two-dimensional case ...
2.3. 2D bivectors
In 2D, there is only one plane, namely . That is, a two-dimensional bivector has only one component. For a bivector composed of vectors and this number equal to the area (with sign) of the parallelogram formed by two vectors.
In the original article with a 2D bivector, you can experiment on interactive graphics by changing the (single) vectors from which it is composed:
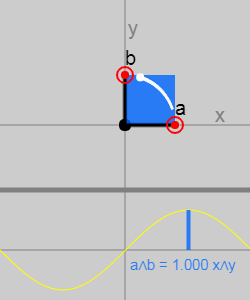
You can see that as the angle between the vectors changes, the area of the parallelogram changes (according to the sine of the angle).
If the vectors coincide or are parallel, then they do not form a regular plane and the result will be zero. This simple property defines what the bivector is:
Looking at the sum of two vectors, you can see that the property follows:
Consequently:
As well as the direction of rotation , the order of the arguments in the outer work is important. Reversing the arguments changes the sign of the result (this is called "antisymmetry").
On the chart, the sign is indicated by a color that changes from blue to green. Sign changes when turning out at moves from a clockwise motion to a counterclockwise motion (i.e. if it corresponds to a direction (from to ) or direction (from to )).
It can be seen that the properties of the outer work are arranged in such a way that they transmit the properties of the planes and turns.
2.4. 2D bivectors from non-unit vectors
Obviously, the vectors do not need to be of unit length, and on this graph, this restriction is removed:

The area of the parallelogram with the sign is proportional to the lengths of both vectors: where Is the angle between and . That is, for example, doubling the length of one vector doubles the area.
We can get the true value by substituting the vectors as components:
2.5. 3D bivectors

Same as vector coordinates can be considered as projections of the vector onto three orthogonal basis axes (, , ) bivector coordinates can be considered as projections smaller than a plane onto three orthogonal basal planes.
The projections of the vector are the lengths of this vector along each basis vector, and the projections of the bivector are the areas of the plane on each basis plane.
For a vector:
For the bivector:
Where , , - it's just numbers, like , , (they are underlined by colors corresponding to the colors on the chart).
The components of a 3D bivector are simply three 2D projections of the bivector on the basic 2D planes.
Using the same method as before, we find that the true values of the components look much like the XY component from the two-dimensional case, but applied to all three planes:
You can experiment with the 3D bivector on the interactive graphics in the original article:
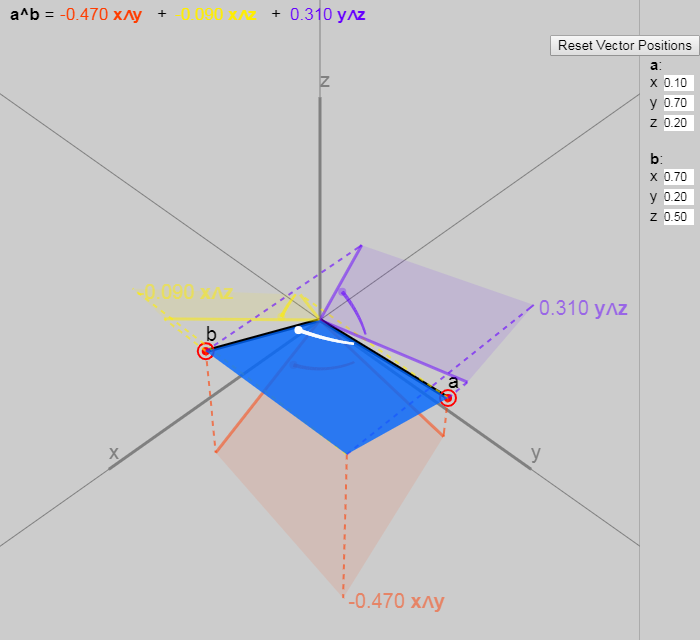
Note
Норма бивектора определяется аналогично норме вектора (квадратный корень из суммы квадратов компонентов). Это равно площади параллелограмма, образованного и , т.е. , где — угол между и .
If we divide a bivector by its norm, then we reduce two lengths of the vectors and the (absolute) value of the sine of the angle, that is, we will have a bivector. which will be constructed as if the two vectors were originally perpendicular and had a unit length. This is a very clean representation of the plane containing both vectors. So:
Do you recall anything external work? In 3D, the definition of an external work is very similar to the definition of a vector product. In fact, a vector in 3D, obtained from a vector product (for example, a normal vector) will have three components equal to the components of a bivector (the numbers will be the same, but the basis is different).
The definition of a bivector has a geometrical meaning, but does not appear from nowhere. I remember that when I studied vector art, I thought: “Why the hell does it return a vector whose length is equal to the area of the parallelogram formed by these two vectors? It seems so random. And why can we turn the area of a parallelogram into a vector length ? ”
2.6. The semantics of vectors and bivectors
In 3D, a bivector has three coordinates, one per plane: (, and ). Vectors also have three coordinates, one per axis (, and ). Each plane is perpendicular to one axis. This coincidence occurs only in three dimensions (*) and that is why we constantly confuse bivectors with vectors .
(*)
В 2D есть только один базисный бивектор (), а в 3D есть 3 базисных бивектора (, , ), в 4D есть 6 базисных бивектора (, , , , , ) и так далее...
In programming, they both have the same layout in memory, but different operations. Using a 3D vector instead of a 3D bivector is similar to the “type conversion” of a bivector.
Here is an example: you could see that normal vectors are transformed differently than ordinary vectors using the “inverse transfer” matrix, instead of the matrix itself. This happens because, in fact, they are actually not vectors, but bivectors, which have been transformed into vectors by “type conversion”. In physics, there is a hack called the “axial vector”, which was introduced in order to distinguish the vectors obtained by the vector product from the ordinary vectors. A bivector is a true “type” of an object and should be perceived and processed accordingly.
Trivectors
Мы можем продолжать брать внешнее произведение для получения не только ориентированных 2D-площадей, но и ориентированных 3D-объёмов. Тривектор можно получить, дважды выполнив внешнее произведение:
В трёхмерном пространстве всё на этом заканчивается. Как и в 2D, где есть только одна плоскость, заполняющая всё 2D-пространство, в 3D есть только один объём, заполняющий всё 3D-пространство.
[Но в nD мы можем продолжать создавать ещё большие внешние произведения векторов, пока не достигнем n-ного измерения. Например в 4D у нас есть четыре базисных тривектора (3-вектора) (, , , ) и один базисный 4-вектор ]
В 3D тривектор имеет только один базисный компонент (), равный объёму параллелепипеда, образованного тремя векторами. Тройное внешнее произведение является улучшенной версией скалярного тройного произведения (), потому что в нём задействован только один тип операций, оно возвращает корректный тип (объём вместо скаляра) и работает в любом количестве измерений.
3. Geometric product
3.1. Multiplication of vectors by each other
Geometric product (denoted without a symbol) is another operation that can be performed with vectors. The geometric product is defined so that the vectors have inverse values (for examplewhere 1 is just a number 1!) and have convenient properties, such as associativity (). The purpose of this is to be able to multiply the vectors so that (as is the case with matrices) the multiplication corresponds to the geometric operations.
Note
Наличие обратных величин полезно, потому что каким бы ни был объект , он не повлияет на векторы, то есть будет вести себя так же, как и при умножении числа на 1.
To determine the product, we first note that we can divide the product (or any function that takes two arguments) by the sum of the part that does not change if we change the arguments and the part that changes, as follows:
The first term no longer depends on the order of the arguments. and (it is called the “symmetric” part), and the second term changes its sign when changing the places of the arguments (it is called the “antisymmetric” part).
The scalar product of two vectors (also called the inner product) is symmetrical and is a measure of the distance (), so from a geometric point of view it seems useful that we make it equal to the symmetric part:
Similarly, the outer product of two vectors is antisymmetric, so it would be useful to equate it with the antisymmetric part:
In addition, the scalar product contains the cosine of the angle between two vectors (), while the outer product contains the sine of the angle. Together, they completely describe the angle between the vectors, as well as the plane they form.
Note
Именно полнота описания делает произведение обратимым, потому что мы можем перейти от одного вектора к другому с помощью информации, содержащейся в их произведении. Если я дам вам и , то вы сможете получить . Это невозможно сделать, зная только косинус или только синус/плоскость.
That is, the geometric product is:
This is strange because multiplying two vectors gives the sum of two different things: a scalar and a bivector. However, this is similar to how a complex number is the sum of a scalar and an “imaginary” number, so you could already get used to it. Here the part with bivector corresponds to the “imaginary” part of the complex number. Only this is not an “imaginary” value, it is just a bivector that we can truly show graphically!
In essence, multiplying two vectors, we calculate their useful properties ("the length of their projections onto each other" / "cosine of the angle" () and "the plane that they together form" / "sine of the angle" ()), which we put together a plus sign. The geometric product also gives the operations of “property groups” that can be applied to them, and these operations have geometric interpretations (for example: rotation and reflection of vectors). This we will soon see.
You can express a geometric product in terms of sine and cosine:where Is a bivector of both vectors on the plane, composed of two unit perpendicular vectors.
3.2. Multiplication table
The multiplication table allows us to make the product more specific: let's see what happens if we get the products of basis vectors (, , ).
For any basic vector, for example, the axis, the result will be equal to :
For any pair of basis vectors, for example, axes and The result will be the bivector that they together form:
(i.e. we can call simply , since this is the same thing!)
This gives us the following table:
In fact, this table is trivial compared to, for example, the quaternion table.
Note
Например, вот умножение двух векторов и :
3.3. Reflection formula (traditional look)

The reflection on the vector [in the original article, each vector can be moved]
If we have a single vector and vector we can reflect across the plane perpendicular .
This is done in the usual way: we share on the part perpendicular to the plane: , and the part parallel to the plane: .
Then, in order to reflect the vector, turn the perpendicular part, and leave the parallel part unchanged:
3.4. Formula for reflection (view for geometric work)
At this stage, we can replace the scalar product on its version as a geometric work and get the following:
(, because is a unit vector)
This gives us absolutely the same thing, but in another record. Using a record in the form of a simple work instead of a formula to encode such a fundamental operation as reflection will be very useful!
How multiple geometric product works
Если вы не понимаете, как работает многократное взятие геометрического произведения, то просто посмотрите на базисные векторы. Есть всего три возможных случая:
Результаты будут следующими: вектор, вектор, вектор + тривектор. Однако последний случай может возникнуть, только когда все три вектора независимы, что никогда не истинно для
Details
Любопытствующие могут посмотреть, на то, что происходит на каждом этапе с точки зрения геометрического произведения.
- Первый этап:
Если, как и раньше, мы разделим на часть, перпендикулярную к плоскости (), и часть, параллельную ей (), то мы получим:
, потому что эти векторы перпендикулярны, а , потому что эти векторы параллельны.
Первый член — это просто длина проекции на , т.е. первый член — это просто длина .
Давайте назовём нормализованной версией , то есть . Тогда второй член — это просто бивектор , умноженный на длину .
Этот бивектор составлен из двух перпендикулярных единичных векторов, то есть это очень чистое представление плоскости векторов и . Он не содержит информацию об их относительном угле или их длинах, только ориентацию плоскости.
То есть оба члена являются просто разложением на две ортогональные проекции ( и ), а также образуемой ими плоскость ():
Прежде чем переходить к следующему шагу, мы можем заменить внешнее произведение геометрическим, потому что и перпендикулярны, а потому их внешнее и геометрическое произведение будут эквивалентными (так так часть со скалярным произведением из их геометрического произведения равна нулю).- Второй этап будет следующим:
Первый член — это просто компонент вдоль , т.е. компонент , перпендикулярный плоскости. Другими словами, первый член — это просто .
Так как и (снова) перпендикулярны, их геометрическое произведение просто является их внешним произведением, то есть можно поменять их местами и изменить знак.- И наконец, последний этап переворачивает знак:
То есть мы видим, что компонент , перпендикулярный плоскости, перевёрнут, а параллельная часть остаётся такой же!
Note
Длина не очень важна, поэтому ниже мы её игнорируем, но если не является единичным вектором, то мы должны выполнить деление на его длину и формула превращается в , что больше походит на «послойное произведение», к которому вы уже должны были привыкнуть.
3.5. Two reflections are a turn: the situation in 2D
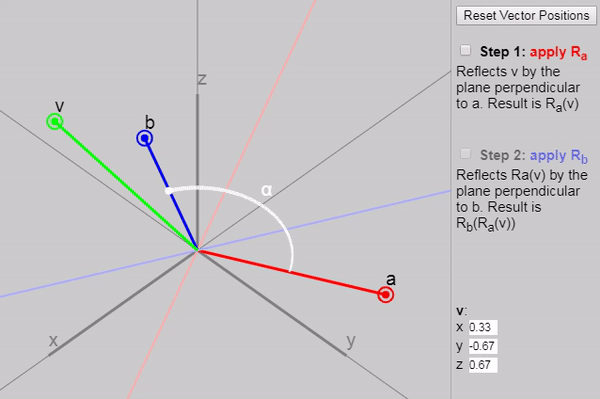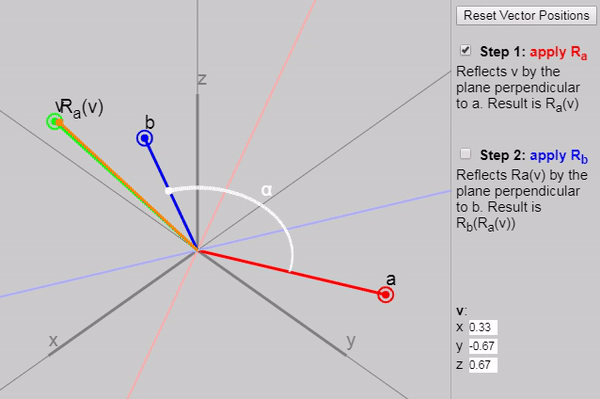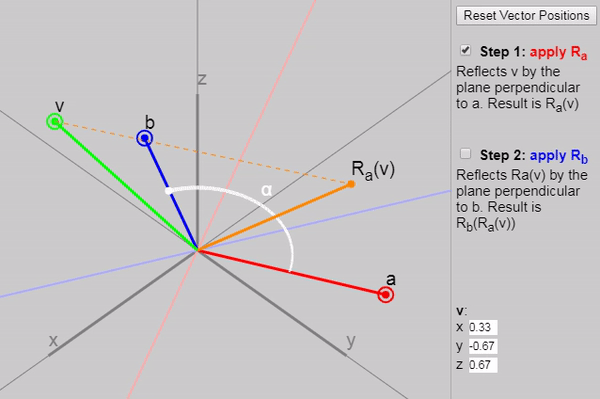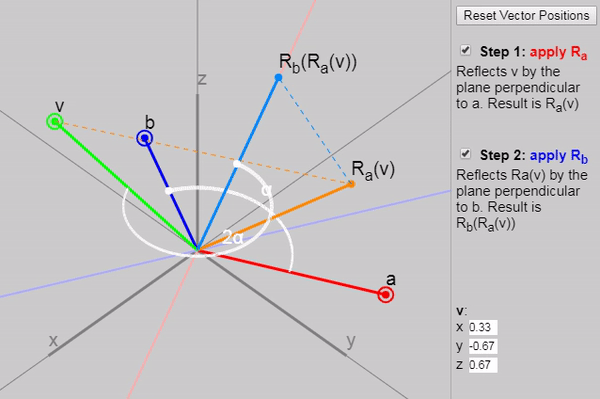
It turns out that if we apply to two consecutive reflections (first with a vector and then with the vector ), then we obtain a rotation by a double angle between the vectors and .
We can show each subsequent reflection stage in the graph below:
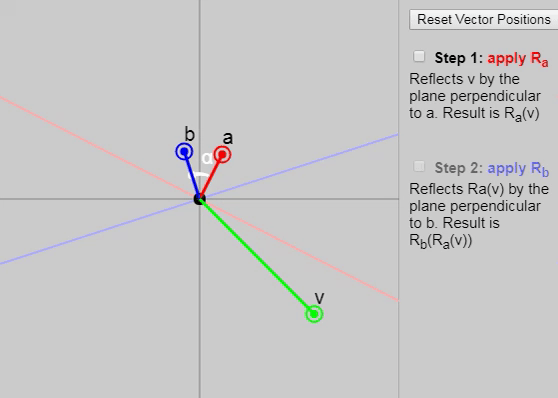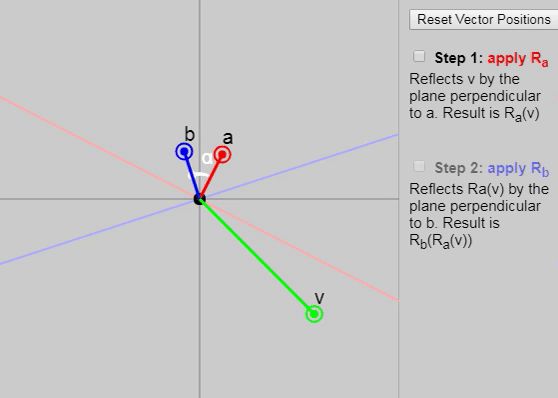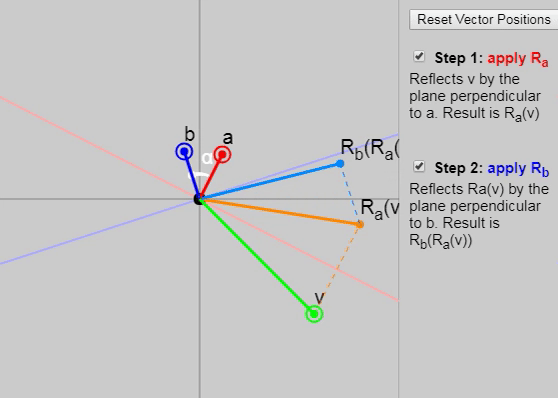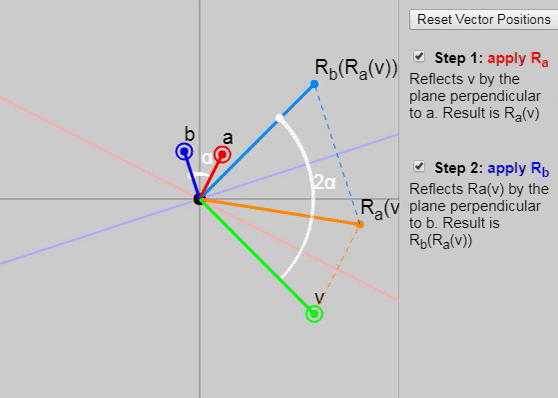
Also in the original article, you can change the vectors , and , but the initial configuration of the vectors on the graph (click on the “Reset Vector Positions” button) especially clearly demonstrates why the rotation results at a double angle. Another good configuration is the task as and axes and .
3.6. Two reflections are a turn: the situation in 3D
In the case of a 3D vector can be divided into two parts, one of which lies on the plane defined and and the other lies outside the plane (perpendicular to it). As shown in the graph below, when the vector is reflected by each of the planes, its outer part remains the same. As for the interior, we return to 2D, and it simply turns at a double angle!

3.7. Rotors
From a geometric point of view, the two reflections simply correspond to the following:
We call rotor because multiplying by on both sides of the vector, we are turning ( - this is the same as , only in the inverted part-bivektorom).
Rotor application to both sides of the vector turns this vector in the plane of the vectors and at double the angle between and .
And that is all!
Comparison of 3D rotors and quaternions
You can see that 3D-rotors in many ways look like quaternions:
In fact, the code / math is practically the same! The main difference is that, and replaced by , and , but they work basically the same way. Code comparison can be found here . I did not implement everything, for example, log / exp for interpolation, but they are quite simple to create.
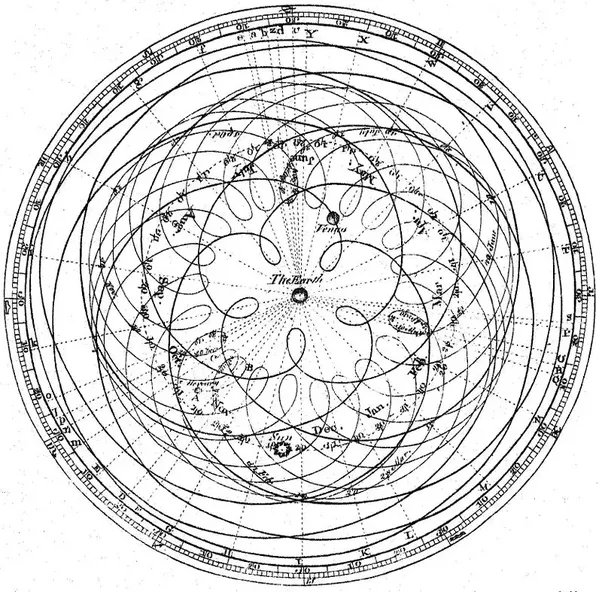
However, as we have seen, 3D-rotors are a three-dimensional concept that does not require the use of “four-dimensional double turns” or “stereographic projection” for visualization. Attempting to visualize quaternions operating in 4D to explain 3D turns is a bit like trying to understand the movement of the planets from a geocentric point of view. Those. this approach is too complicated because we look at it from the wrong point of view.
As we have seen, modeling turns as occurring inside planes, rather than around vectors, helps us a lot. For example, the squares of the basic bivectors give, just like basic quaternions ():
Multiplying two bivectors on each other gives the third bivector, but in fact it’s trivial, and we don’t need to remember that :
(Notice that we used )
These properties are a consequence of the geometric product, and do not appear out of nowhere!
Additional reading
(By the way, in geometric algebra there are not only rotors, but also other cool things!)
- Linear and Geometric Algebra by Macdonald [ link to Amazon ]
An excellent source, very clear and understandable, because it was meant that it will replace the textbook of linear algebra for students. - Geometric Algebra For Computer Science by Dorst et al. [ link to Amazon ]
Excellent source, because programming sometimes allows you to better understand the subject.Note: in this book, the authors make it clear that geometric algebra is slower than quaternions (and the like ...). In fact, it should have approximately the same code (i.e. you should not write code for geometric algebra, creating a generalized struct that can contain all possible types of k-vectors, just write one struct for each type of k-vectors if necessary That is, to replace quaternions, you can write one Bivector structure and one Rotor structure (which is Scalar + Bivector).