How to create reliable game mechanics using only Excel: modeling and optimization of solutions
- Transfer
We are searching, not iterating.
Basically, game design is a search process . Being engaged in design, we investigate a set of possible configurations of design for the solution of a specific design problem. For example, it can be a way to connect rooms in a dungeon, a set of functions and skills owned by various game agents, "magic numbers" that determine the effectiveness of units in the combat system, or the combination of possibilities that will be present in our game.
Just as a AI-controlled character uses a pathfinding system to move around the game world, the designer needs to navigate through the very high-level space of possible configurations, taking some initial configuration and iteratively changing it. We carefully consider a separate aspect of the design - the combat system, one of the parts of the game world, the technology tree in the strategy - and try to find a way to improve it by changing this configuration.
Designers like to use the term “iteration” to describe this process, but the word “search” would be more appropriate here. The truth is that when we create "iterations" of design, we experiment with the game we are developing. We make reasonable assumptions about small sets of modifications that turn the current configuration of the design into a new one, which, it seems to us, will better meet the design criteria.
Such “iterations” are completely unlike the linear changes that usually occur in the “iterations” of computer code; much more, they resemble a search in a maze with many sharp turns and forced returns back. Often they bring us closer to the goal, but it often turns out to be unclear whether the game has improved from them. Sometimes it turns out that design changes, which, in our opinion, should have improved the game, have unforeseen flaws and we need to roll them back or try again.
Game design is an incredibly difficult discipline. The design is like a dark room with a lot of sharp objects; It is extremely difficult to safely travel on it, moving away from the trodden roads. Almost always, painful injuries await us, especially if moving too fast. And we have quite a few tools to illuminate this dark room, as well as few clearly defined and detailed techniques for performing such a design search process.

Because of the existence of this dark room, we perform “iterations” - we do not know what the consequences of decisions will be until we check them. In other words, we are in search (Will Wright, in his report at GDC 2004, called it “search in the solution space”).
Therefore, very often, design becomes a bottleneck of performance, a major source of flaws and the biggest risk factor in game development. Countless number of development teams turned out to be hand and foot bound for ill-conceived design solutions, slippage in the creative process, changes in functionality, wrong perception of the target market and other design problems that led to product quality problems.
Taking into account all the dangers associated with experiments in design, it is not surprising that many publishers and major developers are so eager to avoid risk, preferring to strictly adhere to established and well-studied genres, licenses and genre assumptions. That is why they do not take on the well-known risks of innovation in design, which can bring unknown results. A study of a dark room is too risky.
We would like to find ways to change this attitude. Instead of just avoiding innovation, it’s better to find ways to improve our design skills, expand capabilities, and create powerful tools to make design innovations safer and more efficient.
This series of articles
This article will be the first in a series of posts about modeling solutions - a set of tools for decomposing solutions into formal models, which can then be used to search for the most desirable result.
Decision modeling and optimization are often used in management, finance, project planning, and many other areas to improve the decision-making process and solve various decision-making and optimization problems. This is accomplished by searching among possible alternatives, which is faster than manual choices made by people.
Despite all its potential advantages, modeling and optimization of solutions seems to be a rather unexplored topic for designers in the gaming industry. A survey of professional designers at a popular developer forum showed that only 25% of respondents had at least heard about decision modeling, and only 8% used it in practice. A similar survey conducted among designers via Facebook showed about the same results with a similar number of respondents.

When used properly, solution modeling can significantly improve many aspects of the design process:
- It can help to optimize the configuration of specific design systems or the optimal values of game parameters.
- It can shed light on solutions as a combination of features that need to be included in the game.
- It helps to simulate the decisions that a player can make, in particular, to identify the dominant strategies or ways in which the player is able to "beat the system."
In this series of articles I will talk about examples from all three categories of use.
Definition
What is “decision modeling”?
Simply put, then:
Solution modeling is the process of simulating a solution with the subsequent automation of the search for its calculation.
We start by specifying a solution, then we try to select all the factors of which this solution consists, and then embed them into a model that accurately describes the solution, and specify a set of input variables and one output variable. Then we search for optimal solutions for a set of solution variables (or incoming variables) that create the best output from all possible.
If everything is done correctly, then we will be able to search for a much larger number of possible solutions than it would have been done manually or in imagination. Although we cannot apply this system to everything, for some tasks we can get better results, calculate them faster, and in some cases we can even solve problems that cannot besolve in no other way.
During this process, we also specify a set of one or more conditions that are used as boundaries that support the validity of our model. Such conditions may limit the range of values or the type of incoming variables, as well as any other aspects of our model.
Why build models?
If you played Sid Meier's Civilization , then you probably wondered sometime: “Wait, how is the most correct way to start developing the city? Do I need to first build a monument, and then a warehouse? Or do you need a warehouse first? And maybe first the temple, and then the warehouse? What is the best decision to take? Can I even answer this question? ”
You can also recall the mechanics of battle in real-time strategy. Balancing the parameters of multiple units in the RTS is a task notorious for its complexity. What if we had a system that allows us to speed up the solution to the problem of balancing, answering questions about balancing the battle of the game without playingtesting each solution? What if we could ask the system questions? For example: “How many swordsmen do you need to defeat two pikemen and three archers?” Or: “what is the cheapest combination of archers and catapults that can defeat an enemy watchtower?”
In fact, such a system can be created!
If we manage to model these design problems in the right way, then we can use automatic optimization tools to search through all possible answers to find the one that best meets our criteria, without having to play the game thousands of times.
Here is an example of a similar task — an example that we will solve in a future article in the series.
Let's say we have a game called SuperTank. In SuperTank, we control a huge, fantastic tank, fighting on the battlefield with other supertanks. Before each battle, we can choose a certain combination of weapons for our tank.

We have 100 credits that can be spent on equipment. A player’s supertank can carry 50 tons of weapons, and also has 3 “critical” slots for special high-power weapons.
The game has the following five types of weapons, and the player can use any number of each type, or completely abandon it:
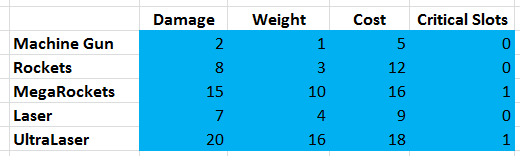
Suppose we need supertank to have the highest possible damage value (we assume that damage per second is specified, regardless of the weapon’s firing speed). Also assume that all weapons have the same range, projectile trajectory, accuracy and frequency of fire, that is, they are identical in everything except the values shown in the table.
Now quickly answer how many machine guns, rockets, lasers, etc. need to be placed on a supertanka? Which combination of one or more weapons will give us the most damage, without exceeding the limits of weight, price and critical slots?
Try to solve the problem manually or using a calculator.
Can this be done?
If you try, then quickly make sure that this is a surprisingly difficult task.
Perhaps there is a way to solve it using complex mathematical equations, but we are designers, and mathematics is not our fad.
Think also about how the answer will change for other parameters. Will the answer change if instead of 50 tons supertank can hold 60? Or if instead of 100 credits we will have 110 or 90? How to change the optimal equipment? And if we have 2 or 4 critical slots?
Now imagine that we have a system that instantly calculates the weapon placement pattern with the highest damage for any set of parameters (Weight, Price, Critical Slots). It is enough to enter the parameters of the weapon from the table, then enter the parameters of the supertank (50 tons, 100 credits, 3 critical slots) - and BOOM! - we got the best gear.
Wouldn't that be wonderful?
We could use this system to instantly receive an answer to all sorts of useful questions:
- How will the optimal scheme change when changing the parameters of supertank?
- How to change the optimal equipment when changing the parameters of the weapon?
- What is the maximum damage can cause supertank with any given parameters (Weight, Price, Critical Slots)?
- Are all four weapon parameters (Damage, Weight, Price, Critical Slots) appropriate and balanced for each type of weapon?
- Do we have too powerful guns that are used too often? If a weapon is so useful that it is always the right way to use it, then it will always be the best solution, so there will be no meaningful choice here. In this case, we should either remove the weapon from the game, or change its balance so that in certain conditions it is not useful.
- Do we have rarely or never used weapons? Similar to the previous paragraph - if a type of weapon is so useless that the right decision is never to use it, then there is no meaningful choice either. In this case, it is worth either to remove the weapon from the game, or to change its balance, so that under certain conditions it would be wise to use it.
These are all very important design questions that any designer should want to know. Knowing these answers will be incredibly useful when balancing the game SuperTank .
In just a few paragraphs, we described a task that is very difficult for us to solve manually, but which is trivially solved using the tools built into Microsoft Excel.
In a future article, we will build a real decision model for this example that will answer all the questions listed.
You will see that a model that can be created in minutes will allow you to solve this complex task. In just a short time we will create a powerful tool that allows us to quickly and reliably explore the design space.
Road map
In this series of articles, we will illustrate a few more complex examples, and create reference spreadsheets so that you can run all these examples yourself, from the tools having only installed Excel. Among these examples will be the following:
- A simple example of combat for a strategic game.
- A model for optimizing the coordinates of several wormhole teleports in relation to each other and populated sectors in a massively multiplayer space game (MMO)
- The model that determines the level of taxes for a simplified model of the city, to balance the satisfaction of residents and tax revenues in 4X-strategies like Sid Meier's Civilization
- The spell and skill selection model for character classes in a massively multiplayer game
- Optimization model for determining the optimal order for the construction of a planetary colony in 4X strategies like the classic Master of Orion
- An example of a team trying to choose the right combination of features for the game, and a decision model that helps them choose the appropriate tradeoffs
In general, this series will be made up of simple examples of finding the optimal strategies of a player in specific subsystems of the game, and then proceed to decision models that allow optimizing the parameters of gaming systems and optimizing combinations of feature sets.
In each of these cases, we describe the problem, show how to model it in Excel and solve it using the built-in Solver tool (in the Russian version - “Finding solutions”) from Excel. In each case, you will see that we can make it easier, faster and more reliable than without using Solver or a similar tool. Also for each example I’ll add spreadsheets so you can download and check them yourself, recreate the results and experiment with your own models.
Also, do not forget that the internal representation — whether it is a spreadsheet, a program in a high-level language, or something else — does not matter . What is important is not what we work in - in Excel and Solver, Java / C ++ / C #, or in something else, but the fact that we are modeling the task and we are trying to solve it.
Why use solution models?
Some readers may be skeptical now. It seems that building models of solutions requires a lot of effort. Why do we need all these efforts if we can conduct user testing in the form of focus group testing and beta testing?
To begin, I will say that decision modeling does not apply to every task . Some tasks are too complex or too difficult to model using such techniques, and there are many aspects to the design (for example, aesthetic considerations, the value of the game as entertainment and the “feel” of the game) that are difficult or even impossible to model numerically. And modeling solutions are definitely noteliminates the need for group testing, beta testing or daily play in your own project during its development.
But even with all this in mind, by the end of the series of articles it will become clear to you that the methods of modeling and optimizing solutions give us a unique and powerful set of tools. They can completely or partially solve many problems that cannot be solved in any other way, as well as provide you with answers and information about all sorts of design issues that are difficult to obtain in another way.
As in the case of any other tool, its user must make a decision about its applicability.
There are many cases where decision models may be unacceptable or too cumbersome. But as you will see in the series of articles, they are also surprisingly useful, and the more we make the right design decisions and get rid of bugs in the early stages, even before the testing stage, the greater the likelihood that the design systems will be strong, fascinating and infallible.
Think about the tools available to a typical programmer. The work of programmers is very complex, but it is simplified by many tools that help find bugs even before the testing phase. They have compilers that constantly remind you of typos; they have defensive programming practices that detect software defects; they conduct a review of the code, which helps to recognize flaws in another's code or point out perverse programming practices; In addition, they have a lot of profiling and static analysis tools that allow you to get rid of all sorts of performance bugs and other defects.
But designers have no such tools. We can say that our work is just as complicated, but we do not have a compiler that would tell us that we “made a syntax error”. We do not have a profiler, debugging tools, or static analysis tools. We cannot review the code, because we have no “code”. We write specifications and design documents, and that’s it; we can share diz-docks and feature specifications within the team and hope that colleagues will give us good feedback, but more often we need to put the system into the game to see if it works or not.
This makes the design an incredibly risky, long and costly exercise.
As is the case with programming, people tend to make mistakes and this is an integral part of the process, so we needas many high-quality tools as possible to protect yourself and your projects.
We are still very far from having complete design tools to help designers explore the design space. We still need to go the way compilers, debuggers, profilers and static analysis tools in programming have done. But we are already seeing the dawn of several specific solver and game design tools, including the Play the Tester version of Cut the Rope called Cut the Rope: Play Forever ( link ); the abstract Ludi game design system that generated the board game Yavalath ( link ); and my own automated assistant Evolver for balancing the mobile game City Conquest ( link).
Modeling solutions will help us take a few more steps to this level of support and will allow us to begin to complement and expand the designers' own intelligence with the help of automated tools. And if we have a choice: to have or not to have the tools, why choose “not to have”?
The main thing is not spreadsheets, the main thing is models
This series of articles is written for designers - that is, for all designers, regardless of what experience they have: artistic, software, experience creating storytelling or board games. Therefore, we will not complicate and promise the following:
- No code . There will be absolutely no code in the articles and we will illustrate all the examples in Microsoft Excel with the help of the built-in Solver tool (“Solver”). However, it is important to note that this series is not about spreadsheets or Excel, but about modeling and optimization of solutions. Each step we take in this series can be just as easily (and sometimes even easier) done in any high-level language.
- No mathematics (or at least nothing complicated). We strive to make this series free of mathematics and will not use anything other than the simplest arithmetic operations: addition, subtraction, multiplication, division, and sometimes calculating the square root. Greek letters will be strictly prohibited.
- No four-dimensional spreadsheets ; we will use only two-dimensional.
If you are a designer, then this series of articles will give you all the tools you need to create solution models yourself, without the need for you or programmers to write code. If you are a programmer, then the series will give you a fairly straightforward instruction on programming your own decision models on any HED, so that you can build your own decision models, either from scratch, or based on a template that is already used in Solver and in Excel.
These articles should be just a starting point, so you can take the concepts presented here and choose yourself: whether to implement them in Excel, whether to choose another optimization tool, or try to build your own solver in a high level language. Spreadsheets are a solid foundation to begin with, but such solution models are likely to become just your springboard to richer and more complex models that integrate into your game architecture.
Explanations
Before we get too far in modeling solutions, we need to give some explanation. Modeling and optimization of solutions do not create any complete system for game design, and we will not say anything like that. It is useful to look at them as a tool that helps in some aspects of the design process, and as any tool, it has many limitations.
Here are some of the limitations you need to know about:
- They are easy to use incorrectly. Like any other tool, decision models can be used incorrectly or in an inappropriate way, and an incomplete or erroneous decision model can lead you to the wrong conclusions. As in the case of software, the larger the decision model becomes, the greater the likelihood of errors in it. In addition, it is very easy to mistakenly interpret what the model tells you, or to build an incomplete model that does not accurately model the decision that you need to make.
- They are complex (sometimes). Some design tasks are too complex to be modeled with this approach. In many tasks, there are too many “moving parts”, or they are too tightly integrated with other aspects of the game, so that they can be qualitatively presented as a separate Excel spreadsheet. In such cases, it is necessary to make a decision either to model only a part of the system (which may result in an incorrect / inaccurate model), or on the integration of the full model into the game itself (which may require a lot of effort), or to completely abandon the simulation.
- You can not model everything . Solution models cannot tell you whether something will be fun, aesthetically pleasing, “right” or giving the user a convenient and accessible interface. There is no general way of representing such subjective and aesthetic aspects in the form of a discrete model. This means that there are clear limits to the use of modeling solutions, and that they are much more useful for the design of systems and optimization of mechanics / dynamics than for aesthetics.
- They have limitations . All optimizers have their limitations, including the Excel Solver used by us, and it is possible to create solution models that have the right solutions, but are so complex that no optimization tool can find them. In the case of sufficiently large unlimited input values, the task may outgrow Solver’s ability to search for each possible combination of input values, and instead it will have to rely on various optimization methods. As we will see in this series of articles, it is possible to simplify the expressions of the models so that the “Search for solutions” makes it easier to process them. Developer Solver ( Frontline ) offers a more powerful solver for more voluminous tasks, but you can definitely create models that Solver cannot solve.
- They do not guarantee optimality . Due to the fact that we work with complex models, it is impossible to be 100% sure that we have found the optimal solution. Sometimes we have to stop at the second best: we will spend more time on optimization or start from scratch and re-optimize so that we can say with a high degree of confidence that we have found either the optimal or very close to the optimal solution.
Last and most important:
- We need to make sure that the model is engaged in the right tasks . Not all tasks are important enough that such efforts are required, we need to know our priorities exactly and avoid unnecessary focus on optimizing useless tasks and ignoring other, larger ones, which may turn out to be much more important.
To put it simply, in order for solution modeling to be useful, certain conditions must be satisfied. We should be able to embed the solution in question in a certain discrete model, and express the result of the solution in the form of a single value. In other words, we must be able to express a finite set of incoming data in a single output value using a decision model in such a way that minimizing or maximizing the output value gives us an improved solution.
In cases where there are subjective aspects that cannot be built into this model, for example, aesthetic aspects or usability / playability aspects, we will need to either clearly separate them from the decision model, or use decision modeling as a first pass, or simply completely abandon decision modeling .
In order for us to model solutions in a spreadsheet, we must also limit the complexity of the model. If our game does something very complicated, we may not be able to recreate this complexity in Excel. However, it is necessary to take into account that this restriction is only the power of the models that can be built in Excel, and not the models of the solutions themselves. In our own game engine, we can build much more powerful solvers, and I hope that this series of articles will inspire you to do just that.
On the other hand, all these restrictions are unlikely to make decision modeling useless. Even in the case when the task is too complicated for full optimization in the model of solutions, this model can still help us to find a lot of design components that are much closer to the correct configuration, and also to find and debug many basic tasks in the early stages of development.
And even when the decision model cannot find the optimal solution to the problem, either because the task is too complex, or because it requires an aesthetic approach and other subjective human factors, it can still help narrow the boundaries of the solution, allowing you to eliminate dead ends and otherwise reduce the complexity of the problem .
Finally, even if you decide not to use modeling solutions, not to try to optimize spreadsheets, or create your own solvers, understanding modeling solutions will still help you change the way you look at design decisions.
This series of articles is a study. We will look at many examples of game design problems and explore ways to model and optimize them, provided us with powerful design tools. You may be skeptical or decide not to use optimization at all, but I hope that you will follow our research and find out how we will complete the series.
Conclusion
In the end, we want to create the design correctly .
Many design questions are subjective, they have no “right” or “wrong” answers. But in some cases, they certainly are . And in such cases, we must know how to get the right answer, or at least understand how to take up the definition of the “right” answer and look for whether there is a solution.
Solution modeling and optimization are powerful tools that help us in many cases. I believe that such tools should be in the toolkit of each designer. By adapting to them, you will realize that these tools have a huge untapped potential in a more rapid and reliable study of the dark room of game design. In our series of articles, we will show how many uses it has.
Part 2. Basics of Optimization and Deployment Simulation
The spreadsheet for this article can be downloaded here .
Preparation of a decision model
Now that we have talked about decision models, explained how they are useful and listed some of their limitations, we would like to illustrate the basic concepts with a simple example.
But before we do this, you need to introduce some rules regarding the structure and format. As in the case of the code, if you do not be careful, spreadsheets can quickly turn into chaos.
To put it simply, there will be four types of cells in our spreadsheets:
- Solution - these cells contain variables that we are trying to optimize - in other words, we will force the optimizer to try to find the best values for these cells. In these cells, we can start with 0 or some other acceptable default value, and then force the optimizer to insert the correct values. In most cases, we will also limit them to a certain interval, for example, the minimum and maximum values, and in some cases, integer or binary values. For the sake of consistency and readability, the decision cells will always be yellow and have a black border.
- “Set value” - the values of these cells are specified directly in the task conditions. For example, if the task tells us that the Tootsie Pop lollipop weighs 17 grams and each time we lick 0.25 grams from it, then these two cells will be “given values”. We denote such cells by blue.
- "Calculation" - the values of these cells are calculated from other cells in the spreadsheet that do not fall into any other categories. We will make them gray.
- “Target” (or “output”) is a cell whose value we seek to minimize (or maximize) when executing the optimizer. In our examples there will always be only one target cell, it always has an orange color and a black outline. ( Note: there are more powerful solvers that support working with several goals, but for our articles it will be too difficult.)
When we run the optimizer (Solver tool (“Finding solutions”) built into Microsoft Excel), it will simply look at the target cell we have indicated, and then try to change the decision variables, but it can (within the limits we set) either minimize or maximize the value of this target cell (whatever we specify).
Solver knows almost nothing about the calculations that take place inside, or about the connections between decision cells and target cells; he simply performs one of several algorithms available to him, trying to minimize or maximize the value of the target cell by searching for possible values of the decision cells. Such algorithms ("Simplex LP", "GRG Nonlinear", "Evolutionary") are designed so that they are much smarter than exploring all possible variants of variable solutions by brute force search, and very often find answers to serious problems with surprising efficiency.
For example, if we wanted to know how many times you need to lick to get to the middle of Tootsie Pop, you could use a similar spreadsheet:

We can ask Excel Solver to solve this problem by ordering it to minimize the target mass “Mass remaining on Tootsie Pop” (“the remaining mass of Tootsie Pop”), and he would quickly determine with the help of experiments that the value of the yellow solution cell that gives this result ( “How many times to lick to get to the middle of Tootsie Pop”) is 68.
Of course, it’s a little silly to do that, because from the statement of the problem it is clear that the answer will be 17 / 0.25 = 68. It makes no sense to run the optimizer to solve a problem that can be solved by simple arithmetic.
However, in practice, most of the problems we face will not have simple mathematical solutions. They will have a lot of decision variables that lead to the goal in unobvious ways, and comparing decision variables and inference will be too complicated an operation for calculating a mathematical equation manually (and I repeat that in this series we will carefully avoid complex mathematics).
We will focus on describing the tasks, and leave Solver to complete the difficult work.
Example 1: Taxes
In our first real decision model, we show an example of determining the optimal tax rate. Nobody likes taxes, but in this case we will not pay, but receive taxes; I hope this will reduce your torment.
Imagine that we are creating a 4X strategy similar to Sid Meier's Civilization . We are in the process of creating cities that have a certain level of discontent, depending on their size. “Dissatisfied” residents are essentially not committed to cooperation, and we do not receive income from them. We can also try to get money from cities by changing the tax rate of each city, but if the tax rate increases, the level of dissatisfaction will increase exponentially, so very high taxes become counterproductive.
Suppose also that we can specify a tax rate with an increment of 10% in the range of values from 0% to 50%. Here is a screenshot showing a similar system from the classic Master of Orion 2 4X strategy :
As designers, we want to ask a simple question: what will be the optimal tax rate in the general case?
This should be a simple task, because there are only 6 acceptable values of the tax rate. We can simply test each of the 6 values manually, find the one that gives us the most revenue, and at that consider the problem solved!
(In fact, you can probably find a mathematical equation to solve this problem, as in the Tootsie Pop example, but this will be counterproductive because we are preparing this model to grow into a more complex one that cannot be solved using In addition, in this series of articles we avoid mathematics.)
Let's start by describing the problem as follows:
- We have a city of 12 (which means 12 million people). These people are represented as 12 separate "citizens".
- Every citizen at any time can be pleased or displeased.
- Satisfied citizens pay in the form of taxes (tax rate x 10) (that is, for example, a tax rate of 20% gives us 2 units of currency in tax revenues for every satisfied citizen).
- Dissatisfied citizens do not pay taxes.
- In the city there are 3 dissatisfied citizens who remain dissatisfied, regardless of the tax rate.
- An additional number of citizens become dissatisfied based on the following formula: (Population) x ((Tax rate) x (Tax rate)) x 3.5, the value is rounded down to the nearest whole number. For our city of size 12, this will give us 0 additional dissatisfied citizens at the rates of 0% and 10%, 1 additional dissatisfied citizen at the rate of 20%, 3 additional dissatisfied citizens at the rate of 30%, 6 at the rate of 40%, and 10 at rate of 50%.
It's simple, right?
We describe this in the spreadsheet attached to the article as follows:

You may notice that we set the yellow cell of the solution (Tax Level (0-5)) as an indirect way of specifying the tax rate. Instead of specifying the tax rate directly in the solution cell, the Tax Rate calculation cell takes the Tax Level number from the solution cell and multiplies it by 10%. There is a logical reason for doing this indirectly, and we will see soon.
Now we can experiment and substitute all possible values of the level of taxes. You can simply enter each of the digits from 0 to 5 into the Tax Level cell and get the following:
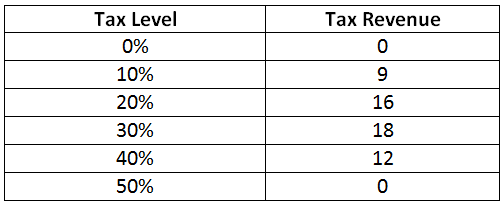
As you can see, there is an optimal tax rate: 30%, which maximizes tax revenue, giving 18 units of currency.
Let's automate the system!
This is great, but what if we have more than six options? What if there are hundreds of possible tax rates, or will we need to change other decision variables? Everything will become too difficult to test values manually.
As we shall see, it is precisely for this that Solver is used.
To begin with, we reset the Tax Level cell to zero. Then go to the Data tab ("Data") Excel and see in the right part of the ribbon, in the Analysis section, the Solver button ("Search for a solution").

If you do not see it, go to Options (“Options”) Excel, select the category Add-Ins (“Add-ins”), make sure that Excel Add-Ins is selected in the Manage drop-down list (“Excel Add-ins”) ), click Go and make sure the Solver Add-in box is checked.
After clicking on the Solver button, you should see a similar dialog box.

Let's now look at all the steps involved in setting up a Solver dialog box.
In the “Set Objective” field (“Optimize Target Function”) we will indicate what needs to be optimized. In this case, we are trying to get as much tax revenue as possible, so we’ll select the orange target cell, which denotes tax revenue, and then click on “To: Max” in the list of radio buttons.
In the “By Changing Variable Cells” section, select the cells that “Search for Solutions” should calculate. We need to determine the optimal tax rate, so we choose the yellow cell of the solution (Tax Level (0-5)). If everything works out correctly, as a result, this cell will be assigned a value of 3, corresponding to a tax rate of 30%, the optimality of which we have already determined during manual calculations.
Finally, we need to add a few restrictions . In essence, constraints are conditions for any cells of our solution model, and Excel Solver will focus only on those solutions that satisfy the specified constraints. Such constraints can limit certain cells (usually decision cells and computation cells) to specified minimum and / or maximum values, and / or force Solver to process them as integer or binary variables (0 or 1). Constraints are incredibly useful for creating the correct model, which will be limited.
Solver requires at least a few constraints that allow it to determine the boundaries of the decision cells — in other words, the minimum and maximum values for each cell. To add a restriction, you need to click on the Add button on the right, after which the following dialog box will open:
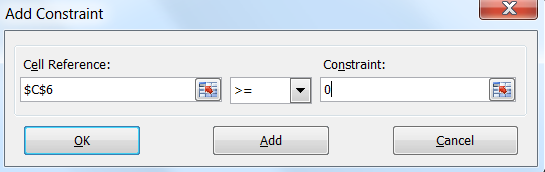
We will add two restrictions, one for the Tax Level solution cell to satisfy the condition> = 0, and one more for the solution cell to be <= 5. Then, in the Solving Method list (“Choose solution method”), select the Evolutionary value (“Evolutionary search for a solution ") and click on Solve (" Find a solution ").
After working for about 30 seconds, Solver will give us a similar answer:

Oops, there was a problem. Solver received the correct amount of income, but the tax level is wrong. A player can set taxes only with an increment of 10%, but Solver obviously sets fractional tax rates, which the player cannot do.
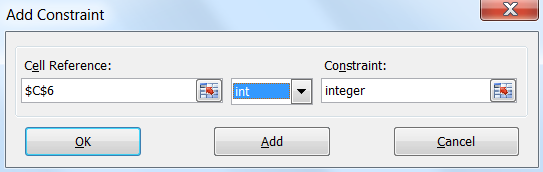
You can solve the problem by limiting the value of the tax rate cell to whole numbers only. It can only be 0, 1, 2, 3, 4, or 5, but without intermediate values.
Fortunately, Solver can do this quite easily. Open Solver, click the Add button, select the Tax Level solution cell, and then select an int limit from the middle drop-down list:
Now run Solver again and get the following:

Perfect! With a little effort, we got the right answer in Solver. As we will soon see, with an increase in the scale of tasks, the volume of work performed for us by the instrument considerably exceeds the time spent on its setup.
Growing city
Let's now expand the task, slightly complicating the model of the city.
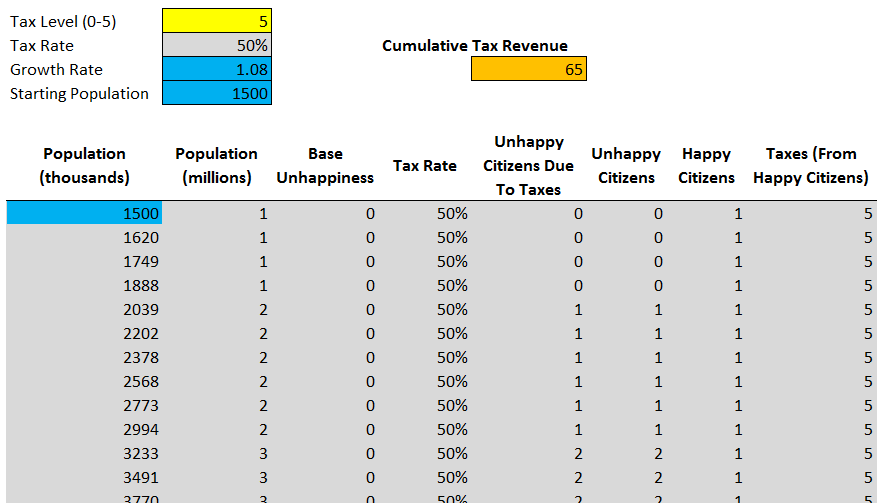
In any 4X city strategy (or planets, or colonies, or other inhabited units) grow over time. We assume that the city has a constant increase of 8% per turn, starting with 1,500 thousand (1.5 million) citizens, and increasing to the size of 12 million inhabitants. Now our spreadsheet will look like this:

Each new subsequent line of the table describes one turn of the game.
We also changed the calculation of the basic level of discontent. Now it is calculated as one second of the basic level of the population (in millions), rounded down. Due to this, basic discontent will be equal to 0, until the city grows to size 4, after which it will grow linearly with increasing size of the city.
As before, we can experiment with tax levels manually, changing the Tax Level values. We will receive 0, 102, 190, 222, 144 and 65 units of currency in tax revenues, with each tax level from 0% to 50%.
And we can again force Solver to solve this problem; he will quickly determine that the optimal tax rate is 30% as before, which gives us an income of 222 units of currency. Here’s what the Solver dialog box looks like:

Variable tax rates
But, of course, the player will not play that way. Our simulated "city" sets one tax rate and keeps it the same for each turn of the game. But a real player can have a tax rate at any time, and he will often need to set it up because his city is growing and circumstances change.
Wouldn't it be great if we can not just determine a single optimal tax rate, but also calculate the optimal value in each turn?
She will instantly tell us how the player can best adjust the taxes.
And it turns out that this can be done! Already setting the decision model in the right way, we can make it incredibly simple.
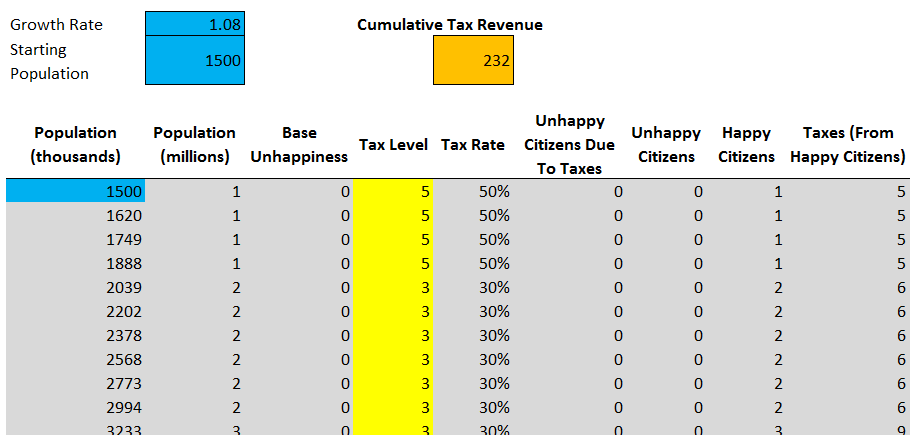
The biggest difference is that we need to remove the Tax Level (0-5) solution cell and replace it with a whole column of tax level cells, as shown below.
Now instead of forcing Solver to optimize a single cell, we’ll order it to optimize the entire Tax Level column. This is how the Solver dialog box will look like - you can see that it is almost the same as before, but instead of a single cell, the variables and constraints now represent a whole range of cells in the Tax Level column.
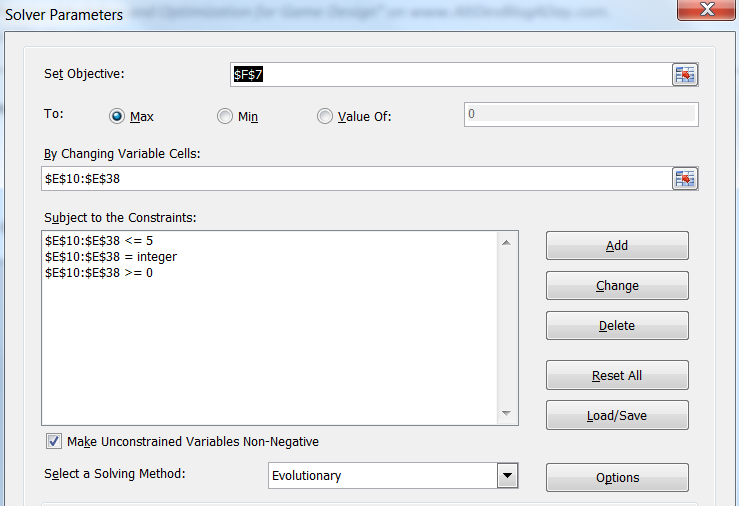
Solver indeed proves that changing the tax rate changes the results - the cumulative income now amounted to 232 units of currency. Compared to the same tax rate, growth is only 5% per cent (222 against 232 units), but it is still significant, because we know that some players will be able to achieve it.
Looking closer to the Solver solution, you can see that it starts with a tax rate of 50%, because the city of size 1 does not contain enough people to generate dissatisfaction. In the process of city growth, the instrument changes the tax rate in each move in the range from 20% to 30%, depending on which of them brings a greater income.
The spreadsheet for this example can be downloaded here.; in it, the three stages of this example are divided into separate sheets of a spreadsheet (the same tax for a city with a permanent population, the same tax for a growing city, and a variable tax rate for a growing city).
Conclusion
The solution we found shows something interesting: the discrete nature of our game simulator, representing the arbitrary grouping of millions of people as discrete “citizens” who may have one or two discrete states of contentment, introduces characteristic features into the model. Although the game itself at some level will require such discretization for the sake of accessibility and playability, smart and cunning players will be able to exploit this artificial fractionality to gain advantages over players who do not want to bother with the levels of taxes in each turn.
This situation leads to an interesting question: do we want this? Does the mechanics make the players assume that for the game they need to do micromanagement of tax levels at every turn? And do we want to allow the winning players (power gamers) to beat the system in this way; Does such a trick match the gain of 5%?
These questions I can not answer. In the end, you are a designer who sets design goals, so it’s up to you whether this level of system operation is in line with the goals you set for the game.
Of course, this model is just a bare frame. In a real 4X strategy, players can make all sorts of decisions about how to develop a city, build buildings, and make other changes that affect the growth of a city, contentment, tax revenues, and productivity.
In one of the future articles of the cycle, we will build a similar, but much more complex model of an entire planetary colony in a game resembling Master of Orion 2 . This example will be much more sophisticated, because we will be able to make decisions in each move, which will further affect all these parameters, such as growth and productivity, that is, each decision will have consequences that affect subsequent decisions. However, we still see that the Solver evolutionary tool optimizer is able to cope with this task.
In the next article, we will fulfill our promise and optimize the purchase of weapons for SuperTank in the example from the introductory article.
