Starting from version 8.2, the Intel Performance Primitives (IPP) library systematically transfers from internal parallelization of functions to external. The reasons for this decision are outlined in the article IPP Functions with Border Support for Image Processing in Multiple Streams .

In this post, we will consider the functions that implement the filter with the final response - the FIR filter (Finite Impulse Response).

FIR filter

Filters are one of the most important areas in digital signal processing. And, of course, the IPP library has the implementation of most classes of these filters, including the FIR (finite impulse response) filter. A detailed description of FIR filters can be found in numerous literature or on Wikipedia, but if briefly, in a few words, then the FIR filter simply multiplies several previous samples and the current sample of the input discrete signal by the corresponding coefficients, adds these products and receives the current sample of the output signal. Or a little more formally: the FIR filter converts the input vector X of length N samples into the output vector Y of length also N samples by multiplying Ksamples of the input vector to the corresponding K coefficients H and subsequent summation. The number of coefficients K is called the order of the filter.


Fig. 1. FIR filter

Here:
tapsLen is the order of the filter,
numIters is the length of the vector.
The figure is taken from the documentation for the IPP library, therefore, the terminology accepted in IPP is used.
Visually, you can imagine the FIR filter as follows.


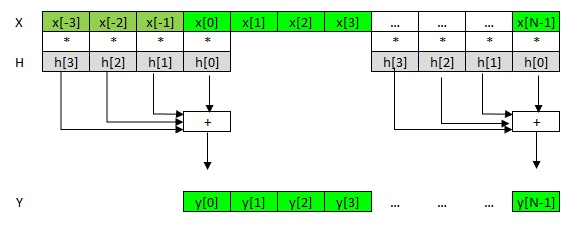
Fig. 2. FIR filter schematically

As you can see, here the filter order K is 4 and we simply multiply the 4 filter coefficients h by 4 samples of the vector x, add and write the sum in one sample of the output vector y. Note that the filter coefficients h [3], h [2], h [1], h [0] are in the memory in the reverse order with respect to x and y, in accordance with the generally accepted formula in Fig. one

Delay line

Since the FIR filter is an ordinary convolution, to obtain an output vector with a length of N samples, N + K-1 input samples are required, where K is the length of the core. The first K-1 samples will be called the “delay line” (delay line). In fig. 2 they are numbered x [-3], x [-2], x [-1]. The data supplied to the function can be quite large, as a result of which it can be divided into separate sequentially processed blocks. For example, if it is an audio signal, then it can be buffered by the operating system, if it is data from an external device, then they can come in portions over the communication line. And also the data can be processed through the buffer and in the application itself, since the volume of possible data is not known in advance. In this case, the working buffer is allocated a certain fixed length, for example, so that they fit into a cache of some level and then all the data passes through this buffer in batches. In all such cases, the delay line is very useful. It helps to very simply “glue” data into one continuous stream in such a way that there is no edge effect of splitting data into blocks.

IPP API

Many years of experience using the IPP library revealed that it is necessary to modify the FIR filter API to meet the following requirements:

• it would be possible to process the vector in sequential blocks;
• there would be no hidden memory allocation;
• vector processing in different threads would be supported;
• In-place mode was acceptable, i.e. the input vector is simultaneously the output.

In order to fulfill all these requirements simultaneously, the concepts of “input” and “output” delay lines were introduced, after which the API began to look as follows.

This API follows the standard scheme used in IPP. First, using the ippsFIRSRGetSize function, the memory size is requested for the function context and the working buffer. Next, the ippsFIRSRInit function is called , into which the filter coefficients are supplied. This function initializes the internal data tables in the pSpec structure, accelerating the operation of the ippsFIRSR processing function . The content of this structure does not change during the operation of the function, which is reflected in its name Spec, therefore, it can be used simultaneously by several threads for more efficient use of memory. The pBuf parameter is the working and modifiable buffer of the function, therefore, each working buffer must be allocated for each thread.

The suffix SR means single rate, and is used for uniformity with MR (multi rate) filters, the description of which can be a whole separate article. The numIters parameter is also taken from MR filters and in our case means simply the length of the vector.
The parameter pSrc points to the beginning of the processed block x [0].
Now let’s look at the meaning of the pDlySrc and pDlyDst parameters.


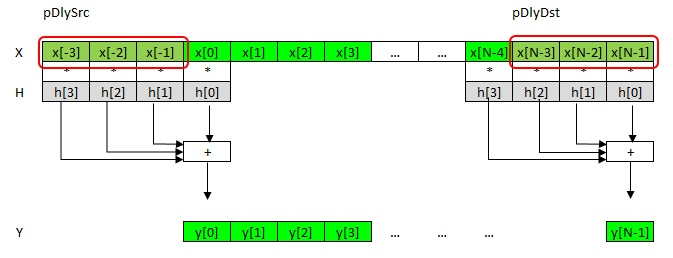
Fig. 3. “Input” and “Output” delay lines

As mentioned earlier, the need for x [-3], x [-2], x [-1] comes from the convolution formula. These elements are called the “input delay line” pDlySrc. And samples x [N-3], x [N-2], x [N-1] is the “tail” of the processed vector, ie last K-1 items. They are called the pDlyDst “output delay line.” For the next block, they will respectively be the input line and so on.
The input delay line pDlySrc can point to k-1 samples to the left of x [0], to some other buffer, or equal to NULL. In the case of NULL, it is assumed that all elements of the input delay line are 0. This is convenient for the initial block when there is no data yet.
The pDlyDst address records the “tail” of the block, i.e. k-1 of the last samples. If the value is NULL, then nothing is written.

Such a mechanism of two delay lines allows parallel processing of the vector, even in the case of in-place mode, i.e. when the vector is overwritten. To do this, it is enough to first copy the “tails” of the blocks into separate buffers and submit them as an input line to each stream. An example of the code used in the article is given at the end with a single listing.

An example of using Lowpass IPP FIR filter.

Consider, for example, how to use the IPP FIR filter in order to leave only the low-frequency component of the signal.
To generate the original unfiltered signal, we will use the special Jaehne IPP function that implements the formula
pDst [n] = magn * sin ((0.5πn2) / len), 0 ≤ n <len
This function is a workhorse on which many IPP functions are tested. We will write the generated signal to the simplest .csv file and draw pictures in Excel. The original signal looks as follows.


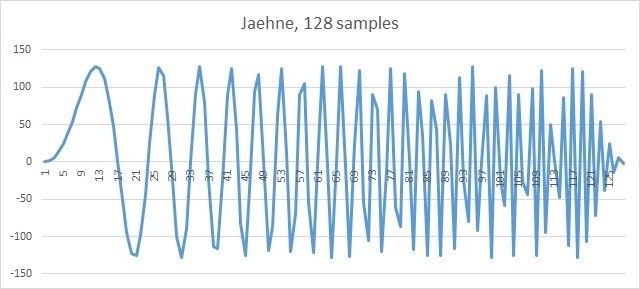
Fig. 4. 128 Samples of the Jaehne signal

. For example, consider a filter of order 31. To generate the coefficients, the IPP function ippsFIRGenLowpass_64f is used. The function calculates the coefficients only in double, so they are converted to float. See the firgenlowpass () function code in the appendix. After calling this function, the buffer size, initialization and call of the main function ippsFIRSR are calculated, and its performance is measured.
After applying the lowpass filter, the low-frequency component remained in the signal. Note that the phase is shifted, but this already follows from the properties of the FIR filters themselves and does not apply to the IPP library.


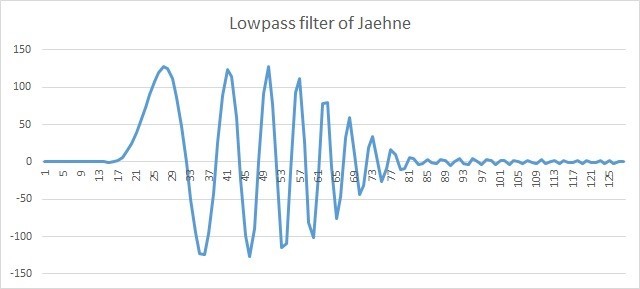
Fig. 5. 128 Samples of the Jaehne signal after the lowpass filter

In these figures, the FIR filter processes 128 samples, with 30 samples of the input delay line set to 0, indicating pDlySrc = NULL. We also do not need the output line pDlyDst = NULL.

Multithreaded Performance

The IPP library has the word performance in its name, which is put at the forefront. Therefore, we measure the performance of ippFIRSR functions on a processor with support for AVX2. After that, we implement the following multi-threaded code using OpenMP, measure it and then we will reduce the measurement results into one graph.
API FIR filter designed in such a way that the partition vector by multiple threads was simple and logical way, as shown in the figure:


Fig. 6. Splitting the original vector between flows. The

following method of splitting the vector between flows is implied, see the fir_omp function.


Consider what this code does. So, we received the next portion of the signal x [0], ..., x [N-1], which we need to process with a filter, and with it a pointer to the input and output delay lines or, in other words, the tail of the previous portion and the buffer where place the “tail” of the current portion. We want to speed up the filtering process and divide the processing of this portion into T = NTHREADS blocks, corresponding to the number of threads. To do this, we just need to correctly specify the input and output lines, and also allocate our working buffer for each stream.

For the 0th stream, the input delay line when ippsFIRSR is called is the same “tail” of the previous portion, and for all others, a pointer to the block shifted by order-1 elements is supplied as the input line. And only the last stream writes the “tail” of the portion.

The above approach implies that the resulting vector is written to a different address than the original vector, if the data is overwritten, then the delay lines should be previously copied to separate buffers.

The graph shows the performance of the single-threaded and multi-threaded versions for 4 order 31 filter threads on a processor supporting AVX2 Intel® Core (TM) i7-4770K 3.50Ghz instructions. For FIR filters, the cpMAC unit is used, i.e. the number of clock cycles per operation Multiply +
Add cpMAC = (function execution time) / (vector length * filter order)


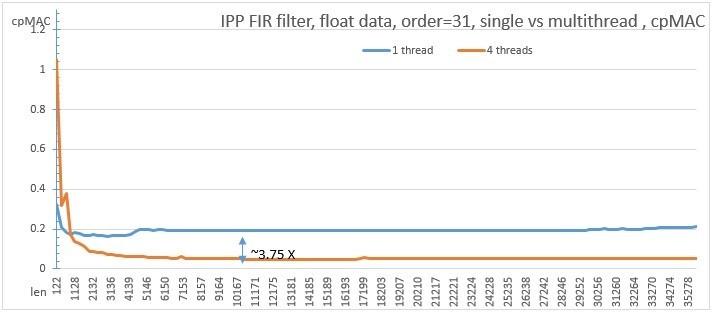
Fig. 7. Performance comparison of single-threaded and multi-threaded versions of the FIR filter

It can be seen that the function scales very well, and the multi-threaded version works approximately 3.7 times faster on sufficiently long vectors than the single-threaded version, which corresponds very well to 4 threads. The criterion for switching between single and multi-threaded versions now, with the new API, can be selected experimentally for a specific machine, unlike the previous one, where the criterion was hardwired into the code and the function was paralleled from the inside.

Comparison of direct and FFT implementations

In digital signal processing, the mutual matching of convolution and Fourier transform is widely used.
In addition to direct implementation, IPP FIR filters also have an implementation via FFT, and the resulting cpMACs sometimes exceed the theoretically possible for a given cpu and direct algorithm, as users sometimes write about in forums, rightly believing that the calculations go through FFT.

Now, in order to indicate what type of algorithm to use, one of the values ​​of the algType parameter should be used - ippAlgDirect ippAlgFFT, ippAlgAuto. The last parameter means that the function selects an algorithm according to a fixed criterion for the used cpu, and it may not always be optimal.

Consider the performance on the same CPU of a filter of different orders for the vector lengths of 1024 and 128 samples using the direct algorithm and the FFT implementation.


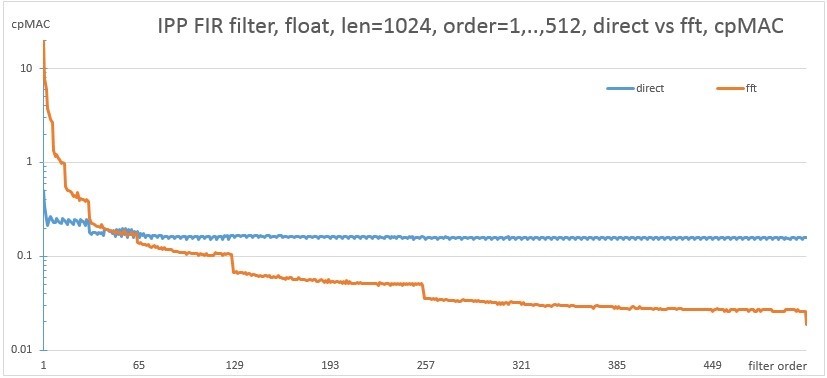
Fig. 8. Comparing the performance of direct and fft realizations for the length of the 1024 reference


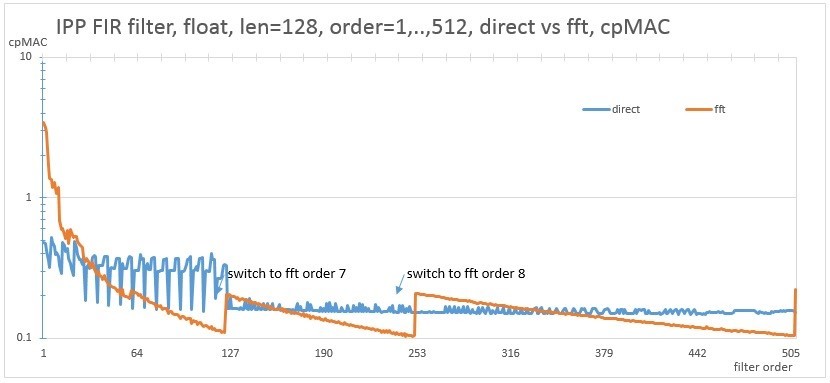
Fig. 9. Comparison of the performance of direct and fft implementations for a length of 128 samples

FFT implementation is characterized by steps. This is due to the fact that for filters of several close orders, FFT of the same order is used, and when the transition to the next order of FFT is switched on, the performance changes. To achieve maximum performance, you should use the algorithm that lies below on the graph. The proposed API allows you to implement an example that will run both versions of the algorithm to measure on a specific machine and select the best one. The picture will look something like this. In this picture, a two-dimensional space is drawn with a size of 1024x1024, where the filter order along the X axis and the vector length along the Y axis. Green color means that the fft algorithm is faster than the direct version. The characteristic straight lines at the bottom of the figure correspond to fig. 9, where the fft option is slower for a while,


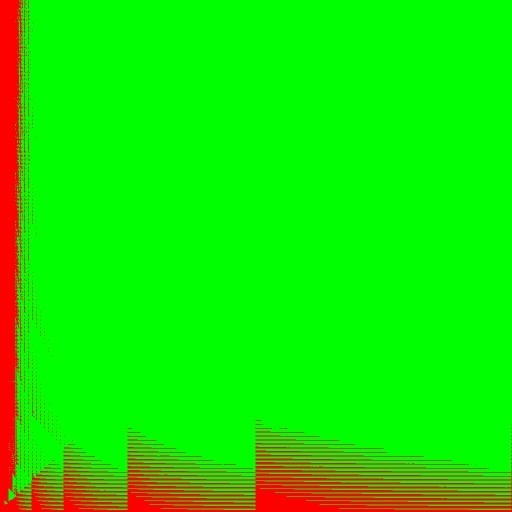
Fig. 10. Comparison of the performance of direct and fft implementation of IPP FIR float filter in filter order X vector length space of 1024 x 1024 dimension.

It can be seen that the picture is quite complex and it is not so easy to interpolate inside IPP under any platform. In addition, this pattern may vary on a particular machine. In addition to the choice between direct and fft code, you can add another dimension in the form of the number of streams and this will result in a multilayer picture. The proposed API again allows you to choose the best option for this platform option in this case.

Conclusion

The FIR filters API introduced in IPP 9.0 allows you to use them in applications even more efficiently, choosing the best option between direct and fft algorithms, as well as parallelizing each of the selected options. In addition, the IPP library is completely free and available for download from this link Intel Performance Primitives (IPP).

Application. Sample Code Measuring IPP FIR Filter Performance