How to create software for a microtomograph in 5233 man hours
I want to talk in more detail about an interesting project by Edison . The developers were tasked with writing software for a microtomograph, they did an excellent job of this, and then stuffed seeds, bolts, capacitors and moth into this tomograph. And serious uncles need this tomograph to check diamonds and not buy holey ones.
 And today is December 16, the birthday of Johann Radon , an Austrian mathematician, rector of the University of Vienna, who in 1917 introduced the integral transform of the function of many variables, akin to the Fourier transform, which is used today in all tomographs.
And today is December 16, the birthday of Johann Radon , an Austrian mathematician, rector of the University of Vienna, who in 1917 introduced the integral transform of the function of many variables, akin to the Fourier transform, which is used today in all tomographs.Johann Radon was a professor at 6 universities (and in one of them even without a department), he was president of the Austrian Mathematical Society. In Austria, he was named after him the "Institute of Computational and Applied Mathematics" and a medal.
About how the development of software for the tomograph went and what tasks were solved in the process - under the cut.
Microtomograph
Scientists from Tomsk State University have created a microtomograph. It allows you to learn the internal structure of various materials with micron accuracy. For example, diamonds.

Fig. Quality of diamonds
A tomograph can illuminate a material with a resolution of up to microns. It is 100 times thinner than a human hair. After scanning, the program creates a 3D model where you can look not only at the outside of the part, but also find out what is inside it.
Tomograph device
List of main technical characteristics of the device.
• Number of detector resolution elements: 2048 x 2018 cells with a single element size not exceeding 13.3 x 13.3 microns.
• Resolution: 13 microns.
• Dimensions: 504 x 992.5 x 1504 mm.
• Weight: 450 kg.
• Field of view: 1 mm.
• Operating wavelength range: 0.3–2.3 A.
• Positioning accuracy of electromechanical motion modules in the RMT positioning system: ± 1 μm.
• Compliance with safety requirements: GOST 12.1.030-81.
• X-ray protection: 1-3 μSv / h.

Fig. Appearance
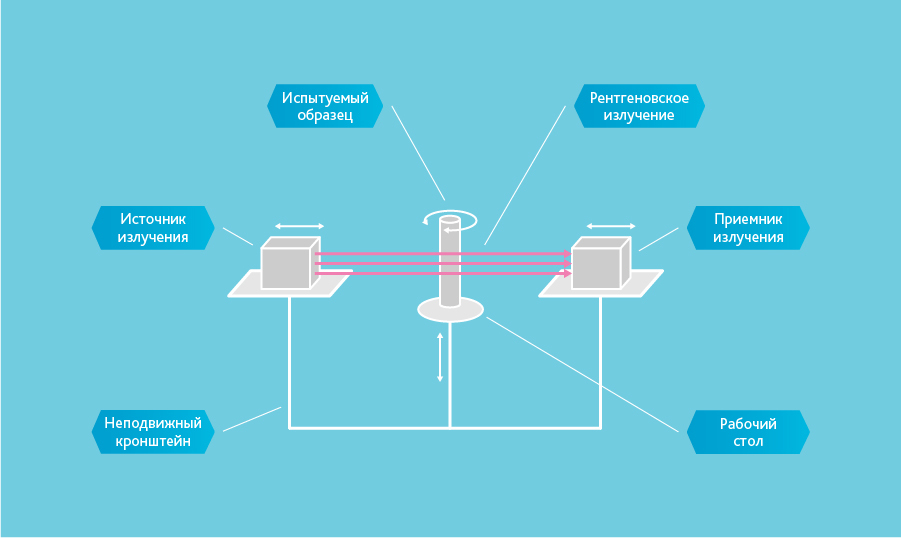
Fig. The operating principle of electro-mechanical part of

Fig. X-ray source
• Voltage: 20–160 kV.
• Current: 0–250 μA.
• Power: 10 watts.
• Focal spot diameter: 1–5 μm.

Fig. Positioning
• Rotor stroke: SEMD - 360 °, LEMD - 100 mm.
• Positioning accuracy, not less than: ± 0.5 microns.
• Rotor speed: from 0.01 to 20 mm / s.
• Power: 0.7 kW at a voltage of 70 V.

Fig. X-ray detector based on CCD array
• Sensitive CCD region: 2048 x 2048 pixels.
• Geometric pixel size: 13 x 13 microns.
• Geometric size of the sensitive area of the CCD: 26.6 x27.6 mm.
• Built-in two-speed ADC: 16 bit, 100 kHz and 16 bit 2 MHz.
• Number of detector resolution elements: 2048 x 2018 cells with a single element size not exceeding 13.3 x 13.3 microns.
• Resolution: 13 microns.
• Dimensions: 504 x 992.5 x 1504 mm.
• Weight: 450 kg.
• Field of view: 1 mm.
• Operating wavelength range: 0.3–2.3 A.
• Positioning accuracy of electromechanical motion modules in the RMT positioning system: ± 1 μm.
• Compliance with safety requirements: GOST 12.1.030-81.
• X-ray protection: 1-3 μSv / h.

Fig. Appearance

Fig. The operating principle of electro-mechanical part of

Fig. X-ray source
• Voltage: 20–160 kV.
• Current: 0–250 μA.
• Power: 10 watts.
• Focal spot diameter: 1–5 μm.

Fig. Positioning
• Rotor stroke: SEMD - 360 °, LEMD - 100 mm.
• Positioning accuracy, not less than: ± 0.5 microns.
• Rotor speed: from 0.01 to 20 mm / s.
• Power: 0.7 kW at a voltage of 70 V.

Fig. X-ray detector based on CCD array
• Sensitive CCD region: 2048 x 2048 pixels.
• Geometric pixel size: 13 x 13 microns.
• Geometric size of the sensitive area of the CCD: 26.6 x27.6 mm.
• Built-in two-speed ADC: 16 bit, 100 kHz and 16 bit 2 MHz.
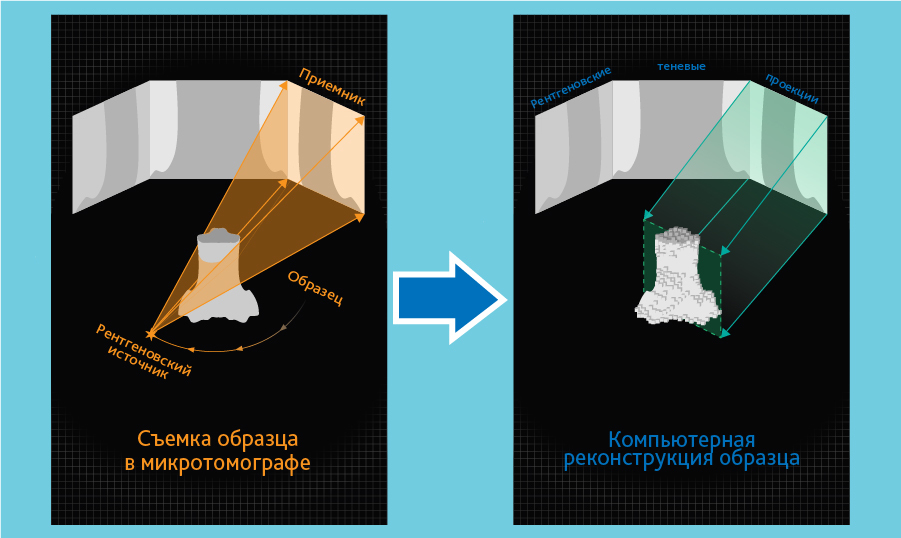
Fig. Digitization and reconstruction illustration.
Used mathematical algorithms.
- Inverse Radon Transformation.
- Marching / walking cubes.
- Gauss filter.
- Filtration / convolution, normalization of projections.
Implementation and technology.
- C ++ / Qt.
- Ubuntu, Windows.
- CUDA.
- Volumetric-voxel model rendering.
- Native 12-bit grayscale image storage format.
- Separation of the reconstruction on the client server.
- Saving voluminous data in the form of "Octo-trees".
Labor: 5233 man-hours.
Debugging was performed on raw data (projection images) obtained from the tomograph.
Algorithms
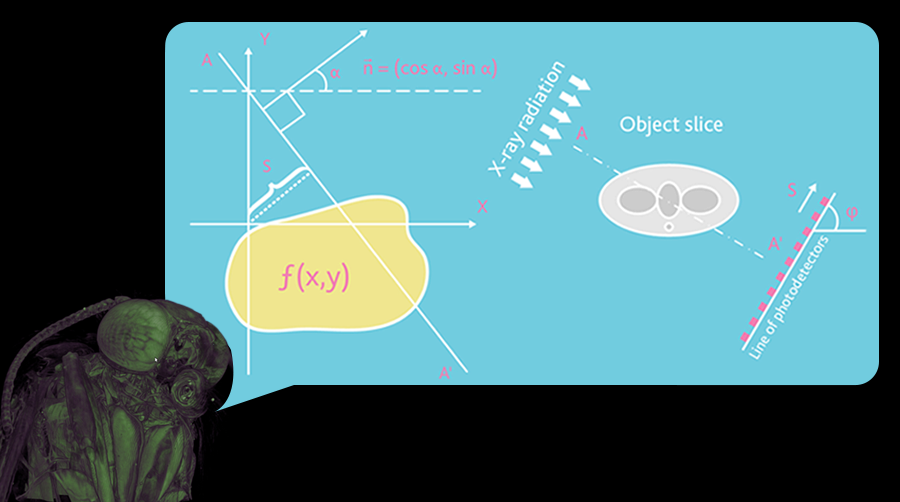
First of all, it was necessary to choose a mathematical apparatus for solving the problem. The main algorithm - the inverse Radon transform - was laid down in the statement of the problem,
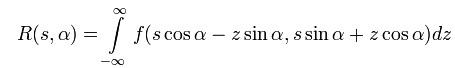
however, it was necessary to adapt it to the features of our work and use several additional, auxiliary algorithms. For example, in view of the fact that the object was illuminated by a single “light bulb”, it was necessary to adapt the formulas for the inverse Radon transform to conical rather than direct projections. The standard algorithm assumes that the object is illuminated by a beam of parallel x-rays emanating from an infinitely distant source. In reality, the source of rays is point-wise; therefore, the beam of rays has the shape of a cone. In this regard, it was required to introduce a coordinate transformation from a conical system into a rectangular one in the inverse Radon transformation algorithm.
At the first stage of calculations, preliminary filtering / convolution, normalization of projections are performed. This is necessary in order to muffle noise on the projections, and to more clearly distinguish densities.

To build 3D-models of surfaces of objects in a standard format for viewing in 3D-editors Compass, SolidWork, 3D Max Studio, the algorithm “ Marching (walking) cubes ” was used. The essence of the algorithm is that it runs through a scalar field, at each iteration it looks at 8 neighboring positions (vertices of a cube parallel to the coordinate axes) and determines the polygons needed to represent the part of the isosurface passing through this cube. Next, polygons forming a given isosurface are displayed.
A Gaussian filter in a project is understood as matrix filters for image processing using a convolution matrix. The convolution matrix is a matrix of coefficients that is “multiplied” by the value of the image pixels to obtain the desired result. The filter is used to smooth voxel data and slice projections, which, in turn, improves the quality of the generated 3D models ( Habrapost 1 , Habrapost 2 ).
Implementation and Technology
In the course of the work, a number of specialized technical solutions were also created: a library for volume-voxel model rendering; video recording during operations with the model; native format for storing images with shades of gray 12 bits deep; Saving voluminous data in the form of "Octo-trees"; polygonization algorithms of the 3D model.

Volume-voxel model rendering in the project was used to view the model with the possibility of rotation and scaling in real time. VoxelIs a three-dimensional pixel. Also, with the help of voxel rendering, the operator is provided with convenient tools for determining the viewing area with automatic increase in the level of detail and the ability to position the cutting plane at any angle in two clicks. Based on the secant plane, in the future it is possible to obtain a slice image with maximum resolution.
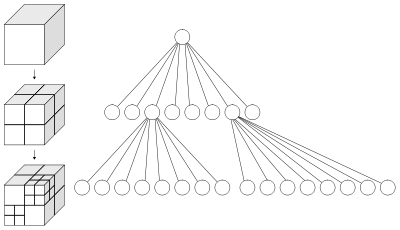 Oktoderevo(octant tree, octal tree, English octree) is a type of tree-like data structure in which each internal node has exactly eight “descendants”. Octal trees are most often used to separate three-dimensional space, recursively dividing it into eight cells. In the project, the octree allows you to display data in preview mode when there is no need for data that is not visible to the user. So, for example, volumetric rendering receives a data set for displaying with detail depending on the selected area using the octree, which provides high FPS when the entire model is visible, and at the same time an increase in detail if some smaller part of the model is selected.
Oktoderevo(octant tree, octal tree, English octree) is a type of tree-like data structure in which each internal node has exactly eight “descendants”. Octal trees are most often used to separate three-dimensional space, recursively dividing it into eight cells. In the project, the octree allows you to display data in preview mode when there is no need for data that is not visible to the user. So, for example, volumetric rendering receives a data set for displaying with detail depending on the selected area using the octree, which provides high FPS when the entire model is visible, and at the same time an increase in detail if some smaller part of the model is selected.Debugging
This was followed by the optimization stage. For one object, the tomograph produces 360 images, each with a resolution of up to 8000 * 8000. Since the volume of processed data is large, the solution of the “head-on” problem would be completely unsatisfactory. This was taken into account at the design stage, however, after receiving the first version, the algorithms had to be optimized and adapted several times. The task required that the time for creating a three-dimensional model of the microstructure not exceed 2 hours, so the optimization stage was laid down initially. When testing the first version, we were faced with the fact that using the standard projection image storage format is not suitable for the project. Input contains TIFF imageswith 16-bit grayscale coding. Such a color depth is excessive for calculations, and the processing of such images requires a lot of disk space, network channel, RAM and processor time. On the other hand, the standard 8-bit color depth was not enough for us to maintain the accuracy of the reconstruction. Therefore, a format for storing images with 12-bit color depth was developed.
The technical design involved the horizontal scaling of computing. The reconstruction of the 3D model, that is, the main computational task, was divided into small task packages, which the central software module distributed over the network of servers in the cluster. The servers used CUDA technology, allowing you to use the computing power of GPUs for calculations. The time required to calculate one model is reduced in proportion to the number of servers in the cluster, since the computational tasks are perfectly parallelized, and all servers are 100% loaded.

The CUDA architecture is applicable not only for high-performance graphics computing, but also for various scientific calculations using nVidia graphics cards. Scientists and researchers make extensive use of CUDA in various fields, including astrophysics, computational biology and chemistry, fluid dynamics modeling, electromagnetic interactions, computed tomography, seismic analysis, and much more. CUDA has the ability to connect to applications using OpenGL and Direct3D. CUDA is cross-platform software for operating systems such as Linux, Mac OS X and Windows.
In our project, CUDA is used for the main process - reconstruction of volume data from projections. Since the GPUs have a specialized set of instructions, the reconstruction calculations fit well on the graphics cards through the CUDA technology. On the CPU, this task is solved longer both at the development stage and at the execution stage.

Cards supported by our software:
- Nvidia Tesla K80 24GB (scientific);
- EVGA GeForce GTX TITAN X 12GB (Gaming).
The task provided that the software should work in Microsoft Windows XP / Vista / 7, Linux. In this regard, the cross-platform solution was laid down initially. C ++ / Qt was chosen as the development language, which allowed us to have a single source code and build software for different OSs.
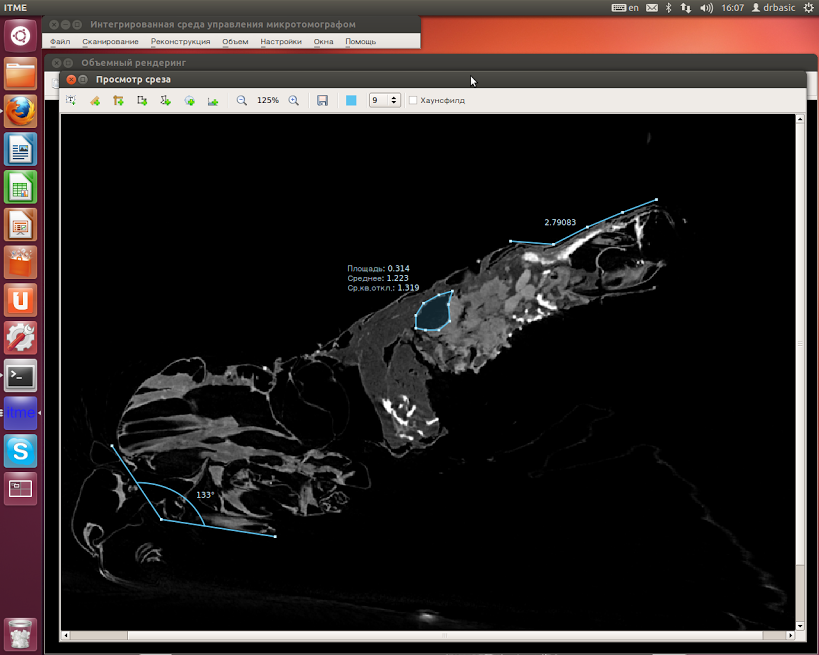
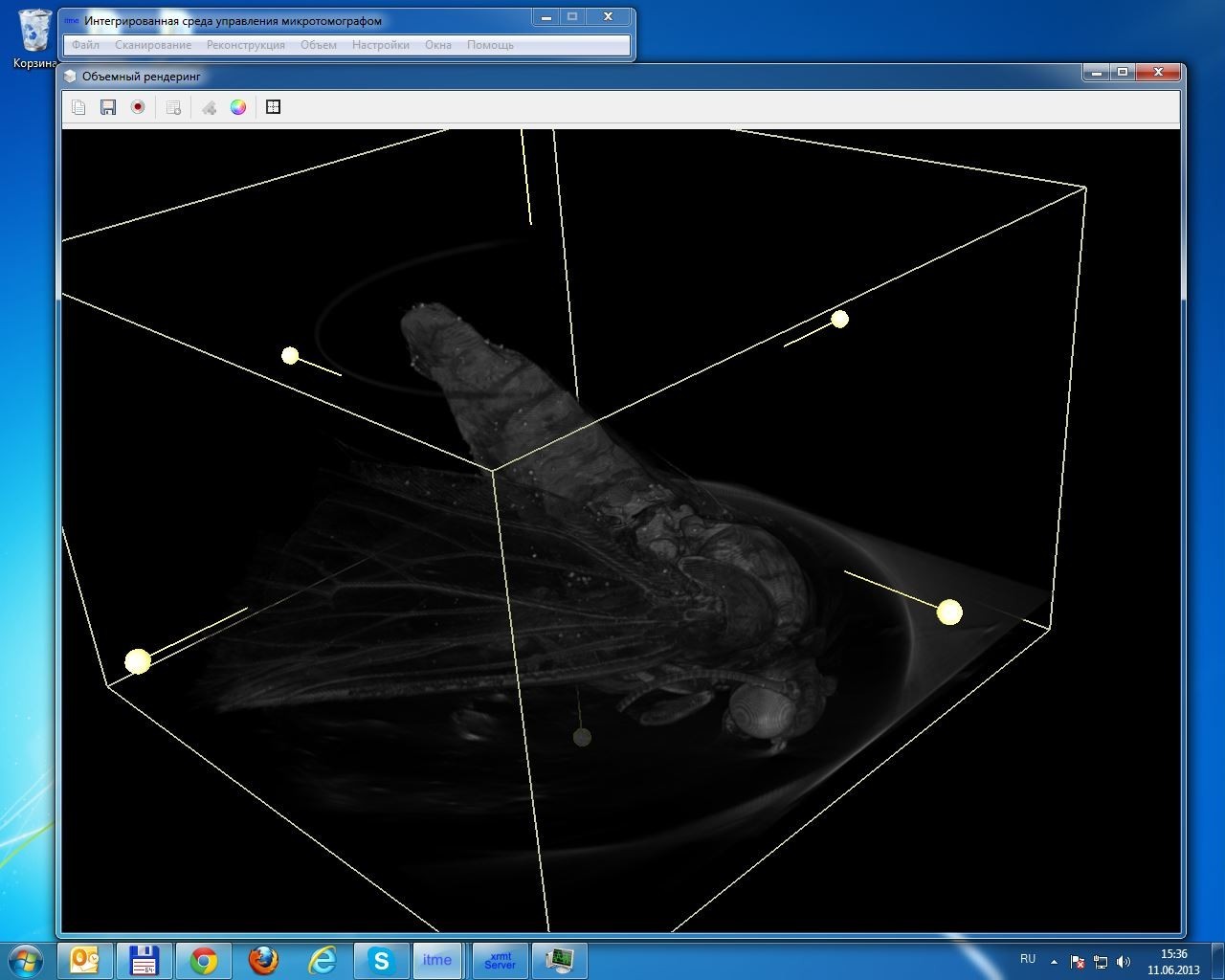
Video

More projects:
How to create software for the
SDK microtomograph for 5233 man-hours to implement support for e-books in the FB2 format
Managing access to electronic documents. From DefView to Vivaldi We
integrate two video surveillance systems: Axxon Next and SureView.
More about the development of software for X-ray tomography
Scope: how to monitor billions of kilowatt hours.
Developing a simple plug-in for JIRA to work with the database.
DevOps: firmware builder for network devices on Debian for 1008 hours
Auto-update Windows service through AWS for the poor
